主辅拦截器协同制导方法研究

邵长兴，孙 玄，张 迪，刘 慧，张佳梁

(上海机电工程研究所，上海 201109)

0 引言

随着现代导弹技术的发展，导弹的突防能力已越来越强。任何一次拦截失误都有可能带来毁灭性的打击，这就对防空导弹和拦截器提出了更高要求。为提升拦截器的杀伤力并降低成本，可利用主辅拦截器同时对目标进行拦截。主拦截器与辅拦截器采用时间协同的制导律，进行协同制导，在同一时刻实现对目标的拦截摧毁，以增强杀伤力[1]。

目前，国内外对协同控制的研究较多，但主要集中在无人机(UAV)和机器人领域[2-7]。随着现代防御技术的发展，为增强导弹的杀伤力和突防能力，导弹的协同制导和饱和攻击也逐渐成为研究热点。文献[8]针对反舰导弹在面对舰艇配备的近程防御武器系统(CIWS)时突防能力较弱的问题，提出了一种利用多角度、同时刻饱和式攻击进行突防的策略，通过控制导弹依次经过预先设定的期望通过的位置点，使导弹按预设轨道命中目标，最终实现一种同时具有攻击角度和攻击时间约束的协同制导律。文献[9-12]以反舰导弹为研究对象，基于最优控制理论，设计了可对导弹攻击时间进行控制的制导律。该制导律通过设定期望攻击时间，引入1个时间误差反馈，控制弹道轨迹弯曲以实现协同攻击。但文献未给出设定期望攻击时间的具体方法和工程可用的时间误差计算方法。文献[13-15]介绍了一种基于协调变量的协同控制方法，针对需进行协同控制的多弹协同，提出了协调变量和协调函数的概念，协同控制的单位间需实现信息的共享与交换，但此法对飞行器间的通信提出了较高要求，在工程应用中尚有一定困难。综合上述文献可以发现，国内外对多拦截器拦截高速目标的协同制导方法的研究较为缺乏，相关研究多针对UAV和反舰导弹，此类拦截器按照预设的弹道轨迹飞行，仅能攻击固定目标或舰船类低速目标。高速飞行的拦截器一般采用固体发动机，速度不可任意调节，不能停止、盘旋和倒退，且目标多为高速飞行器，无法采用类似反舰导弹预设弹道轨迹的方法进行协同攻击。

本文针对上述拦截器的特点，通过预先设定期望命中时间，将时间协同问题转换为时变系统、末值型性能指标和末端受约束(即命中时间约束)的最优控制问题，可采用极小值原理进行求解，同时采用基于比例导引律的时间协同制导律设计，使导弹无需按照预设的弹道轨迹飞行，具备自主飞行拦截高速目标的能力。

1 拦截器-目标相对运动模型

设计协同制导律前，需先建立拦截器与目标的相对运动模型，本文以1枚拦截器为例。为便于分析，设拦截器I与目标T在同一平面内，所建模型如图1所示。

图1 拦截器与目标初始位置关系Fig.1 Initial relationship between interceptor and target

其中：目标T静止于点(Xf,Yf)；v为拦截器速度且速率保持恒定；θ为拦截器速度向量与基准线间的夹角；拦截器法向加速度指令a由2个不同的指令组成，一个是用于减小脱靶量的反馈指令aB，另一个是用于调节拦截时间的附加指令aF。则拦截器的运动学方程可表示为

(1)

式中：X，Y分别为拦截器的横、纵向坐标；t为拦截器飞行时间。初始和终端条件分别为

(2)

由建立的运动模型可知，时间协同制导实质为具有终端时间(tp)限制条件的导引问题，该问题可转为线性化系统的最优控制问题。其状态方程为

(3)

(4)

式中：θ为小量；x为独立参数。

线性化模型建立后，在此模型上可用最优控制理论中的极小值原理设计制导律。

2 拦截时间可控的协同制导律

根据研究对象的特点，可设计一种拦截时间可控的协同制导律(ITCG)。

根据最优控制原理中的极小值原理，由式(4)可写出代价函数

(5)

式中：x0，xf分别为独立参数x的初值和终值。考虑拦截器平均速度v不可控，取其为常数，拦截时间约束可表示为关于拦截器飞行航程的约束，即

(6)

同样可转化为

(7)

该线性最优化问题可用极小值法解析求解。该问题的哈密尔顿函数为

(8)

式中：λy，λθ为协状态。针对本文控制无约束的情况，哈密尔顿函数H对最优控制解取驻值，对应条件为∂H/∂u=0。

根据最优性条件可得最优制导指令

uB=-λθ=-vy(xf-x)

(9)

式中：vy为满足终端条件的连续参数。代入式(4)可得

(10)

因此，初始时刻的反馈制导指令可写为uF的函数，即

(11)

则连续时间反馈控制律为

(12)

将式(12)代入式(4)，由积分运算求得用x多项式表示的航向角θ(x)为

θ(η)=αη2+βη+γ，η∈[x,xf]

(13)

(14)

求解式(14)，可得附加指令

(15)

(16)

联合式(12)和式(16)可得满足ITCG的制导指令表达式为

(17)

上述公式推导皆基于无量纲化的参数，形成式(17)的无量纲控制指令。将式(17)的ITCG在时域内物理意义下的表达式转换为

a=aB+aF=

(18)

在控制时间误差不大时，式(18)的平方根部分可近似为泰勒展开的第1项，式(18)可表示为

(19)

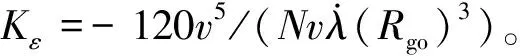
3 仿真与分析

对多枚拦截器攻击固定目标进行仿真，验证取相同期望命中时间时的协同状况。设：每枚拦截器速度恒为300 m/s；拦截器I1初始位置为(-9 093 m，5 250 m)，航向角为-35°；拦截器I2初始位置为(-6 364 m，-6 364 m)，航向角为75°；拦截器I3初始位置为(-2 070 m，-7 727 m)，航向角为105°；拦截器I4初始位置为(4 750 m，-8 277 m)，航向角为105°；目标静止于(0 m，0 m)。4枚拦截器在初始时刻与目标的相对距离近似，采用PNG制导时时间相差较小，满足采用ITCG的条件。设定期望命中时间为36 s(略大于比例导引估得的命中时间最大值)。

仿真所得4枚拦截器分别用PNG和ITCG制导攻击固定目标的弹道轨迹如图2所示。图中：实线表示拦截器采用PNG制导时的弹道轨迹，所用攻击时间分别为35.026，30.844，27.416，31.885 s；虚线表示拦截器采用ITCG制导时的弹道轨迹，4枚拦截器所用攻击时间均为36 s。

图2 4枚拦截器弹道轨迹Fig.2 Ballistic trajectories of 4 interceptors

仿真所得4枚拦截器在2种制导律下的弹目相对距离分别如图3,4所示。由图3可知，4枚拦截器在PNG制导下所用时间都不相同。由图4可知，4枚拦截器在36 s时的弹目相对距离趋于零，实现了协同制导。

图3 4枚拦截器比例制导时弹目相对距离Fig.3 Distance between interceptor and target of 4 interceptors by PNG

图4 4枚拦截器协同制导时弹目相对距离Fig.4 Distance between interceptor and target of 4 interceptors by ITCG

对3枚拦截器拦截运动目标进行仿真。设：每枚拦截器速度均为600 m/s，并保持速率不变；拦截器I1的初始位置为(0 m，0 m)，航向角为65°；拦截器I2的初始位置为(10 km，0 m)，航向角为50°；拦截器I3的初始位置为(-5 km，10 km)，航向角为55°；目标初始位置为(59 km，77.140 km)，初始速度为730 m/s，航向角为-145°，在重力加速度g=9.81 m/s2作用下运动。

计算得最大预测拦截时间为63.9 s，则设置期望拦截时间为65 s(略大于由比例导引估得的拦截时间最大值)，此时对应的拦截点选为(20 km，30 km)。导弹在初始时刻与目标相距98 km，采用ITCG制导，当相距30 km时，切换为PNG制导。

仿真所得4枚拦截器分别用PNG和ITCG制导拦截运动目标的弹道轨迹如图5所示。其中：实线表示目标弹道轨迹；虚线表示拦截器采用PNG制导时的弹道轨迹，拦截时间分别为63.559，60.783，61.987 s；点线表示拦截器采用ITCG制导时的弹道轨迹，期望拦截时间为65 s，实际仿真拦截时间分别为64.905，64.915，65.046 s，满足设计要求。

图5 3枚拦截器弹道轨迹Fig.5 Ballistic trajectories of 3 interceptors

仿真所得3枚拦截器在2种制导律下的弹目相对距离分别如图6，7所示。由图6可知，3枚拦截器在PNG制导下所用时间都不相同。由图7可知，3枚拦截器在65 s时的弹目相对距离趋于零，实现了协同制导。

图6 3枚拦截器比例制导弹目相对距离Fig.6 Distance between interceptor and target of 3 interceptors by PNG

图7 3枚拦截器协同制导弹目相对距离Fig.7 Distance between interceptor and target of 3 interceptors by ITCG

通过上述仿真可知，采用ITCG制导可实现对固定目标与高速飞行目标的时间协同制导，该方法在工程应用中具备一定的可实施性。在设计过程中，可假定拦截器速度恒定不变，并通过预计命中位置预估期望飞行时间，而在工程应用中，拦截器飞行速度实时变化，目标也可能进行机动，因此如何准确预测目标运动轨迹与命中位置将是后续的研究重点。

4 结束语

本文对主辅拦截器协同制导方法进行了研究。针对主辅拦截器的拦截特点，通过设定期望时间，在比例导引律的基础上引入1个包含时间误差的修正项。根据相对运动模型，将时间协同制导问题视作一个有终端时间限制条件的导引问题，最终将其转为线性化系统的最优控制问题，用最优控制中的极小值原理设计了协同制导律，并对多枚拦截器分别攻击静止目标和运动目标进行了仿真。结果表明：设计的基于比例导引律的时间协同制导律可实现对目标的协同攻击，无需预设弹道轨迹，通过设定期望拦截时间可对高速飞行目标进行时间协同制导，未来可应用于防空导弹对高价值目标的协同拦截。主辅拦截器协同制导是一个非常新颖且极为复杂的问题，本文仅研究了一些理想状态下的问题，后续将针对机动目标的拦截时间和拦截点的准确预测进行进一步研究。

[1] 彭锐晖, 王国宏, 陈士举, 等. 两弹协同定位的可行性研究[J]. 系统仿真学报, 2006, 18(5): 1118-1122.

[2] CHANDLER P R, PACHTER M, RASMUSSEN S. UAV cooperative control[C]// Proceedings of the American Control Conference. [S. l.: s. n.], 2001: 50-55.

[3] CHOI J, KIM Y. Fuel efficient three dimensional controller for leader-follower UAV formation flight[C]// International Conference on Control, Automation and Systems. [S. l.: s. n.], 2007: 806-811.

[4] 周明, 孙树栋, 彭炎午. 基于遗传算法的多机器人系统集中协调式路径规划[J]. 航空学报, 2000, 21(2): 146-149.

[5] 秦世引, 潘宇雄, 苏善伟. 小型无人机编队飞行的控制律设计与仿真[J]. 智能系统学报, 2009, 4(3): 218-225.

[6] 樊琼剑, 杨忠, 方挺, 等. 多无人机协同编队飞行控制的研究现状[J]. 航空学报, 2009, 30(4): 683-691.

[7] STILWELL D J, BISHOP B E. Platoons of underwater vehicles: communication, feedback, and decentralized control [J]. IEEE Control Systems Magazine, 2000, 20(6): 45-52.

[8] JUNG B, KIM Y. Guidance laws for anti-ship missiles using impact angle and impact time [C]//AIAA Guidance, Navigation, and Control Conference and Exhibit. Colorado: AIAA, 2006: 1-13.

[9] JEON I S, LEE J I, TAHK M J. Impact-time-control guidance law for anti-ship missiles[J]. IEEE Transactions on Control Systems Technology, 2006, 14(2): 260-266.

[10] KIM K B, KIM M J, KWON W H. Receding horizon guidance laws with no information on the time-to-go [J]. Journal of Guidance, Control, and Dynamics, 2000, 23(2): 193-199.

[11] TAHK M J, RYOO C K, CHO H J. Recursive time-to-go estimation for homing guidance missiles[J]. IEEE Transactions on Aerospace and Electronic Systems, 2002, 38(1): 13-24.

[12] BEN-ASHER J Z, YAESH I. Optimal guidance with reduced sensitivity to time-to-go estimation errors[J]. Journal of Guidance, Control, and Dynamics, 1997, 20(1): 158-163.

[13] MCLAIN T W, BEARD R W. Coordination variables, coordination functions, and cooperative timing missions [J]. Journal of Guidance, Control, and Dynamics, 2005, 28(1): 150-161.

[14] BEARD R W, MCLAIN T W, NELSON D B, et al. Decentralized cooperative aerial surveillance using fixed-wing miniature UAVs [J]. Proceedings of the IEEE, 2006, 94(7): 1306-1324.

[15] 赵世钰, 周锐. 基于协调变量的多导弹协同制导[J]. 航空学报, 2008, 29(6): 1605-1611.