信息视角下基于异质信念的股票波动性价值研究
张 普,陈 亮,曹启龙
常州大学 商学院,江苏 常州 213164
引言
股票价格波动是证券市场上永恒的话题。长期以来,人们普遍认为波动是资产价格不确定性的具体表现,是市场参与者面对的风险的主要来源。然而,事实却是,波动虽然导致损失,但同时也为市场参与者带来了收益的机会,股票价格的波动同时具有风险和价值的双重属性,它们相生相伴,并在一定条件下相互转化。但无论表现为风险还是价值,波动都应是股票价格构成中不可或缺的影响因素,并且这种微妙关系产生的根本原因应来源于市场参与者的异质信念或偏好[1]。
进一步,除了固有的个性和能力等因素外,市场参与者异质信念或偏好的形成及其对市场和投资标的的认知在很大程度上取决于信息的力量。对于金融市场中的信息冲击问题,有效市场假说已经进行了经典的诠释,大量的后续研究也充分证实了信息在市场中的作用。信息,尤其是私人信息对股票价格产生的影响不容质疑,信息与市场参与者信念及偏好的形成,进而与股票价格波动息息相关。
由此,本研究在信息视角下,基于无套利原理和期权博弈思想建立理论模型,以风险和价值的双重属性分析股票价格波动以及由此产生的股票波动性价值,探讨其在不完全或不对称信息条件下的表现形式。
1 相关研究评述
1.1 股票波动性价值
关于波动性的研究数量颇丰,但大多均未将其作为股票价格形成的独立影响因素,概括地说,从价值角度进行的波动性研究大体可分为起源、发展、突破3个阶段。
1.1.1 起源阶段
关于波动性价值的研究起源于现代金融学对股票流动性价值的探索,在早期波动仅仅被视为构成股票流动性价值的一个因素。
LONGSTAFF[2]的流动性期权理论是有关股票流动性价值的著名成果之一。该研究认为,交易受限的股票产生折价的主要原因在于流动性的缺失,而决定折价程度的主要因素则是收益波动率。基于投资者完美择时能力假设,流动性期权理论还得出了流动性折价的最大值,但却在实证中发现现实的折价程度接近甚至超过了这个最大值[3]。其后,LONGSTAFF[4]、吴卫星等[5]、KOZIOL et al.[6]和梁朝晖等[7]分别基于美国存信股票、中国国有股、债券和封闭式基金对该理论进行扩展和应用,但遗憾的是,都没能对这一现象做出合理的解释。
因此,本研究有理由相信,流动性价值并非交易受限股票产生折价的唯一原因,波动作为股票价格的独立影响因素开始进入人们的视线。
1.1.2 发展阶段
波动可能是股票价格过程中相对独立的影响因素,但表现为风险。
随着关于金融市场微观结构的研究日益深入,人们发现股票波动性与流动性之间存在不完全相关关系[8],且在一定程度上互为因果[9]。研究发现在资产定价的横截面检验中,波动因子是显著的,并且模型误差优于CAPM[10];无论市场波动是长期的还是短期的,它们的影响都是负的[11];在存在“跳跃”的日内高频数据中,连续性的波动成分也能对收益具有解释能力[12];中国A股市场中,波动率风险也是一个显著的横截面定价因子且其风险价格为负[13];基于中国香港市场的研究也得出了类似的结论[14]。至此,波动开始作为股票价格过程中相对独立的影响因素进入人们的视线,但尚未涉及波动对股票价格行为的影响机制问题。
1.1.3 突破阶段
在这个阶段,基于异质交易行为及有限理性的波动性研究开始出现,从机制上初步证实波动性不仅表现为风险,也可能表现为价值。
实证研究表明,市场参与者的异质信念会影响股票价格的波动,且随着信念差异程度的扩大,股票价格的波动会加剧[15]。异质信念对波动性的影响取决于市场参与者的自信和乐观程度[16],如过度自信的市场参与者就会产生“噪音”,进而提高风险资产的波动水平[17]。张宗新等[18]构建数理模型论证由于信念调整导致投资者情绪变化,进而引致市场异常波动的路径;朱宏泉等[19]以未预期交易量作为异质信念的代理指标,证实异质信念与股票收益波动存在联系;虞文微等[20]从特质波动率角度论证了上述关系。
在理论上,基于内在价值不变假设,已证实股票上市过程中可能存在正的波动性价值,而以市场交易者异质信念为背景,在股票价格和波动率序列连续、市场信息完全且对称、市场交易者完全理性条件下,也可证实股票价格波动既可能表现为风险,也可能表现为价值[21]。由此,初步实现了股票波动性价值研究理论的突破。
1.2 信息不对称与股票波动
目前,尚未见到关于信息与股票波动性价值之间关系的研究,相关研究多从实证角度专注于信息不对称程度对股票波动水平的影响。由于信息不对称程度难以直接测度,所以已有研究通常从信息透明度、机构投资者持股和证券分析师关注3个角度间接实现。
信息透明度角度,JIN et al.[22]利用全球40个市场的数据,得出信息不透明程度越强,信息不对称水平越高,股票的波动性越大的结论;LEE[23]利用美国市场的日内数据,证实信息流冲击及其透明度与股价的“跳跃”显著相关;刘志东等[24]利用中国股票市场数据,进一步分析上市公司的经营公告、财务报告及证券分析师基于上述信息的股评等3类不同信息的披露对股价波动的影响,发现不同类别的信息对股价异常波动的影响力不同,且经营公告的影响力最大。此外,基于会计稳健性视角,王冲等[25]实证研究表明,信息不透明程度越高的企业,其股价暴跌风险越大;而文凤华等[26]从行为金融的角度描述了股市信息流对收益波动性的影响。
机构投资者持股角度,在机构投资者持股水平究竟会对信息不对称产生何种影响的问题上学界尚有分歧。一方面,大部分研究认为机构投资者将通过降低市场的信息不对称水平实现平抑波动的作用,CALLEN et al.[27]和AN et al.[28]认为机构投资者能够有效地监督管理者抽取公司现金流的行为,这降低了公司的特质风险。同时,机构投资者的监管作用减弱了管理者对坏消息的囤积,从而降低了股价未来的暴跌风险。宋小保[29]、许年行等[30]和程天笑等[31]利用中国上市公司数据,分别从企业盈利能力、羊群行为和合格境外机构投资者的视角证实机构投资者持股能降低市场波动。另一方面,基于英美股市的研究认为,机构投资者羊群行为有可能推高信息不对称程度进而增大市场波动水平[32];基于中国股市的研究中,邢治斌等[33]发现机构投资者出于既追逐收益又适度避险的动机,往往偏好持有适度波动的股票,因而加剧市场波动;代昀昊等[34]的研究证实机构投资者能够凭借私有信息推高当前股价。但他们最终均得出信息不对称程度与股票波动水平正相关的结论。
证券分析师关注角度,研究较为广泛。基于日内数据的研究发现证券分析师是市场最重要的信息披露途径之一,因而将降低市场波动[35],基于长期增长预测的研究得到类似的结论[36]。此外,SIMON et al.[37]关于明星分析师的研究和肖土盛等[38]关于股价崩盘风险中证券分析师的中介作用的讨论,虽然最终结论不尽相同,但在关于信息不对称程度与股票波动性关系的问题上都得出了二者呈正相关关系的结论。
1.3 评述
综上所述,关于股票波动性价值的研究已经取得了一定的突破,但由于已有模型的假设条件较强,因此难以有效反映现实世界中股票波动性价值的具体表现形式。至于信息不对称与股票波动之间的关系,已有研究虽然在实证中得出了基本一致的结论,但却鲜少能从理论角度对这一现象做出合理的解释,而对信息不对称程度与股票波动性价值之间的关系更是甚少涉及。
因此,基于已有的波动性价值研究,从信息视角入手,建立更符合市场实际情况和需求的股票波动性价值模型,分析股票波动性价值的具体表现形式,进一步明确波动作为独立影响因素对资产价格的影响,无疑是资产定价领域中非常有意义的研究方向之一。
2 模型构建
H1市场参与者异质性。根据交易动机,可将市场参与者分为价值型参与者和市场型参与者。价值型参与者更关注股票的内在价值和上市公司的长期业绩增长,并以获取公司未来发展的长期收益为目的;市场型参与者更希望通过短期内的低买高卖获取利润。
H2市场参与者是价格接受者,市场无摩擦。
H3理性市场参与者E和参与者F根据自身需求独立进行决策,二者均不一定掌握完全信息,且不了解对方的信息状态。
根据H1和H2,构造资产组合复制正常交易中的A股票。令t∈[0,T],T为模型设定的用于测算股票波动性价值的总时长,t为总时长中的任意时点。t=0时,A的市场价格为S,有与A对应的可流动但价格无波动的股票A0,其价格为S0。当t∈(0,T]时,A0只能以S买入或卖出。
市场参与者E面临的两个策略如下:
策略一:
①买入一份A0,其价格为S0,当t∈(0,T]时,只能以价格S卖出;
②买入一份或有请求权C,其价格为PC,执行价格为St,即E可以在任意t∈(0,T],以St卖出一份A0,其中,St为t时刻A的市场价格;
③卖出一份或有请求权D,其价格为PD,执行价格为S,D的持有者F是与E分属不同类别的市场参与者,他可以在任意t∈(0,T],以执行价格S向E卖出一份A;
④C和D中只能有一个行权,即当其中一个行权时,另一个便作废。
策略二:直接以价格S买入一份A。
探讨S0如何取值才能令E认为这两种策略无差异。
根据无套利原理,有
S=S0+PC-PD
(1)
由此定义信息视角下的股票波动性价值为V,有
(2)
可见,股票波动性价值是指波动在股票价格构成中的贡献率,其大小和方向取决于或有请求权C和D的价格,直观上,其绝对值越大,表明波动对股票价格的影响越大。对市场参与者E而言, C可能带来价值和收益,D却代表着风险和损失,因此令C为波动收益性请求权,D为波动损失性请求权。
对比相关期权的收益曲线,可以将C看做一个美式下敲出看涨期权,执行价格为标的股票A的初始价格,敲出价格为D行权时标的股票A的价格SDt;而将D看做一个美式上敲出看跌期权,执行价格也为标的股票A的初始价格,敲出价格为C行权时标的股票A的价格SCt。由此,进一步令C为波动收益性期权,D为波动损失性期权。
由H3可知,理性市场参与者E和参与者F根据自身需求独立进行决策,因此模型中关于障碍期权C和D敲出时点的判断可简化为对D和C行权时间的计算,即先行权者获取收益,且另一方期权敲出。同时,由于E和F均不一定掌握完全信息,因此当期权C和D的最优停时出现时,他们将根据自身的信息掌握情况做出是否行权的决策。
至此,(1)式中两个美式障碍期权的博弈已经简化为不完全且不对称信息条件下两个美式期权最优停时的判断,以及对双方市场参与者是否行权决策的比较。
3 模型求解
美式期权的求解往往要运用数值方法,如有限差分法、二叉树法、蒙特卡罗法等。经过比较,本研究采用LONGSTAFF et al.[39]提出并经GLASSERMAN et al.[40]优化的最小二乘蒙特卡罗模拟法,对波动收益性期权C和波动损失性期权D的最优停时进行判断,并根据理性市场参与者E和参与者F的信息掌握情况,设计二者之间的博弈过程,以体现信息水平对股票波动性价值的影响。
不难发现,判断只掌握着不完全信息的E和F是否会在模型计算出的最优停时上行权,是信息视角下股票波动性价值模型求解的关键所在。遗憾的是,这是一个不确定性问题,如果具体到每一位市场参与者,具体到每一条模拟的股票价格路径,是无法给出答案的。为此,本研究采用博弈论中处理不完全信息博弈的方法,运用海萨尼转换将不完全信息博弈问题转化为完全但不完美信息博弈问题,进而判断市场参与者的行权情况。
具体求解步骤如下。
(1)运用蒙特卡罗技术获得A的价格路径,共M条。

(3)对任何一条路径i,运用最小二乘蒙特卡罗模拟求出C和D的最优停时,分别记为Cti和Dti,再求出最优停时时点对应的现金流,分别记为CFCi和CFDi。
(4)基于海萨尼转换的思想,设定一个外生的虚拟参与人——“自然”,进而建立信息矩阵,并由其决定在每条路径上E和F是否会在前面计算出来的最优停时行权。
按均匀分布赋予“自然”一定的概率,并据此建立信息矩阵,记为Ram,表示不同路径上市场参与者的信息掌握程度。令Rami,j∈[0,1],若Rami,j=1,表示该路径上的市场参与者掌握完全信息;若Rami,j=0,则表示该路径上的市场参与者不掌握任何信息。事实上,现实中市场交易者的信息掌握程度往往介于上述两种情况之间,即大多数情况下,Rami,j是一个介于0~1之间的数。因此,本研究赋予“自然”的概率即可表示市场参与者的信息水平。Rami,j越接近于1,市场参与者的信息越完全;Rami,j越接近于0,市场参与者掌握的信息越少,越不完全。

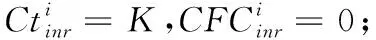
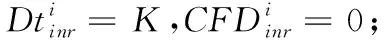

(7)基于各自所处的时点,将经过调整的现金流折现,求得该路径上C和D的价格。
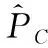
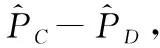
4 信息视角下的股票波动性价值特征
H4A股票的价格St遵循几何布朗运动,即
dSt=(r-q)Stdt+σStdB
(3)
其中,r为无风险收益率,q为连续现金红利率,σ为波动率,r、q、σ均为常数,B为一个标准维纳过程,有
(4)
运用Matlab软件对模型进行求解。其中,离散化时点数K和股票价格路径数M的设定兼顾了效率和精度,由于中国股票市场年度交易日平均为252个,以一年中每天10次交易机会计算,令K=2 520;根据经验,模拟的股票价格路径数以万条为数量级即可满足求解精度要求,同时为使Matlab生成的路径更具随机性,将路径数设为不能被100整除的数,因此令M=10 101。
4.1 现金红利率对股票波动性价值的影响
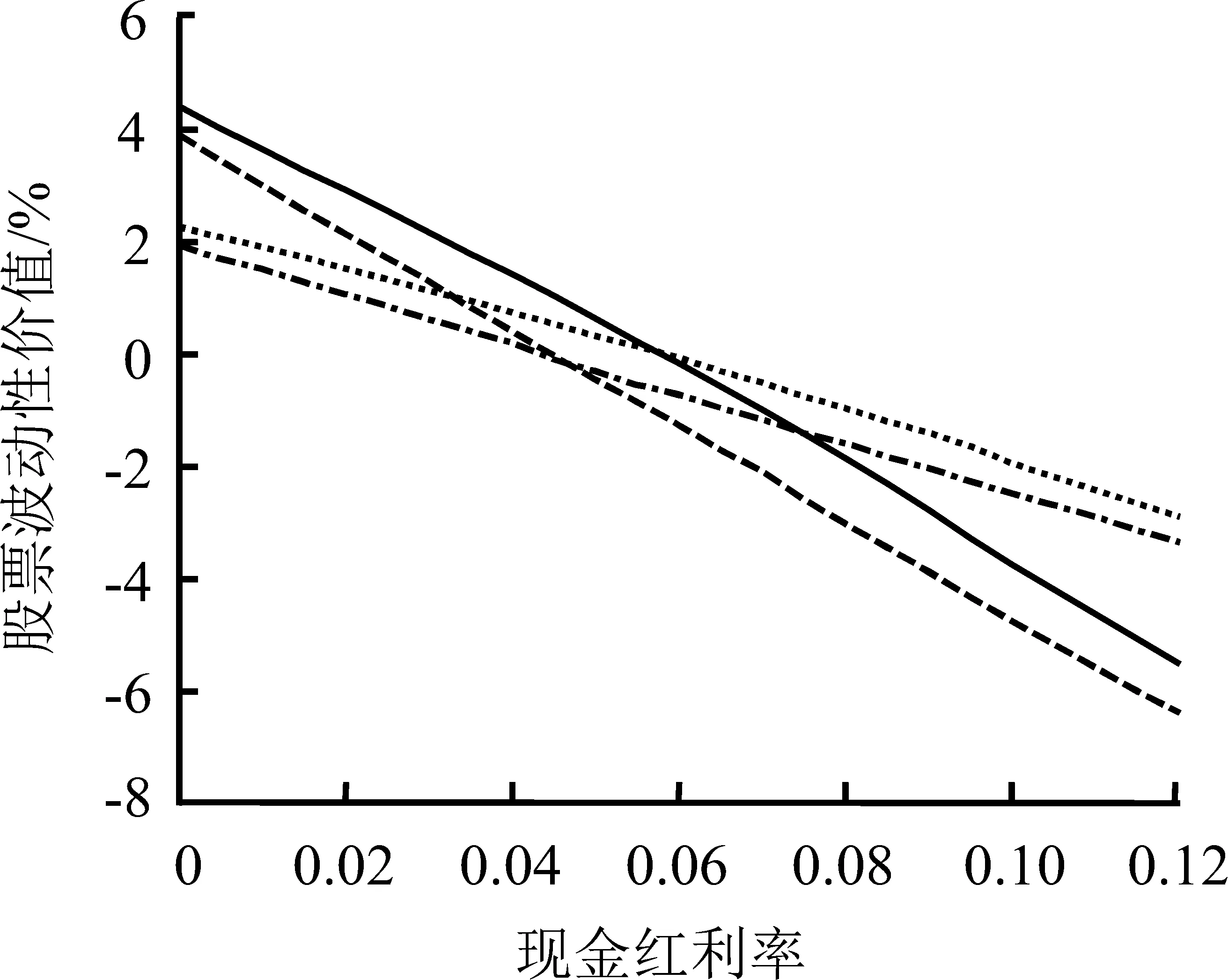
令S=10,r=0.06,图1给出信息视角下连续现金红利率对股票波动性价值的影响,图1(a)~(d)分别给出在信息完全且对称、信息不完全但对称、信息不完全且不对称-波动收益性期权信息占优、信息不完全且不对称-波动损失性期权信息占优的条件下,当其他参数分别满足T=1和σ=0.10、T=1和σ=0.70、T=0.50和σ=0.10、T=0.50和σ=0.70时,现金红利率在区间[0,0.12]间变动对股票波动性价值的影响。q=0,表示没有红利发放;q=0.06,表示现金红利率等于无风险收益率,持有成本为零;q>0.06,表示股票的持有成本为负。
从图1看,无论信息条件如何,股票波动性价值与现金红利率水平呈负相关关系。当红利为零或水平比较低时,股票波动性价值多为正值。虽然在有些特定的信息条件下,即便现金红利率为零,股票波动性价值仍然为负,但并没有改变其随现金红利率水平上升而下降的总体趋势。
4.1.1 信息不完全但对称条件下的股票波动性价值特征
假设市场参与者E和F掌握的信息是对称的,且假设“自然”为50%,即相关市场参与者的信息掌握程度为50%。这样设定既能反映信息不完全对股票波动性价值的影响,又能保证信息完全与信息不完全在子图曲线上的差异足够明显。
(a)信息完全且对称

(b)信息不完全但对称
(c)信息不完全且不对称-波动收益性期权信息占优
(d)信息不完全且不对称-波动损失性期权信息占优
图1信息视角下连续现金红利率对股票波动性价值的影响
Figure1InfluenceofContinuousCashDividendRatesonStocks′VolatilityValueBasedonInformationalPerspective
图1(b)反映了信息不完全但对称条件下的股票波动性价值特征。
(1)从图中曲线的相对位置看,图1(b)与图1(a)没有显著差异,表明信息不完全并不会改变股票波动性价值与现金红利率水平之间的总体关系。
(2)期限越长,股票波动性价值随红利水平变化的斜率越大;波动率水平越高,股票波动性价值越低。由此可知,一方面,长期投资者对红利水平的变化更加敏感,这与已有研究及市场实际交易中人们的认知吻合,即长线投资者更关心股票的内在价值,更倾向为价值型市场交易者;另一方面,其他条件不变时,股票波动性价值与波动率水平成反向变动关系,即高波动率往往对应更低的股票波动性价值,表明市场参与者并不欢迎高波动,这一结论也与大多数市场参与者是风险厌恶的观点一致。
(3)信息不完全条件下,无论波动性表现为价值还是风险,其绝对值都较信息完全条件下有所下降,且下降幅度与本研究设定的“自然”选择概率相当。究其原因,是由于市场参与者在信息不完全的情况下,无法把握最佳的交易时点,进而导致交易业绩下降。由此又一次证明,信息在市场交易中具有举足轻重的作用。
(4)信息不完全条件下,当波动率水平较高时,股票波动性价值的波动较大,表现为对应的曲线不够平滑;而波动率水平较低时,在平滑度上与信息完全条件下的股票波动性价值曲线没有显著差异。这种现象表明,越是在高波动的市场上,信息的作用就越明显,拥有信息优势可能带来的收益会更多,而处于信息劣势时可能蒙受的损失也就越大。
(5)股票波动性价值趋于零,即波动给市场参与者带来的双方面的影响基本持平的时点,一般对应于现金红利率水平与无风险收益率基本持平的位置,即对应于q=0.06的位置,且股票波动性价值下降至零的时点早于现金红利率水平与无风险收益率持平,即持有成本降为零的时点,这一现象可以由行为金融学中关于损失厌恶的观点解释。
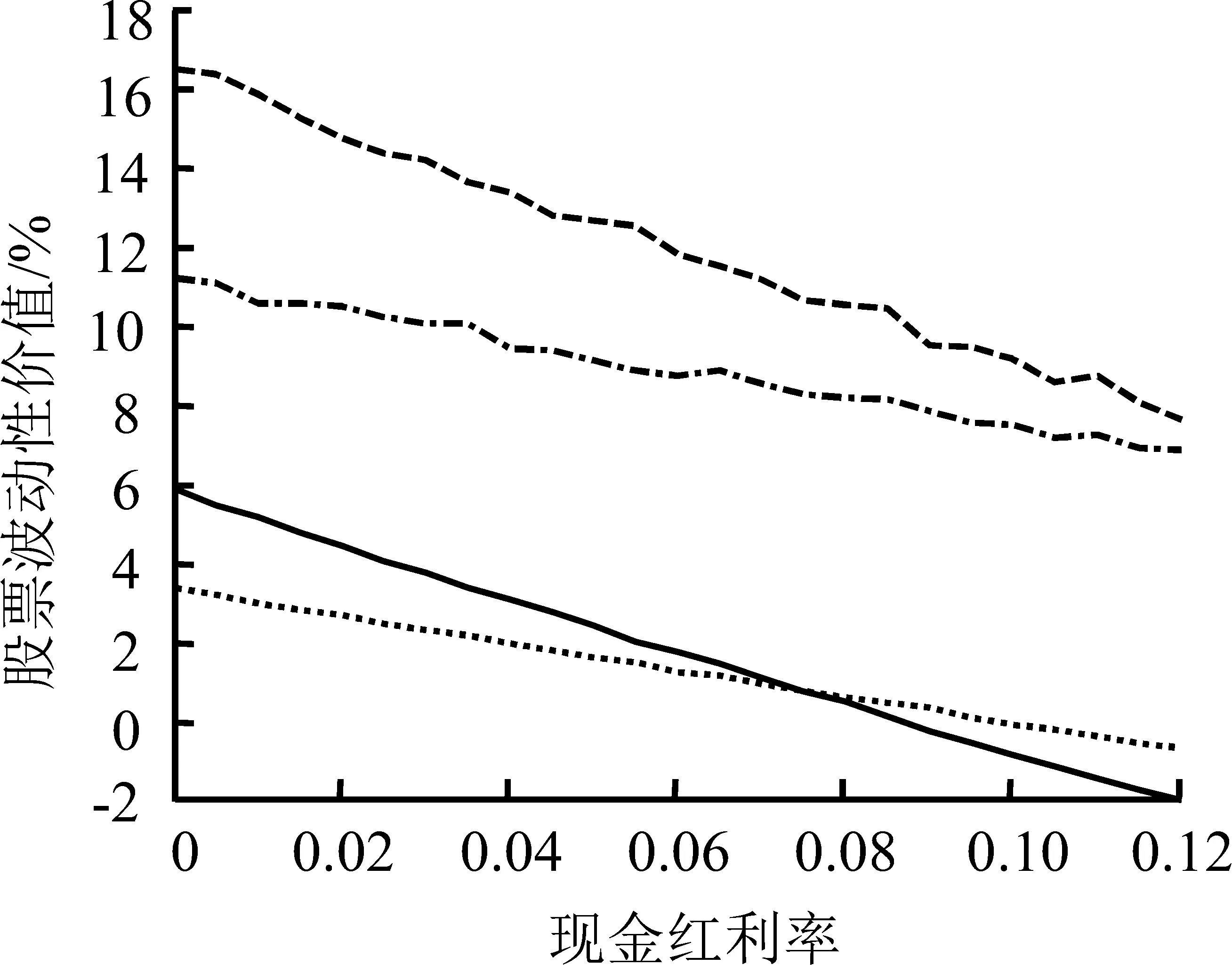
4.1.2 信息不完全且不对称条件下的股票波动性价值特征
图1(c)和图1(d)反映的是信息不完全且不对称条件下的股票波动性价值特征,图1(c)中波动收益性期权处于信息优势,图1(d)中波动损失性期权处于信息优势。为了适当减少计算量,提高运算速度,求解过程中将处于信息优势的一方设定为完全信息,而将处于信息劣势的一方的“自然”选择概率设定为50%。除上文关于图1(a)和图1(b)描述的总体趋势外,此时的股票波动性价值还具有如下特征。
(1)从图中曲线的相对位置看,图1(c)和图1(d)基本类似,但与图1(a)和图1(b)之间却存在显著差异。表明真正对股票波动性价值产生决定性影响的并非是信息的不完全,而是信息的不对称。
(2)信息优势对股票波动性价值的大小具有决定性的影响,同时能明显放大波动率水平对波动性价值的作用。
对比图1(c)与图1(a),可见其他因素不变条件下,当波动收益性期权具有信息优势时,股票波动性价值显著提升,以T=1和σ=0.10为例,图1(a)代表的信息完全且对称条件下,股票波动性价值区间为(-6%,5%),图1(c)代表的波动收益性期权信息占优条件下,股票波动性价值变化区间为(-2%,6%),可见,信息优势为市场参与者赢得了机会,他们对股价波动的理解和把握也更加有效,并且这种机会更多地表现在对损失的规避上:股票波动性价值的最小值由接近-6%上升到-2%,波动性风险大幅下降;股票波动性价值的最大值由不足5%上升到约6%,仅在一定程度上升。因此,可以认为,信息优势对波动性风险的规避效率更高。
高波动与低波动之间股票波动性价值的差距显著扩大,仍以T=1为例,图1(a)中,低波动(σ=0.10)和高波动(σ=0.70)的两条股票波动性价值曲线差距不明显,图1(b)中,虽然高波动导致股票波动性价值的波动幅度加大,但高、低波动的两条股票波动性价值曲线之间的相对差距仍不明显。然而在图1(c)中,高波动的股票波动性价值曲线已远离低波动曲线,可知当信息不对称时,信息优势或劣势将放大波动率带来的影响。换句话说,拥有信息优势的市场参与者可以利用股票价格的波动谋求更高的收益,波动率水平越高,这种潜在的可能收益就越大,因而这些投资者应该更偏好较高的波动率水平。
对比图1(a)与图1(d)的纵坐标和4条曲线间的相对位置,发现当波动损失性期权处于信息优势时,波动性风险也得到了充分的放大,即当对手处于信息优势时,波动将在很大程度上放大风险。
(3)投资期限越长,波动率增加带来的股票波动性价值变化越明显。
图1(c)和图1(d)中,T=1表示期限为一年的投资,视为长期投资;T=0.5表示半年期投资,视为短期投资。可见,低波动(σ=0.10)和高波动(σ=0.70)之间股票波动性价值曲线的差距不同,高波动(σ=0.70)的两条曲线间的纵向距离分别在10%左右,低波动(σ=0.10)的两条曲线间的纵向距离分别只有8%,长期投资的差距更明显。而在图1(a)和图1(b)中这种差距并不显著。由此可以认为,投资期限越长,随波动率水平的上升,信息优势或劣势为市场参与者带来的收益或损失越大。
(4)信息不对称将改变股票波动性价值趋于零时对应的现金红利率水平,促使市场参与者交易动机的转化。
图1(a)和图1(b)中,股票波动性价值的取值由正值转为负值,即波动在股票价格行为中的作用由价值转化为风险,基本是在现金红利率水平逐渐增加直至与无风险收益率基本持平,即持有成本不断降低直至接近于零时发生的。然而,信息不对称条件下,股票波动性价值和风险的转化却并非如此,而是根据市场参与者信息优势的方向不同,向不同的方向发生偏离。图1(c)中,有利的信息使股票波动性价值在多数情况下为正值,股票波动性价值与风险的转换点也处于持有成本为负(即现金红利率水平高于无风险收益率)的区域,高波动(σ=0.70)情况下表现更为明显。图1(d)中,不利的信息使股票波动性价值在多数情况下为负值,股票波动性价值与风险的转换点明显处于持有成本为正(即现金红利率水平低于无风险收益率)的区域,高波动(σ=0.70)情况下的表现更为明显。
不仅如此,总体上,图1(a)和图1(b)中,高波动的股票波动性价值曲线始终处于低波动的股票波动性价值曲线下方,图1(c)高波动带来的股票波动性价值远远高于相应低波动水平的股票波动性价值。这样的结果表明,当拥有信息优势时,市场参与者不仅可能偏好较高的波动率水平,且这种偏好有可能改变人们对波动的根本态度,使之由一个价值型的市场参与者转变成一个市场型的参与者。从图1(c)的曲线中可以清楚地发现,只要波动率水平足够高,不论是否存在现金红利,更不论现金红利率水平的高低,股票波动性价值可以始终保持为正。
由此可知,价值型市场参与者和市场型市场参与者的划分界限并非绝对,信息不对称将在很大程度上改变市场参与者的立场和波动偏好类型,波动率水平本身将进一步放大这种改变,导致拥有信息优势的一方掌握的股票波动性价值迅速上升,甚至远远高于股票连续现金红利率的水平,此时即便是曾经厌恶波动的价值型市场参与者也将乐于享受波动性为其带来的丰厚利益。
4.2 波动率水平对股票波动性价值的影响
4.2.1 不同信息条件下波动率水平与股票波动性价值的关系
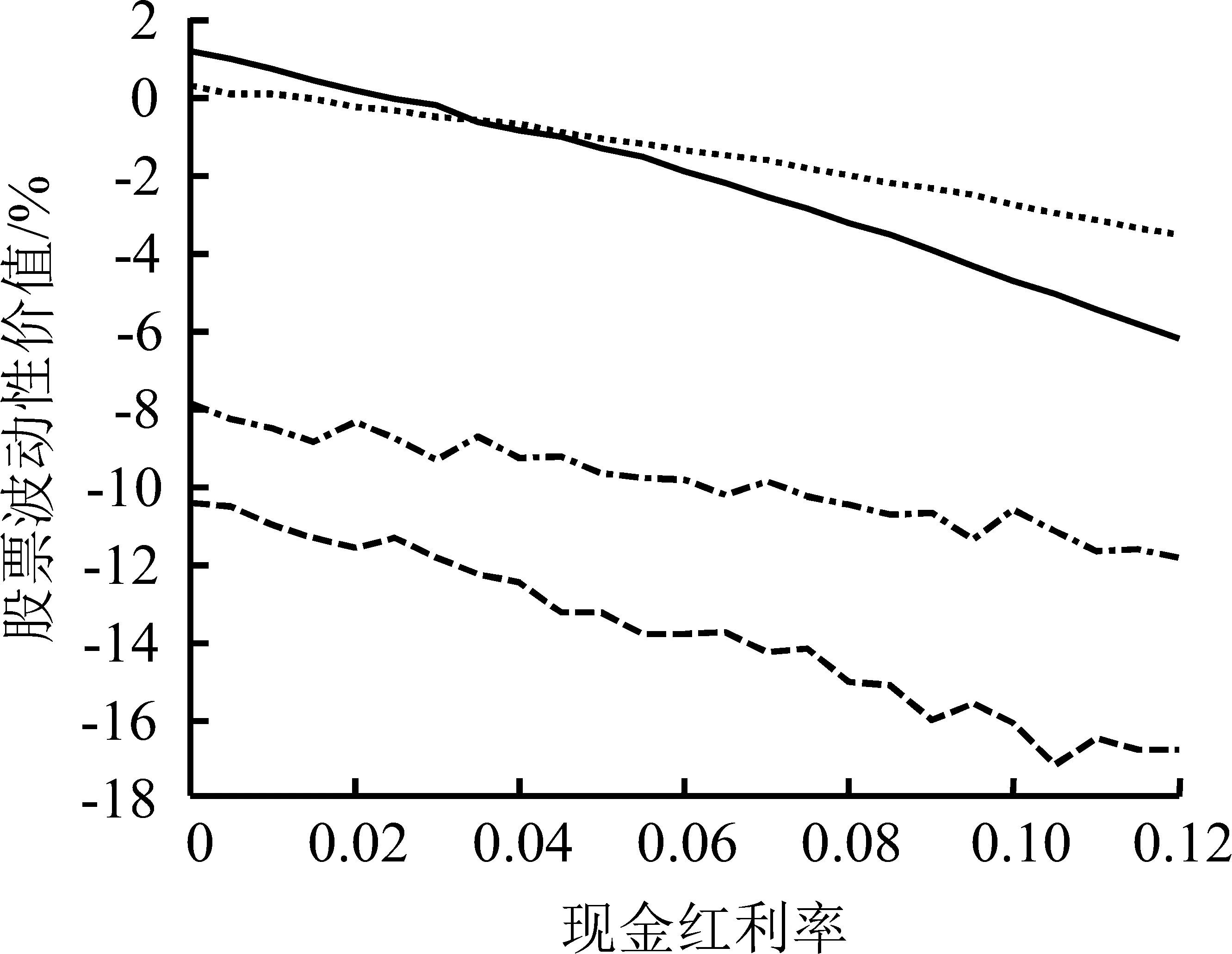
令S=10,r=0.06,T=1,连续红利率分别取0、0.06、0.12和0.18时,图2给出不同信息条件下波动率水平与股票波动性价值的关系。
图2(a)和图2(b)分别给出信息完全且对称和信息不完全但对称条件下股票波动性价值的特征。①图2(b)的纵坐标取值范围小于图2(a),再次证实在其他因素不变的条件下,如果所有市场参与者都处于同等程度的信息匮乏状态,他们可能获得的由股票价格波动带来的预期收益或承担的预期风险都会有所下降。②信息不完全但对称条件下的股票波动性价值随波动率水平变化的一般趋势没有发生明显变化,表明信息不完全并非影响股票波动性价值总体趋势的主要原因。③所有现金红利率水平下,股票波动性价值曲线都出现了较大程度的波动,尤其在波动率水平较高时,波动更加明显,表明对称的不完全信息会影响股票波动性价值的体现,降低市场效率。即当市场上的博弈双方都主要由噪音交易者构成时,信息的匮乏导致决策正确的比例下降,进而影响波动性作用的充分发挥。
(a)信息完全且对称
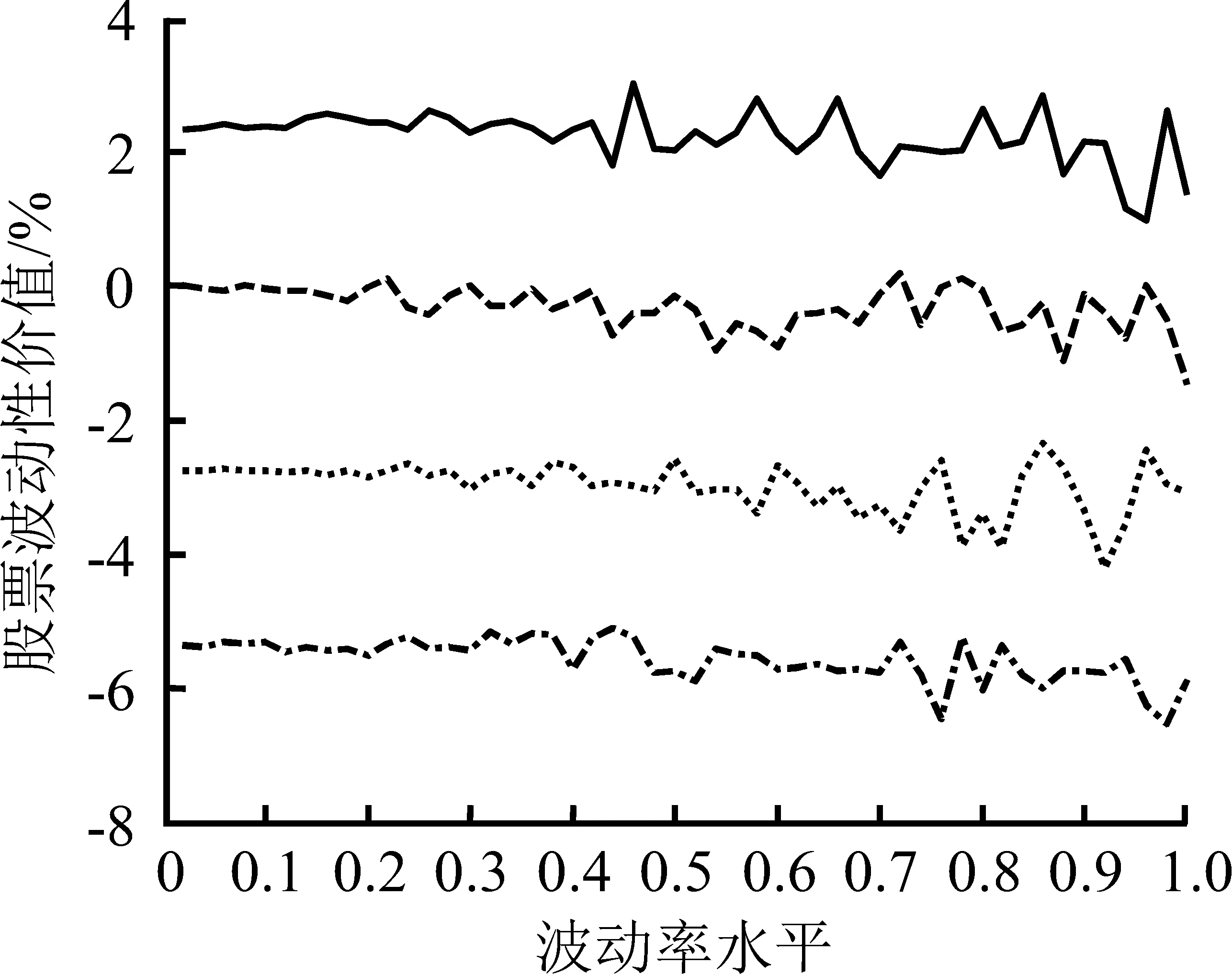
(b)信息不完全但对称
(c)信息不完全且不对称-波动收益性期权信息占优
(d)信息不完全且不对称-波动损失性期权信息占优
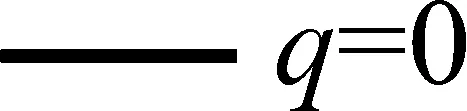
图2不同信息条件下波动率水平与股票波动性价值的关系
Figure2RelationshipbetweenVolatilityRateandStocks′VolatilityValueinDifferentConditionsofInformation
图2(c)和图2(d)给出信息不完全且不对称条件下的股票波动性价值曲线。一方面,前文得出的股票波动性价值总体上随现金红利率水平的提高而下降的结论仍然成立,表明信息不完全且不对称不会影响市场参与者对股票波动性价值与现金红利率水平之间关系的基本判断,即使由于信息水平的影响,市场参与者对股票波动性价值的方向的预期已经改变,现金红利率水平对价值型参与者和市场型参与者的划分和决策行为的作用仍然不变。另一方面,无论股票波动性价值的取值是正还是负 ,信息优势都将在很大程度上放大股票波动性价值或风险。图2(c)和图2(d)中,股票波动性价值曲线的斜率的绝对值显著大于图2(a)和图2(b),且信息优势方将在波动性期权的博弈过程中占据明显的优势。由此可知,当市场上知情交易者和噪音交易者共存时,知情交易者可以根据自己的立场得到更多的获利机会和预期收益;同时,信息优势的存在,使市场参与者对股票的波动率水平更加敏感,表现为股票波动性价值曲线的斜率的绝对值更大,单位波动率水平变化导致的股票波动性价值变化更大。
4.2.2 不同现金红利率条件下信息不完全或不对称的效应分析
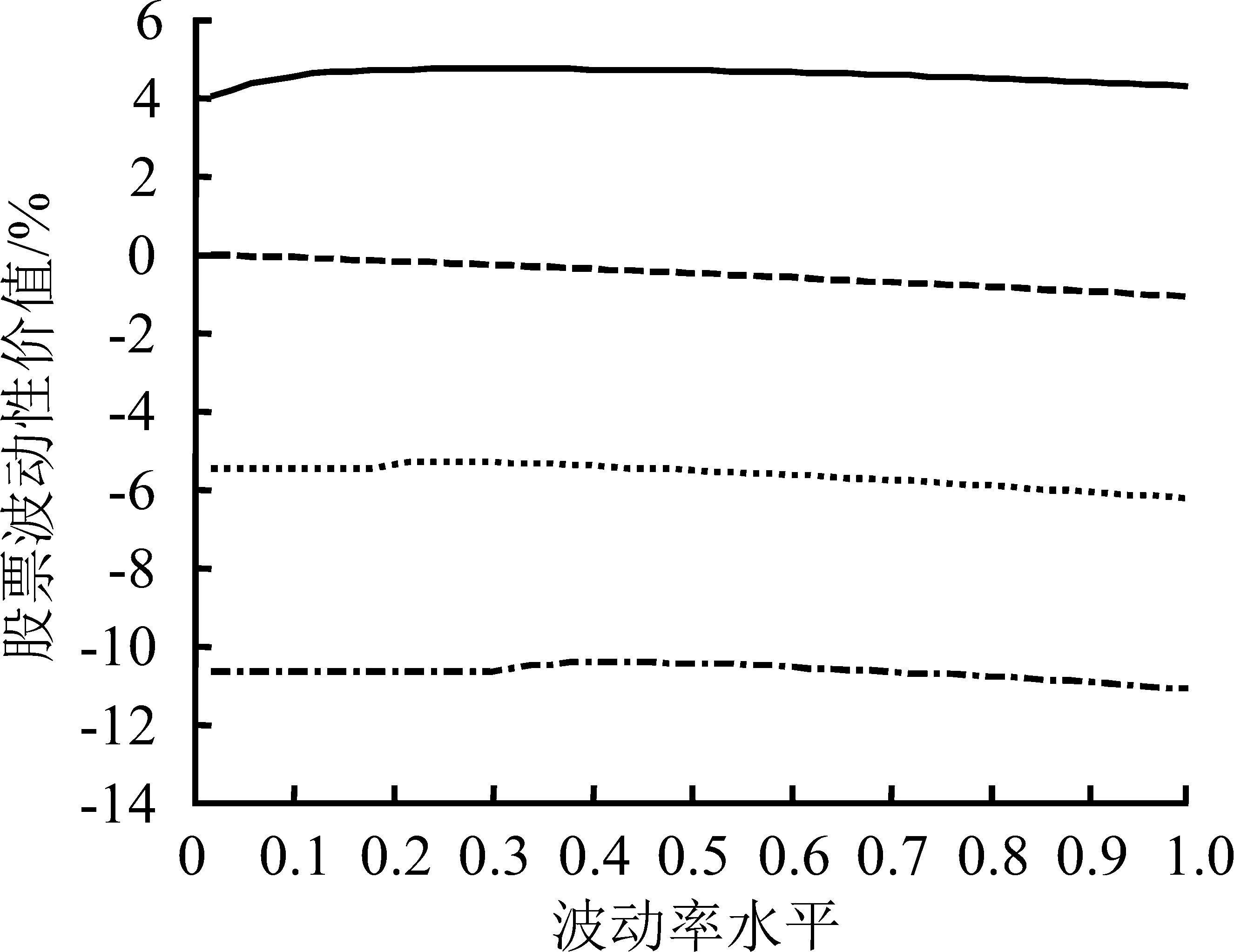
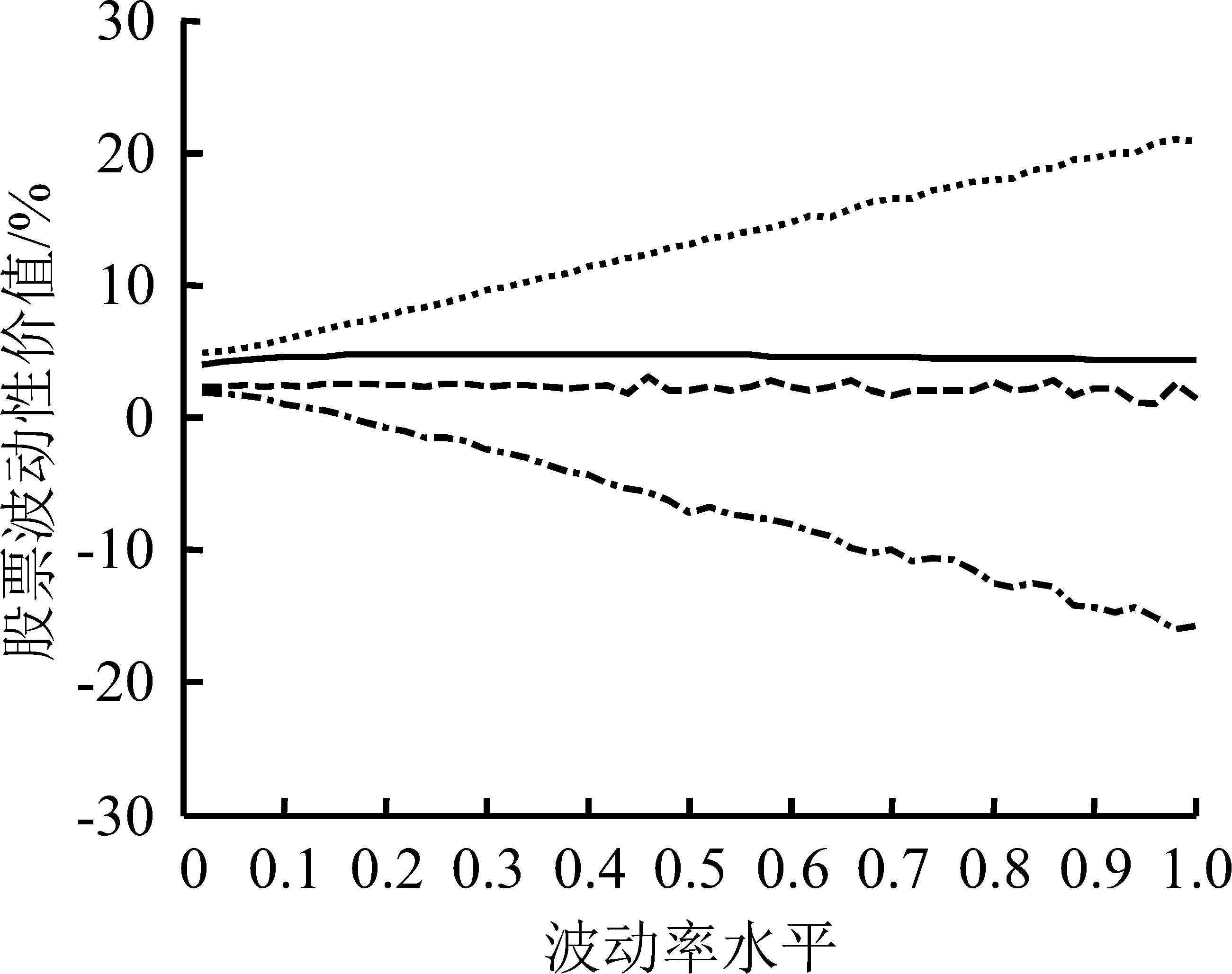
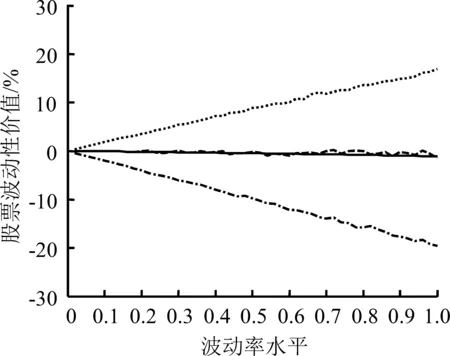
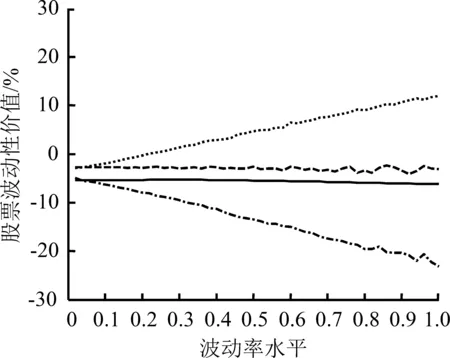
图3给出不同现金红利率水平下信息不完全或不对称的效应分析。令S=10,T=1,r=0.06,图3(a)、(b)和(c)的现金红利率分别为0、0.06和0.12,图3中曲线为股票波动性价值在不同信息条件下随波动率变化的情况。
值得注意的是,如果信息是对称的,那么股票波动性价值曲线在信息完全且对称与信息不完全但对称之间仍然存在差异。图3(a)中,信息完全且对称的股票波动性价值曲线位于信息不完全但对称的股票波动性价值曲线的上方,表明当没有现金红利时,同等条件下市场参与者的完全信息会带来更高的股票波动性价值,虽然这里列示的股票波动性价值数值并不大,但结果符合正常的逻辑,即信息完全较信息不完全可能带给市场参与者更多的价值。
(a)q=0
(b)q=0.06
(c)q=0.12
图3不同现金红利率水平下信息不完全或不对称的效应分析
Figure3EffectAnalysisofIncompleteorAsymmetricInformationforDifferentCashDividendRates
图3(b)中,信息完全且对称与信息不完全但对称的两条股票波动性价值曲线基本重合,随着q继续增加,图3(c)中,信息不完全但对称的股票波动性价值曲线逐渐越过信息完全且对称的曲线,信息不完全但对称的股票波动性价值已经大于信息完全且对称的股票波动性价值。
结合市场参与者不同的交易动机及信息视角考虑,可以认为,信息完全且对称条件下,当没有现金红利或现金红利率水平很低时,市场参与者的类型往往属于市场型,他们希望通过价格的波动获取收益。因此,波动对他们而言是有价值的,但是随着现金红利率水平上升,波动为他们带来的价值会相对下降,尤其当现金红利率水平达到一定高度时,他们将不再在意波动可能带来的收益,因而成为价值型市场参与者。当信息不完全但对称时,如果现金红利率水平低或者为零,交易动机视角下,市场参与者毫无疑问也应属于市场型参与者,但由于其掌握的信息有限,导致部分决策失误,阻碍了他们获得正常的股票波动性价值,因此股票波动性价值曲线处于信息完全且对称曲线的下方。
当现金红利率水平不断上升,交易动机视角下,由于现金红利率能够在一定程度上满足市场参与者对收益的需要,因此股票波动性价值逐渐下降。当现金红利率与无风险收益率基本相等时,达到波动性价值与风险的临界点。由于此时股票波动性价值的绝对值相对较小,因而信息视角下,不完全信息带来的股票波动性价值的损失就更小,表现在股票波动性价值曲线上,如图3(b)所示,信息完全且对称与信息不完全但对称的股票波动性价值曲线基本重合。
当现金红利率水平进一步提高,持有成本开始变为负值,交易动机视角下,此时的市场参与者大多属于价值型参与者,波动对他们而言更多表现为风险,于是在图3(c)中,信息完全且对称的股票波动性价值曲线始终处于小于0的位置。与此同时,信息视角下,信息不完全但对称的股票波动性价值却仍然受到信息不完全的限制,从绝对值上看,小于信息完全且对称的值,不同的是,此时的股票波动性价值为负,表现为风险。由此,可以解释图3(c)中,信息不完全但对称的股票波动性价值曲线反而位于信息完全且对称的曲线上方的现象。
此外,观察图3中3幅子图中分别代表信息不完全且不对称条件的两条曲线,它们随波动率水平的提高均呈发散的态势,表明与对称信息条件相比,市场参与者信息水平的差异将放大股票波动性价值。同时,对比3幅子图纵坐标发现,不同现金红利水平下,股票波动性价值被放大的程度并无显著差异,均为30%~40%之间。
综上,信息不完全但对称条件下,股票波动性价值的绝对值受信息不完全的影响,且这种影响的程度随现金红利率水平的提高而增大;信息不完全且不对称条件下,信息优势将极大地放大股票波动性价值,放大的方向与信息优势所处的方向一致,且波动率水平越高,放大效应越明显;信息不完全且不对称条件下,信息优势对股票波动性价值的放大作用与现金红利率水平无关。
4.2.3 信息视角下不同现金红利率水平的股票波动性价值曲线形态分析
图4和图5分别给出现金红利率为0和0.12时不同信息条件下的股票波动性价值曲线,其中,S=10,T=1,r=0.06。
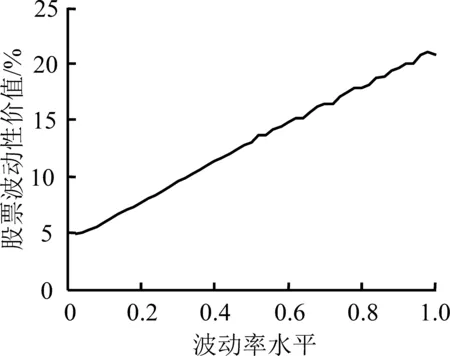
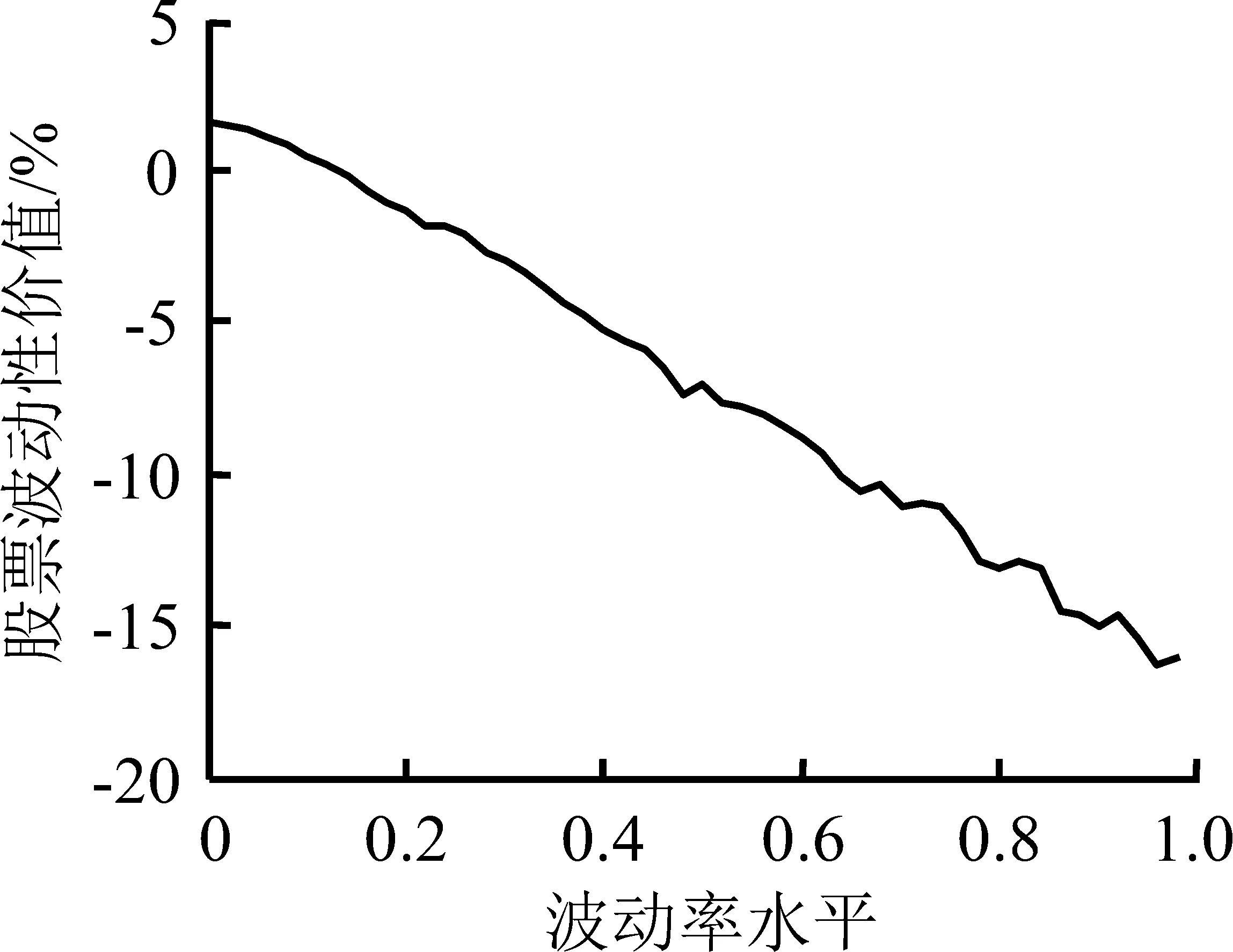
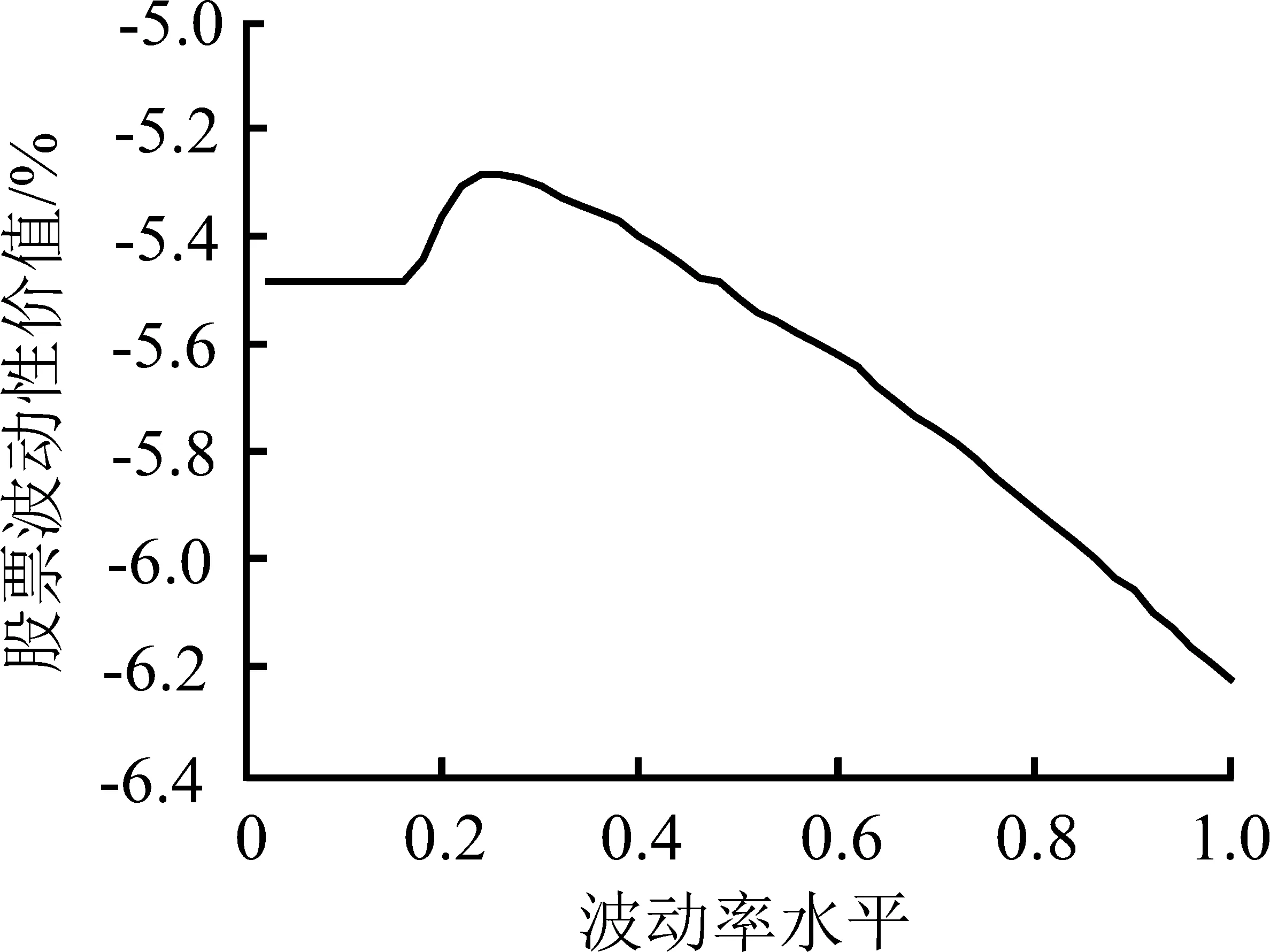
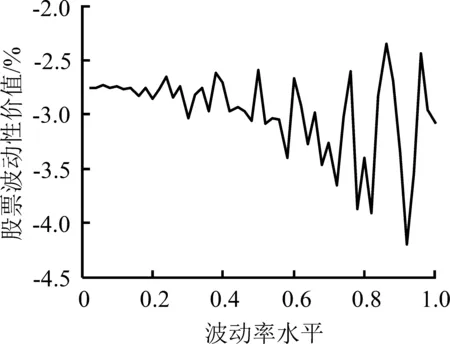
图4(a)和图5(a)给出信息完全且对称条件下,不同现金红利率水平的股票波动性价值的不同表现形式。图4(b)、(c)、(d)和图5(b)、(c)、(d)分别给出信息不完全但对称、信息不完全且不对称-波动收益性期权信息占优和信息不完全且不对称-波动损失性期权信息占优的条件下,不同现金红利率水平的股票波动性价值,3种条件下在q=0和q=0.12时并未表现出显著不同的形态,且在以0.01为间隔时所有q取不同值的情况下均得到类似的结论。由此再次证明,信息不完全、不对称将有可能改变市场参与者对价值型和市场型的定位,虽然现金红利仍然受到欢迎,但波动可能带来收益的预期在信息优势的催化下得到放大,以图4(a)和图4(c)、图5(a)和图5(c)为例,比较可知,任何波动率水平下,存在信息优势的(c)图的股票波动性价值都高于(a)图,且波动率水平越高,这种差异越明显。更重要的是,(c)图中,股票波动性价值曲线表现为向右上方倾斜的趋势,表明市场参与者已经不再如完全信息条件下那样,充分考虑现金红利率带来的收益,在一定的波动率水平上表现出不同的交易动机,而是直接关注波动可能带来的、远远高于现金红利率水平的收益。

(a)信息完全且对称
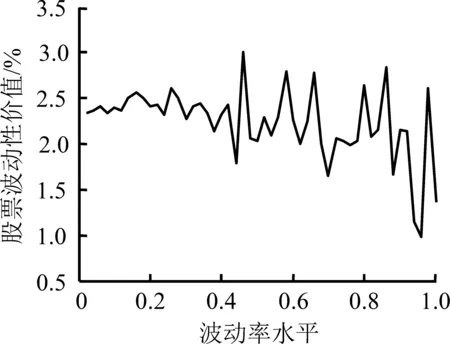
(b)信息不完全但对称
(c)信息不完全且不对称-波动收益性期权信息占优
(d)信息不完全且不对称-波动损失性期权信息占优
图4q=0时信息不完全或不对称的股票波动性价值曲线
Figure4CurveofStocks′VolatilityValueundertheConditionofIncompleteorAsymmetricInformationWhenq=0
(a)信息完全且对称
(b)信息不完全但对称
(c)信息不完全且不对称-波动收益性期权信息占优
(d)信息不完全且不对称-波动损失性期权信息占优
图5q=0.12时信息不完全或不对称的股票波动性价值曲线
Figure5CurveofStocks′VolatilityValueundertheConditionofIncompleteorAsymmetricInformationWhenq=0.12
因此,信息视角下,由于信息不完全或不对称的影响,股票波动性价值曲线在不同现金红利率水平下的不同表现不复存在,仅表现为信息不对称对股票波动性价值的放大作用以及信息不完全对股票波动性价值的抵减和干扰作用,抵减表现为股票波动性价值绝对值的减小,干扰表现为股票波动性价值的不稳定。
对比图4和图5中子图(a)和子图(d)可以发现,负的股票波动性价值,也就是波动性风险也同样会被放大。市场参与者的立场和思路与本研究对子图(c)的分析类似,但方向相反。
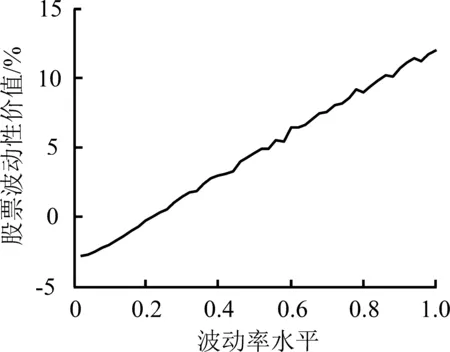
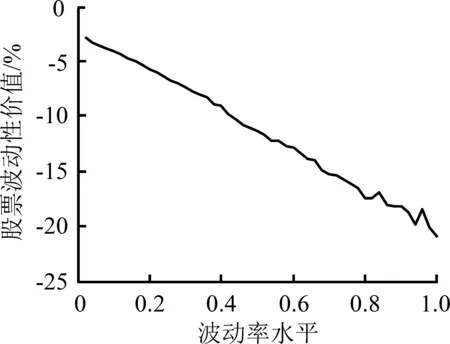
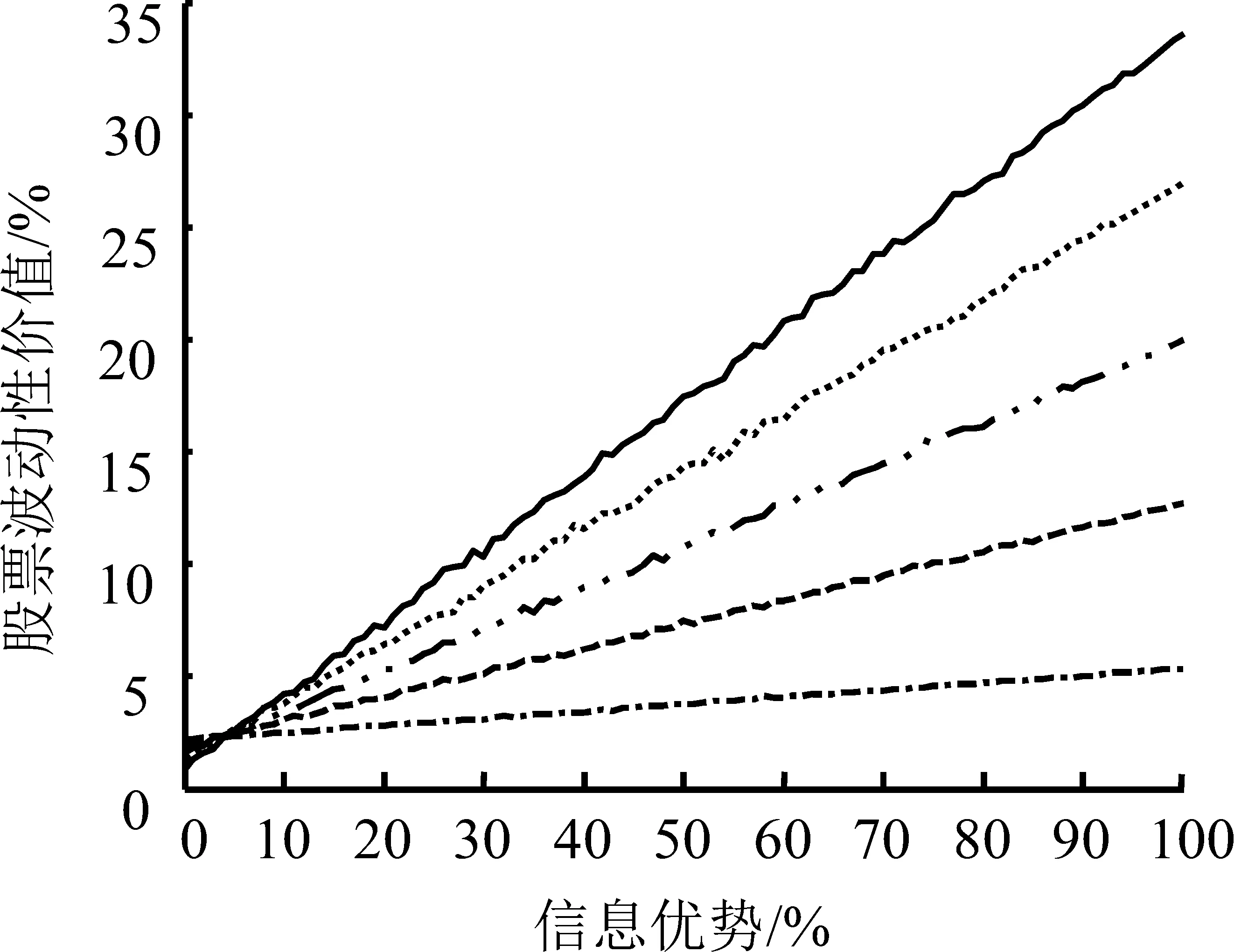
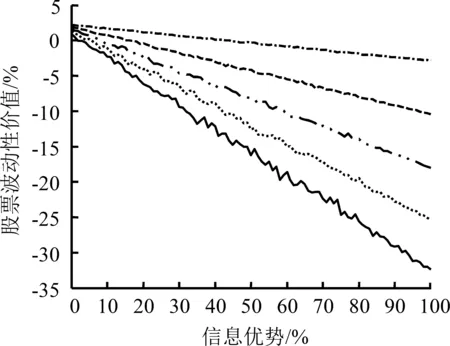
4.3 信息不对称水平对股票波动性价值的影响
令S=10,T=1,r=0.06,q=0.03,σ取值分别为0.10、0.30、0.50、0.70、0.90,图6给出不同波动率水平下信息不对称程度对股票波动性价值的影响。
为方便计算,本研究在求解过程中对信息不对称的度量按如下方法处理。
(1)将信息占优的一方设为完全信息;
(2)将信息不占优的一方设为不完全信息;
(3)图中横坐标表示信息优势方对劣势方多占有的信息的比例,0%表示信息优势方与信息劣势方拥有同样多的信息,即双方都是完全信息。100%表示信息优势方比信息劣势方多占有100%的信息,即处于信息优势的一方为完全信息,处于信息劣势的一方为完全无信息。以此类推,如果50%的信息优势,则表示信息优势方比信息劣势方多占有50%的信息。因此,横坐标从左到右表示信息不对称程度逐渐扩大。
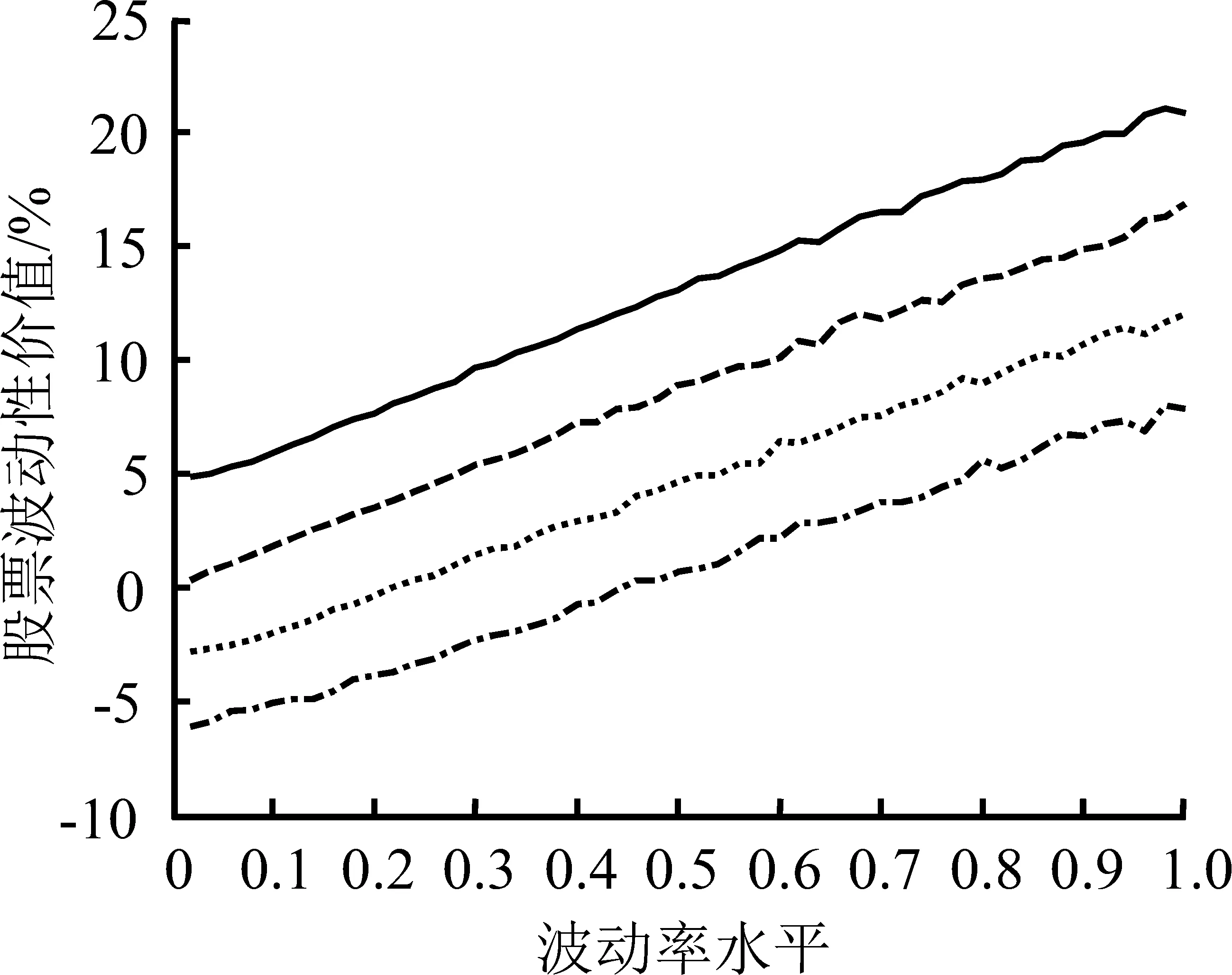
对比图6(a)和图6(b),总体上,随着期权博弈双方信息差异的扩大,股票波动性价值的绝对值迅速增加,表明信息差异可以在很大程度上影响股票波动性价值。
具体而言,①波动率水平越高,曲线斜率的绝对值越大,曲线表现越陡峭,单位信息优势对股票波动性价值的影响越大,股票波动性价值对信息变化的反应越敏感;②股票波动性价值被放大的方向与信息优势的方向一致;③波动率水平的提高,不仅能加大股票波动性价值被放大的程度,也能增加股票波动性价值的波动,表现为高波动率水平的股票波动性价值曲线相对更不平滑。
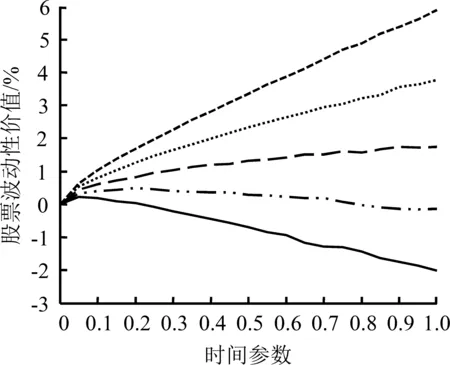
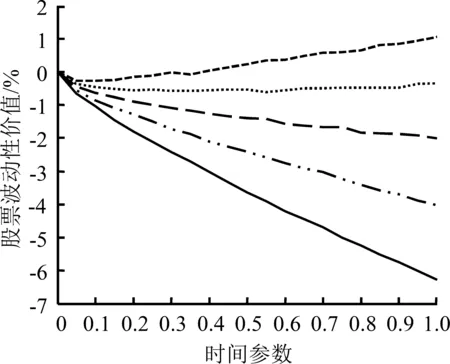
4.4 时间参数对股票波动性价值的影响
不对称信息条件下,时间参数T对股票波动性价值的影响见图7。S=10,σ=0.10,r=0.06,q取值分别为0、0.03、0.06、0.09和0.12,T在区间[0,1]变动时股票波动性价值的变化情况。
(a)信息不完全且不对称-波动收益性期权信息占优
(b)信息不完全且不对称-波动损失性期权信息占优
图6信息视角下信息不完全或不对称水平对股票波动性价值的影响
Figure6InfluenceofIncompleteorAsymmetricInformationtoStocks′VolatilityValueBasedonInformationalPerspective
(a)信息不完全且不对称-波动收益性期权信息占优
(b)信息不完全且不对称-波动损失性期权信息占优

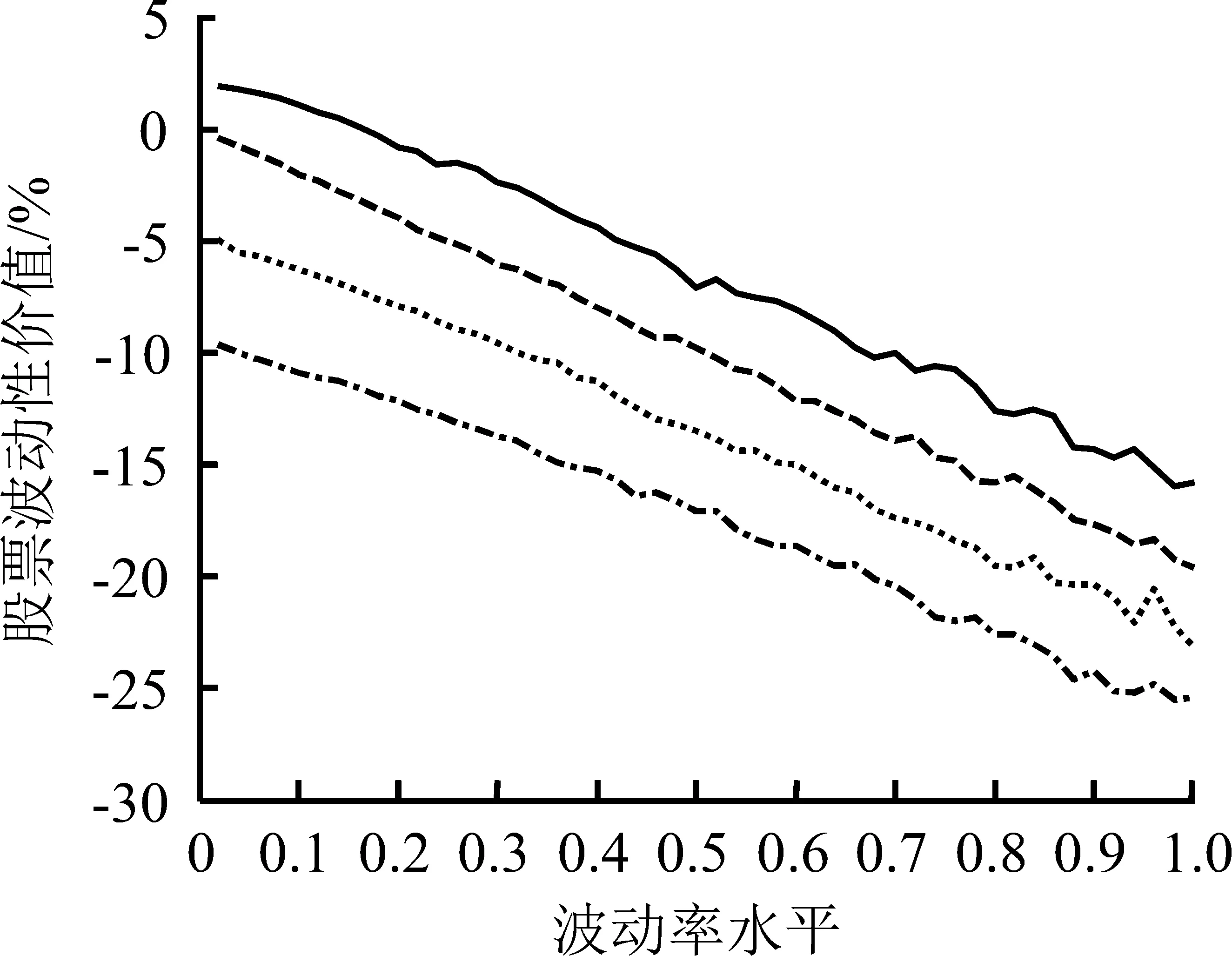
图7信息视角下时间参数对股票波动性价值的影响
Figure7InfluenceofTimeParametertoStocks′VolatilityValueBasedonInformationalPerspective
无论股票波动表现为价值还是风险,无论处于何种信息条件,股票波动性价值的绝对值都随T的增大而增大。
根据图7,一方面,时间参数的作用强度与现金红利率水平有关,如果股票波动性价值为正,现金红利率越低作用越明显;如果股票波动性价值为负,现金红利率越高作用越明显。对比图7(a)和图7(b),图7(a)中q=0的波动性曲线最陡峭,图7(b)中q=0.12的波动性曲线斜率最大。
另一方面,时间参数的作用强度取决于股票波动性价值的方向,即时间参数对股票波动性价值的影响主要表现在对其绝对值的放大效应上。
因此,信息视角下时间参数对股票波动性价值的影响主要表现在对股票波动性价值数量上的放大,但不会改变股票波动性价值本身的方向;与此同时,当股票波动性价值的方向与市场参与者信息优势的方向一致时,放大效应更加明显。
4.5 股票初始价格和无风险收益率对股票波动性价值的影响
信息视角下,股票的初始价格S和无风险收益率r对股票波动性价值没有显著影响,这一结论与完全信息条件下的结论类似,不再进行详细论述。
5 结论
本研究探讨信息视角下基于异质信念的股票波动性价值,基于市场参与者异质性假设,构建信息视角下的股票波动性价值模型,并描述信息不完全或不对称条件下股票波动性价值的分布特征,得到以下结论。
(1)相对于信息不完全,信息不对称是决定股票波动性价值大小和方向的首要因素,能明显放大波动率水平、现金红利率水平、时间参数等对股票波动性价值的影响。当拥有信息优势时,市场参与者不仅可能偏好较高的波动率水平,而且可能从根本上改变对波动的态度,由一个价值型的市场参与者转变成一个市场型的参与者,并充分享有由波动带来的收益,而处于信息劣势的市场参与者则将承担对应的损失,波动率水平本身将进一步放大这种现象。由此可知,信息不对称将加剧市场波动,加大股票波动性价值的不确定性,改变市场参与者的交易动机。
(2)不完全但对称的信息条件,会使股票波动性价值较其他参数相同时完全信息条件下的数值更小,但不会改变股票波动性价值的方向。
(3)关于波动率水平对股票波动性价值的影响。信息不对称条件下,信息优势的存在使市场参与者对波动率水平的变化更加敏感,股票波动性价值曲线斜率的绝对值更大,单位波动率水平变化导致的股票波动性价值变化更大。但在不完全但对称的信息背景下,主要表现为随着波动率水平的增加,股票波动性价值的稳定性下降。
(4)无论信息条件如何,股票波动性价值都随着现金红利率水平的提高而下降,即信息水平不改变股票波动性价值与现金红利率水平之间的负相关关系;同时,无论波动表现为价值还是风险,股票波动性价值的绝对值都随时间参数的增大而增大。
信息视角下,基于异质信念的股票波动性价值模型,从理论角度解释了信息水平及其状态对股票价格行为的作用机制及表现形式,本研究结论在一定程度上完善了资产定价理论体系,不仅能为监管部门进一步完善交易制度、加强市场信息建设、规范信息披露行为等政策措施提供理论依据,也能帮助市场参与者深入认识股票价格的形成过程,了解市场微观结构,进而提高投资决策效率,规避风险。
关于股票波动性价值的研究尚处于探索阶段,本研究还存在一些局限和不足。从定量角度进一步分析信息优势对股票波动性价值和波动性风险影响程度的差异,以及继续修正现有模型假设,考虑基于信息的市场参与者有限理性对股票波动性价值的影响,都是未来有意义的研究方向。
参考文献:
[1]吴冲锋,王柱,冯芸.基于资产链的资产定价问题的思考.管理科学学报,2008,11(1):1-11.
WU Chongfeng,WANG Zhu,FENG Yun.Asset pricing based on asset chains.JournalofManagementSciencesinChina,2008,11(1):1-11.(in Chinese)
[2]LONGSTAFF F A.How much can marketability affect security values?.TheJournalofFinance,1995,50(5):1767-1774.
[3]LONGSTAFF F A.Placing no-arbitrage bounds on the value of nonmarketable and thinly-traded securities∥BOYLE P,LONGSTAFF F A,PITCHKEN P.AdvancesinFuturesandOptionsResearch.Bingley,BD:Emerald Group Publishing Limited,1995,8:203-228.
[4]LONGSTAFF F A.Optimal portfolio choice and the valuation of illiquid securities.TheReviewofFinancialStudies,2001,14(2):407-431.
[5]吴卫星,汪勇祥,成刚.信息不对称与股权结构:中国上市公司的实证分析.系统工程理论与实践,2004,24(11):28-32.
WU Weixing,WANG Yongxiang,CHENG Gang.Asymmetric information and ownership structure:evidence from China listed companies.SystemsEngineering-Theory&Practice,2004,24(11):28-32.(in Chinese)
[6]KOZIOL C,SAUERBIER P.Valuation of bond illiquidity:an option-theoretical approach.TheJournalofFixedIncome,2007,16(4):81-107.
[7]梁朝晖,张维.流动性的期权定价方法.北京航空航天大学学报:社会科学版,2005,18(3):8-11.
LIANG Zhaohui,ZHANG Wei.Valuation of liquidity:an option-theoretical approach.JournalofBeijingUniversityofAeronauticsandAstronautics:SocialSciencesEdition,2005,18(3):8-11.(in Chinese)
[8]WEBER P,ROSENOW B.Large stock price changes:volume or liquidity?.QuantitativeFinance,2006,6(1):7-14.
[9]MIKE S,FARMER J D.An empirical behavioral model of liquidity and volatility.JournalofEconomicDynamics&Control,2008,32(1):200-234.
[10] ANG A,HODRICK R J,XING Y,et al.The cross-section of volatility and expected returns.TheJournalofFinance,2006,61(1):259-299.
[11] ADRIAN T,ROSENBERG J.Stock returns and volatility:pricing the short-run and long-run components of market risk.TheJournalofFinance,2008,63(6):2997-3030.
[12] BOLLERSLEV T,KRETSCHMER U,PIGORSCH C,et al.A discrete-time model for daily S&P500 returns and realized variations:jumps and leverage effects.JournalofEconometrics,2009,150(2):151-166.
[13] 郑振龙,汤文玉.波动率风险及风险价格:来自中国A股市场的证据.金融研究,2011(4):143-157.
ZHENG Zhenlong,TANG Wenyu.Volatility risk and its price:the evidence from Chinese A-share market.JournalofFinancialResearch,2011(4):143-157.(in Chinese)
[14] 陈蓉,方昆明.波动率风险溢酬:时变特征及影响因素.系统工程理论与实践,2011,31(4):761-770.
CHEN Rong,FANG Kunming.Volatility risk premium in Hong Kong stock market.SystemsEngineering-Theory&Practice,2011,31(4):761-770.(in Chinese)
[15] 陈炜,袁子甲,何基报.异质投资者行为与价格形成机制研究.经济研究,2013,48(4):43-54.
CHEN Wei,YUAN Zijia,HE Jibao.The study on behavior of heterogeneous investor and price information.EconomicResearchJournal,2013,48(4):43-54.(in Chinese)
[16] HO H C,LIN C C.Influence of heterogeneous beliefs on volatility when agents′ degree of confidence differs.AppliedEconomicsLetters,2011,18(10):955-959.
[17] DUMAS B,KURSHEV A,UPPAL R.Equilibrium portfolio strategies in the presence of sentiment risk and excess volatility.TheJournalofFinance,2009,64(2):579-629.
[18] 张宗新,王海亮.投资者情绪、主观信念调整与市场波动.金融研究,2013(4):142-155.
ZHANG Zongxin,WANG Hailiang.Investor sentiment,subjective belief adjustment and market fluctuations.JournalofFinancialResearch,2013(4):142-155.(in Chinese)
[19] 朱宏泉,余江,陈林.异质信念、卖空限制与股票收益:基于中国证券市场的分析.管理科学学报,2016,19(7):115-126.
ZHU Hongquan,YU Jiang,CHEN Lin.Heterogeneous beliefs,short-sale constraints and stock returns:evidence from China.JournalofManagementSciencesinChina,2016,19(7):115-126.(in Chinese)
[20] 虞文微,张兵,赵丽君.异质信念、卖空机制与“特质波动率之谜”:基于2 698家中国A股上市公司的证据.财经科学,2017(2):38-50.
YU Wenwei,ZHANG Bing,ZHAO Lijun.Heterogeneous information,short selling and the idiosyncratic volatility puzzle:based on the evidence from 2 698 listed companies from China′s A stock market.Finance&Economics,2017(2):38-50.(in Chinese)
[21] 张普,吴冲锋.基于期权博弈的股票波动性价值模型.系统工程理论与实践,2012,32(8):1631-1638.
ZHANG Pu,WU Chongfeng.Model of stocks′ volatility value based on option games.SystemsEngineering-Theory&Practice,2012,32(8):1631-1638.(in Chinese)
[22] JIN L,MYERS S C.R2around the world:new theory and new tests.JournalofFinancialEconomics,2006,79(2):257-292.
[23] LEE S S.Jumps and information flow in financial markets.TheReviewofFinancialStudies,2012,25(2):439-479.
[24] 刘志东,杨竞一.基于非参数日内跳跃检验和高频数据的公司信息披露对股市价格波动影响研究.中国管理科学,2016,24(10):22-34.
LIU Zhidong,YANG Jingyi.A study of firm specific information disclosure on the price variation with nonparametric intraday jumps detection in high frequency data.ChineseJournalofManagementScience,2016,24(10):22-34.(in Chinese)
[25] 王冲,谢雅璐.会计稳健性、信息不透明与股价暴跌风险.管理科学,2013,26(1):68-79.
WANG Chong,XIE Yalu.Accounting conservatism,information opacity and stock price crash risk.JournalofManagementScience,2013,26(1):68-79.(in Chinese)
[26] 文凤华,龚旭,黄创霞,等.股市信息流对收益率及其波动的影响研究.管理科学学报,2013,16(11):69-80.
WEN Fenghua,GONG Xu,HUANG Chuangxia,et al.Impact of information flow on returns and return volatility in Chinese stock market.JournalofManagementSciencesinChina,2013,16(11):69-80.(in Chinese)
[27] CALLEN J L,FANG X.Institutional investor stability and crash risk:monitoring versus short-termism?.JournalofBanking&Finance,2013,37(8):3047-3063.
[28] AN H,ZHANG T.Stock price synchronicity,crash risk,and institutional investors.JournalofCorporateFinance,2013,21:1-15.
[29] 宋小保.企业盈利能力、机构投资者与股票波动风险.管理工程学报,2015,29(2):121-129.
SONG Xiaobao.Profitability,institutional investor and stock volatility risk.JournalofIndustrialEngineeringandEngineeringManagement,2015,29(2):121-129.(in Chinese)
[30] 许年行,于上尧,伊志宏.机构投资者羊群行为与股价崩盘风险.管理世界,2013(7):31-43.
XU Nianhang,YU Shangyao,YI Zhihong.Institutional investor herding and stock price crash risk.ManagementWorld,2013(7):31-43.(in Chinese)
[31] 程天笑,刘莉亚,关益众.QFII与境内机构投资者羊群行为的实证研究.管理科学,2014,27(4):110-122.
CHENG Tianxiao,LIU Liya,GUAN Yizhong.The empirical research of herding behavior between QFII and domestic institutional investors.JournalofManagementScience,2014,27(4):110-122.(in Chinese)
[32] GALARIOTIS E C,RONG W,SPYROU S I.Herding on fundamental information:a comparative study.JournalofBanking&Finance,2015,50:589-598.
[33] 邢治斌,仲伟周.机构持股、分析师跟进与股票波动关系研究:基于联立方程组模型的实证分析.湖南师范大学社会科学学报,2014,43(2):120-127.
XING Zhibin,ZHONG Weizhou.Research on the relationship of institutional ownership,analyst follow-up and stock volatility:an empirical study of nonlinear simultaneous equations mode.JournalofSocialScienceofHunanNormalUniversity,2014,43(2):120-127.(in Chinese)
[34] 代昀昊,唐齐鸣,刘莎莎.机构投资者、信息不对称与股价暴跌风险.投资研究,2015,34(1):50-64.
DAI Yunhao,TANG Qiming,LIU Shasha.Institutional investors,asymmetric information and stock price crash risk.ReviewofInvestmentStudies,2015,34(1):50-64.(in Chinese)
[35] BRADLEY D,CLARKE J,LEE S,et al.Are analysts′ recommendations informative?Intraday evidence on the impact of time stamp delays.TheJournalofFinance,2014,69(2):645-673.
[36] FANG L H,YASUDA A.Are stars′ opinions worth more?The relation between analyst reputation and recommendation values.JournalofFinancialServicesResearch,2014,46(3):235-269.
[37] SIMON A,NOWLAND J.Long-term growth forecasts and stock recommendation profitability.Asia-PacificJournalofAccounting&Economics,2015,22(2):163-190.
[38] 肖土盛,宋顺林,李路.信息披露质量与股价崩盘风险:分析师预测的中介作用.财经研究,2017,43(2):110-121.
XIAO Tusheng,SONG Shunlin,LI Lu.Information disclosure quality and stock price crash risk:the mediating role of analyst forecast.JournalofFinanceandEconomics,2017,43(2):110-121.(in Chinese)
[39] LONGSTAFF F A,SCHWARTZ E S.Valuing American options by simulation:a simple least-squares approach.TheReviewofFinancialStudies,2001,14(1):113-147.
[40] GLASSERMAN P,YU B.Simulation for American options:regression now or regression later?∥NIEDERREITER H.MonteCarloandQuasi-MonteCarloMethods2002.Berlin Heidelberg:Springer-Verlag,2004:213-226.

