基于MIMU的输电线路振动分析

杨金显， 杨 闯， 李双磊， 蒋志涛， 王鹏飞(.河南理工大学 电气工程与自动化学院，河南 焦作 454003；.国网山东临朐县供电公司，山东 临朐 6600)

输电线路是输电的纽带，特别是特高压输电线路，保证其安全运行至关重要，尤其在特高压输电工程所采用的导线截面、悬挂点高度以及档距都有所增大，其风致振动非常严重。按频率和振幅划分，主要为高频微幅的微风振动、中频中幅的次档距振荡和低频大振幅的舞动[1]，三种振动都会给输电线路造成破坏，容易引起导线疲劳断股、金具损坏、相间闪络，造成线路跳闸停电或引起烧伤或折断导线，杆塔倒塌等严重事故，严重影响特高压输电线路的安全运行，需要设计阻尼控制器减缓输电线路的振动。阻尼控制器的设计与输电线路振动幅度和频率直接相关，不同地区输电线路振动幅度和频率不同，阻尼器的设计参数也不同，为最大程度发挥阻尼器性能，必须结合本地区长期输电线路振动特性，因此对输电线路振动幅度和频率的分析就变的至关重要。

近年来，基于MEMS加速度计/陀螺仪的微惯性姿态测量单元(MIMU)以其成本低、体积小、寿命长、集成化、抗冲击能力强和可靠性高等优势，发展迅猛，应用广泛，可进行输电线振动信息的检测，引起了诸多研究人员关注：张帆等[2-3]最初采用MEMS加速度计多点监测输电线振动加速度，忽略输电线扭转影响通过积分解算输电线运动轨迹等参数；王有元等[4]通过重新标定积分基线以抑制因加速度积分产生的轨迹发散，利用加速度分解合成关系推导转换公式以消除传感器扭转引起的误差；黄新波等[5]为避免导线舞动扭转导致计算出的相对位移与实际运动偏差，设计了基于MIMU和ZigBee无线组网的导线舞动多点监测系统；邵颖彪等[6]为克服传统只用加速度计监测导线舞动只能得到位移的缺陷，设计了基于MIMU/磁强计的输电导线姿态解算多点监测方案。上述这些装置或方法采用惯性测量来实现导线的定位，计算轨迹(姿态和位置)，进而获取输电线路风致振动幅度和频率，难度十分巨大，能够实现这些功能需要导航级惯性导航系统，体积和成本都会很大，另外惯性测量存在需要初始值和随着时间的积累误差会越来越大的缺点，会导致最后无法测量，不能长期计算导线振动幅度和频率。由于特高压导线周围有强磁场干扰加上输电导线安装监测节点困难，通过ZigBee等无线组网将档距内多个MIMU或MIMU/磁强计监测节点互联的多点监测方案很难实施。

从振动成分来看，任何复杂振动都是由不同振动成分组成的，关键找出振动的主要部分——几种基本的模式振动分量。尽管输电线路振动包括各种复杂的运动(幅度和频率都会发生变化)，但其基本模式是平动和扭转[7]，因此可通过对输电线路平动和扭转分析以了解其振动特性(振幅和频率)。输电线路在绝缘子串悬挂点受力情况最为复杂，最易因输电线路振动发生故障，更重要的是悬挂点包含更多输电线路振动信息，输电线路正常运行时，悬挂点振动角一般在30′～50′，导线振动幅度越大，振动角越大，导线舞动时，振动角接近10°，另外在该处安装监测设备也容易实现，因此，可通过采集此处平动和扭转信息，来计算输电线路振动幅度和频率[8-11]。

悬挂点采集的平动和扭转信号较弱，极易受周围磁场干扰，鉴于此，设计一种MIMU测量节点，并采用一定长度的弹性杆进行信号物理放大和防电磁干扰，为提高系统精度，实现长期监测输电线路振动幅度和频率，不利用加速度和角速度的解算信息，而直接通过监测加速度时间序列的二阶矩来计算数据的变异度，预测输电线路平动及扭转的幅度；通过对监测数据的相似性分析，预测输电线路平动及扭转的频率；最后设计了振动台、转台试验和输电线路模型模拟实验，实验结果表明处理数据结果能够反映输电线路振动变化规律，说明输电线路振动分析方法是有效的，可以为输电线路的运动阻尼控制参数计算提供参考。

1 MIMU数据采集与处理

1.1 MIMU测量系统

MIMU作为输电线运动监测节点通过延长杆固连于杆塔绝缘子串悬挂点处，如图1所示，延长杆的使用一是为了监测节点和导线有一定的距离，减小电磁干扰；二是为了增大观测能力，由于实际的监测节点不能安装在导线上(特高压导线强磁干扰，且安装困难)，但又不能降低监测的能力，为了增大观测能力，采用具有一定弹性、一定长度的杆。弹性杆长度满足共振的范围要求，使输电导线振动时满足振幅最大，最大程度的敏感振动幅度、频率及变化趋势，由于输电导线振动频率较小且是变化的，不会使弹性杆振坏。MIMU采集的数据经光纤传至杆塔处理器进行后续数据处理，为减少输电线路电磁场干扰，杆塔处理器通过刚性杆向空中延伸。

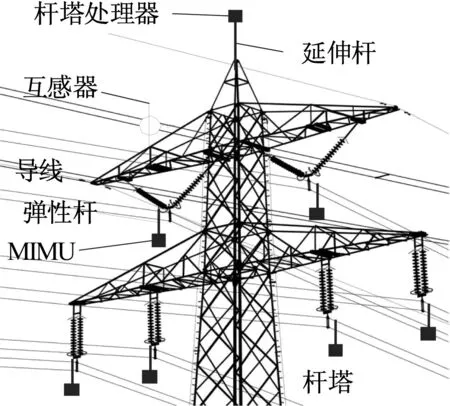
图1 输电线路模型及MIMU布置图Fig.1 Transmission lines model and MIMU layout

1.2 MIMU数据AR-Kalman滤波处理

由于MIMU加速度计读数为合加速度A，包含振动加速度a，重力加速度g和测量噪声ε，进行平动和扭转分析需提取振动加速度(平动方向，即水平和垂直方向，下同)和重力加速度。MIMU振动加速度及重力加速度通过MIMU角速度信息辅助提取[12-13]，通过AR-Kalman对其进一步降噪。

对MIMU加速度信号(振动、重力加速度)建立时间序列模型时，须对提取的振动、重力加速度数据预处理，使其满足平稳随机序列，以对其建立时序模型。本文综合考虑AIC准则、模型适用性和系统实时性要求，选用AR(2)模型分别对提取的运动加速度a和重力加速度g进行建模[14-15]，根据观测量at(振动加速度)、gt(重力加速度)，通过最小二乘法拟合自回归参数α1、α2、β1、β2，分别得其AR(2)模型

at=α1at-1+α2at-2+εat

gt=β1gt-1+β2gt-2+εgt

建立输电线路加速度AR(2)模型后，采用Kalman滤波进一步降噪提高信号精度，状态方程为

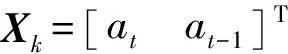
将上述状态参数带入Kalman滤波公式计算运动加速度最优滤波值[16](重力加速度处理流程相同)。

2 输电线路振动分析

2.1 输电线路平动特征提取

输电线路平动时，会出现X,Y,Z三个轴的平动，如图2所示，平动幅度与输电线路所受外界合冲击加速度有关，冲击加速度越大，平动幅度越大，平动幅度近似正比于输电线路振动加速度a，因此输电线路的平动必然会引起振动加速度监测数据的变化，选取振动加速度信号时间序列作为平动特征量，记为ak，为消除偶然误差同时压缩数据量，对其进行滑动分段模式表示。将AR-Kalman滤波处理的振动加速度数据每L个为一组，每滑动l个数取一次平均，第i段记为ai(ai1,ai2,ai3,…,aiN)，其中N=L/l，ain为

(1)

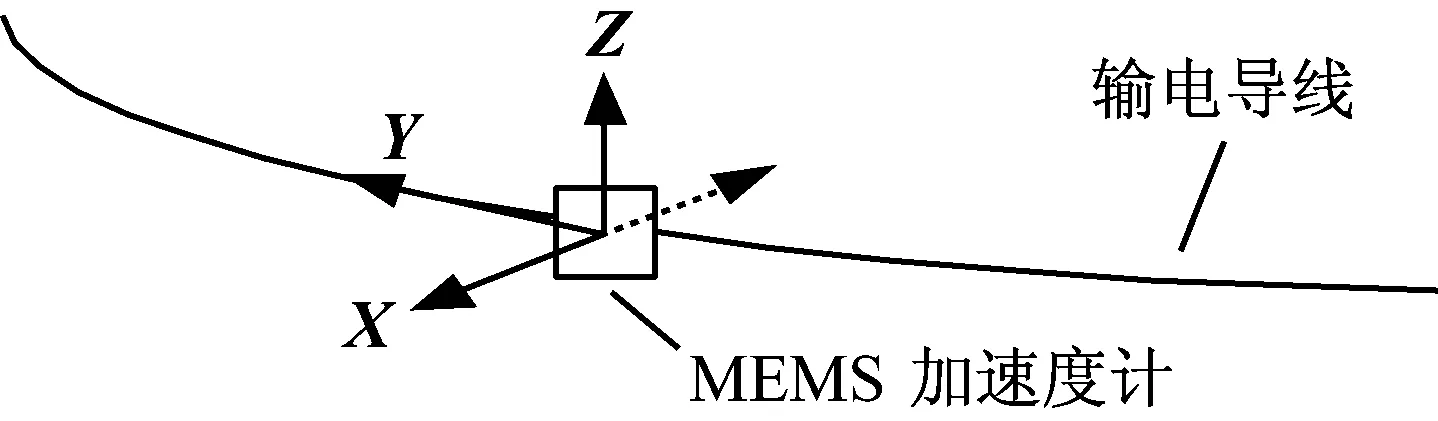
图2 输电线平动示意图Fig.2 Transmission line translational movement

将输电线路静止条件下振动加速度数据作为初始时间序列数据段，初始序列段均值记为a0。加速度数据每次变化的大小和这些变化的方向及持续时间，表示输电线路所受外界冲击力情况，也即平动幅度变化情况(冲击力越大平动幅度越大)，通过计算ai相对a0二阶中心距Dai0，获取振动加速度数据变异情况，进而根据变异情况预测输电线路平动幅度，Dai0为

(2)

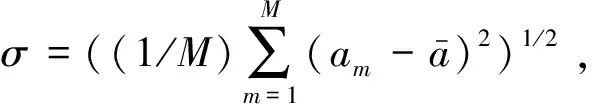
振动加速度数据变化频率也即输电线路振动频率。通过计算ai与ai+1欧式距离Daii+1，度量相邻两段序列的相似性，以测度振动加速度数据变异速率，进而根据变异速率判断输电线路平动频率(欧式距离越大，相邻两序列段数据相似性越低，运动加速度数据变异越大，相邻两段数据序列变化越快，输电线路平动加速度频率越大)，Daii+1为

(3)

为便于预测平动幅度及频率，将Dai0、Daii+1进行归一化处理，分别记为Da(表示平动程度)、Fa(平动频率系数)，即

Da=Dai0/Damax+ε1

(4)

Fa=Daii+1/DEamax+ε2

(5)

式中:Damax为设定的输电线路最大运动加速度二阶中心距，DEamax为设定的输电线路相邻运动加速度序列段最大欧式距离，ε为误差因子。

2.2 输电线路扭转特征提取

沿输电导线轴向观察图2，未发生或轻微扭转时，重力加速度分量主要集中在Z轴，此时加速度计X轴敏感的重力加速度为0或约为0，如图3(a)所示；发生扭转运动时，Z轴向敏感的重力加速度分量会转移或部分转移给X轴，即扭转运动时Z轴和X轴发生交叉耦合运动。Z轴向X轴转移的重力加速度分量越多也即Z轴重力加速度分量越小，X轴重力加速度分量越大，说明输电导线扭转程度越大，如图3(b)所示。因此输电线路的扭转必然会引起X轴Z轴重力加速度监测数据的变化，选取X轴Z轴重力加速度增广信号[X,Z]时间序列作为扭转特征量，记为gk(X,Z)，为消除偶然误差同时压缩数据量，对其进行滑动分段模式表示。将AR-Kalman滤波处理的X轴Z轴重力加速度数据每L个为一组，每滑动l个数取一次平均，第i段记为:gi(gi1,gi2,gi3,…,giN)，其中N=L/l，gin为

(6)

将输电线路静止条件下重力加速度数据作为初始时间序列数据段，初始序列段均值记为g0。重力加速度数据每次变化的大小和这些变化的方向及持续时间，表示输电线路扭转程度，通过计算gi相对g0二阶中心距Dgi0，获取重力加速度数据变异情况，进而根据变异情况预测输电线路扭转程度，Dgi0为

(7)

重力加速度数据变化频率也即输电线路扭转的频率。通过计算gi与gi+1欧式距离Dgii+1，度量相邻两段序列的相似性，以测度重力加速度数据变异速率，进而根据变异速率判断输电线路扭转频率，Dgii+1如下

(8)

把Dgi0、Dgii+1进行归一化处理，分别记为Dg(扭转程度)、Fg(扭转频率系数)，即

Dg=Dgi0/Dgmax+ε3

(9)

Fg=Dgii+1/DEgmax+ε4

(10)

其中Dgmax为设定的输电线路最大增广重力加速度二阶中心距，DEgmax为设定的相邻增广重力加速度序列段最大欧式距离，ε为误差因子。

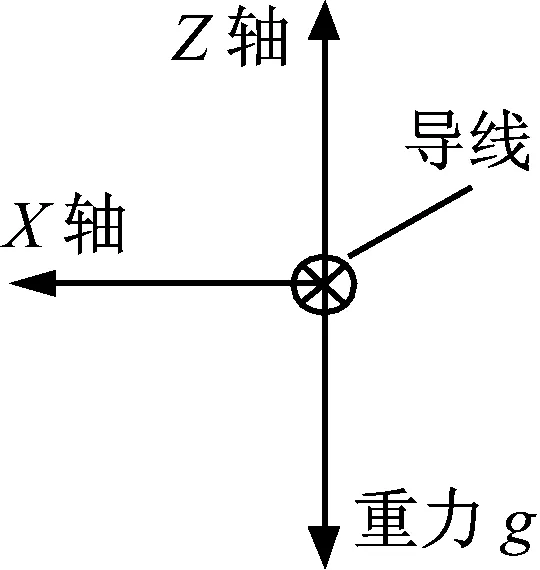
(a) 未扭转

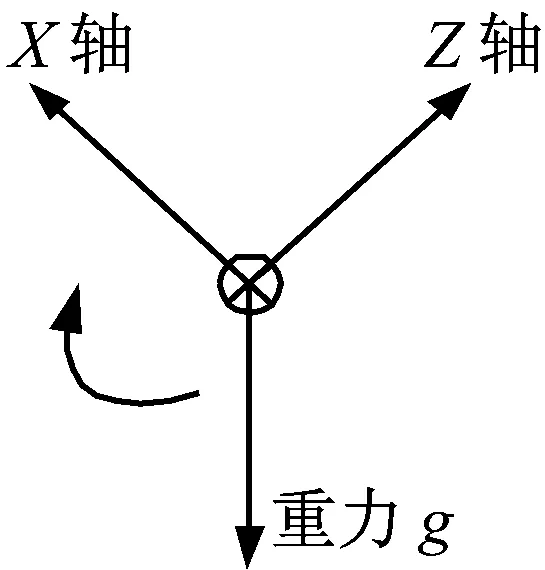
(b) 扭转图3 输电线扭转示意图Fig.3 Transmission line torsional movement

2.3 输电线路振动分析

综上分析，输电线路平动、扭转分析流程如图4所示，通过对连续采集的运动加速度、重力加速度变异度、相似性分析，计算振动幅度和频率系数(系数越大，说明振动幅度、频率越大)。

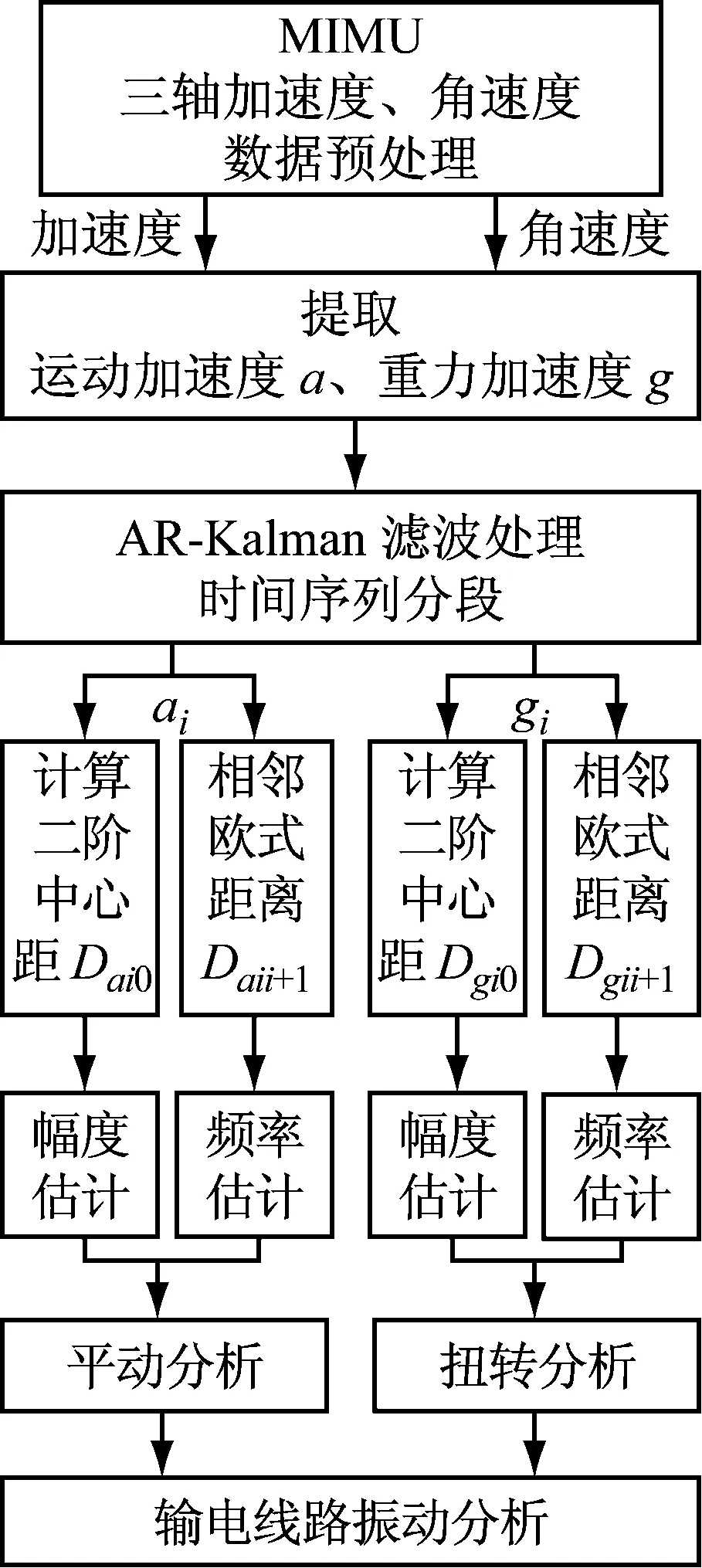
图4 输电线路振动分析流程图Fig.4 Analysis process of transmission line vibration

由前文分析知，振动幅度和频率系数的计算，依赖Damax、DEamax、Dgmax、DEgmax四个参数的确定。实际应用中，此四个参数的确定方法如下：①获取本地区输电线最大允许(或统计最大)平动或扭转频率，分别记为fa,fg；本地区输电线最大允许(或统计最大)振动角记为θ，最大平动振幅A=d·tan(θ)(d为MIMU安装点到绝缘子串悬挂点距离)；②振动台以振幅A，频率fa振动时采集MIMU加速度及角速度数据;摇摆台以频率fg，摇摆角θ摇摆运动时采集MIMU加速度及角速度数据；③通过前述流程计算相应的Dai0,Daii+1,Dgi0,Dgii+1多次重复上述过程，分别取Dai0,Daii+1,Dgi0,Dgii+1对应的均值作为Damax,DEamax,Dgmax,DEgmax。

以平动频率系数为横坐标、平动程度为纵坐标作幅频系数图，对应点称为平动点；以扭转频率系数为横坐标、扭转程度为纵坐标作幅-频系数图，对应点称为扭转点，通过分析本地区平动点、扭转点分布区域获取本地区输电线路振动特性，为后续振动阻尼器设计提供参数。

3 实验设计及结果分析

3.1 振动台模拟试验

为验证输电线路平动分析方法性能，特设计振动台振动模拟输电线路平动试验，将实验室设计的MIMU系统固定在振动台上，如图5所示。考虑安装及MIMU初始零偏误差，振动台静止时采集MIMU振动加速度作为初始数据段，振动台以不同振幅、频率振动时采集MIMU运动加速度作为振动数据段，Damax、DEamax分别设为振动台振幅/频率5 mm/150 Hz对应的振动加速度二阶中心距、相邻序列段欧式距离，数据分段数l取为30，经2.1节平动分析流程估计MIMU平动幅度及频率系数。

图5 MIMU振动试验Fig.5 Shaking-table test of MIMU

表1为振动台振动时设定的“振幅/频率”与由上述平动分析方法得到的平动“振幅系数/频率系数” 平均估计结果对比。由表1知，当振幅分别设定为1 mm、3 mm、5 mm时，计算的平动程度Da分别落在(0.17,0.21)、(0.59,0.62)、(0.92,1)区域，振幅与平动程度近似线性关系，可见本文方法计算的平动幅度系数对设定输入振幅有较好的跟随性；当振动台的输入频率依次为50 Hz、100 Hz、150 Hz时，计算的频率系数Fa依次属于(0.31,0.34)、(0.66,0.69)、(0.96,1)，频率系数与输入频率近似线性关系，可见基于欧氏距离度量的平动频率系数能够反映振动台输入频率变化规律。

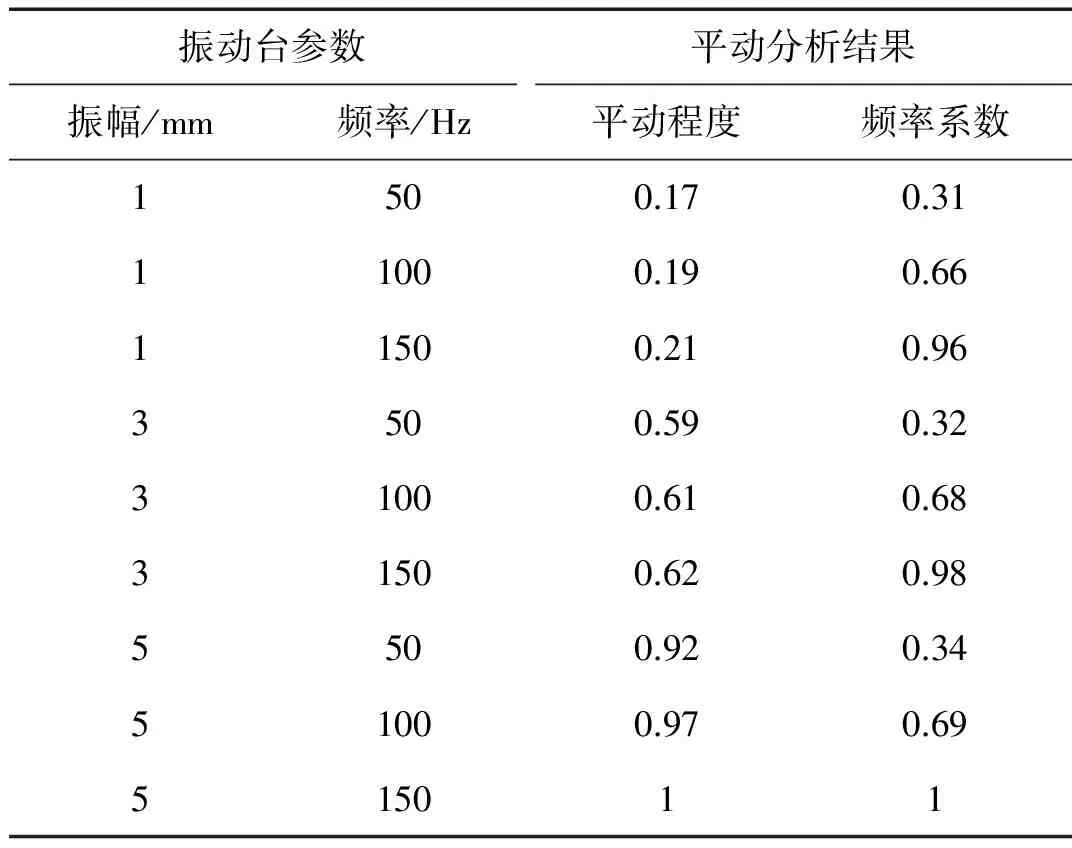
表1 MIMU振动台试验结果对比Tab.1 The shaking-table tests results of translationalamplitude and frequency

3.2 转台模拟试验

为验证输电线路扭转分析方法性能，特设计转台摇摆运动模拟输电线路扭转试验，将该MIMU系统固定在双轴转台上，如图6所示，MIMUZ轴垂直台面，调整台面水平且使MIMUX轴垂直于台面转轴。考虑安装误差及MIMU初始数据误差，转台静止下采集MIMU重力数据作为初始数据段，转台以不同角度、频率摇摆运动下采集MIMU重力数据作为扭转数据段，Dgmax、DEgmax分别取为转台摇摆角/频率5 deg/15 Hz对应的增广重力加速度二阶中心距、增广重力加速度相邻序列段欧式距离，数据分段数l取为30，按照2.2节扭转分析流程估计MIMU扭转幅度及频率。

图6 MIMU转台扭转试验Fig.6 Turntable test of MIMU

表2为转台做摇摆运动时设定的“摇摆角/频率”与由上述扭转分析方法得到的“扭转度/频率”估计结果对比。由表2结果知，当转台摇摆角分别设为小角1 deg、中角3 deg、大角5 deg时，计算的扭转程度Dg分别落在(0.18,0.22)、(0.58,0.61)、(0.93,1)区域，扭转程度与摇摆角近似线性，可见本文基于重力加速度二阶中心距度量的扭转幅度对输入摇摆角有较好的跟随性；当转台的输入频率依次为5 Hz、10 Hz、15 Hz时，计算的频率系数Fg依次属于(0.32,0.35)、(0.65,0.68)、(0.97,1)，频率系数近似正比输入频率，可见上述基于欧氏距离度量的扭转频率系数较好反映了转台输入频率变化规律。

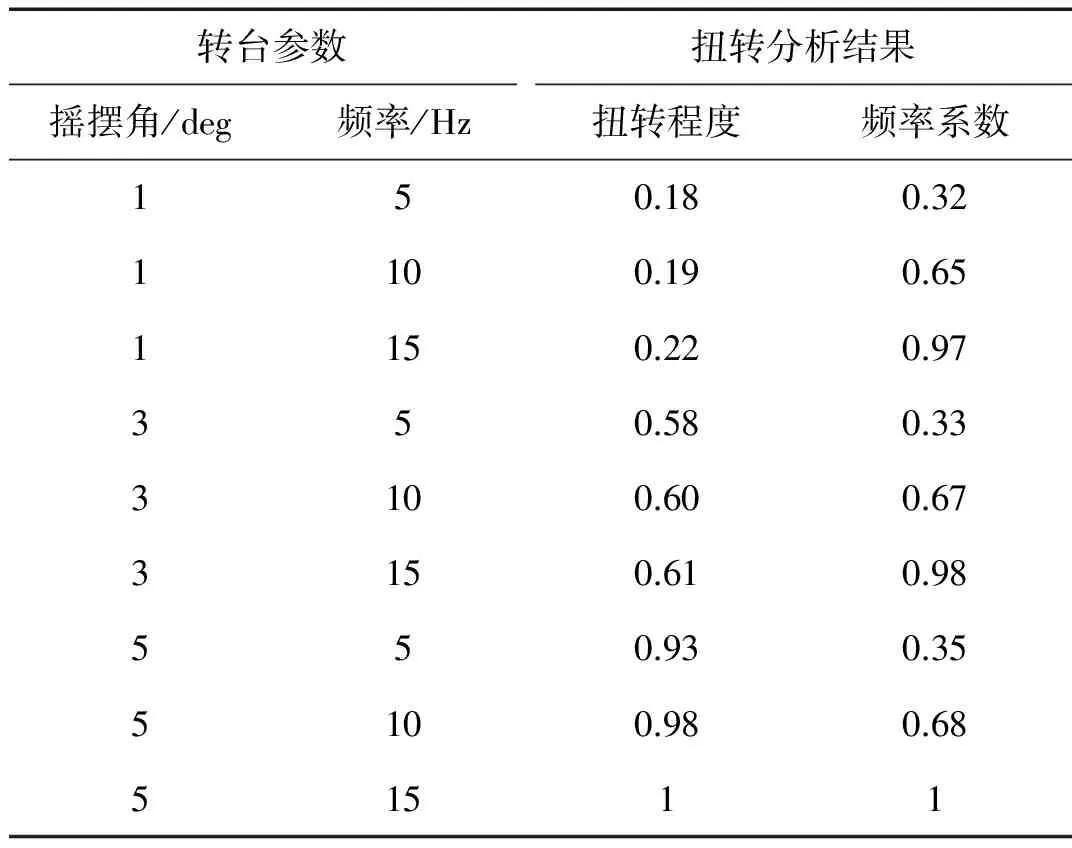
表2 MIMU转台试验结果对比Tab.2 The turntable tests results of torsional amplitudeand frequency

3.3 输电线路模拟试验

为进一步验证上述输电线路振动分析方法性能，按一定比例设计了输电线路模型，将MIMU系统按1.1节方案安装于模型，如图7所示。分别于2016-11-01、2016-11-11、2016-11-21各采集一组输电线路振动数据，考虑MIMU初始数据误差，输电线路静止时采集MIMU数据作为初始数据段，将采集的数据按2.3节分析流程处理，估计平动、扭转幅度及频率。Damax、DEamax、Dgmax、DEgmax取值同前，l取为30。

图7 输电线路模型试验Fig.7 Test of MIMU on transmission lines model

图8为采集并提取的某组输电线路平动加速度及估计的平动程度和频率系数。观察图8可知，各轴振动越大，平动程度也随之变大，说明各轴向平动程度对各轴向振动具有较好跟随性；各轴振动变化越剧烈，对应平动频率系数越大，平动频率系数对各轴平动变化剧烈度具有较好跟随性。

图9为采集的同组输电线路扭转时X,Z轴重力及估计的扭转程度和频率系数。观察图9，X轴、Z轴重力数据变化越大越快，说明扭转幅度频率也越大，对应扭转程度和扭转频率数值也越大，能够反映扭转变化规律。

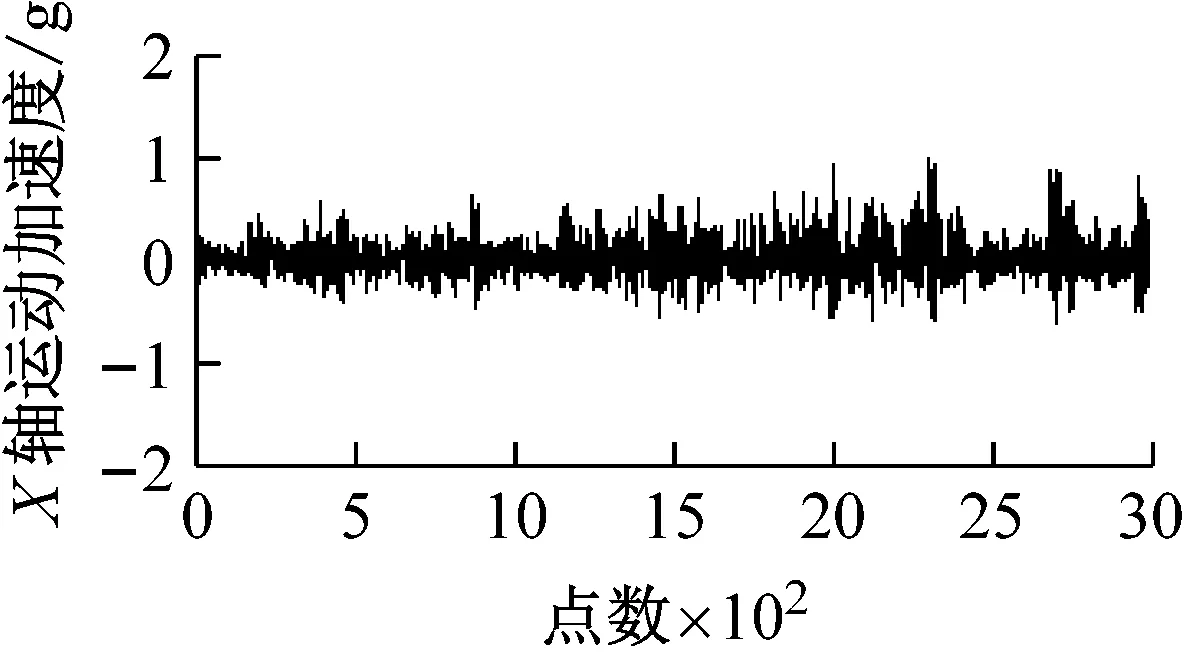
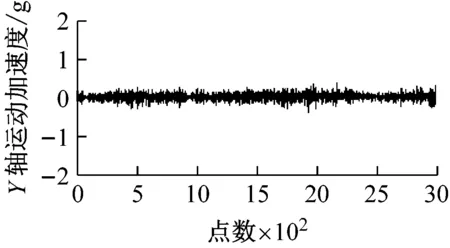
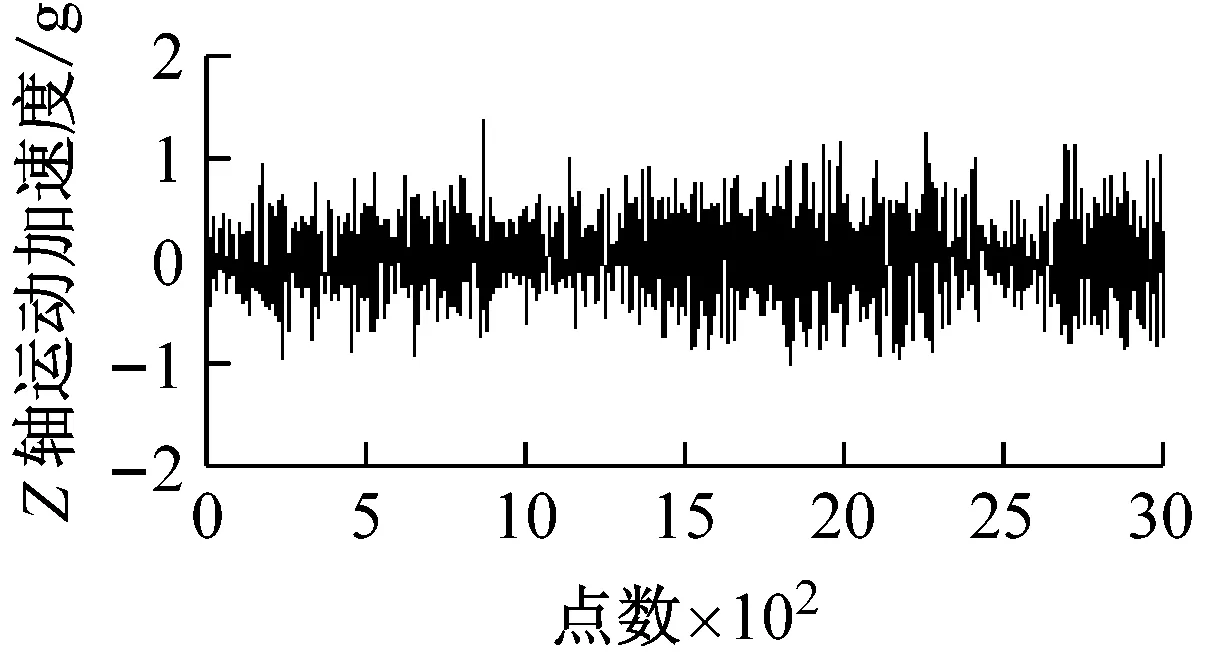
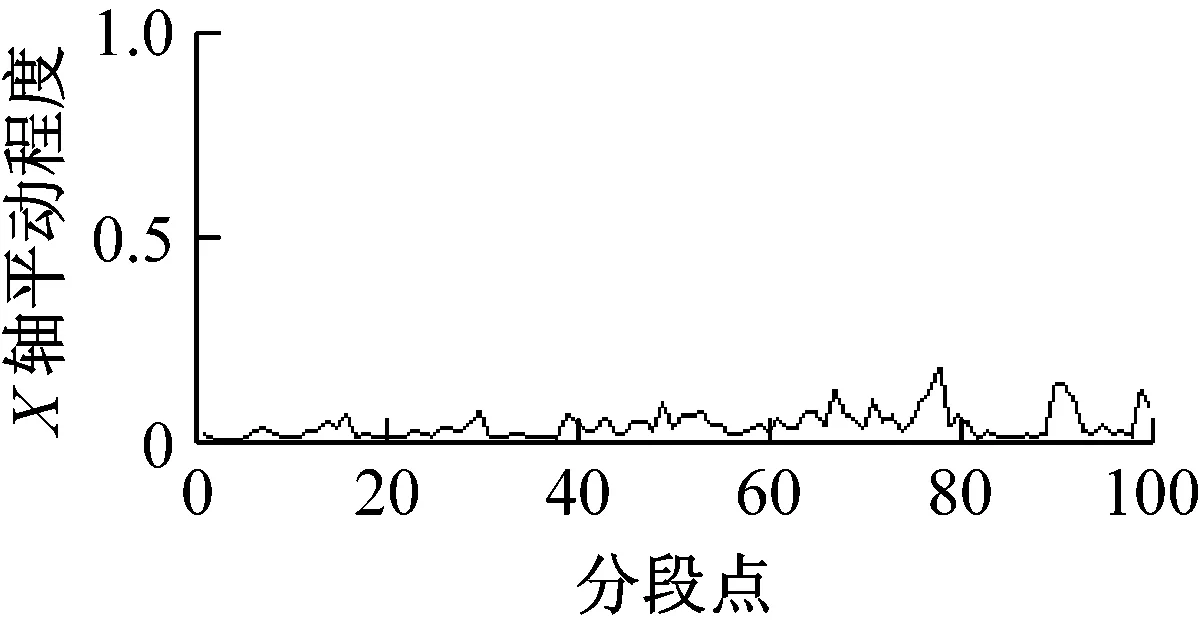
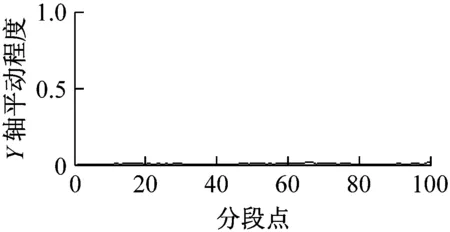
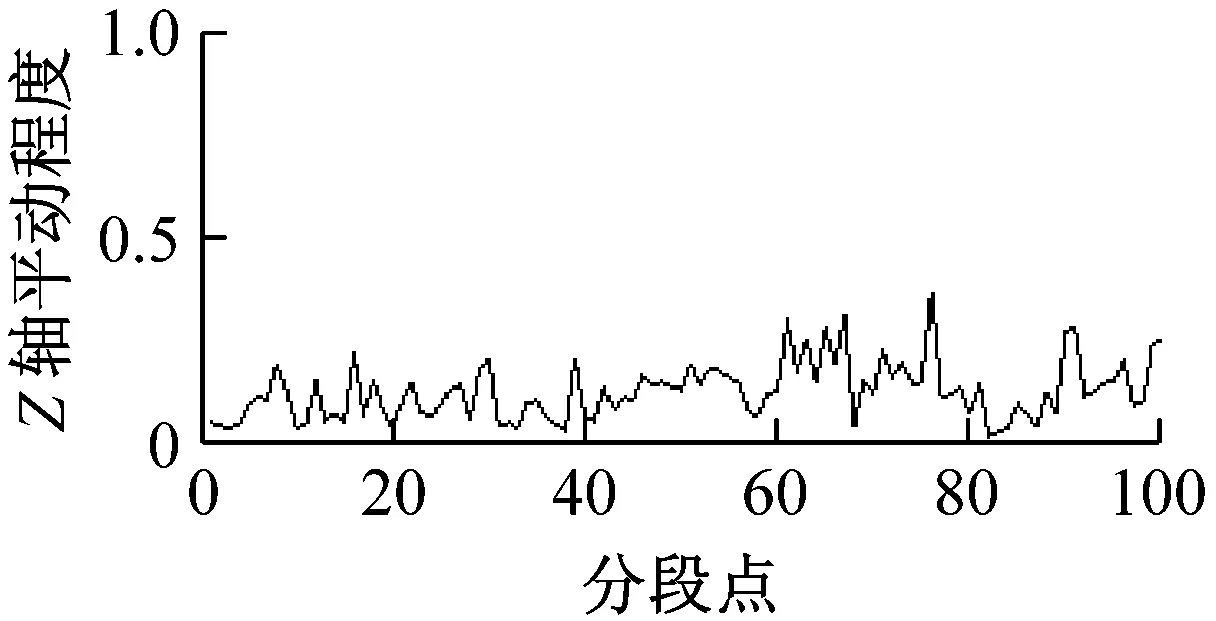
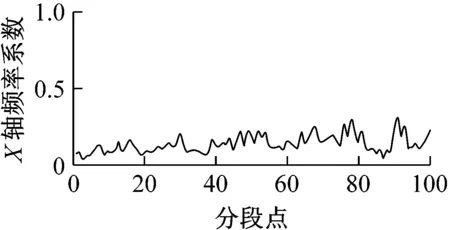
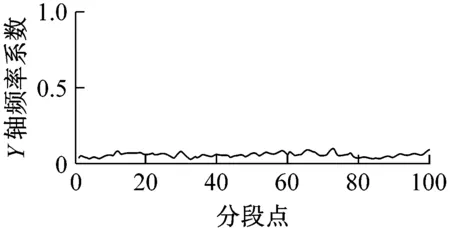
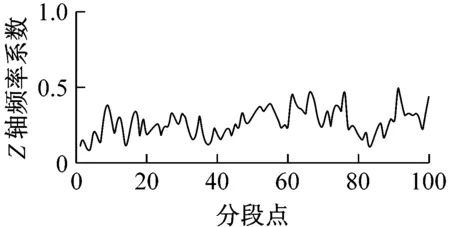
图8 输电线路模型平动分析Fig.8 Analysis of transmission line model translational movement

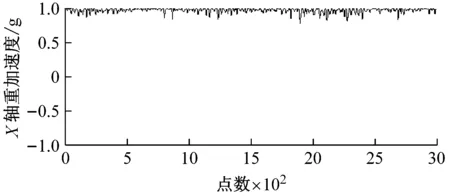
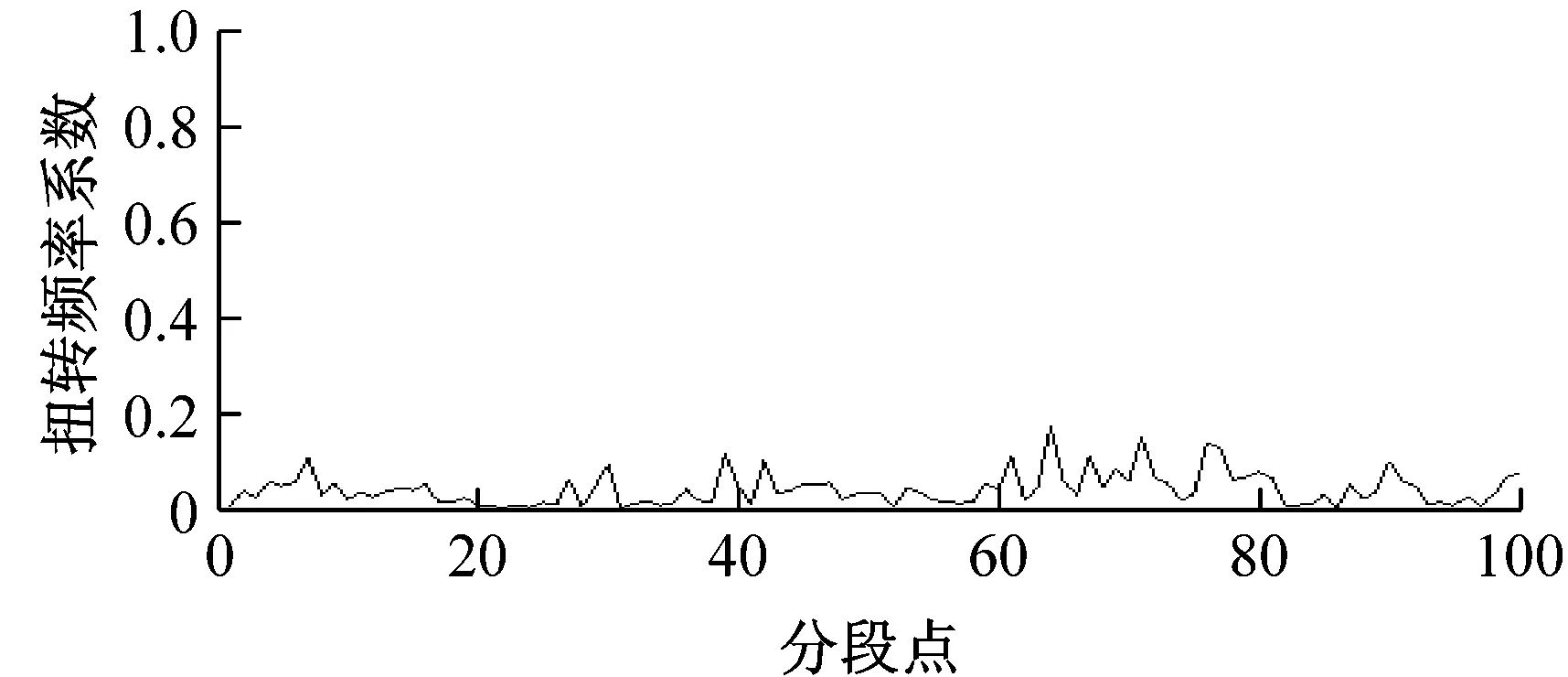
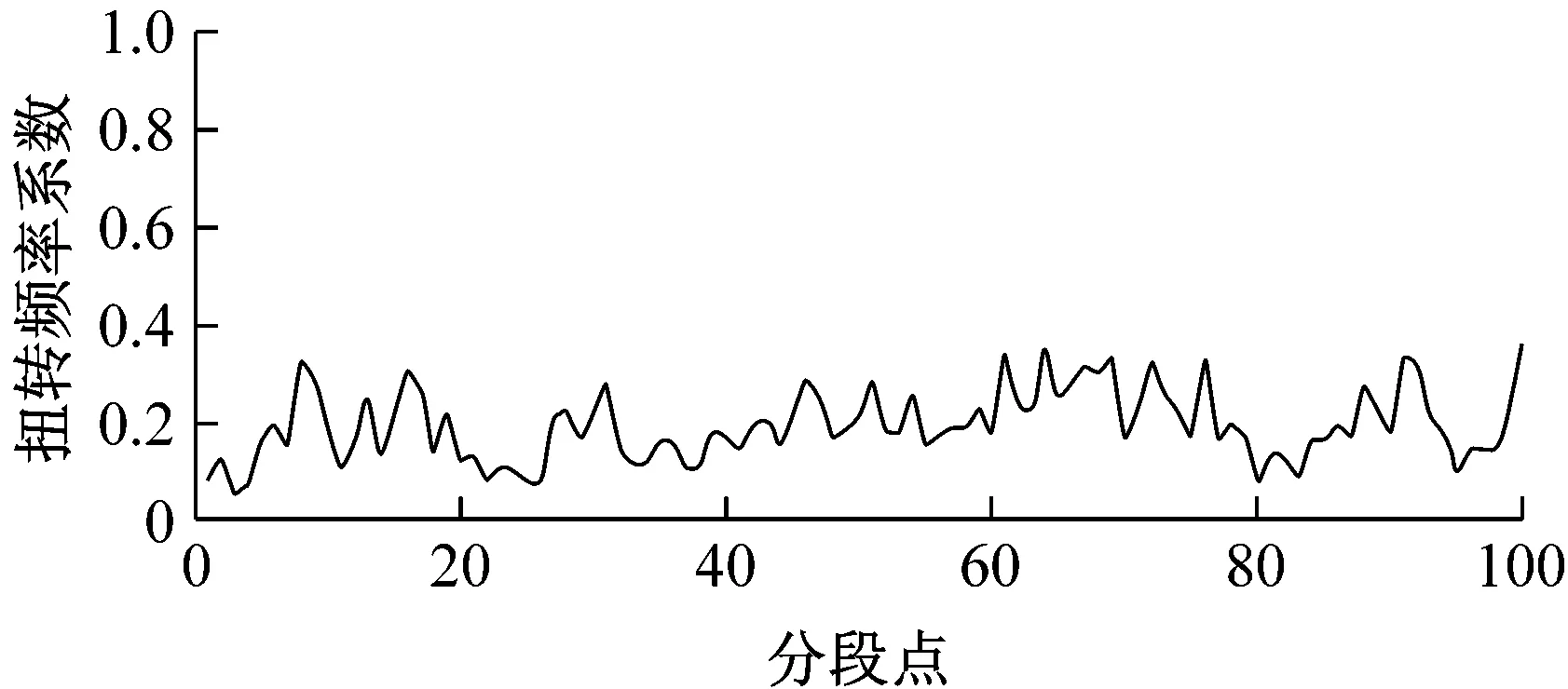
图9 输电线路模型扭转分析图Fig.9 Analysis of transmission line model torsional movement

图10为采集并提取的三组输电线路运动数据根据2.3节输电线路振动分析流程所绘振动幅度、频率综合分布图，从图中可发现，Z轴平动点分布于{(x,y),x∈(0,0.4),y∈(0,0.2)}区域，X轴平动点分布于{(x,y),x∈(0,0.3),y∈(0,0.1)}区域，Y轴平动不明显，说明平动程度和频率较小；扭转点集中于{(x,y),x∈(0,0.1),y∈(0,0.02)}区域，说明扭转程度及频率很小，综上可知，该段时间内输电线路振动程度较小。连续长期监测输电线路振动并计算振动(扭转)程度和频率，根据平动(扭转)程度与幅度(摇摆角)、频率系数与频率正比关系，结合设定的最大幅度(扭转角度)及频率可获知本地区输电线路振动特点，为后续振动阻尼器设计，提供参数依据。

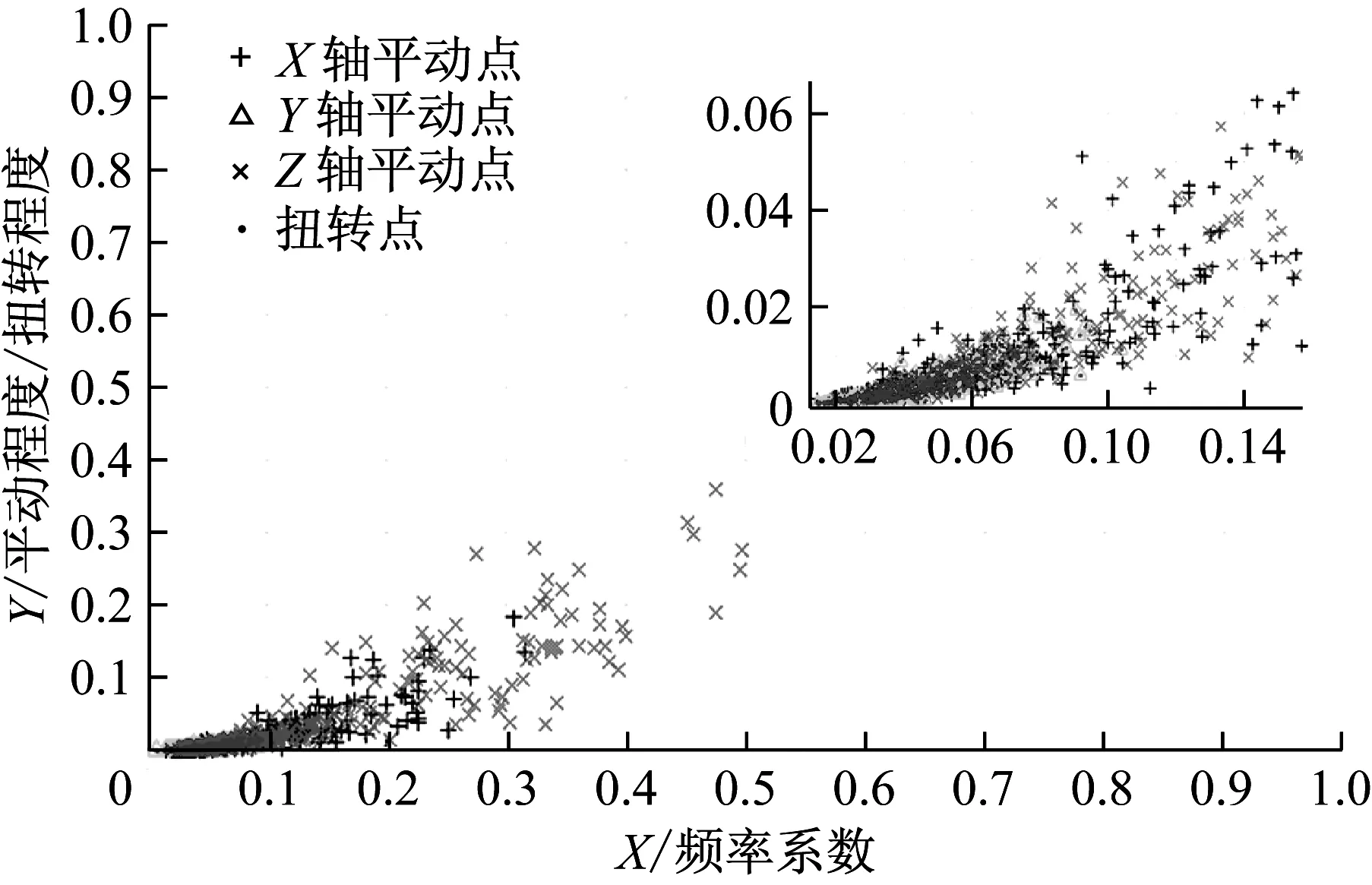
图10 振动幅度频率综合分布图Fig.10 Comprehensive distribution map about the vibration amplitude-frequency of transmission line

4 结 论

针对通过多点MIMU解算导线运动轨迹来分析本地区输电线路振动特点精度不高且难以实现长期监测，提出一种惯性测量参数的时间序列分段模式的输电线路振动分析方法。设计了一种MIMU测量节点并采用一定长度的弹性杆进行信号物理放大和防磁干扰，通过对MIMU时间序列变异度分析和相似性度量，预测输电线路平动、扭转程度及频率，进而评估输电线路运动异常程度。最后设计了振动台、转台模拟平动、扭转试验和输电线路模型实验，采集不同平动、扭转程度及频率时的MIMU信号，实验结果表明，处理数据结果能够反映输电线路平动和扭转变化规律，说明输电线路运动分析方法是有效的，且实施方案易行，计算简单，无累计误差，工程实用性较强, 可以为实现长期监测本地区输电线路振动幅度和频率提供参考，以进一步为输电线路振动阻尼控制器设计提供参数。

参 考 文 献

[1] 叶志雄. 输电线微风振动及次档距振荡控制研究[D].武汉:华中科技大学,2009.

[2] 张帆,熊兰,刘钰．基于加速度传感器的输电线舞动监测系统[J]．电测与仪表,2009,46(1): 30-33．

ZHANG Fan, XIONG Lan, LIU Yu. Transmission lines galloping monitoring system based on accelerometer sensors[J]. Rlectrical Measurement &lnstrumentatinn, 2009, 46(1): 30-33．

[3] 黄官宝,黄新波,赵雪松,等．输电线路导线舞动在线监测系统设计[J]. 南方电网技术,2009, 3(4):85-89.

HUANG Guanbao, HUANG Xinbo, ZHAO Xuesong, et al. On-line monitoring system design on transmission line galloping[J]. Southern Power System Technology, 2009, 3(4): 85-89.

[4] 王有元,任欢,杜林. 输电线路导线舞动轨迹监测分析[J]．高电压技术,2010,36(5): 1113-1118．

WANG Youyuan, REN Huan, DU Lin.Analysis on conductor galloping track monitoring of transmission line[J]. High Voltage Engineering, 2010,36(5): 1113-1118.

[5] 黄新波,赵隆,周柯宏,等. 采用惯性传感器的输电导线舞动监测系统[J]．高电压技术,2014,40(5): 1312-1319．

HUANG Xinbo, ZHAO Long, ZHOU Kehong, et al. Conductor galloping monitoring system based on inertial sensor for tansmission lines[J]. High Voltage Engineering,2014,40(5): 1312-1319.

[6] 邵颖彪,杨晓辉,郭薇,等. 基于九轴传感器监测导线舞动的研究方法[J]. 智能电网,2015, 5(1): 1-8.

SHAO Yingbiao, YANG Xiaohui, GUO Wei, et al. Monitoring galloping of transmission lines based on nine-axis sensors[J].Smart Grid, 2015, 5(1): 1-8.

[7] 晏致涛,李正良,杨振华．基于结点6自由度的输电线舞动有限元分析[J]．振动与冲击,2011, 30(8): 112-117．

YAN Zhitao, LI Zhengliang, YANG Zhenhua. Finite element modeling of transmission line galloping based on 6-DOFs nodes[J].Journal of Vibration and Shock,2011, 30(8): 112-117．

[8] 黄新波,赵隆,舒佳,等. 输电线路导线微风振动在线监测技术[J]. 高电压技术,2012,38(8):1863-1870.

HUANG Xinbo, ZHAO Long, SHU Jia, et al. Online monitoring conductor aeolian vibration of transmission lines[J]. High Voltage Engineering, 2012, 38(8):1863-1870.

[9] 王宝成. 油气弹簧阻尼器在输电线路防舞动的应用[J]. 内蒙古电力技术,2011,29(3):73-75.

WANG Baocheng. Application of oil vapor spring-dampers in prevention of power transmission line waving[J]. Inner Mongolia Electric Power,2011,29(3):73-75.

[10] LANGLOIS S, LEGERON F. Prediction of aeolian vibration on transmission-line conductors using a nonlinear time history model—Part II: conductor and damper model[J]. IEEE Transactions on Power Delivery, 2014, 29(3):1168-1175.

[11] SAADABAD N A, MORADI H, VOSSOUGHI G. Semi-active control of forced oscillations in power transmission lines via optimum tuneable vibration absorbers: with review on linear dynamic aspects[J]. International Journal of Mechanical Sciences, 2014, 87(4):163-178.

[12] LEE J K, PARK E J, ROBINOVITCH S N. Estimation of attitude and external acceleration using inertial sensor measurement during various dynamic conditions[J]. IEEE Transactions on Instrumentation and Measurement, 2012,61(8):2262-2273.

[13] ALAM M, ROHAC J. Adaptive data filtering of inertial sensors with variable bandwidth[J]. Sensors, 2015,15(2):3282-3298.

[14] 杜永峰,李万润,李慧,等. 基于时间序列分析的结构损伤识别[J]. 振动与冲击,2012, 31(12):108-111.

DU Yongfeng, LI Wanrun, LI Hui, et al. Structural damage identification based on time series analysis[J]. Journal of Vibration and Shock, 2012, 31(12):108-111.

[15] 刁延松,任红. 基于AR模型和因子分析的结构损伤预警研究[J]. 振动与冲击,2014, 33(18):115-119.

DIAO Yansong, REN Hong. Structural damage early warning based on AR model and factor analysis[J]. Journal of Vibration and Shock, 2014,33(18):115-119.

[16] YANG Jinxian, LI Zhipeng. Deformation prediction based on MIMU signal[J]. Journal of Computational Information Systems,2014,11(8): 6741-6751.