基于两种接触模型的柔性体间多次微碰撞问题研究

王检耀， 刘铸永， 洪嘉振(上海交通大学 工程力学系，上海 200240)

工程中经常会发生结构间的多次碰撞，如航天器对接时导向板之间的接触碰撞[1]；高速列车受电弓/接触网间的碰撞振动[2]；连杆机构的铰间隙引起的反复冲撞[3]。多次碰撞会激发柔性体的高频振动，影响机械系统的运行精度，而且往复碰撞对结构强度的破坏甚至高于单次高强度的碰撞[4]。

多次碰撞不仅指肉眼或听觉能分辨的往复的宏观碰撞。在一次短暂的宏观的碰撞过程中，由于结构的弹性振动与碰撞发生相互作用，很有可能会发生多次间歇性“接触-分离-再接触”的微碰撞现象。Stoianovici等[5-6]在碰撞实验研究中捕捉到了一次宏观碰撞中的多次微碰撞过程。在碰撞问题的理论研究中，刚体碰撞理论[7-8]忽略了弹性振动，因此无法表现出多次微碰撞现象；高玉华等[9-10]利用应力波理论解析求解了柔性杆纵向碰撞问题，并解释了多次微碰撞现象；对于柔性梁、板等结构的碰撞问题，段玥晨等[11]用假设模态法求解了柔性梁的多次碰撞问题，刘锦阳等[12]用动态子结构方法求解了太阳帆板锁定时的撞击问题，也有二次或多次微碰撞现象发生。对于复杂的三维结构的碰撞问题，更通用的做法则是用有限元方法求解。在有限元方法中，处理接触碰撞的方法有两种：接触力元方法[13-14]和接触约束方法[15]。接触力元方法将接触作用视为弹簧阻尼器力元，根据物体间的嵌入量直接由相应函数给出接触力，又称为罚函数法(Penalty Method，PM)。接触约束方法将接触作用视为接触约束，接触约束方程与带Lagrange乘子的动力学方程联立求得接触力，又称为Lagrange 乘子法或附加约束法(Lagrangian Method，LM)。

本文基于有限元法的三维实体单元模型，分别采用罚函数法和附加约束法对柔性结构间一次碰撞产生的多次微碰撞过程进行研究。利用点-面接触对接触域进行离散，分别推导了罚函数法和附加约束法的动力学方程，对杆-梁多次微碰撞问题进行仿真，研究了接触刚度、网格尺寸等参数对多次微碰撞过程中碰撞次数、碰撞力峰值和碰撞时间的影响。

1 接触域处理

在有限元方法中，为了精确描述接触的作用，对接触进行细致的空间离散化，在离散后的接触域上形成多个接触对，而接触力元或约束施加在各个接触对上。碰撞过程中，接触点对的形成与分离表现了接触区域的时变过程。最广泛使用的接触域离散形式为点-面接触对(node to segment)。如图1所示，把撞击物体称为从物体(slave body)，被撞击物体称为主物体(master body)，从物体上的一点i与主物体单元表面si上的最近投影点i′构成接触对。接触对间距矢量有如下形式

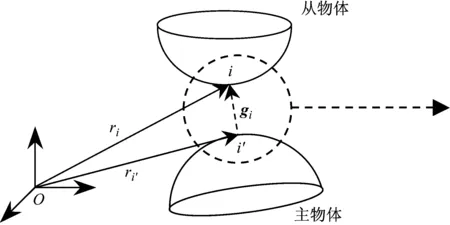
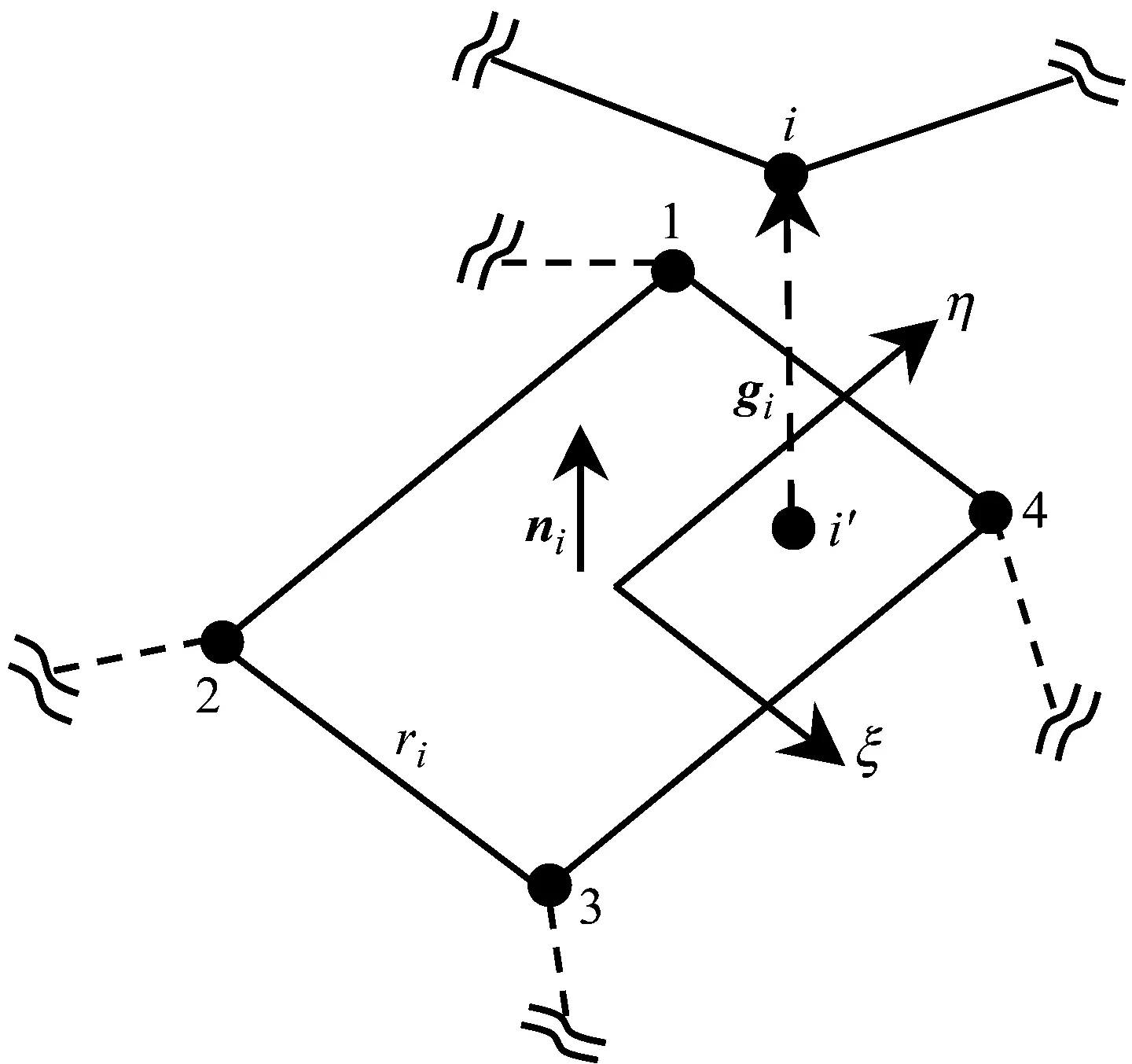
图1 点-面接触对Fig.1 A node-to-segment contact pair

gi=ri-ri′=ri0-ri′0+ui-ui′

(1)

式中：ri和ri′分别表示节点i和i′在惯性坐标系下位置；ui和ui′分别表示表示节点i和i′的位移。接触点间的法向距离可以写为

gNi=ni·gi

(2)

式中:ni主物体表面si上点i′位置的法向矢量。当gNi>0，表示没有碰撞发生；当gNi=0，表示碰撞刚刚开始；当gNi<0，则表示接触点对之间有互相穿透。

2 接触作用的力学模型

系统中物体的相互作用有两种力学模型：力元和约束。相应地，目前处理接触/碰撞过程的方法有两种：接触力元方法和接触约束方法。接触力元方法将接触作用视为弹簧阻尼器力元，力元根据接触点对嵌入量直接由相应模型给出接触力，又称为罚函数法。接触约束方法将接触作用视为接触约束，接触约束方程与带Lagrange乘子的动力学方程形成封闭的方程组，该方法又称附加约束法。

2.1 罚函数方法

罚函数方法把碰撞力作为力元处理，检测到接触发生时，在接触域内的各接触对间添加相应的接触力元，直至分离。当碰撞发生时，从物体上的点i将嵌入主物体表面si，嵌入量δi=-gNi。罚函数法中给出嵌入与碰撞力的关系，从而通过嵌入量直接计算出碰撞力。罚函数法将接触作用视为弹簧力元，接触力大小表达为

Fi=kδi

(3)

式中:k为弹簧刚度，由主物体上si所在单元的体积模量Ki、单元体积Vi、接触面面积Ai计算得到

(4)

式中:fs称为罚因子，用于调节接触刚度。

有限元中，接触力需要分布到单元相关节点上。对于从物体接触点i，节点力为Fi=kδini，对于主物体接触单元表面，由节点j(j=1,2,3,4)组成，接触作用的等效节点力表示为

(5)

式中:ξi′,ηi′是i′在表面si的局部坐标,Nj为插值函数，表示为

(6)

接触对i-si的接触力可以写为

(7)

从而在碰撞期间，系统的动力学方程为

(8)

式中:M为质量阵;u为位移矢量阵;Fint和Fext分别为内力阵和外力阵;Fc为所有接触点对的接触力的组集。

罚函数方法的优点在于不需要求解约束方程，且动力学方程的维数固定，不随接触状态改变。其不足之处在于，需要人为选取合适的罚因子，且没有统一的选取准则，需要根据经验多次试算才能获得可靠结果。

2.2 附加约束方法

附加约束方法中，检测到接触发生时，根据互不穿透的约束条件，施加相应的约束方程。接触约束方程与带Lagrange乘子的动力学方程联立求解运动学变量和接触力。当从物体节点i接触到主物体表面si时，位置形式的约束方程可以写为

Φi(u)=ni·gi=0

(9)

把式(1)和式(6)代入式(9)中，得到：

(10)

当更多的节点进入接触时，所有的接触约束方程可以组集为

(11)

式中:m为接触点对数。那么系统的动力学方程可写为

(12)

式中:Φu是接触约束矩阵的雅可比矩阵;λ是相应的Lagrange乘子。

为了求解式(11)，对其二阶求到后，得到加速度形式的约束方程

(13)

(14)

不同于罚函数方法，附加约束方法的优点在于不需要人为选取刚度等参数，并且互不嵌入的约束条件是严格满足的。但是附加约束法中的约束方程增加了方程维数，并且随接触状态改变，另外微分-代数方程的数值求解也更加困难。

3 算 例

如图2所示，为一柔性球头圆柱杆撞击两端固支方形截面横梁的三维有限元模型。分别使用罚函数方法和附加约束方法对该碰撞过程进行数值仿真。碰撞物体的几何和材料参数列于表1中。

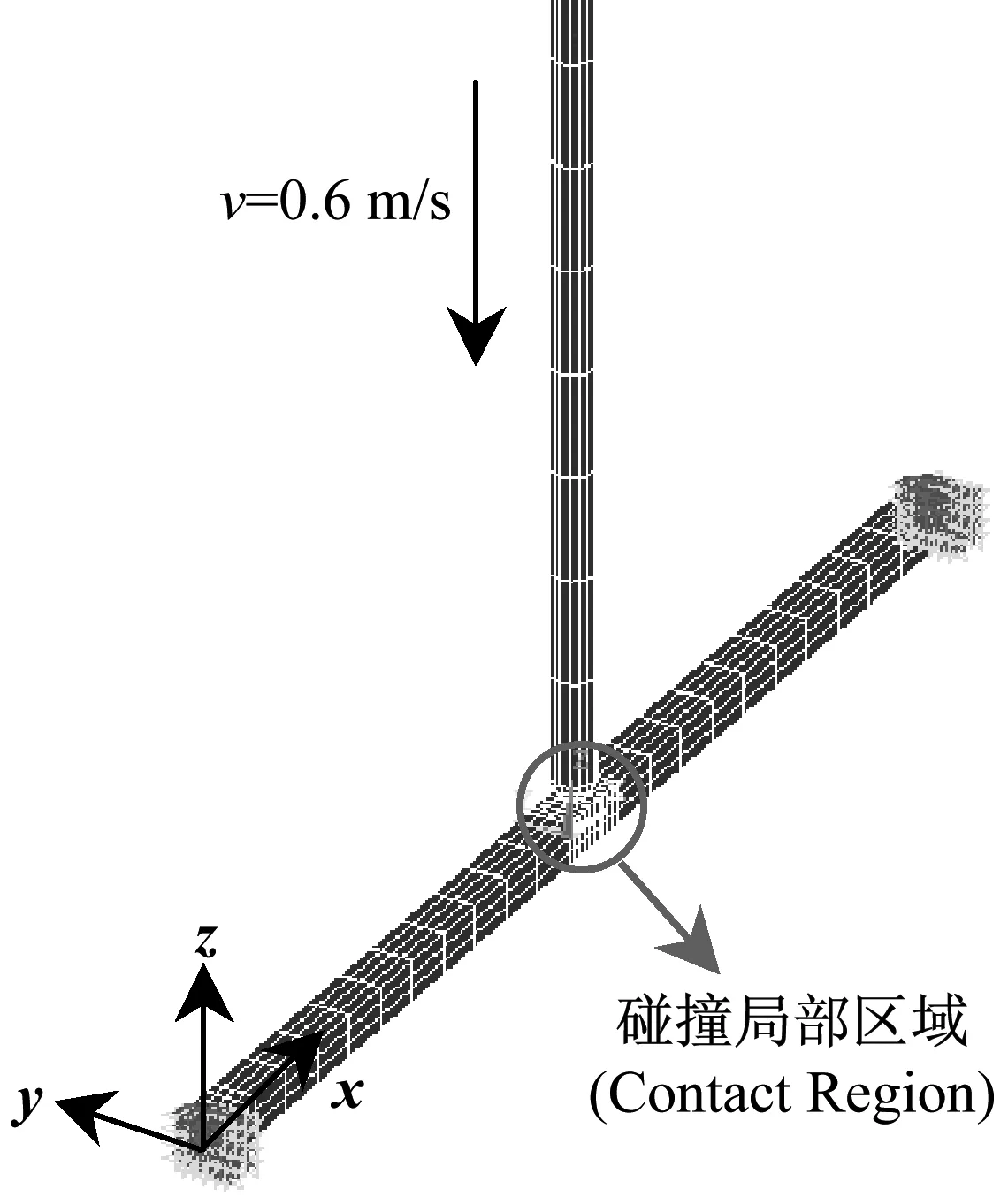
图2 杆-梁撞击的三维有限元模型Fig.2 FE model of the rod-beam impact case

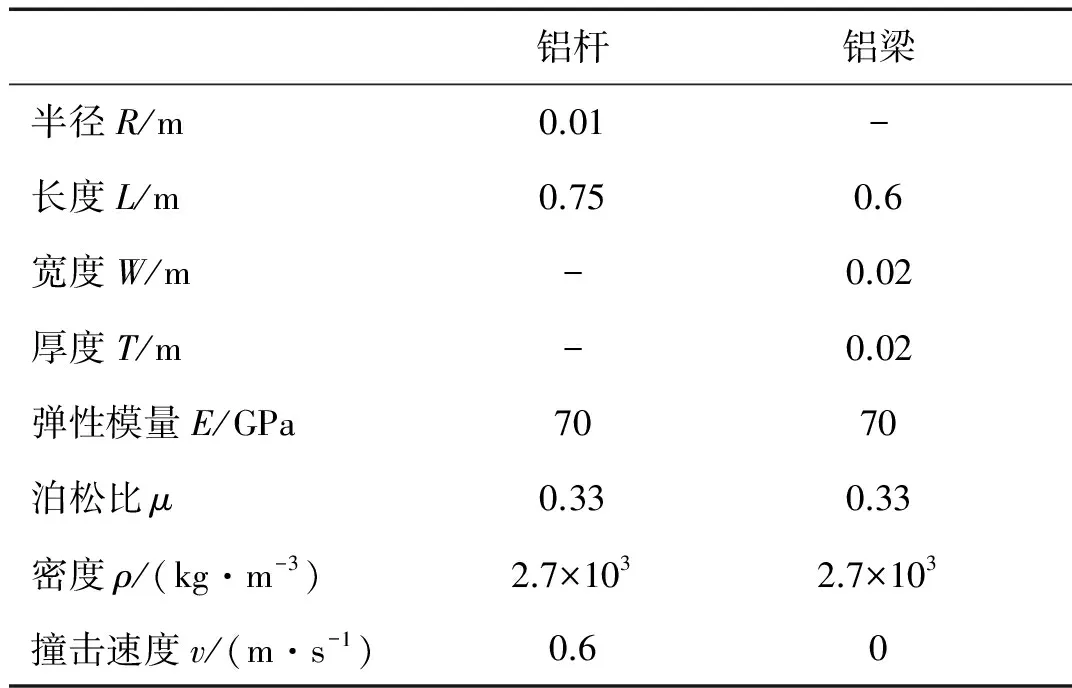
表1 几何与材料参数Tab.1 Geometrical and material parameters

3.1 罚因子的影响

罚函数方法中，罚因子的选取决定了接触刚度的大小。为了研究罚因子的取值对碰撞结果的影响，分别对不同的罚因子进行仿真。不同罚因子下的碰撞力随时间的历程如图3所示。当罚因子取值为0.01时，由于过小的接触刚度导致碰撞时间明显过长，并且碰撞力的峰值偏小。随着罚因子值的增加，碰撞力和碰撞力时间逐渐收敛。罚因子取值0.5和1时，结果已经几乎一致，此时的罚因子是合适的，当继续增大罚因子时，有可能因为过大的接触刚度发生数值不稳定。另外可以看到，当罚因子取值为0.01和0.1时，整个过程中碰撞力没有过零，表示整个过程中接触物体没有分离；而当罚因子取值为0.5和1时，则可以看到碰撞力有多次过零。可以看到罚因子的选取不仅影响碰撞力峰值及碰撞持续时间，还影响碰撞过程的碰撞次数。因此，罚函数方法必须通过试算获得合适的罚因子。

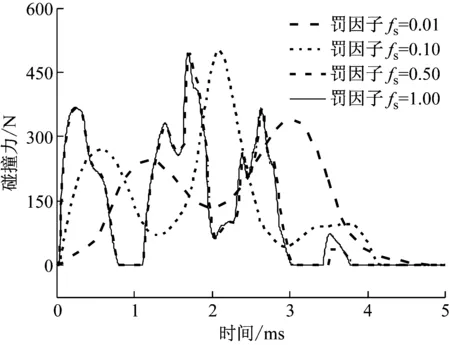
图3 不同罚因子的碰撞力结果Fig.3 Contact force with different penalty factors

3.2 网格尺寸的影响

在使用有限元方法的接触碰撞问题中，空间离散的网格尺寸对于仿真结果有很大的影响。在远离碰撞局部的区域，网格尺寸应该能够保证弹性波的传播特征；在碰撞局部区域，则应使用更细密的网格来反映局部高应力的分布以及接触域随时间的演化历程。本节将研究碰撞局部的网格尺寸对罚函数法和附加约束法的影响。

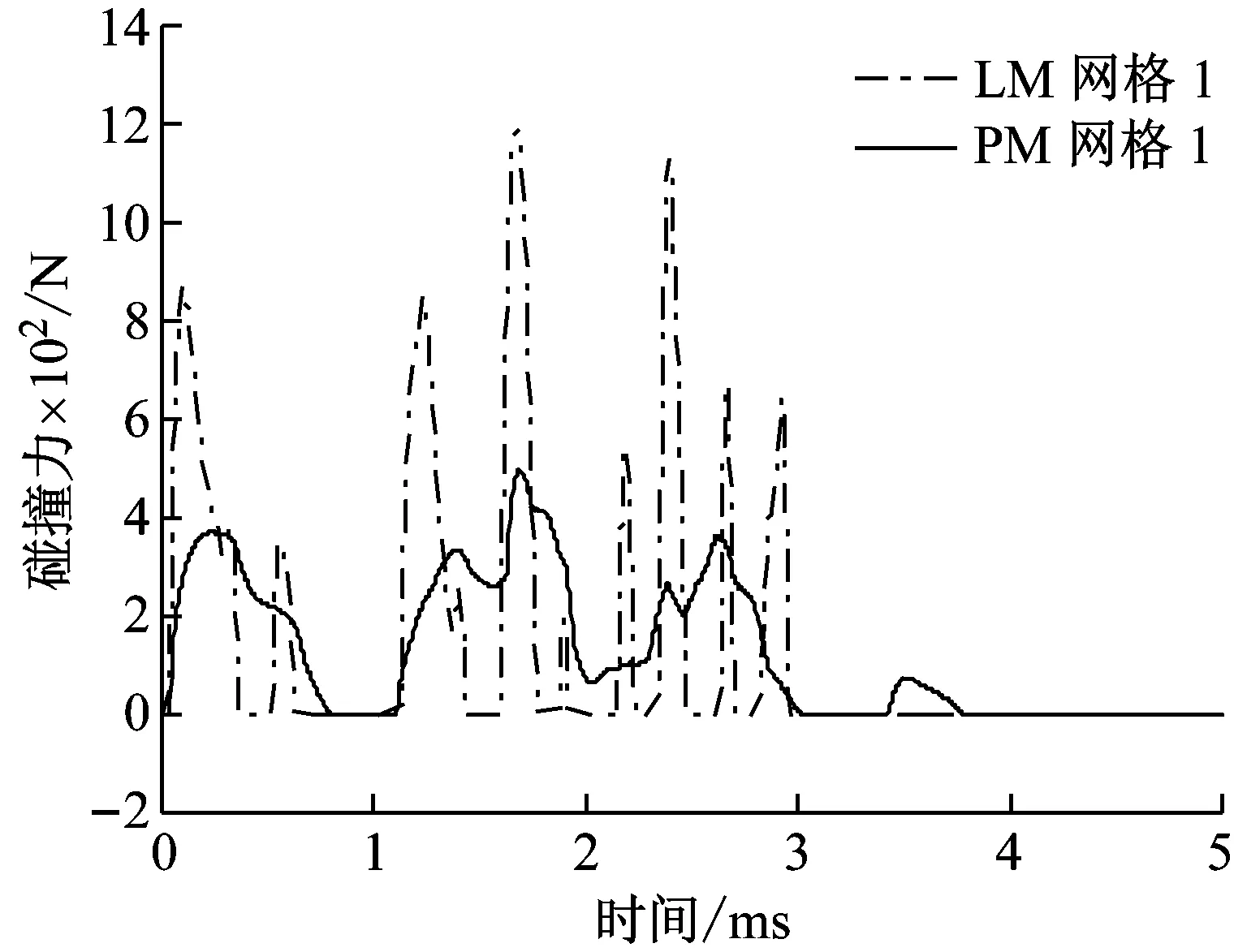
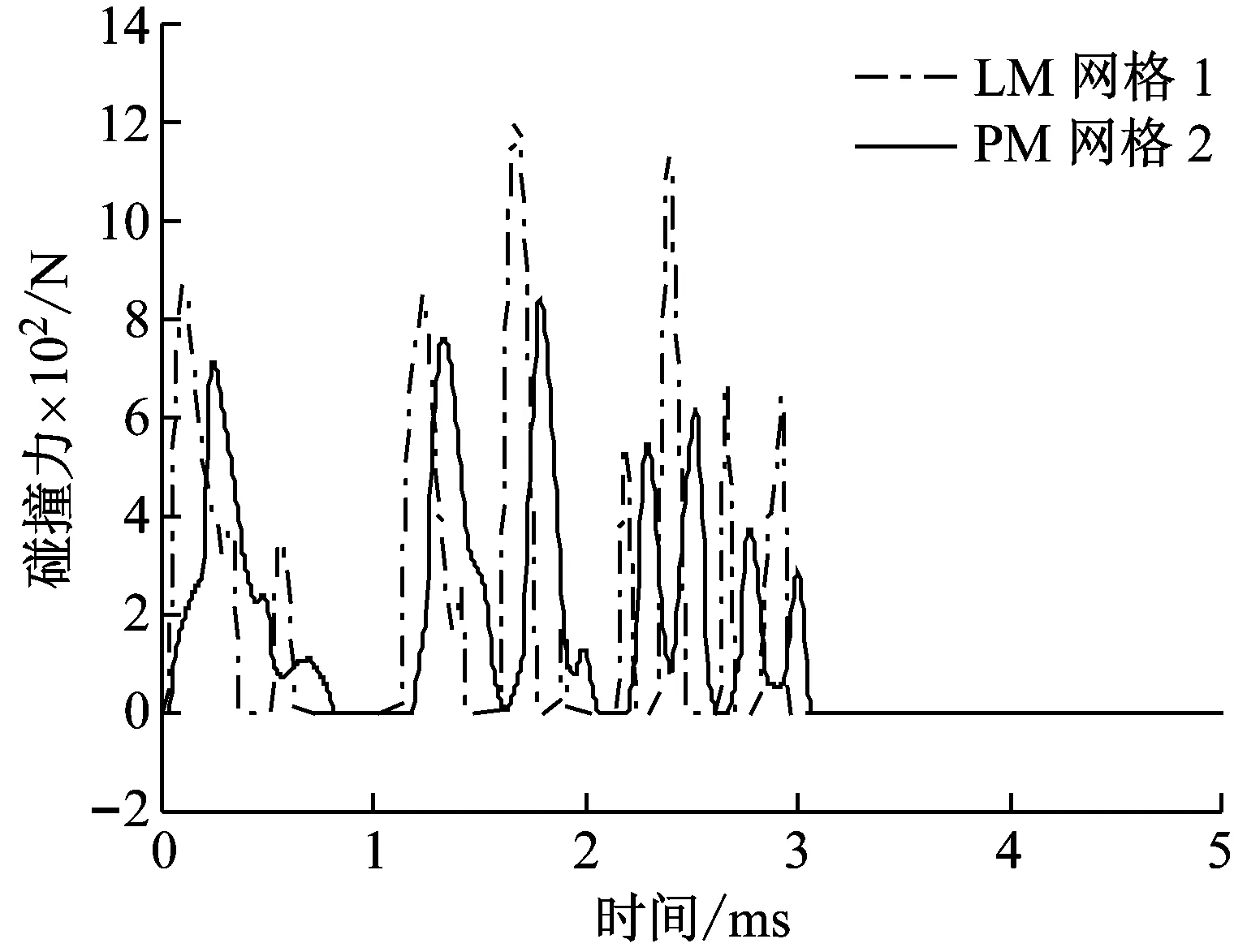
对于罚函数方法，如图2所示，对碰撞局部区域用4种不同尺寸网格离散，而对于每一种网格，类似于3.1中的步骤，均需要重新选取合适的罚因子，同时网格尺寸越小，积分的步长也越小。网格尺寸信息及每种网格下的罚因子及时间步长信息均列于表2中。在每种网格下罚函数法计算得到的碰撞力曲线如图4所示，可以看出，罚函数法的结果非常依赖于碰撞局部的网格尺寸，随着网格变细，其结果逐步收敛于“精确解”。而对于附加约束方法，我们计算其在网格1下的结果，同样作于图4中，将它与罚函数方法在4种网格下的结果进行比较。我们发现附加约束法在网格1下的结果已经与罚函数法在网格4下的“精确解”吻合。因此，可以认为罚函数法的结果精度更依赖于网格尺寸。由于罚函数法比附加约束法需要更细密的网格，因此在数值仿真中，罚函数法带来更庞大的自由度并且需要更多的积分步数。两者在计算耗时上的对比如表3所示，附加约束法在计算效率上有一定优势。总结来说，罚函数方法非常依赖于接触局部的网格尺寸，只有当网格尺寸充分小时，才能预测出正确的多次微碰撞过程，包括碰撞力峰值、碰撞时间和碰撞次数。而附加约束方法在较粗的网格下已经能获得比较理想的结果。

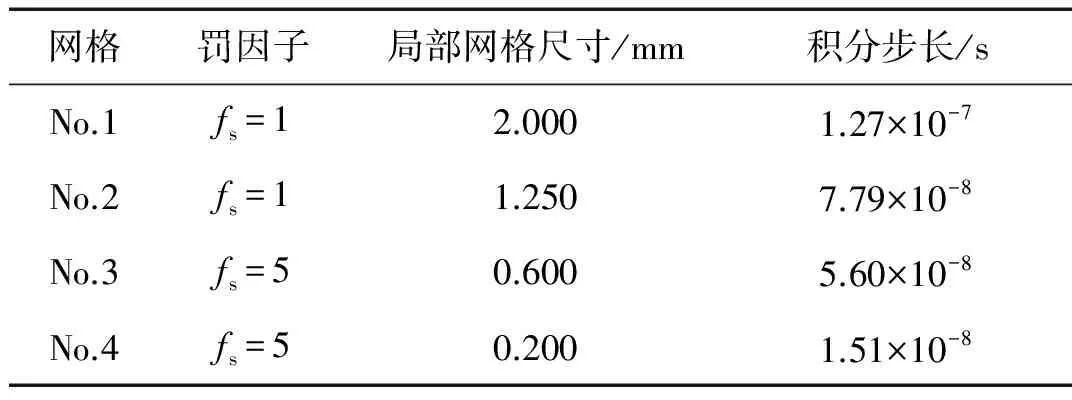
表2 罚函数法的参数Tab.2 Parameters of penalty method

(a)

(b)

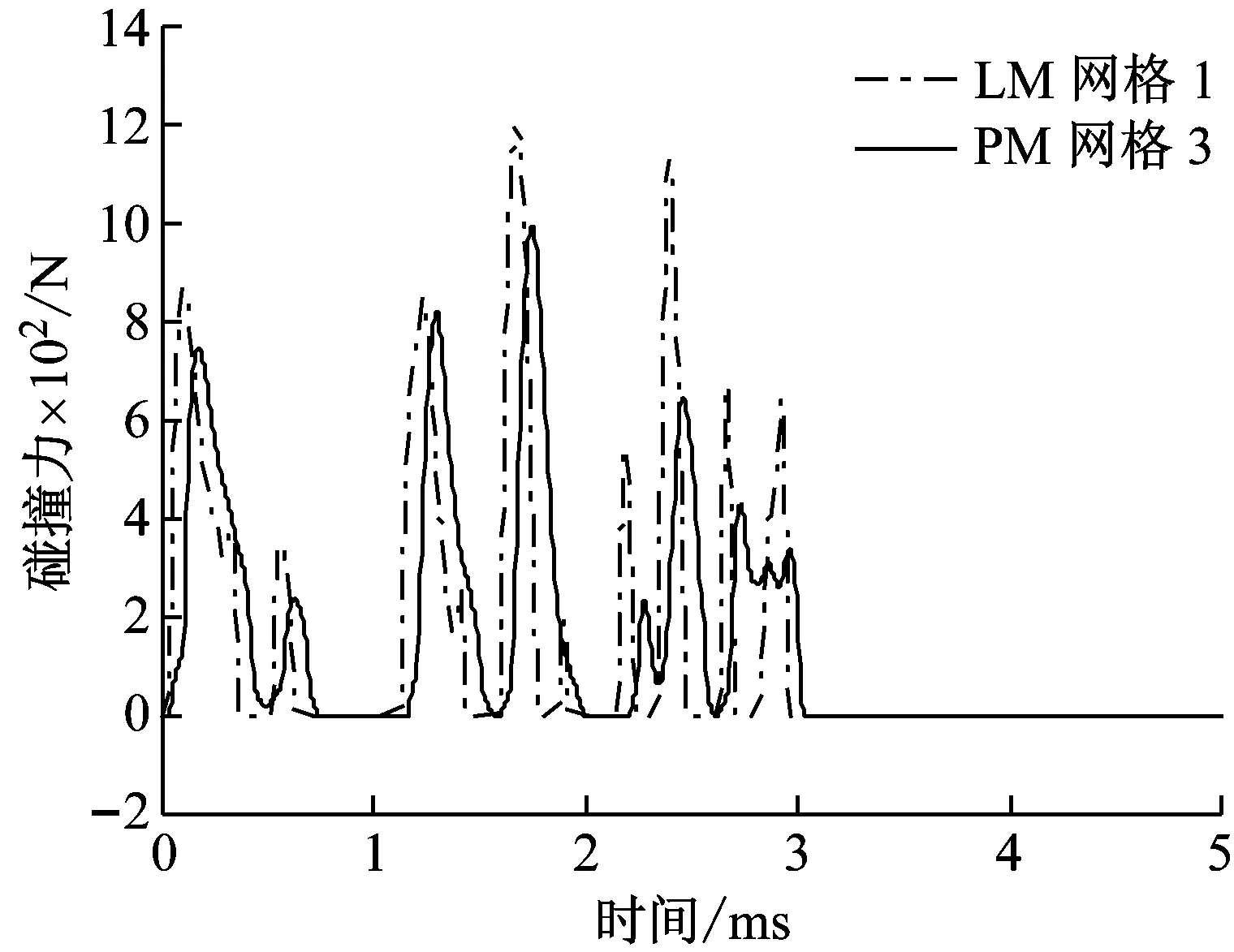
(c)

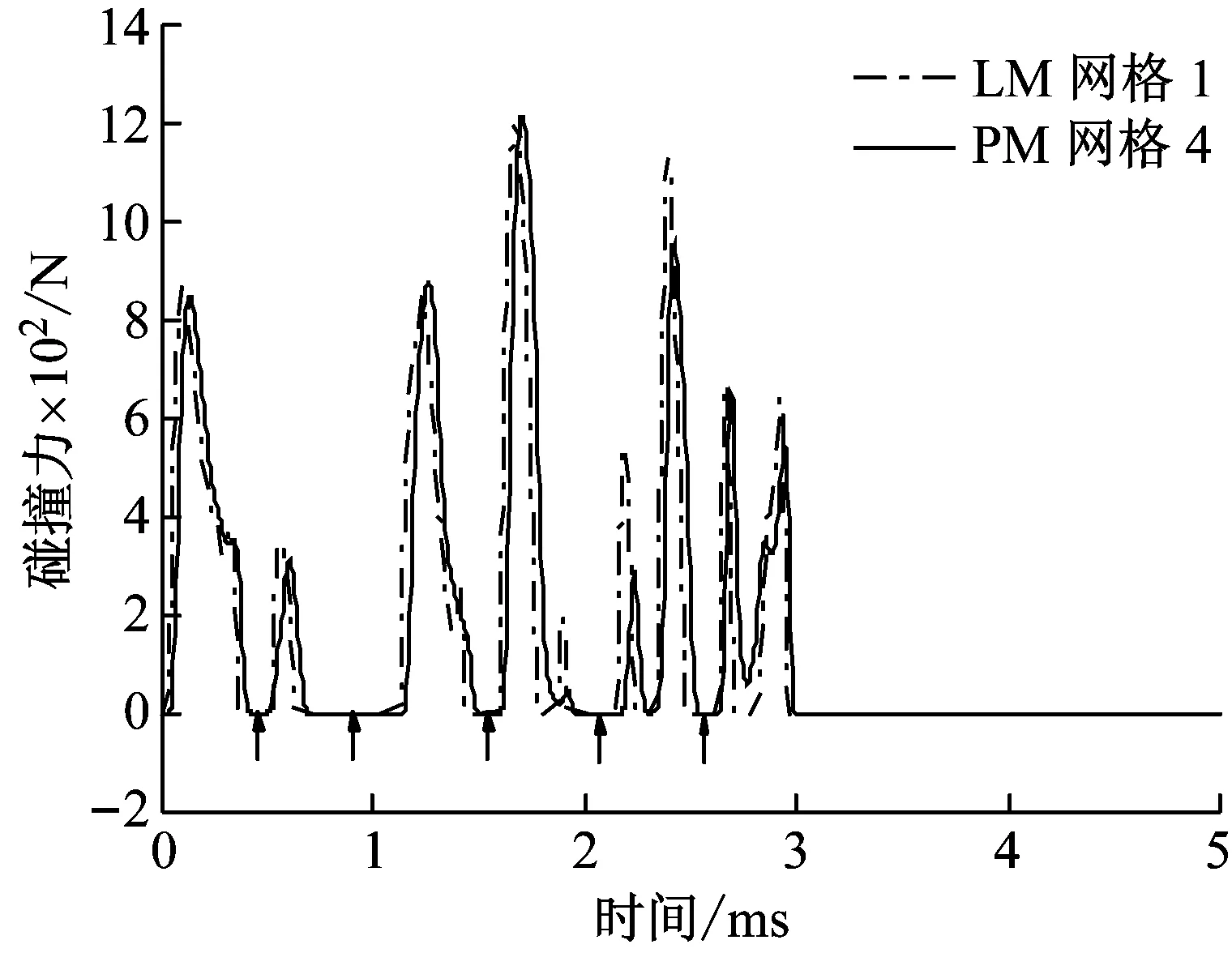
(d)图4 网格尺寸对仿真精度的影响Fig.4 Influence of mesh size on simulation accuracy

上述过程得到了碰撞力历程的数值收敛解，图4(d)显示出碰撞过程中碰撞力有多次过零。为了更直观地展示碰撞过程中接触点对的“接触-分离-再接触”现象，将杆上圆头的中心撞击点和梁上相应的被撞击点的位置关系作于图5中。可以看出由于弹性振动与碰撞的相互作用，使得杆和梁上的接触点对发生了多次分离。另外联系图4(d)看出，接触点对发生分离的时刻与碰撞力过零的时刻是一一对应的，说明该例中杆与梁的一次宏观碰撞的确产生了多次微碰撞过程。

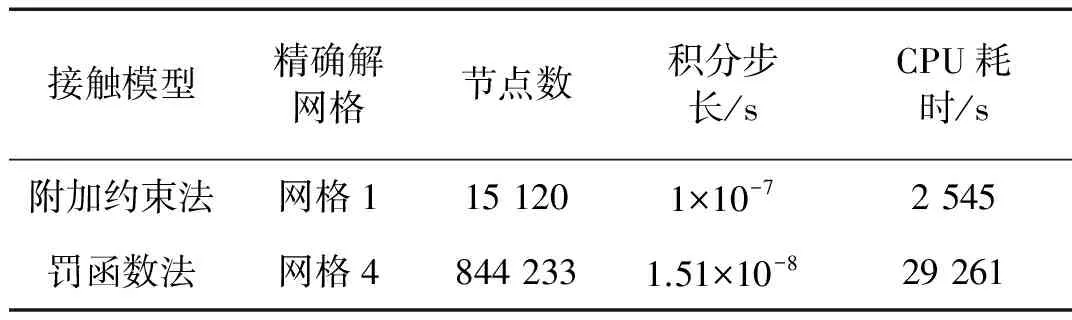
表3 罚函数法与附加约束法的计算规模比较Tab.3 Computation scale of the two contact methods

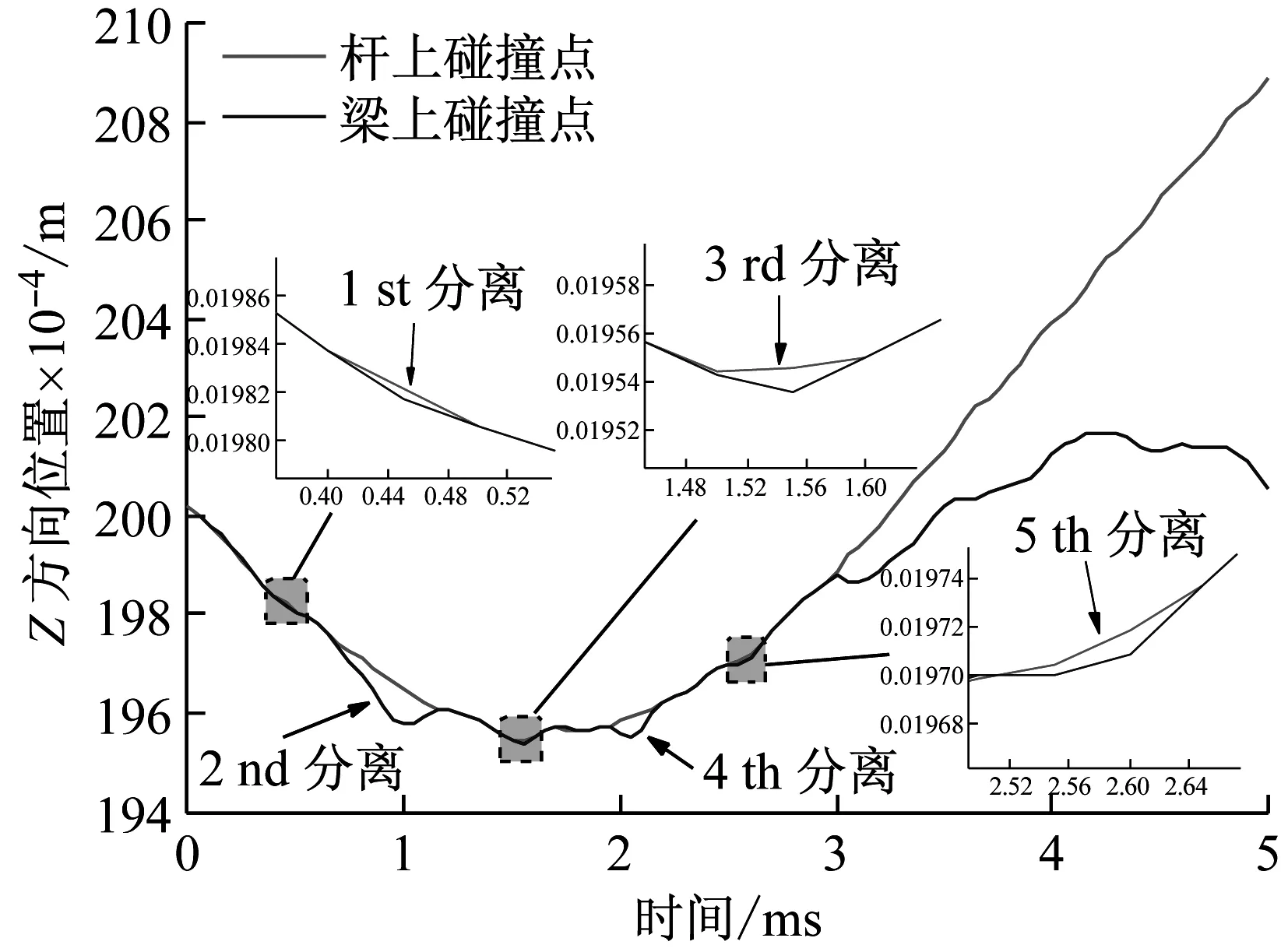
图5 碰撞过程中接触点对的位置Fig.5 The position of contact pair during the impact process

4 结 论

柔性体间的多次微碰撞行为会激发柔性体的高频振动，往往会对结构造成各种形式的损害。传统的方法多利用应力波理论求解简单结构的多次微碰撞问题，为了能正确预测任意形状柔性体间的多次微碰撞过程，本文基于有限元三维实体模型，分别用罚函数法和附加约束法对杆-梁碰撞问题进行仿真。对于罚函数方法，要对多次微碰撞过程中的碰撞力峰值、碰撞时间及碰撞次数进行准确预测，不仅需要选择合适的罚因子，还需要细密的网格单元支撑。对于附加约束方法，不需要人为选取刚度参数，并且即使在较粗糙的网格也能获得可靠的结果。因此在对多次微碰撞问题的动力学仿真中附加约束方法有一定优势。数值仿真得到的收敛结果表明，由于弹性振动与碰撞的相互作用，一次宏观碰撞中的确出现了多次“接触-分离-再接触”的微碰撞过程。

参 考 文 献

[1] KLISCH T. Contact mechanics in multibody systems[J]. Multibody System Dynamics, 1999, 2(4):179-188.

[3] FLORES P, KOSHY C, LANKARANI H, et al. Numerical and experimental investigation on multibody systems with revolute clearance joints[J]. Nonlinear Dynamics, 2011, 65(4):383-398.

[4] WYRICK D A, ADAMS D F. Residual strength of a carbon/epoxy composite material subjected to repeated impact[J]. Journal of Composite Materials, 1988, 22(8):749-765.

[5] STOIANOVICI D, HURMUZLU Y. A critical study of the applicability of rigid-body collision theory[J]. Journal of Applied Mechanics, 1996, 63(2):247-248.

[6] NARABAYASHI T, SHIBAIKE K, ISHIZAKA A, et al. Effects of key parameters on energy distribution and kinetic characteristics in collision of bar and beam[J]. Journal of Sound & Vibration, 2007, 308(3):548-562.

[7] 王琪, 庄方方, 郭易圆,等. 非光滑多体系统动力学数值算法的研究进展[J]. 力学进展, 2013, 43(1):101-111.

WANG Qi, ZHUANG Fangfang, GUO Yiyuan, et al. Advances in the research on numerical methods for non-smooth dynamics of multibody systems[J]. Advances in Mechanics, 2013, 43(1):101-111.

[8] WANG J, LIU C, ZHAO Z. Nonsmooth dynamics of a 3D rigid body on a vibrating plate[J]. Multibody System Dynamics, 2014, 32(2):217-239.

[9] 高玉华. 刚体撞块撞击弹性长杆的二次撞击分析[J]. 力学季刊, 1996(4):334-338.

GAO Yuhua. A prediction analysis of the second impact for an elastic bar impacting on a rigid block[J].Chinese Quarterly of Mechanics, 1996(4):334-338.

[10] 田阿利, 尹晓春. 自由飞行杆撞击过程中的二次撞击区[J]. 振动与冲击, 2008, 27(1):19-24.

TIAN Ali, YIN Xiaochun.Secondimpactzonefora free-flying rodtoimpactaclampedone[J].Journal of Vibration and Shock, 2008, 27(1):19-24.

[11] 段玥晨, 章定国. 基于弹塑性接触的柔性多体系统碰撞动力学[J]. 南京理工大学学报, 2012, 36(2):189-194.

DUAN Yuechen, ZHANG Dingguo.Flexible multibody system impact dynamics based on elastic-plastic contact[J]. Journal of Nanjing University of Science and Technology, 2012, 36(2):189-194.

[12] 刘锦阳, 洪嘉振. 闭环柔性多体系统的多点撞击问题[J]. 中国机械工程, 2000, 11(6):619-623.

LIU Jinyang, HONG Jiazhen.Impact with multiple contact points of flexible multibodysystem with closed loops[J]. China Mechanical Engineering, 2000, 11(6):619-623.

[13] SEIFRIED R, SCHIEHLEN W, EBERHARD P. The role of the coefficient of restitution on impact problems in multibody dynamics[J]. Proceedings of the Institution of Mechanical Engineers, Part K： Journal of Multi-body Dynamics, 2010, 1(K3):1-28.

[14] WEYLER R, OLIVER J, SAIN T, et al. On the contact domain method: a comparison of penalty and Lagrange multiplier implementations[J]. Computer Methods in Applied Mechanics & Engineering, 2012, 205(1):68-82.

[15] 王检耀, 洪嘉振, 刘铸永. 接触碰撞动力学的多变量选取方法[J]. 力学学报, 2014, 46(2):318-322.

WANG Jianyao, HONG Jiazhen, LIU Zhuyong.Multi-variable selection method in contact/impact dynamics[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(2):318-322.