离心泵隔舌区域压力脉动特性分析
程 伟,宋文武,万 伦,晏 祝,侯 洁
(西华大学能源与动力工程学院,四川成都610039)
压力脉动是由于泵内部空间的非对称结构使其内部流动出现复杂的非定常特性,使泵不但产生静态压力而且还会产生动态压力[1]。压力脉动的出现是一个不好的信号,设备的振动和噪声就是由于系统内压力脉动引起的,严重时会损坏设备[2]。
当前,针对离心泵内因流体诱发压力脉动的研究表明,离心泵内部流场的压力脉动、径向力与隔舌及隔舌与叶轮之间的间隙有关[3- 4]。窦唯等[5]分析了不同厚度隔舌对高速离心泵压力脉动的作用,推导出流体激振力的幅值与其隔舌厚度成正比。刘厚林等[5]对多级离心泵各级导叶流道内压力脉动规律进行了研究,发现压力波动幅值随泵级数增加而降低。袁寿其等[13]则对隔舌形状展开研究,对比了2个不同形状的隔舌对离心泵性能的影响。王洋等[6]分析了离心泵内部不稳定流动的原因,提出脉动源主要是隔舌所产生压力脉动。MAJIDI[7]通过模拟离心泵内部流场发现,叶轮和蜗壳的内流场呈现强烈的周期性。施卫东等[8]的研究表明,离心泵性能与隔舌安放角有关,调整隔舌安放角更利于得出更优的离心泵模型。
本文重点研究了离心泵在3种工况下的压力脉动特性,离心泵在0.8Q~1.2Q变流量工况下,叶轮内部流体的流动状况,分析了导致离心泵压力脉动特性,旨在为离心泵的优化设计和高效运行提供一定的建议与参考。
1 计算模型及数值求解方法
1.1 计算模型、网格划分
离心泵的模型参数为:流量Q=120 m3/h,扬程H=40 m,转速n=2 900 r/min,叶轮的叶片数为6片。计算区域包括进口段、叶轮、蜗壳和出口段4个部分。
本文利用商业软件ICEM对整个计算区域进行网格划分。为了使进入叶轮的流体更加合理,采用进口延长,同理蜗壳出口也进行延长处理。由于叶片扭曲度较高,所以采用加密非结构化网格,叶轮的网格单元数为2 270 000,蜗壳的网格单元数为1 020 000,整个水体模型总的网格单元数为4 440 000。网格无关性分析,取2 410 000与4 440 000网格进行对比分析,离心泵的扬程和效率稳定在1.5%以内。

图1 网格划分
为了监测离心泵内部压力脉动的情况,分别取监测点P1,P2,P3,P4和P5。计算模型的隔舌位置及监测点示意图如图2所示。

图2 监测点位置示意
1.2 湍流模型与非定常模拟设置
由于计算流体为不可压流体,所以采用雷诺平均动量方程来描述流动。考虑旋转与曲率影响,采用RNGk-ε湍流模型[9-10]。
非定常数值模拟时间步长设为0.011 49,经过120个时间步长,叶轮旋转一周。
2 压力脉动特性分析
2.1 不同工况下各监测点压力脉动时域图分析
为了方便下面的阐述,这里定义压力脉动系数Cp=(P-Pavg)/Pavg,其中P为静压,Pavg为静压平均值,Cp是指压力脉动振幅占静压平均值的比例。同时定义时间系数Cr=(t-tb)/(te-tb),该周期内压力脉动便用0~1的无量纲系数来表示,其中,tb为周期开始时刻的时间,te为周期结束时刻的时间。
图3所示为小流量(0.8Q)工况下,5个监测点压力脉动时域图。由图3可知:P1处脉动幅度最大,P2,P3,P4和P5处脉动幅度相应减弱。与图4相比,P1点为脉动最激烈处,其余各点相对较平稳。泵内湍流出现较强的不规则性,是由于离心泵处于小流量工况下引起的,表现为压水室各截面出现较突兀的峰值,尤其体现在P1,P2及P5测点处,说明离心泵在小流量工况运行时,压力脉动递增明显。

图3 小流量工况下监测点压力脉动时域
图4所示为设计工况(1.0Q)下,各个监测点压力脉动时域图。由图4可知:脉动周期性十分明显;P1处的压力脉动最为强烈,P2~P5的压力脉动相应减弱,而且在P3处最弱。压力脉动幅度差异的原因在于P1和P5点距离隔舌较近,受隔舌影响最大;P3点远离隔舌,使得该处压力脉动较小,同时两者对比结果没有差异,说明隔舌对该处的影响较小。除P3点外,其他4点的脉动幅值均不是对称分布,原因是旋转叶轮与蜗壳水流之间的动静干涉以及隔舌对流体的扰动作用,使得蜗壳内水流流动呈明显的不均匀性和三维紊流特征,且周期性波动十分规律,致使压水室内流体呈漩涡流形态。

图4 设计工况下监测点压力脉动时域
图5所示为大流量工况(1.2Q)下,单由图5可知,P1处压力脉动远大于其余各点脉动幅值,其余各监测点脉动幅值基本都处于较低水平,且各幅值偏离不大。舌蜗壳压水室的某截面上压力脉动幅值出现瞬间的峰值,这是由于大流量对隔舌的冲击振动更强烈。压水室各截面上的压力脉动幅值显然降低,其中P3处压力只有微弱降低。以上分析表明,在大流量工况下,隔舌能够抑制压水室各截面上的脉动情况,故可以减缓由于偏离设计流量而带来的压力脉动的锐增。
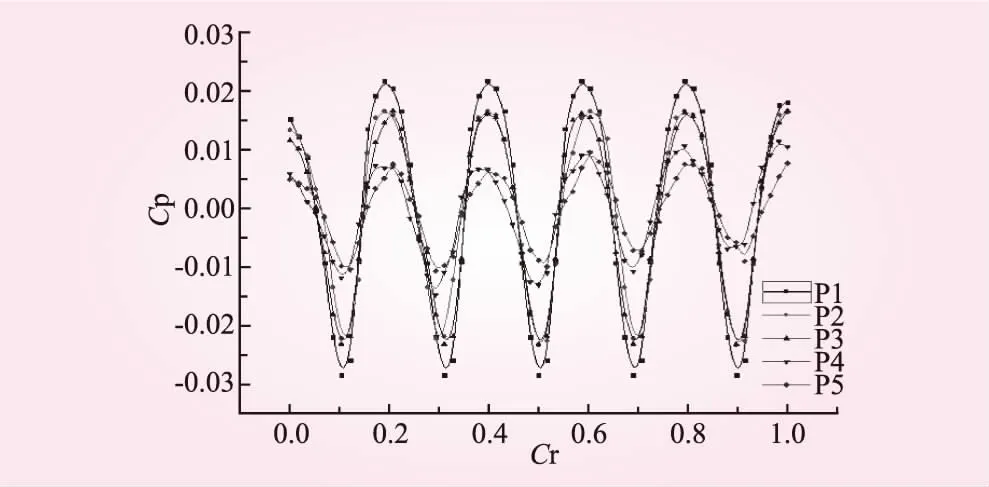
图5 大流量工况下监测点压力脉动时域
2.2 不同工况下各监测点压力脉动频域图分析
图6所示为对小流量工况下各个监测点进行快速傅里叶变换得到各监测点的压力脉动频域图。由图6可知:P1,P2和P3点主频处脉动幅度差异不大,P4点主频处略小,P5点处脉动比以上各点的都低。P1~P5点的压力脉动频率以1倍叶频为主,高频减少特别明显。其原因是流体进入压水室后,流体的速度能逐渐转化成压力能,静压的增加使压力脉动持续上升,但双隔舌的结构却能很好的对压力脉动削弱。以上分析表明,除因远离隔舌而压力脉动不明显的P3点外,在小流量工况下也能较好地改善压水室各截面的脉动情况。

图6 小流量工况下各个监测点压力脉动频域
图7所示为对设计工况下5个监测点进行快速傅里叶变换得到各监测点的压力脉动频域图。由图6可知:各监测点的压力脉动主频率都是1倍叶频附近,与叶轮通过频率基本一致;P1主频是各监测点处脉动幅度最高处,其余点次之,P5最低。在P4和P5处压力脉动主要集中在低中频附近。

图7 小流量工况下各个监测点压力脉动频域
图8所示为对大流量工况下5个监测点通过快速傅里叶变换得到各监测点的压力脉动频域图。由图8可知:P1点主频处脉动幅值最大,P3,P4,P5点在主频处的脉动幅值基本处于同一水平,P2处脉动幅值则处于相对较低值。5个监测点主频都是1倍叶频。P2点处时主频也是1倍叶频附近次主频为2倍叶频附近,高频部分显著增多;其原因在于:随着流体流量增加,在叶轮经过隔舌后,部分流体仍在叶轮内不停循环,并造成回旋,与蜗壳周期性撞击,即形成P2处高频率的压力脉动。依上所述,在大流量工况下,隔舌对附近区域影响较为明显。
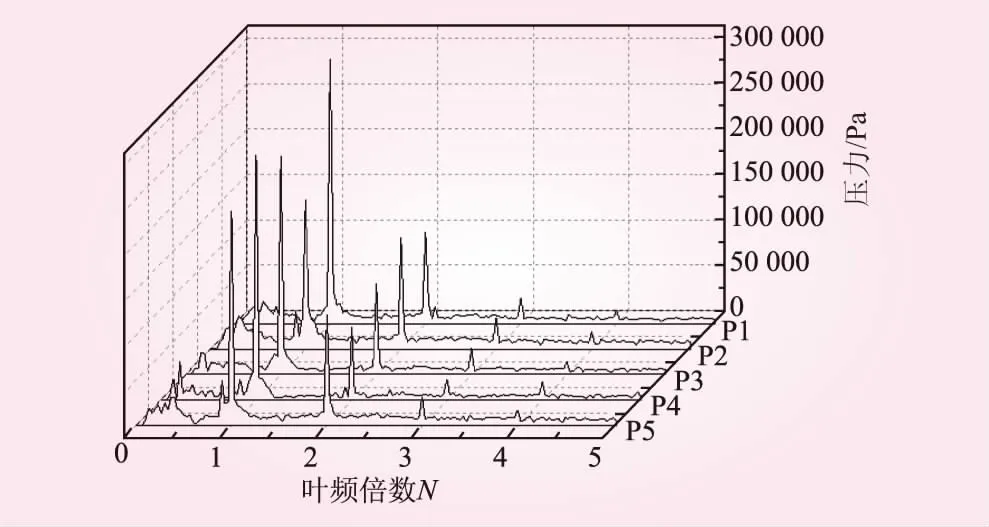
图8 小流量工况下各个监测点压力脉动频域
3 结 论
(1)受到隔舌影响流道内各观察点的压力脉动出现非常显著的周期性,而且在0.8Q、1.0Q、1.2Q工况下的5个监测点主频都是叶片通过频率。
(2)随着观察点与隔舌周向距离变大,脉动幅值逐渐减小,这时脉动主要是叶片通过频率,高频脉动成分较少。
(3)各个监测点的压力脉动频谱图通过快速傅里叶变换方法得到,可以初步得到实际测量仪器无法监测到的部位(如叶轮流道、蜗壳等)的压力脉动特性,对于了解隔舌影响内部流场压力脉动情况提供了有益的参考。
[1] 朱荣生, 苏保稳, 杨爱玲, 等. 离心泵压力脉动特性分析[J].农业机械学报, 2010, 41(11) : 43- 47.
[2] 袁建平, 付燕霞, 刘阳, 等. 基于大涡模拟的离心泵蜗壳内压力脉动特性分析[J]. 排灌机械工程学报, 2010, 28(4) : 311- 314.
[3] 胡全友, 刘小兵, 赵琴, 等. 蜗壳式混流泵压脉动特性研究[J]. 人民长江, 2016(10): 76- 80, 95.
[4] BARRIO R, PARRONDO J, BLANCO E. Numerical analysis of the unsteady flow in the near-tongue region in a volute-type centrifugal pump for different operating points[J]. Computers and Fluids, 2010, 39(5): 859- 870.
[5] 刘厚林, 周孝华, 王凯, 等. 多级离心泵径向导叶内压力的脉动特性[J]. 中南大学学报: 自然科学版, 2014, 45(9): 3295- 3300.
[6] 王洋, 代翠. 离心泵内部不稳定流场压力脉动特性分析[J]. 农业机械学报, 2010, 41(3): 91- 95.
[7] MAJIDI K. Numerical study of unsteady flow in a centrifugal pump[J]. Journal of Turbomachinery, 2005, 127(2): 363- 371.
[8] 施卫东, 徐焰栋, 李伟, 等. 蜗壳隔舌安放角对离心泵内部非定常流场的影响[J]. 机械农业学报, 2013, 44(1): 125- 130.
[9] 袁寿其, 衡亚光, 洪峰, 等. 2种隔舌模型对离心泵性能模拟的影响[J]. 排灌机械工程学报, 2013, 31(7): 553- 557.
[10] 魏立超, 宋文武, 石建伟, 等. 基于CFD的高速离心泵进口段流动数值模拟分析[J]. 热能动力工程, 2016(7): 103- 109, 138- 139.

