多站联动水位流量关系拟合方法研究

刘代勇，彭亚兰

(中国电建集团中南勘测设计研究院有限公司，湖南长沙410014)

0 引 言

水位流量关系是洪水成分分析、实时洪水预报研究中的重要内容，影响水位流量关系的因素很多，不仅包括河道冲淤、阻塞等几何因素，还有洪水涨落趋势、支流水量交换等水力因素。在平原河道水位流量关系的研究中，回水顶托、行蓄洪区调蓄等因素的影响显著。由于各种因素具有显著的不确定性，致使水文站点水位流量关系具有强烈的不稳定性与时变特征，水位流量关系十分复杂，难以精确估计。

近年来，研究人员对水位流量关系拟合技术做了大量探索。高兵役等[1]针对绳套曲线计算困难的特点，对校正因数法进行幂级数展开，提出了绳套型水位流量关系自动拟合的方法，并以衡山站实测洪水资料进行了验证，结果表明研究该法具有自动拟合方法速度快、精度高的特点。万凤鸣等[2]将综合落差指数引入水位流量关系研究中，采用多项式的形式、应用最小二乘法进行参数求解，对长江中游沙市、螺山、汉口3站的水位流量关系进行了模拟，结果表明落差指数的单值化方法能够将水位流量关系的拟合误差控制在较小的水平。王世安等[3]结合绳套曲线与单值化方法的特点，将绳套曲线分解为涨水段与落水段两部分，分别率定出两段水位流量关系曲线，研究表明该方法能够更好反映实际的水位流量关系。本文基于洪水波传播及相应水位法，提出多站联动水位流量关系拟合法，并以淮河小柳巷站点进行实例验证，确立一种更适于平原区水位流量关系模拟的方法。

1 多站联动的水位流量关系拟合法

常用的水位流量关系拟合方法主要有单值曲线法、绳套曲线法以及以上两类方法的改正法等。其中，单值曲线法通常将水位流量关系概化为单一曲线，其方程形式简单、易于推广；而绳套曲线则能更精确地反映受洪水涨落影响的复式水位流量关系，在洪水预报中具有一定的精度，应用更为广泛。

单值化方法往往通过建立试验站点水位、流量之间的二元函数关系实现，最常用的方法是将流量与水位分别视作二元一次方程的自变量与因变量，采用最小二乘法拟合历史观测数据，所得参数被认为可以用于反映当前站点的水位流量关系特征。即

Zt=a0Qt+c+ε

(1)

式中,Z为试验站水位；t为当前预报执行时刻；a0为单值化方程的系数；Q为试验站流量；c为常数项；ε为余项。

绳套曲线形式的水位流量关系常见于受洪水涨落影响明显的河段，绳套曲线定线困难，常用的方法有校正因素法、抵偿河长法等，一般需要通过反复试算。李致家等[4- 6]将绳套曲线分为涨水段与落水段，并采用最小二乘法对涨水、落水段水位流量点据单独定线，经2003年～2009年鲁台子站点5场洪水验证，取得了较好的模拟效果。

(2)

绳套曲线的特点在与峰顶和谷底的曲线曲率较大，而相应的实测资料较少；因此，在实际定线中依然有较多问题存在。

综上所述，无论是传统单值化方法还是绳套曲线方法，均只能对现有历史资料做事前定线，在实时洪水预报应用中两种方法的参数、方程结构固定，无法将最新的实测资料应用于水位流量关系的更新；同时，两种方法仅考虑同一站点、同一时刻水位与流量之间的转换关系，未考虑影响当前站点的其他因素。然而，在实时洪水预报应用中，这些因素均会影响洪水预报的精度。

河道相应水位预报方法是基于天然河道洪水波传播原理，分析洪水波在运动过程中，任意相位水位/流量自上而下传播时，沿程各站相应水位以及波速变化规律的方法。此类方法较好地考虑了洪水的平移与坦化作用，并在长江等流域洪水预报中验证了其可靠[7]。

基于此，本文借鉴相应水位方法，认为某测站水位、流量的变化与同相位上游站点的水文要素密切关联，提出多站联动的水位流量关系拟合方法MISC(Multi-station Interactive Stage-discharge rating Curve )，采用回归分析方法率定出该站点的水位流量关系。MISC法构建的回归方程如下：

ZN,t+l=a0Qt+l+(aNQN,t+bNZN,t)+…+
(a1Q1,t+b1Z1,t)+c+ε

(3)

式中，N为上游实测站点数目；a为流量系数；b为水位系数；l为预见期且不大于洪水波从上游传递到下游的滞时(汇流滞时)；c为常数项；ε为余项。该方法主要是将某测站实时水位流量关系表示为历史时刻多站水位流量的函数，逐步回归分析获取主要影响因素，率定出水位流量关系中的各项参数，进而建立时变的水位流量关系。

2 实例应用

2.1 试验流域简介

小柳巷水文站设立于1981年4月，位于安徽省明光市小柳巷镇，是淮河干流入洪泽湖最后的控制站，流域面积123 950 km2，下游100 m为泊岗引河工程，下游630 km为洪泽湖。受附加比降影响，该站水位流量关系呈复杂的逆时针绳套曲线，由于每次洪水的涨落率不同，相应的绳套曲线大小也不同，各场洪水绳套曲线的参数存在很大差异，水位流量关系较难确定。此外，下游回水顶托、干流洪水调度等因素，对该站水位流量关系影响较大。

2.2 水位流量关系拟合效果对比

在实时洪水预报的应用中，应用MISC法构建水位流量关系时，需要考虑试验站点的洪水预报预见期。《淮河流域使用水文预报补充方案》对1982年～2005年的历史洪水进行分析，统计显示试验流域河道洪水滞时大致在0～27 h。图1显示，洪峰传播时间集中分布在0～20 h之间，在构建水位流量关系时，只需考虑24 h或更短时间之内上游水位、流量对小柳巷站水位流量关系的影响。

图1 1982年～2005年吴家渡-小柳巷洪峰传播时间分布

设定水位流量关系应用于预见期为3、6、12、24 h的实时洪水预报场合。

选用20050707号洪水用于模拟试验，洪水起止时间为2005/07/07 14:00～2005/07/28 14:00，模拟试验采用小柳巷水位为因变量，将预报时刻小柳巷流量或上游站点水位、流量视作自变量，分别采用三种拟合方法构建小柳巷站水位流量关系，模拟结果如图2所示。为方便描述，文中约定水位低于14 m为低水，14～16 m为中水，16 m以上为高水。

图2显示，MISC法的模拟结果大致分布在45°线附近，表明预见期为3、6、12、24 h的洪水预报应用中，MISC法的模拟水位值与实测值较接近，表现出较高的模拟精度与稳定性能；传统单值化的方法在低水状态下模拟效果较好，但中水、高水部分的水位值与实测值有明显差距；绳套曲线方法总体模拟效果比单值化方法效果有很大提高，尤其在中水、高水部位模拟效果较好。

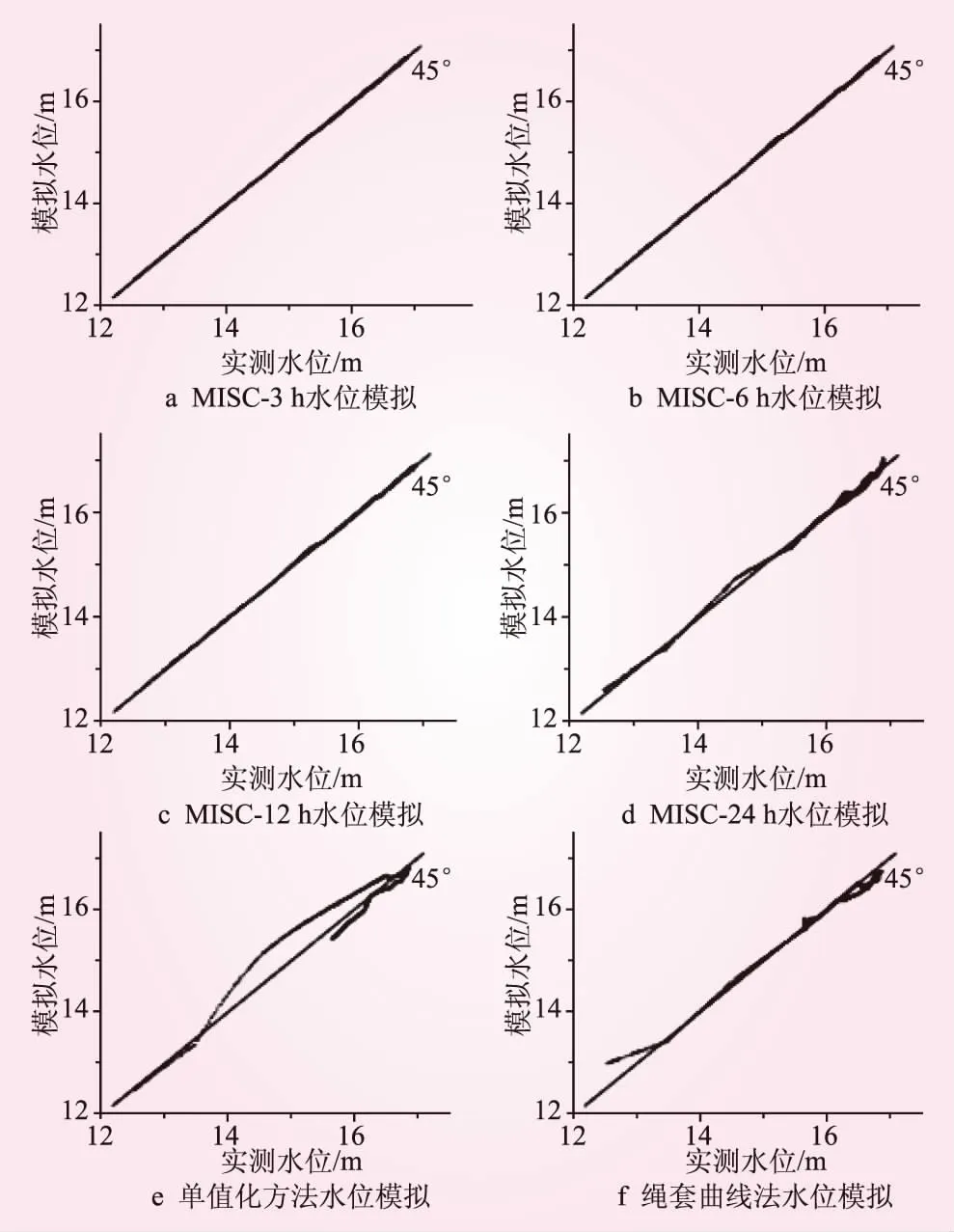
图2 MISC、单值化以及绳套曲线法模拟小柳巷水位流量关系效果对比

图2模拟结果还显示，随着预见期的增长，MISC方法的模拟水位值越来越偏离45°线。即，MISC方法的模拟精度逐渐降低。因此，精度与预见期在水位流量关系拟合方面依然存在着不可调和的矛盾。

为精确对比3种方法在模拟试验的3～24 h洪水预报中的效果，本文以确定性系数为指标，统计三种方法在低水、中水、高水部位的模拟精度。确定性系数又称纳什效率系数(Nash Efficiency Coefficient， NSE)，是由Nash与Sutcliffe在1970年提出的统计指标，广泛用于描述计算值与目标值拟合精度。NSE的取值范围为(-∞，1]，其值越大，表明计算值与目标值越接近，模拟效果越好。3种方法在低水、中水、高水部位模拟效果的NSE指标统计值见表1(预见期3～24 h)。

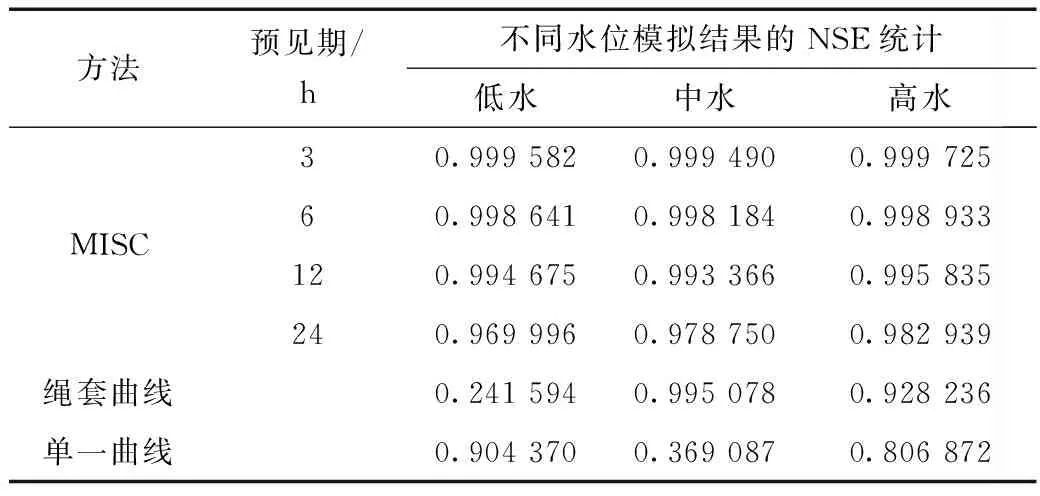
表1 MISC、单值化与绳套曲线方法在低水、中水、高水部位模拟结果的NSE统计

统计结果显示，MISC法模拟高水部位的NSE指标值较大，中水部位的NSE值次之，低水部位的NSE值相对最小；且MISC法模拟高水部位的NSE值随预见期的变更而变化的幅度最小，中水部位次之，低水部位随预见期的变化的变幅最大。研究结果表明，MISC法在高水部位的模拟精度与稳定性最高，适用于高水位的实时洪水预报。

2.3 模拟结果分析

偏相关系数是衡量多个变量中某两个变量之间线性相关程度的指标。与简单的相关系数相比，它能够避免变量之间可能存在的共变联系的影响，能更为合理地判断两变量之间是否存在直接的线性相关关系。偏相关系数取值范围[-1，1]，其绝对值越接近1，表明两变量之间线性相关程度越高。

本文为了分析MISC法模拟效果好于其他两种方法的原因，统计了MISC法中各变量的偏相关系数，各方案中自变量与因变量(小柳巷水位)的偏相关系数见表2。表中的Zobs(Qobs)表示实时洪水预报中站点的最近时刻的水位(流量)实测值(或预报执行时刻的实测水位(流量值))，Q表示预报截止时刻站点的流量计算值。

三种方法共有变量(小柳巷Q)统计结果显示，该共有变量在三种方法的偏相关系数大致在0.995以上，偏相关系数均较大，表明小柳巷Q与Z显著。小柳巷Q在绳套曲线方法涨水、落水段的相关系数有明显差别，表明在落水段两者的线性相关关系相对较弱，在落水段可能存在更多的其他因素同时影响着小柳巷水位的变化。考虑到小柳巷站点下游有泊岗引河工程，因此模拟结果是合理的。

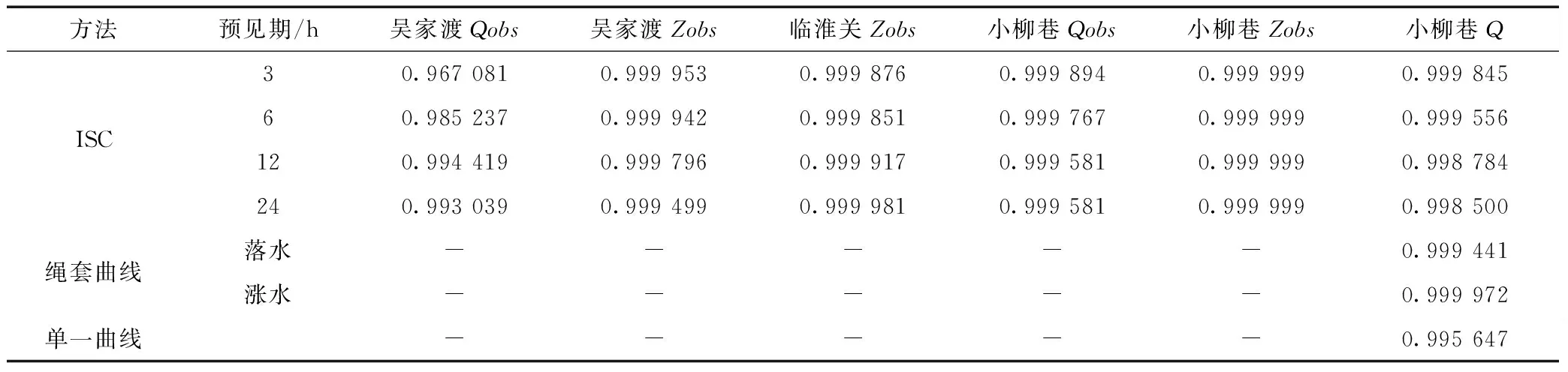
表2 MISC、单值化与绳套曲线方法中自变量与因变量偏相关系数

注：表中“-”表示该方法中无此变量。

MISC法在不同预见期洪水预报应用中的的统计结果显示，小柳巷站预报执行时刻水位值与预报截止时刻的水位值之间的偏相关系数达到0.999 999，远高于小柳巷在预报截止时刻的流量值以及实测期内其他变量的偏相关系数值。研究结果表明，除预报时刻小柳巷Q之外，实测期内的水文变量也对预报时段内小柳巷水位有强烈影响，不能忽略实测期内水文变量对预见期内小柳巷水位的影响。因此，传统的水位流量关系拟合方法(如：单值化、绳套曲线方法)仅考虑小柳巷流量对水位的影响，而建立二元方程描述其水位流量关系的做法，是较为低效、不精确的。

根据MISC法中各变量在不同预见期偏相关系数的变化，考虑到上游站点的水位比流量相关系数更大(见图3)，应进一步分析MISC法的应用性能。

图3 MISC法中各变量随预见期变化过程

由图3可见，“吴家渡Zobs” 偏相关系数随预见期的提高成减小趋势；而“吴家渡Qobs”则是先升后降。这种现象进一步印证了前面所提到的水位与流量变化并不同步，不成明显线性相关关系的结果。下面重点对吴家渡Qobs进行分析。

吴家渡Qobs的偏相关系数先升后降，在预见期为12 h时达到最大值点0.994 419。考虑到模拟试验采样数目有限，仅选用预见期为3、6、12和24 h 4种情况，未能详细考虑3～6 h、6～12 h之间的偏相关系数变化，则变量临淮关Zobs的偏相关系数的实际最小值点应该在横坐标为6～24 h的范围内。根据各站实测记录显示，吴家渡水位与流量的最大值均出现在第218个时刻，小柳巷洪峰水位出现在第234时刻。在本场洪水中，吴家渡至小柳巷的洪峰滞时大致为16 h。在16 h之前的吴家渡来水尚未传播到小柳巷站，因此其偏相关系数相对较小；而在16 h之后的吴家渡来水已经通过小柳巷继续向下传播，此时吴家渡Qobs的偏相关系数虽然相对较高，但是比16 h预见期对应时刻的偏相关系数值已经明显减小。模拟结果与考虑洪水传播因素的实际情况较为一致，说明MISC法较为准确的贴合河道水流运动的物理机理，是一种比较可靠的水位流量关系拟合方法。

综上所述，多站联动水位流量关系拟合方法(MISC)能够将更多与测站水位、流量相关的因素引入到水位流量关系拟合体系中，能够准确反映水位流量关系的实时变化。利用MISC法，可以在洪水演进模型中计算出流量，继而由实时更新的水位流量关系转换得到水位模拟值，经验证可以有效防止误差扩大，可作为水动力学模型稳定、可靠的下边界条件。本研究成果已经集成到《淮河小柳巷以上实时洪水预报与调度系统》中，在2003年～2014年的多场实时洪水预报应用中被验证可靠，为洪水预报技术水平的提高发挥了积极作用。

3 结 论

本文基于洪水波传播及相应水位法，提出多站联动水位流量关系拟合法(MISC)，其在淮河小柳巷站点进行的应用研究表明，MISC法能在不同预见期的实时洪水预报应用中取得比传统单值化、绳套曲线方法更为精确而稳定的模拟结果，能够有效地将与当前站点相关站点的水文变量用于水位流量关系的更新，对当前水位流量关系拟合研究与分析有十分重要的意义，对实时洪水预报技术水平与预报精度的提高有积极的作用。

[1] 高兵役, 李正最. 洪水期水位流量关系绳套曲线的直接拟合[J]. 水文, 1998(5)： 27- 30．

[2] 万凤鸣, 龙立华, 张悦. 单值化处理长江中游主要断面水位流量关系研究[J]. 长江科学院院报, 2012(12)： 5- 9, 33．

[3] 王世安, 佟少先, 秦敏, 等. 水位流量绳套曲线过程分析及建立模型[J]. 黑龙江水利科技, 2002(2)： 8- 9．

[4] 李致家, 李纪人, 韩从尚. 河道流量和水位模拟的综合法介绍[J]. 人民黄河, 1990(2)： 16- 20．

[5] 常露, 刘开磊, 姚成, 等. 复杂河道洪水预报系统研究——以淮河王家坝至小柳巷区间流域为例[J]. 湖泊科学, 2013(3)： 422- 427．

[6] 刘开磊, 李致家, 姚成, 等. 水文学与水力学方法在淮河中游的应用研究[J]. 水力发电学报, 2013(6)： 5- 10．

[7] 包为民. 洪水预报信息利用问题研究与讨论[J]. 水文, 2006(2)： 18- 21．