基于深度学习的支持向量机的信息安全检测和预警研究

王贵喜

(92493部队 一分队， 葫芦岛 125001)

0 引言

随着互联网技术和网络规模的不断增加，网络入侵检测成为互联网安全研究的重要内容和热点问题。所谓入侵检测是指通过网络数据的监测，检测出网络安全的入侵行为和入侵类型，并在此基础上发出警报和进行预警处理。传统的网络入侵检测存在检测正确率低、扩展性差和容易发生误报的缺点，基于历史数据的机器学习方法可以通过历史数据建立网络入侵检测模型，并对未来所监测出的网络未知入侵攻击进行高效识别，具有很强的扩展性和适应性。目前很多学者将机器学习方法引入网络入侵检测研究，方法主要集中在神经网络[1]、贝叶斯算法[2]、支持向量机[3]、极限学习机[4]等，这些方法的特征选择过度依赖人工，存在表达能力有限以及模型训练受制于类别标签，对于复杂网络环境下的网络入侵数据检测的稳定性、可靠性和正确性均难以得到保证。

本文将深度学习[5-6]与支持向量机结合，提出一种基于深度信念网络和支持向量机的网络信息安全检测算法。在复杂环境下，DBN-SVM可以自动提取网络入侵特征属性数据，通过不同算法在所用训练集的比例为20%、30%和40%的准确率和误报率对比可知，相同训练集比例情况下，DBN-SVM较DBN和SVM模型具有更高检测准确率和更低误报率。

1 深度置信网络

Hinton等[5]人于2006年提出深度置信网络(Deep Belief Nets，DBN)算法，掀起了深度学习研究的热潮，DBN模型是一种深层混合模型，它由多个受限玻尔兹曼机以串联的方式堆叠而形成的一种深层网络。本文采用无监督方式的贪心算法对原始数据进行预训练，进而采用有监督方式的SVM算法对整个网络的参数进行微调，最终获得重构误差最小的输出数据。如图1所示。

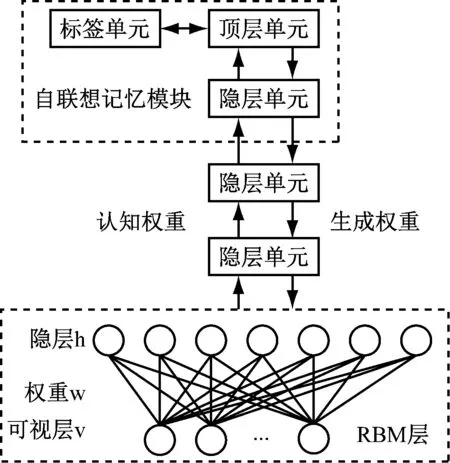
图1 DBN模型

1.1 受限玻尔兹曼机

受限玻尔兹曼机[6](Restricted Boltzmann Machines，RBM)是一类具有对称连接，层间全连接，层内无连接的无向随机神经网络，其网络结构分为两层，一层为可视层v，表示观测数据；另一层为隐层h，表示特征提取器；w为两层之间的连接权重。如图2所示。

图2 RBM模型

设所有可见单元和隐单元均为二值变量，如式(1)。

∀i,j,Vi∈{0,1},hj∈{0,1}

(1)

其中：vi表示第i可视单元的状态，hi表示第j隐单元的状态。则对于一组给定状态(v,h)，RBM作为一个系统所具备的能量定义为式(2)。

(2)

其中：wij表示可视单元i与隐单元j之间的连接权重，ai和bi分别是可视单元和隐单元的偏置量。假定RBM参数为θ，θ={wij,ai,bj}。当参数确定时，可以得到(v,h)的联合概率分布，为式(3)、式(4)。

(3)

(4)

对于真正的问题，由RBM所定义的v分布是非常重要的，即联合概率的边缘分布P(v|θ)，为式(5)。

(5)

另设中间变量F(v)为式(6)。

(6)

对(5)式求导后取负后，则为式(7)。

(7)

在上述推导中，如要使RBM系统稳定，系统的能量需要最小化。即使公式(2)达到最小值，则需要令F(v)最小，或者令P(v|h)最大。

由RBM的结构具有对称性，当给定隐单元状态时，各可视单元的激活状态条件独立，即的激活概率为式(8)。

(8)

由于RBM层内无连接、层间全连接可知，当给定v时，各隐单元之间的状态也条件独立，即hj的激活概率为式(9)。

(9)

其中：σ(z)=1/(1+exp(-z))为激活函数。基于上述算法，RBM采用迭代法进行训练，最终得到学习参数θ=(wij,ai,bi)的值，以适应给定的观测数据。可以通过最大化训练集(T)上的RBM的最大对数似然函数来获得参数[7]为式(10)

(10)

由式(10)我们发现梯度很难计算，因此，RBM采用吉布斯抽样来取得其近似值。一般来说，只需要使用吉布斯抽样来获得足够好的近似值。所以可以得到更新规则的参数为式(11)～式(13)。

-W←W+ε(p(h1|v1)v1-p(h2|v2)v2)

(11)

-a←b+ε(v1-v2)

(12)

-b←b+ε(h1-h2)

(13)

其中ε表示学习率(Learning Rate)。

1.2 DBN-SVM网络

在正向传播过程中，输入层神经元负责从外部接收输入信息并将其传递给隐含层中的神经元，将隐含层的信息传递到输出层，在误差的反向传播过程中，由于实际输出与预期输出之间存在误差，当输出误差超过期望误差时，则会进行误差的反向修正。在本文中，利用深度网络预训练过程优化RBM参数，同时对整个DBN网络结构进行SVM算法微调，如图3所示。

图3 DBN-SVM结构模型

2 支持向量机

(14)

其中，ω、C、ξi分别表示权重向量、误差惩罚函数和松弛变量；φ(x)和b分别表示核空间映射函数和偏差。Lagrange函数L构造如[8]式(15)。

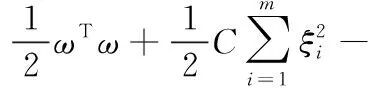
(15)

其中，ai表示Lagrange乘子。根据KKT条件，对公式(15)求偏导可得[9]，为式(16)。

(16)

消去ω和ξi，可得公式(17)，如式(17)。

(17)

其中，Q=(1，…,1)T，A=(a1,a2,…,am)T，Y=(y1,y2,…,ym)T，通过式(17)的求解，可得到SVM数学模型的估计[10-11]式(18)。

(18)

其中，K(x,xi)=exp(-||x-xi||2/2σ2)。

3 DBN_SVM训练算法

本文深度置信网络训练时通过自低到高逐层训练RBM将模型参数初始化为较优值，再使用BP算法对网络进行微调，使得模型收敛到接近最优值的局部最优点。由于RBM可以通过对比散度(contrastive divergence，CD)等算法快速训练，这样就可以避免了直接训练DBN的高计算量，将模型化简为对多个RBM的训练问题，解决了模型训练速度慢的问题，能够产生较优的初始参数，经过这种方式训练后，有效地提升了模型的建模以及推广能力。具体的训练学习过程如下：

1) 输入网络入侵特征属性数据X，并用CD算法充分训练第一层RBM；

2) 通过第一层训练RBM获得的权重和偏移量作为第二层的输入量训练RBM；

3) 重复1)和2)过程直到训练完所有的RBM；

4) 最后一层RBM的输出作为第一层的输入，实现模型参数的初始化；

5) 确定模型参数后，在DBN自联想记忆模块利用有监督的SVM算法自上而下的调整整个模型的参数。

算法流程如下：

Input：网络入侵特征属性数据X(训练集和测试集)、网络入侵类别。

Output：网络入侵类别。

Initialize：W1：输入层→隐含层的权值，B1：输入层→隐含层的阈值

W2：隐含层→输出层的权值，B2：隐含层→输出层的阈值

η：步长

1 for 1:2 000//循环次数

2 输入层→隐含层：

3z1=E·W1+B1，Z1=S(z1) //激活函数S

4 隐含层→输出层：

5z2=E·W2+B2，Z2=S(z2)

7 反向传播

8 输出层→隐含层的梯度

9δ2=J′

10 隐含层→输入层：

11δ1=J′·Z2

12 更新权值参数

15 取步骤b)中RBM的隐含层L2的输出值矩阵Z1代表编译后的数据，其中Z1是一个特征数为隐含层L2神经元个数m的矩阵为Z=Z1,Z2,…,Zm，并且取步骤b)中训练好的权值W2和阈值B2。

16 确定模型参数后，在DBN自联想记忆模块利用有监督的SVM算法自上而下的调整整个模型的参数。

4 实验仿真

4.1 数据来源

为了说明DBN_SVM算法进行网络入侵检测的效果，选择KDD CUP99数据集为实验对象[12-14]，该数据集包含41个特征，其中涉及字符和数值型，网络入侵的标签类型分别是正常、U2R、Probe、DOS和R2L，其编码类型，如表1所示。

表1 KDD CUP99数据集标签编码

4.2 数据预处理

为了使得网络入侵数据属性特征位于同一数量级内，运用公式(19)对属性数据进行归一化处理，如式(19)。

(19)

4.3 DBN_SVM参数设置

DBN_SVM模型的参数如表2所示。

表2 DBN_SVM参数表

输入特征数据维数为41，输出类别为5类，因此输入层和输出层的神经元个数分别为41和5，隐含层神经元结构为100-70-30-61。

4.4 评价指标

为了说明不同方法的网络入侵检测方法的好坏，选择准确率(Accuracy Rate，AR)和误报率(False Alarm Rate，FR)作为评价指标，其式如[15-16]式(20)、式(21)。

(20)

(21)

式中，A表示总样本数量；B表示正确分类的样本数量；C表示被误报为入侵的正常样本数量；D表示正常样本总数。

4.5 实验结果与分析

4.5.1 不同训练集比例

针对KDD CUP99数据集，DBN、SVM和DBN_SVM分别运用20%-40%的总样本数量进行训练，剩余的样本进行测试，测试结果，如图4所示。

图4 DBN_SVM检测精度图

由图4DBN_SVM检测精度图可知，当所用训练集的比例为40%时，DBN_SVM的检测准确率高达97.8%，当所用训练集的比例为30%和20%时，DBN_SVM的检测准确率分别为97.1%和95.1%，通过对比可知，随着当所用训练集的比例的增加，准确率的提升效率降低，从而说明DBN具有强大的抽象表示能力，在只有很少的数据量的情况下，就能训练出表达能力很强的模型，同时体现出SVM良好的预测能力。

4.5.2 不同算法对比

为了说明DBN、SVM和DBN_SVM分别在所用训练集的比例为20%、30%和40%的准确率和误报率，DBN、SVM和DBN_SVM的检测准确率和误报率分别如表3、表4和图5和图6所示。

表3 不同算法检测准确率

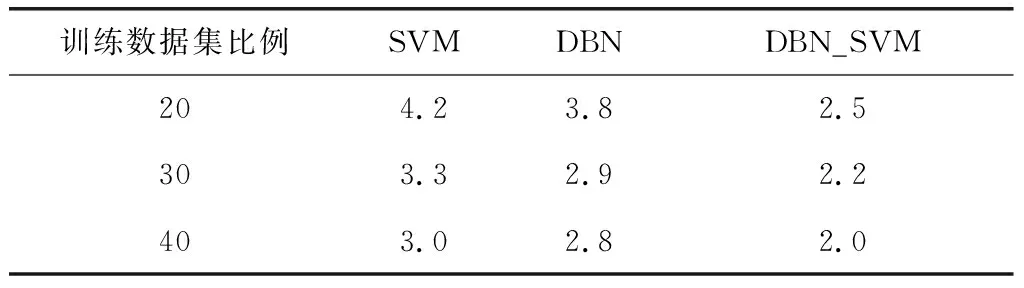
表4 不同算法检测误报率

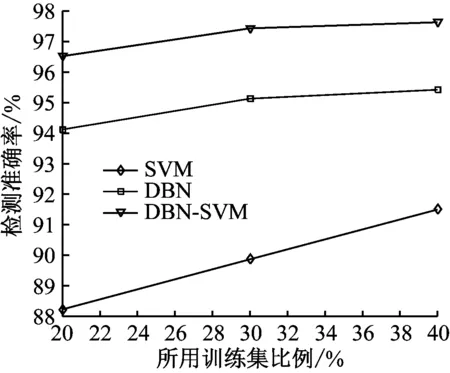
图5 准确率对比图

图6 误报率对比图

通过不同算法在所用训练集的比例为20%、30%和40%的准确率和误报率对比可知，相同训练集比例情况下，DBN_SVM较DBN和SVM模型具有更高检测准确率和更低误报率；随着训练集比例的增加，DBN、SVM和DBN_SVM的检测准确率和误报率分别呈现增加和降低的趋势，从而说明DBN_SVM进行网络信息安全检测具有更高检测准确率和更低的误报率，效果优于DBN和SVM模型。

5 总结

传统的网络入侵检测存在检测正确率低、扩展性差和容易发生误报的缺点，结合DBN模型的自学习能力、建模能力和较强的鲁棒性的优势，将DBN与支持向量机结合，提出一种基于深度信念网络和支持向量机的网络信息安全检测算法。研究结果表明，与DBN和SVM相比，DBN_SVM进行网络入侵检测具有更高的检测准确率和更低的误报率，为网络入侵检测和预警提供新的方法和途径。

[1] 刘羿. 蝙蝠算法优化神经网络的网络入侵检测[J]. 计算机仿真, 2015, 32(2):311-314.

[2] 王春东, 陈英辉, 常青,等. 基于特征相似度的贝叶斯网络入侵检测方法[J]. 计算机工程, 2011, 37(21):102-104.

[3] 谢伟增. 人工蜂群算法优化支持向量机的网络入侵检测[J]. 微型电脑应用, 2017, 33(1):71-73.

[4] 李新磊. 改进布谷鸟算法优化极限学习机的网络入侵检测[J]. 激光杂志, 2015(1):105-108.

[5] Lecun Y, Bengio Y ,Hinton G. Deep learning[J]. Nature,2015,521(7553)：436-444.

[6] Hinton G E, Osindero S, Y W. A Fast Learning Algorithm for Deep Belief Nets[J]. Neural Computation, 1960, 18(7):1527-1554.

[7] 李春林, 黄月江, 王宏,等. 一种基于深度学习的网络入侵检测方法[J]. 信息安全与通信保密, 2014(10):68-71.

[8] 李佳. 混合杂草算法优化支持向量机的网络入侵检测[J]. 计算机应用与软件, 2015(2):311-314.

[9] 王雪松, 梁昔明. 改进蚁群算法优化支持向量机的网络入侵检测[J]. 计算技术与自动化, 2015(2):95-99.

[10] 陶琳, 郭春璐. 改进粒子群算法和支持向量机的网络入侵检测[J]. 计算机系统应用, 2016, 25(6):269-273.

[11] 张小琴，贾郭军.一种采用粗糙集和遗传算法的支持向量机[J]. 山西师范大学学报(自然科学版)，2013(1)：35-38.

[12] 马磊娟, 王林生. 改进最小二乘支持向量机的网络入侵检测[J]. 微型电脑应用, 2017, 33(7):76-79.

[13] 梁辰, 李成海, 周来恩. PCA-BP神经网络入侵检测方法[J]. 空军工程大学学报·自然科学版, 2016, 17(6):93-98.

[14] 华辉有, 陈启买, 刘海,等. 一种融合Kmeans和KNN的网络入侵检测算法[J]. 计算机科学, 2016, 43(3):158-162.

[15] 夏栋梁, 刘玉坤, 鲁书喜. 基于蚁群算法和改进SSO的混合网络入侵检测方法[J]. 重庆邮电大学学报(自然科学版), 2016, 28(3):406-413.

[16] 袁开银, 费岚. 混合粒子群优化算法选择特征的网络入侵检测[J]. 吉林大学学报:理学版, 2016, 54(2):309-314.

[17] 马勇. 模糊推理结合Michigan型遗传算法的网络入侵检测方案[J]. 电子设计工程, 2016, 24(11):108-111.

[18] 石云, 陈钟, 孙兵. 基于均值聚类分析和多层核心集凝聚算法相融合的网络入侵检测[J]. 计算机应用研究, 2016, 32(2):518-520.