创造性思维训练在课堂教学中的探索与应用

山东滨州市沾化区下洼镇第一小学（256803）

创造性思维是指人类开拓创造意识和创新精神的思维活动，具体表现为不墨守成规，创造性地提出问题和解决问题。开发人的创造力，培养新一代人的创新素养，是社会文明发展的主题，笔者在二十多年的小学数学教学生涯中，对创造性思维能力的训练做了一些有意义的探索与应用，在此将一些经验分享给广大教师。

一、发散思维的训练

发散思维是一种不按常规方法解题，而从多方面寻求答案的思维方式，这是创造性思维的核心，它具有灵活性、变通性、独创性等特征。在平时的课堂教学中，教师可以安排以下训练，让学习层次不同的学生的思维得到发散，促进其创造性思维能力的形成与发展。

1.给题目补充问题。

【题目】某车间有男工人50名，女工人40名，__？

教师可将本题安排在“分数应用题”教学后让学生练习，让他们进一步明确“分数应用题”的结构特点，掌握题目的数量关系。对于该题目，一般学生都能补充以下问题：

（1）男工人人数是女工人人数的几分之几？

（2）女工人人数是男工人人数的几分之几？

（3）男工人比女工人多几分之几？

（4）女工人比男工人少几分之几？

思维能力比较好的学生还会补充：

（5）男工人人数占全车间人数的几分之几？

（6）女工人人数占全车间人数的几分之几？

（7）全车间人数是男工人人数的几分之几？（几倍）

（8）全车间人数是女工人人数的几分之几？（几倍）

思维能力更好的学生还可以补充：

（9）男工人人数比全车间人数少几分之几？

（10）女工人人数比全车间人数少几分之几？

（11）全车间人数比男工人人数多几分之几？

（12）全车间人数比女工人人数多几分之几？

……

2.用简便方法计算。

【题目】25×48

学生在教师的引导下，得出如下结果：

（1）25×40+25×8；

（2）20×48+5×48；

（3）25×4×12；

（4）25×40+25×4×2；

（5）25×40+25×4+25×4。

教师可将本题安排在学生学习了“乘法分配律”之后，这样既便于学生选择最简捷的算法进行计算，又利于激发学生的探索兴趣。

在数学课堂上，教师要最大限度地给学生提供发散思维的机会，使学生得以充分发挥自己的聪明才智。

3.一题多解。

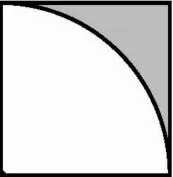
图1

【题目】如图1，已知正方形的面积是40平方厘米，求图中阴影部分的面积。

这是一道难度较大的题目，教师可将其安排在“圆的面积”教学后让学生练习，以便培养学生思维的变通性和独创性。思维能力一般的学生总是试图求出正方形的边长后，再求阴影部分的面积，而思维能力较好的学生则会采用以下方法解决问题。

解法一：先把正方形面积扩大10倍，即400平方厘米，那么正方形的边长（即四分之一圆的半径）就是20厘米，阴影部分的面积为400－3.14×202÷4=86（平方厘米），然后缩小10倍就得到实际阴影部分的面积为86÷10=8.6（平方厘米）。

解法二：先把正方形面积缩小10倍，即4平方厘米，那么正方形的边长就是2厘米，则阴影部分的面积就是 4-3.14×22÷4=0.86（平方厘米），然后扩大 10 倍就得到实际阴影部分的面积为0.86×10=8.6（平方厘米）。

解法三：因为正方形面积是40平方厘米，所以边长×边长=40（平方厘米）。本题中，正方形的边长正好是四分之一个圆的半径，由此得出，半径×半径=40（平方厘米）或r2=40（平方厘米），四分之一圆的面积就是3.14×40÷4=31.4（平方厘米），从而得出阴影部分面积为40－31.4=8.6（平方厘米）。

二、直觉思维的训练

直觉思维具有直接、跳跃、迅速、敏捷等特点，人们常根据直觉和假想对问题的答案做出判断，从而使问题迅速得到解决。在教学中，教师可以通过以下训练，促进学生直觉思维能力的发展。

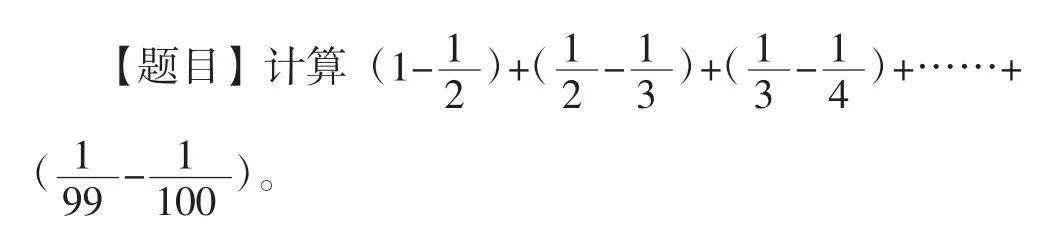
教师可将本题安排在“异分母分数加减运算”教学后让学生练习。直觉思维能力较好的学生发现，相邻两个括号内有一加一减的两个相同的数，展开括号后直接加减便可得到直觉思维能力更好的学生通过对整个算式结构的观察，能够一眼看出答案，从而跳过复杂的运算过程，由原式直接得出

三、联想思维的训练

联想思维就是从当前的某一事物想到与之相关的另一事物，或根据它们之间的某些相似之处和关系，去推测两者之间在其他方面可能具有的相似之处和关系。联想思维是沟通新旧知识之间的桥梁，也是创造性思维的重要组成部分。在教学中，教师可以利用以下素材训练学生的联想思维。

【题目】用简便方法计算：

本题可结合“带分数退位减法”教学，让学生将该题作为一种思考性的题目进行练习，这样既可突破“带分数退位减法”的教学难点，又可进一步提高学生简便计算的能力。对于该题，思维能力较好的学生能联想到整数减法运算中“差的变化性质”和“减法的运算性质”，他们会采用以下方法计算：

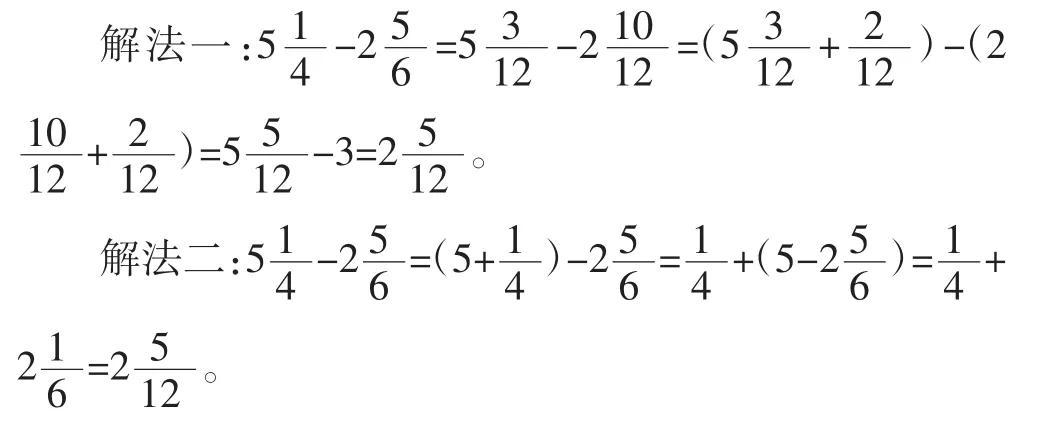
【题目】填空：梯形的一底逐渐缩小为一点时，梯形变成（ ）形；梯形的一底逐渐增大到与另一底相等时，梯形变成（ ）形。

本题可安排在三角形、平行四边形、梯形等概念教学之后让学生练习，让学生从运动的角度去理解几种平面图形之间的内在联系。

总之，学生创造性思维的训练和培养，应贯穿于整个教学活动中，只要教师认真研究和探索创造性思维的训练方法，并将其融于教学中，就能更好地培养学生的创新意识，使越来越多具有创造性思维的学生脱颖而出。