基于一阶及二阶DIC方法的 常应变剪切带的测量误差分析

杜亚志， 王学滨,2， 董 伟， 冯威武， 侯文腾

(1. 辽宁工程技术大学 力学与工程学院， 辽宁 阜新 123000； 2. 辽宁工程技术大学 计算力学研究所， 辽宁 阜新 123000)

1 引 言

目前，CT技术、立体成像技术、数字图像相关(digital image correlation, DIC)方法[1～5]等先进的观测手段均被用于测量剪切带内外微结构特征、研究剪切带的发展演化等。

文献[6]针对DIC方法中图像的亚像素插值误差较大的问题，提出了一种基于B样条插值核的插值滤波器;文献[7]通过对散斑图进行平移，比较了梯度法、曲面拟合法及N-R(Newton-Raphson)法的精度;文献[8]提出了一种散斑图质量评价参数——平均灰度梯度;根据文献[8]提出的参数，文献[9]提出了一种散斑图质量评价参数——平均一阶及二阶灰度梯度商;文献[4]使用整像素精度的DIC方法测量了水平常应变剪切带的宽度;文献[5]根据梯度塑性理论制作了含应变梯度的水平剪切带，比较了一阶及二阶DIC方法的位移场、应变场及应变梯度场的测量结果的差异。

为了解基于DIC法的剪切带的测量精度，本文制作了简单剪切条件下水平(倾角为0°)和倾斜(倾角为60°)常应变剪切带，并使用DIC法对剪切带内、外的位移场、应变场和宽度进行了测量；分析了形函数、子区尺寸及测点间距对测量结果的影响。

2 剪切带的制作方法

常见的剪切带模型为简单剪切模型，在该模型中，剪切带内的变形是简单剪切，剪切带外仅有刚体位移。在水平常应变剪切带中，剪切位移为水平位移，若以剪切带中心线上任意点为原点建立直角坐标系x′O′y′,x′和y′分别为剪切带的切向和法向，则有剪切带水平位移计算公式：

s(y′)=γ0y′

(1)

式中：γ0为上述水平剪切带的剪应变；y′为剪切带的法向坐标，y′∈[-w/2,w/2]，w为剪切带宽度。

在该模型中，剪切带的倾角θ为零，而在通常情况下剪切带是倾斜的。文献[2]中仅简单提及了倾斜剪切带的制作方法，即“首先，将一张实验图片旋转60°；然后，在一定位置进行常应变简单剪切；最后，再将图像反向旋转60°，得到包含倾斜剪切带(倾角为60°)的图像”。这里采用简单剪切模型及文献[2]提出的制作方法制作。具体步骤如下：

(1)定义剪切带边界。理论上，剪切位移是剪切带法向坐标的连续函数，而在剪切带制作过程中，仅对图像中离散的像素进行操作。图1给出了垂直于剪切带的一列像素、剪切带边界的位置及该列像素位移的示意图。在图1中,像素用小正方形表示，像素的中心点用圆点表示，剪切带边界用两条平行线段表示;图1(a)为剪切带边界在两个相邻像素之间；图1(b)为剪切带边界在像素的中心。于是产生了在位移曲线中剪切带宽度的定义不同，宽度分别为w1和w2。在图1(b)中，剪切带内靠近边界的点的位移等于最大剪切位移，据此制作剪切带，有利于与有关的理论结果作对比。

(2)对剪切带外上下两盘进行刚体平移，平移量为γ0w2。

(3)使用仿射变换方法对图像进行变形，使用光滑性较好的双三次样条函数对图像进行插值。

图1 剪切带的两种边界的定义

图2给出了源图像及含剪切带的图像。图2(a)为一幅散斑图[10]，据此制作了水平剪切带(图2(b))和倾斜剪切带(图2(c))，其中，γ0=-0.1745，w=30像素，θ=60°。

图2 源图像及含剪切带的图像

3 结果分析

在图像坐标系xOy下，从图2(a)变形至图2(b)，根据式(1)可计算出最大水平位移为2.62像素，垂直位移、水平线应变εx及垂直线应变εy的理论值均为零，剪应变的理论值γxy=γ0=-0.174 5。 使用基于粒子群优化算法及N-R迭代的粗-细DIC方法[3]分别对从图2(a)变形至图2(b)、从图2(a)变形至图2(c)的位移和应变进行了计算，计算区域如图2(a)所示(水平剪切带，使用计算区域1；倾斜剪切带，使用计算区域2)。

3.1 水平剪切带的结果分析

3.1.1 一阶DIC方法的结果分析

图3给出了基于一阶DIC方法的从图2(a)变形至图2(b)的结果，其中两条虚线代表剪切带的边界。子区尺寸为31像素×31像素(简称为31像素)，测点数量为23×19，测点间距为5像素。

图3 一阶DIC方法的水平剪切带的位移场、应变场及相关系数

从图3(a)和3(b)中可以发现:图像上、下两部分的位移矢量场有较大差别,上部分位移向左，下部分位移向右，且两部分位移的大小基本相等，这与带外区域平动相符；在上、下两部分之间，存在一个明显的位移梯度带，带内的水平位移在法向变化较大，这与剪切带的位置(图3(b)中的两条平行线段之间的区域)对应。该位移梯度带的宽度稍大于剪切带宽度，这表明，在剪切带边界附近，位移场存在一定的误差。

从图3(c)中可以发现:在远离剪切带及剪切带中心线附近的区域，垂直位移均在零附近，这与理论值接近；在剪切带边界附近，垂直位移在-0.15和0.2像素之间随机变化，表明在剪切带边界垂直位移的误差限较大。

从图3(d)和3(e)中可以发现:在远离剪切带及剪切带中心线附近的区域，两种线应变在零附近；

在剪切带边界附近，两种线应变在-0.02～0.02之间随机变化。从图3(f)中发现:在剪切带内，γxy在-0.16～-0.08之间，大于理论值-0.174 5；在剪切带边界附近，γxy在-0.08～0之间，表明γxy存在一定的误差。

从图3(g)中可以发现:在远离剪切带及剪切带中心线附近的区域，相关系数均大于0.999，表明位移误差限较小；在剪切带边界附近，相关系数在0.993～0.999之间，表明位移误差限较大。

3.1.2 形函数对位移和应变的影响

为了减小随机误差的影响，对图3中相同y坐标的19个点的位移和应变求均值。图4为不同DIC方法的位移和应变。

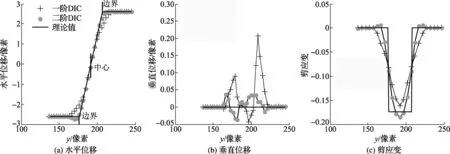
图4 不同DIC方法的位移及应变

从图4(a)中可以发现:当测点远离剪切带(y>225像素或y<160像素)时，两种DIC方法的水平位移均等于理论值；在剪切带内及附近(y=160～225像素)，两种DIC方法的水平位移均有一定的误差;在剪切带中心，位移误差均基本为零；从剪切带中心到剪切带边界，位移误差限逐渐增大，且一阶DIC方法比二阶DIC方法的水平位移误差限大;从剪切带边界到远离剪切带的测点，一阶DIC方法的水平位移误差限逐渐减小，趋于零，最大误差限约为0.6像素,而二阶DIC方法的水平位移最大误差限约为0.3像素。整体上，在剪切带内及附近，二阶DIC方法比一阶DIC方法的位移误差限小。从图4(a)、4(b)中可以发现:与水平位移误差限相比，垂直位移误差限较小;图4(b)中一阶DIC方法及二阶DIC方法的垂直位移的范围分别为-0.05～0.21像素和-0.05～0.05像素,这也表明，在剪切带内及附近，二阶DIC方法比一阶DIC方法的位移误差限小。

由图4(c)可以发现:在剪切带内，两种DIC方法的剪应变均是变化的，在剪切带中心剪应变最小,一阶DIC方法的剪应变均大于理论值，而二阶DIC方法的剪应变小于理论值;在剪切带边界，两种DIC方法的剪应变基本相等，约为理论值的一半;从剪切带边界至带外约20像素范围内，一阶DIC方法的剪应变逐渐增加，均小于零(理论值),而二阶DIC方法的剪应变较为复杂。

3.1.3 子区尺寸对位移和应变的影响

图5给出了从图2(a)变形至图2(b)的剪切带的位移和应变的分布规律，子区尺寸分别为21、41和61像素，其余计算参数同图3。与图4类似，已对相同y坐标的19个点的位移和应变求平均。

从图5(a)、5(b)中可以发现:随着子区尺寸的增加，剪切带内及附近区域(y=150～230像素)的绝大部分测点的位移误差限逐渐增加;当子区尺寸不同时，位移及位移误差均中心对称，对称中心为剪切带中心(y=192像素)。下面以剪切带中心上部(y<192像素)为例进行分析。剪切带中心附近测点的位移误差基本为零;当测点逐渐远离剪切带中心时，位移误差先增加，后减小，最后趋于零。在剪切带边界(y=177像素)，位移误差达到峰值；在位移误差峰值附近(y=147～192像素)，位移误差基本对称分布。对这种现象进行解释如下：

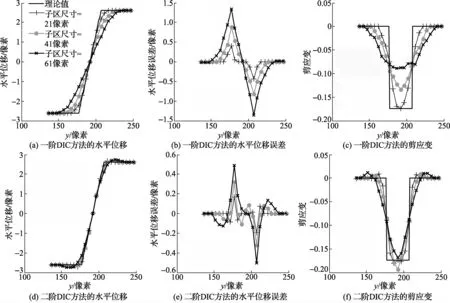
图5 子区尺寸对位移和剪应变的影响

对于子区中心点在剪切带边界附近的情况，无论其位于剪切带内或带外，一阶DIC方法中的变形均匀性假设不适用，因此位移误差限较大。当子区中心点在剪切带外时，子区覆盖的一部分剪切带区域是干扰区域;同样，当子区中心点在剪切带内时，子区覆盖的一部分剪切带外区域是干扰区域。当上述子区的中心点与剪切带边界的距离相等时，子区中干扰区域尺寸占子区尺寸的比例相等，此时，位移误差相等(图5(b))。当子区中心点在剪切带边界处时，该比例达到最大值0.5，此时位移误差达到最大值或最小值。因此可以推测，位移误差与干扰区域的尺寸占子区尺寸的比例有关。对于剪切带中心附近的子区，当其仅包含带内区域时，满足变形均匀性假设，因此位移误差限较小；随着子区尺寸的增加，当子区超出剪切带时，子区覆盖的两块剪切带外区域是干扰区域。剪切带中心附近测点的位移误差限较小，这可能与干扰区域对计算结果的影响较小有关。

从图5(d)、5(e)可以发现:对于二阶DIC方法的结果，随着子区尺寸的增加，剪切带内及附近(y=147～237像素)测点的位移误差限基本上逐渐增大。从图5(b)、5(e)可以发现:当子区尺寸相同时，对于剪切带内及其附近测点的位移，二阶DIC方法的位移误差限通常比一阶DIC方法的小，这是由于二阶DIC方法中，子区的变形可以是不均匀的。

从图5(c)、(f)可以发现:在剪切带中心，随着子区尺寸的增加，一阶及二阶DIC方法的剪应变的误差基本上逐渐增加；在子区尺寸相同时，二阶DIC方法的剪应变误差比一阶DIC方法的小。

3.1.4 测点间距对应变的影响

图6给出了测点间距分别为2、5及10像素时一阶及二阶DIC方法的剪应变。随着测点间距的增加，在远离剪切带的区域(y=135～150像素、235～250像素)，剪应变接近理论值；在剪切带内，剪应变-坐标曲线由陡峭变得平缓。在剪切带内及附近，随着测点间距的增加，一阶DIC方法和二阶DIC方法的剪应变有所不同：一阶DIC方法的剪应变逐渐偏离理论值；在剪切带边界外各5像素，二阶DIC方法的剪应变的误差随着测点间距的增加而减小；在剪切带中心附近(y=187～197像素)，二阶DIC方法的剪应变的误差由负值变为正值。

当测点间距分别为2、5及10像素时，一阶DIC方法的剪切带宽度分别为70、75及90像素，为理论值的2.3～3倍；二阶DIC方法的剪切带宽度均为70像素，为理论值的2.3倍。两种DIC方法的剪切带宽度均大于理论值，这可解释如下：在采用中心差分方法时，一点的应变是根据周围多个测点的位移得到的，剪切带外测点的应变可能被高估，由此导致剪切带宽度被高估。

图6 测点间距对剪应变的影响

3.2 倾斜剪切带的结果分析

图7给出了二阶DIC方法的从图2(a)变形至图2(c)(包含倾斜剪切带)的位移矢量场、水平位移、垂直位移、εx、εy、γxy及相关系数的等值线图，其中，两条虚线代表剪切带的两个边界。样本子区尺寸=31像素×31像素，测点数量为63×19，测点间距为5像素。可以发现：(1)在远离剪切带的位置，测点的位移比较均匀，应变基本为零，相关系数较大(大于0.999 8)，表明这部分测量结果比较准确；(2)在剪切带内及附近，应变比较集中，应变局部化带的宽度的计算值均大于剪切带宽度的理论值,相关系数的范围为0.998 6～0.999 8，略小于远离剪切带处的值。

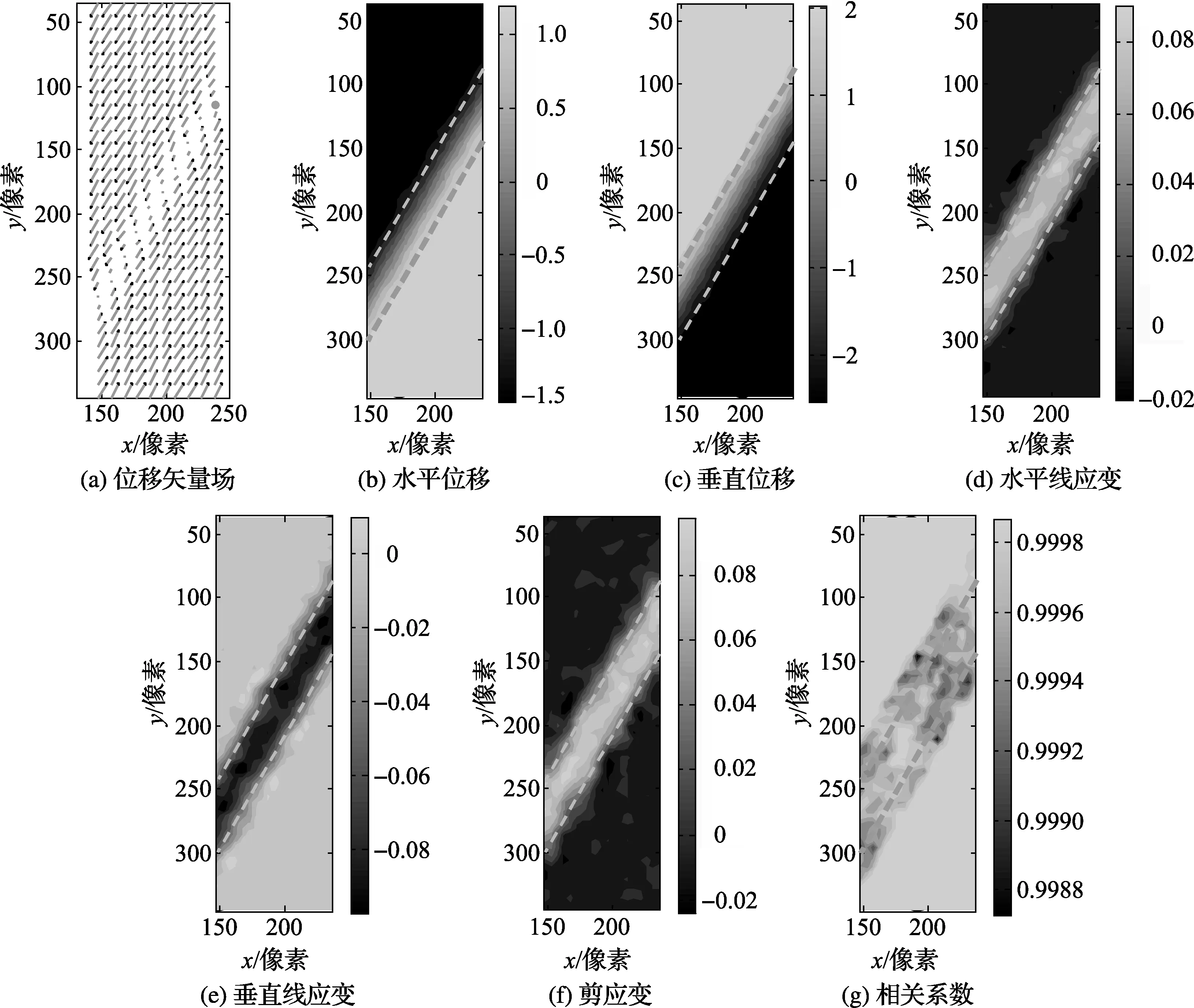
图7 二阶DIC方法的倾斜剪切带的位移场及应变场

由图3和图7可以发现，针对水平和倾斜剪切带的各种计算结果类似，不再赘述。

4 结 论

为了了解基于DIC法的剪切带的测量精度，本文制作了水平和倾斜的常应变剪切带，并使用DIC法对剪切带内、外的位移场和应变场进行了计算，得到以下结论：

(1)在剪切带边界附近，一阶或二阶DIC方法的位移误差限较大，这是因为这些区域的变形不均匀，子区覆盖一部分剪切带。子区尺寸越大，或测点距离剪切带边界越近，位移误差限越大。一般地，对剪切带边界附近测点进行计算时，二阶DIC方法的位移误差限比一阶DIC方法的小，这应与在二阶DIC方法中允许子区的变形是不均匀的有关。

(2)随着测点间距的增加，一阶或二阶DIC方法的剪切带法向的剪应变-坐标曲线由陡峭变得平缓，剪切带宽度逐渐增加。

[参考文献]

[1] Bhandari A R, Inoue J. Experimental study of strain rates effects on strain localization characteristics of soft rocks[J].SoilsandFoundations, 2005, 45(1): 125-140.

[2] Rechenmacher A L, Abedi S, Chupin O,etal. Characterization of mesoscale instabilities in localized granular shear using digital image correlation[J].ActaGeotechnica, 2011, 6(4): 205-217.

[3] 王学滨, 杜亚志, 潘一山. 基于DIC粗-细搜索方法的单轴压缩砂样的应变分布及应变梯度的实验研究[J]. 岩土工程学报, 2012, 34(11): 2050-2057.

[4] 王学滨, 杜亚志, 金石. 基于数字图像相关方法的剪切带宽度的影响因素分析[J].世界科技研究与发展, 2012, 34(3): 359-363.

[5] 王学滨, 杜亚志, 潘一山. 考虑一阶和二阶位移梯度的数字图像相关方法在剪切带测量中的比较[J]. 工程力学, 2013, 30(7): 282-287.

[6] 任茂栋, 梁晋, 唐正宗, 等. 数字图像相关法中的优化插值滤波器[J]. 西安交通大学学报, 2014, 48(7): 65-70.

[7] 资新运, 耿帅, 赵姝帆, 等. 3 种亚像素位移测量算法的比较研究[J]. 计量学报, 2015, 36(3): 260-267.

[8] 潘兵, 吴大方, 夏勇. 数字图像相关方法中散斑图的质量评价研究[J]. 实验力学, 2010, 25(2): 120-129.

[9] 杜亚志, 王学滨, 冯威武, 等. 基于一阶及二阶灰度梯度的散斑图质量评价方法[J]. 光学技术, 2017,43(2):169-175.

[10] Zhou P, Goodson K E. Subpixel displacement and deformation gradient measurement using digital image/speckle correlation[J].OpticalEngineering, 2001, 40(8): 1613-1620.

[11] Lu H, Cary P D. Deformation measurements by digital image correlation: Implementation of a second-order displacement gradient[J].ExperimentalMechanics, 2000, 40(4): 393-400.