钢桁拱桥极值点失稳问题有限元分析
刘 洋,王 楠
(1.武汉港湾工程质量检测有限公司,武汉 430040;2.海工结构新材料及维护加固技术湖北省重点实验室,武汉 430040;3.中交武汉港湾工程设计研究院有限公司,武汉 430040)
现代钢拱桥建设在我国起步较晚,理论研究也落后于国外[1,2],得益于近几十年来国内大跨度拱桥的大量修建,其跨径不断增加,矢跨比提高,相对刚度减弱,可见高耸的桁架结构受侧向风荷载作用不容忽略[3,4],尤其在主拱悬拼过程中,侧向刚度较小,对侧向风荷载更为敏感,因此不得不关注钢桁架拱桥的抗风稳定性。目前国内对钢桁架拱桥稳定性的研究重点主要集中在恒载、施工临时荷载和汽车活载等作用下的第一类稳定性[5],对风荷载的分析仍然以影响因素的形式加以考量,较少关注施工过程中的抗风稳定性,尤其是极值点失稳问题,为此,对钢桁架拱桥施工过程中的弹塑性稳定分析很有必要。
1 极值点失稳问题的有限元分析
极值点失稳问题的分析过程可以理解为同时考虑几何非线性和材料非线性的极限承载力问题,结构达到极限承载能力时,表现为结构完全崩溃,有限元[1,6]中,即为考虑几何非线性和材料非线性对结构刚度的影响,通过求解非线性平衡方程,得出结构的极限承载力,求解方法通常采用荷载增量法[6-8]。结构在外荷载不断增加的过程中,结构刚度也不断呈非线性变化,当材料进入塑性状态后,材料非线性对结构刚度也会产生影响,随着结构刚度矩阵趋于奇异,结构承载能力达到极限,在整个过程中,可用增量方程表示为[6]
(0[K]o+0[K]L+0[K]σ){Δu}i={ΔP}i
(1)
其中,{ΔP}i为第i步荷载增量,{Δu}i为荷载增量{ΔP}i导致的节点位移增量。在求解极限承载力时,有如下两个问题需要注意。
1.1 荷载增量的选取
在程序计算过程中,荷载是被分成若干步荷载的形式施加到结构上的,在计算开始时,位移近似呈线性变化,随着荷载的不断加大,初应力刚度影响越来越显著,切线刚度矩阵和单元刚度矩阵行列式的值逐渐减小,荷载位移曲线趋于平稳,因此在荷载增量选取时可以在计算开始时适当取得大点,节约计算时间,同时,在将要达到极限承载能力时,较大的荷载增量使得计算结果难以收敛,因此需要逐步减小荷载增量,在程序分析时,可以采用自动荷载步的方式。ANSYS有限元软件实现自动荷载步的方式主要是打开自动步长,根据前一荷载步荷载在分析计算时的迭代次数来确定当前荷载步的荷载增量,若前一步荷载在设定的迭代次数内未能收敛,则采用二分的形式重新划分荷载增量并继续计算。另外选取荷载增量的方式还可以依据特征刚度法[9],表示为
[Ki]={ΔP}i/Δui
(2)
其中[Ki]表示第i步结构的特征刚度,{ΔP}i为第i步荷载增量,Δui为第i步结构位移中最显著的一个节点增量位移分量,第i+1步荷载增量的计算依据第i步结构的特征刚度而选取,表示为
{ΔP}i+1/{ΔP}i=[Ki+1]/[Ki]
(3)
由此可以确保荷载增量开始较大,随着结构趋于失稳时,荷载增量逐渐减小,由于[Ki+1]是未知的,则下一荷载步的荷载增量可以改写为
{ΔP}i+1={ΔP}i·[Ki]/[Ki-1]
(4)
1.2 位移增量法
荷载增量法仅适用于极值点前的屈曲分析,在极值点处,结构的切线刚度矩阵的行列式值为零,因此无论荷载增量多小,结构都不可能发生相应的位移增量以达到平衡,也就是说计算不能收敛,为此荷载增量法无法逾越极值点,为进行后屈曲分析,我们可以在极值点处,采用位移增量法以替代荷载增量法。一般而言,可以将刚度矩阵重新排列,使得要控制的位移列到最后一项,对原刚度矩阵进行分块,增量平衡方程可表示为
(5)
式中,Δλ为控制荷载增量步长的系数,(R1,R2)T为求解迭代过程中的不平衡力向量。上式可进一步改写为
(6)
在极值点处迭代时,通过给定位移增量Δu2的值,可以求出相应的位移增量Δu1和荷载增量步长的系数Δλ,由于位移增量影响结构的刚度矩阵,求解过程中需要反复迭代运算,当(R1,R2)T的值在收敛容差内,则计算收敛。
2 工程背景
2.1 项目简介
此项目北起于规划永安南路,自北向南布置,经规划潘台路、航空路、规划路、唐白河、滨河路,后止于规划金沙路,主线全长1.945 km。主线桥起讫点桩号为K0+200~K2+145,其中桥梁起讫点桩号为K0+340.5~K1+913.5,全长1.573 km,主桥为跨径组合(70+240+70) m的下承式钢桁架拱桥,桥面全宽43.9 m。
全桥桥型布置图如图1所示。
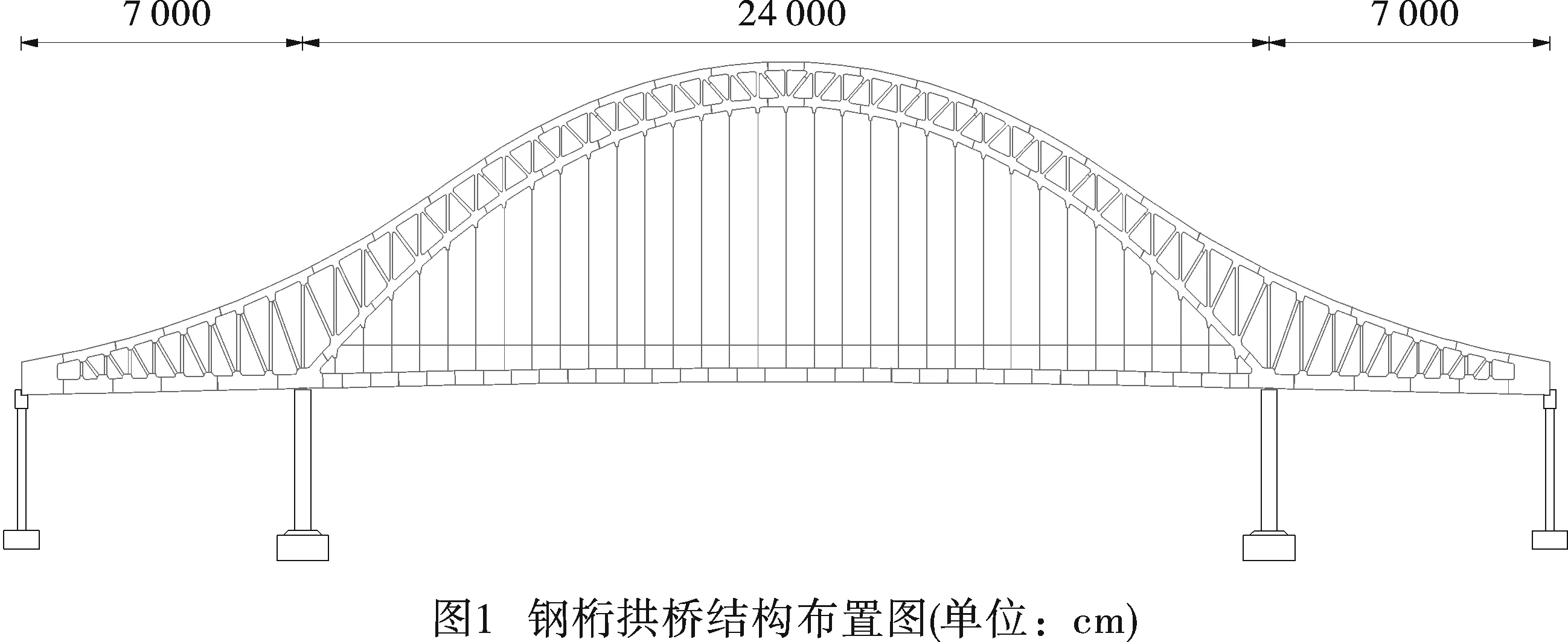
2.2 建立计算模型
该文采用ANSYS有限元软件进行分析计算,计算模型中钢桁杆件、横纵梁和临时吊索塔架构件均采用BEAM189单元进行模拟,吊杆、扣索、背索和临时系杆均采用LINK10单元模拟,桥面板采用SHELL63单元模拟,实常数根据实际桥面板厚度设置,吊索塔架与主体结构进行铰接,通过不耦合相应两节点绕横桥向的转动自由度加以实现。主体结构及临时施工构件的几何参数按照设计图纸取值,钢材的弹模取为206 GPa,拉索的弹模取为195 GPa,为实现材料非线性,钢材采用双线性随动强化(BKIN)的理想弹塑性材料,屈服准则采用Von Mises屈服准则。主桥钢结构除部分中支点处下弦杆采用Q390D钢材外其余均采用Q345D钢材;桥面板采用C50的混凝土;吊杆为强度等级为1 770 MPa的φ7成品高强钢丝,规格为PES7-109;柔性系杆采用强度等级为1 860 MPa的56φ15.24钢绞线。扣塔除立柱和横联采用Q345B的钢材外,其余立柱剪力撑均采用Q235B钢材;扣索和背索采用φ15.24低松弛钢绞线,每桁均由2组140φ15.24钢绞线组成。
钢桁拱桥考虑施工阶段的有限元模型如图2所示,共有个13 567节点,共10 732个单元。另外,成桥状态下拱桥纵梁边界条件布置图如图3所示。

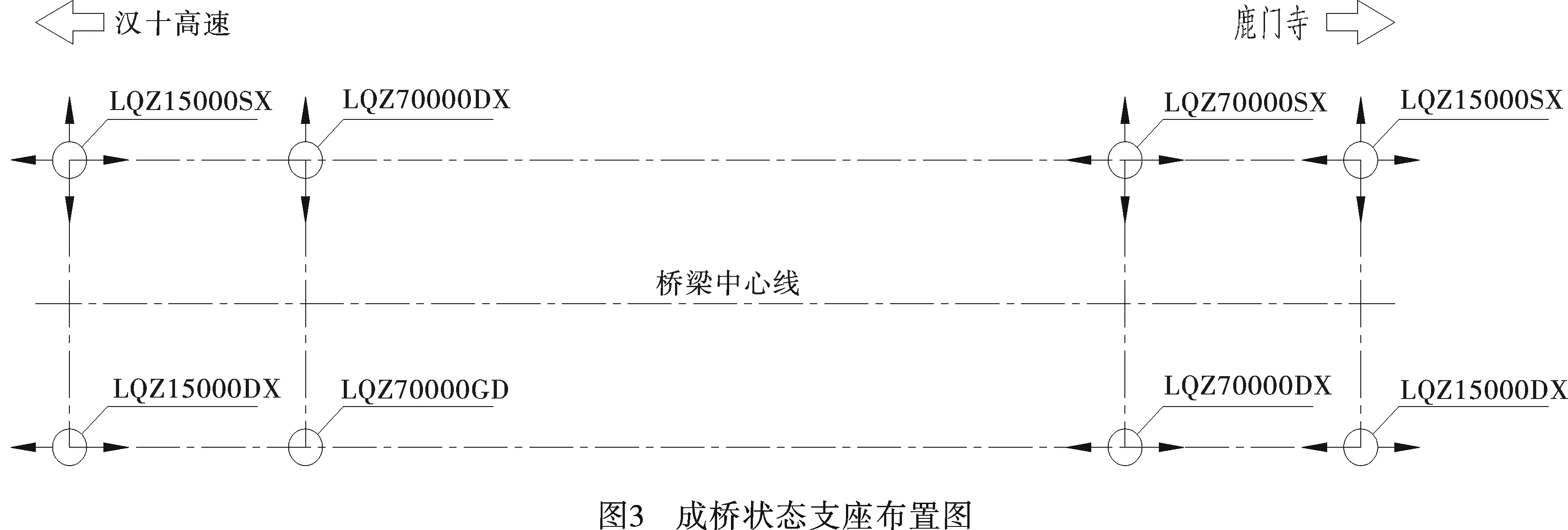
2.3 结果分析
稳定性分析也即屈曲分析,屈曲分析是一种用于确定结构在外荷载作用下开始变得不稳定时的临界荷载值和屈曲结构发生屈曲响应时的模态形状的技术。屈曲分析包括线弹性屈曲分析和非线性屈曲分析,线弹性屈曲分析在ANSYS软件中对应特征值屈曲分析,非线性屈曲分析也即考虑几何非线性和材料非线性双重非线性的极限承载力分析。特征值屈曲分析的理论前提是材料始终处于线弹性阶段,结构变形处于小挠度范围内,只适用于理想结构,求解结果偏安全,但也有其工程意义,此外,其求解结果为极限承载力分析提供了荷载理论上限,对后续非线性屈曲分析的荷载取值具有指导意义,因此对结构进行线弹性稳定分析也很有必要。
2.3.1 一阶稳定性在ANSYS中分析方法
特征值屈曲分析求解结果包括λ和{u},即为荷载系数和屈曲模态,在软件中实施的具体步骤如下:
1)静力分析
进入静力分析求解类型,打开预应力效应,PSTRES,ON,施加荷载进行求解;
2)模态分析
重新进入求解模块,选择模态分析类型,指定屈曲分析选项,求解完成,进入后处理模式。
2.3.2 恒载及安装荷载下的一阶稳定性
施工过程中除了主体结构及临时结构自重和拉索内力外,中跨拱肋合龙前还存在边跨压重,通过ANSYS有限元软件对钢桁拱桥施工过程中4个特定工况在恒载和安装荷载作用时的弹性稳定性进行分析,得出如下结果,见表1。

表1 各工况下恒载和安装荷载一阶稳定系数
注:表中稳定系数λ=极限荷载/单倍荷载。
考虑恒载和安装荷载作用各工况下失稳模态如图4所示。

从分析结果可以看出,吊索扣塔安装前稳定安全系数较高,失稳形态主要表现为桁架腹杆局部失稳;安装吊索扣塔后,拆除边跨的临时支架,随着中跨节段的拼装,荷载不断加大,此时结构失稳表现为吊索塔架面外压弯屈曲;随着中跨荷载不断加大,稳定安全系数不断减小,安装至主梁合龙段时,结构的失稳安全系数降至10.26;吊索塔架拆除后,卸载边跨压重,成桥状态在恒载作用下的安全系数达到9.81,失稳形态表现为主拱面外反对称失稳。总之,在恒载和安装荷载作用下,施工过程中及成桥状态的稳定性系数均较高。
3 结 论
a.静风荷载一阶稳定系数值均较大,可以看出施工过程及成桥状态时整体抗风性能良好,结构抗风可靠度较高;
b.各工况下失稳模态均表现为第一道风撑平联杆件面外的局部失稳,对于高耸的扣塔而言抵抗侧向风安全性能良好,拱肋合龙前,随着悬臂长度不断增加,拱肋的横向风荷载稳定安全系数不断减小,随着拱肋和主梁的合龙,侧向刚度增大,稳定系数略有增大。
[1] 姜礼尚.有限元方法及其理论基础[M].北京:人民交通出版社,1980.
[2] 梅建松.大跨度钢拱桥稳定性及极限承载力的研究[D].武汉:武汉理工大学,2005.
[3] 李国豪.桥梁结构稳定与振动[M].北京:中国铁道出版社,2003.
[4] 王勖成.有限单元法[M].北京.清华大学出版社,2003.
[5] Bathe K J,Bolourchi.Large Displacement Analysis of Three Dimensional Beam Structures[J].International Journal for Numerical Methods in Engineering,1979,14:961~986.
[6] 张洪伟.ANSYS非线性有限元分析方法及范例应用[M].北京:中国水利水电出版社,2013.
[7] Ever J Barbero.Finite Element Analysis of Composite Materials[M].Boca Raton:CRC Press,2007.
[8] 盖卫明.大跨度钢桁拱桥的稳定与极限承载力研究[D].长沙:中南大学,2009.
[9] 刘 剑,刘永健,杨炳成.关于桥梁结构线弹性稳定安全系数的谈论[J].广西大学学报:自然科学版,2009,34(6),719-724.

