智能汽车避障风险评估及轨迹规划*
王斌
(无锡商业职业技术学院,无锡 214153)
1 前言
交通事故的原因是多方面的,其中违反交通规则导致的交通事故占主导地位[1]。无人驾驶汽车严格遵守交通规则,反应时间极短,可根据路况规划最优路径,为减少甚至避免交通事故提供了新思路。
无人驾驶汽车的避撞系统由环境感知、轨迹预测、风险评估、轨迹规划、轨迹跟随等过程构成,其核心部分是危险评估和轨迹规划。风险评估指根据交通车(本文中指道路上其他车辆)驾驶意图和本车状态对碰撞危险进行评估,决定本车避撞行为(转向、制动、保持状态等),根据其原理,风险评估可分为基于车辆状态的风险评估[2]、基于驾驶意图的风险评估[3]、基于交互的风险评估[4]等。轨迹规划指根据交通车等障碍物的分布情况和状态,为本车规划出符合动力约束的避撞轨迹,根据原理不同,轨迹规划可以分为基于特定函数的轨迹规划[5]、基于搜索的轨迹规划[6]、基于优化的轨迹规划。
本文将汽车的确定性轨迹和概率性估计相结合,在确保风险评估真实性的同时提高了风险评估速度,提出了改进的快速搜索随机树算法,能够规划出平滑的安全避撞轨迹。
2 碰撞风险评估
碰撞风险评估主要包括驾驶员意图识别、汽车轨迹预测和碰撞概率检测。驾驶员意图识别内容复杂,不是本文研究的重点,因此在本文中假设驾驶员意图已知。
2.1 汽车轨迹预测
基于汽车状态的轨迹预测方法在短时间内精度很高,但是预测时间长的情况下误差很大甚至完全错误;基于驾驶员意图的轨迹预测方法在长时间内精度较高,短时间预测敏感度不高。因此本文将两种方法进行融合。
2.1.1 基于汽车状态的轨迹预测
基于汽车状态的轨迹预测包括运动学和动力学两种,本文使用运动学模型。常用的运动学模型包括恒速模型、恒加速模型、恒角加速度模型等。对于本车,本文选用恒角加速度模型;对于交通车,使用本车传感器能够测得交通车的位置、角度和速度,因此交通车选用恒加速模型。使用本车的车载传感器测量本车和交通车的运动状态,即可基于汽车状态对车辆轨迹进行预测。
2.1.2 基于驾驶员意图的轨迹预测
驾驶员的驾驶意图可以分为车道保持和换道两种,两种驾驶意图的轨迹预测原理相同,但是换道时的轨迹预测相对复杂。由文献[7]可知,五次多项式可以很好地拟合汽车的换道曲线,首先建立求解换道曲线的坐标系:以本车所在位置为坐标原点,以本车当前速度方向为X轴正方向,如图1所示。

图1 汽车换道轨迹
记目标车道曲线为y=ax2+bx+c,换道轨迹曲线为y=a5x5+a4x4+a3x3+a2x2+a1x+a0。记当前汽车纵向速度为vx,横摆角速度为w,换道曲线与目标车道线相切点为(xD,yD),则根据初始点和目标点的约束条件,解得。其中,式中,xD取不同值时预测结果也不同,如图2所示。
图2给出的汽车换道轨迹中,曲率过大时不满足汽车动力学约束,曲率过小时换道持续时间过长,与实际情况不符。考虑汽车的动力学约束、换道时间和最小转弯半径约束就可以去除所有可能换道轨迹中与实际不符、无法满足要求的轨迹,对剩余轨迹,建立指标函数进行评价:
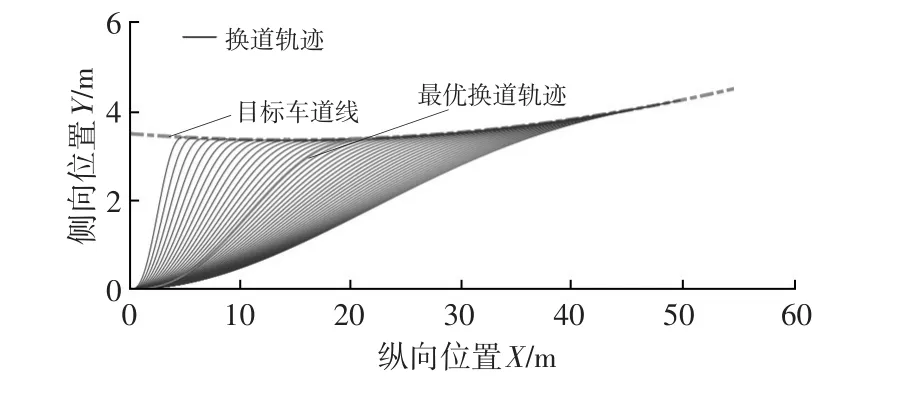
图2 可能的汽车换道轨迹

式中,aytra为轨迹tra的侧向加速度;aym为所有满足约束条件轨迹中最大的侧向加速度;ltra为轨迹tra的长度;lm为所有满足约束条件轨迹的最大长度;Δtra为汽车已行驶轨迹与换道轨迹的偏差;Δm为最大偏差;w1、w2、w3分别为3个因素的权重系数。
根据式(1)在权重相等条件下选择的最优路径见图2。
当本车行驶区域发现障碍物时,首先判断当前行驶状态是否安全,若安全则继续行驶,否则进行换道和制动的评估:优先选择制动,若制动无法满足安全要求,则搜索安全换道轨迹或低风险换道轨迹进行换道,最优轨迹即为前文介绍的轨迹;若不存在安全换道轨迹,则考虑换道同时制动,此时最优轨迹仍为前文预测的轨迹;若换道同时制动依然危险,则选择紧急制动,此时为车道保持情况。
2.1.3 基于驾驶员意图的轨迹预测
基于汽车状态的轨迹预测ym在短时间内精度很高,而基于驾驶员意图的轨迹预测yb在长时间时保持较高精度,因此本文使用加权融合的方法将两者轨迹预测方法融合在一起,即yf=w(t)ym+(1-w(t))yb,其中w(t)为权重函数,由于在1 s内ym精度高而1 s后ym精度严重下降,因此w(t)取为随三次样条曲线变化的值,如图3所示。

图3 权值变化曲线
2.2 碰撞概率计算
为了确保碰撞风险评估的真实性,本文考虑了汽车行驶的不确定性因素。
为了节省碰撞风险判断时间,首先进行确定性判断,若本车和交通车距离大于安全临界距离,则两者之间绝对安全,若本车和交通车距离小于危险临界距离,则两车发生碰撞,此两种情况都无需进行非确定性判断。若本车和交通车的距离处于两者之间时进行非确定性判断,计算各种避撞措施下的碰撞概率。
在纵向上,纵向距离大于车宽就不会发生碰撞,因此纵向只定义危险临界距离Δddan,此距离由车宽决定,是一个定值。在横向上,安全临界距离ΔLsaf由汽车当前速度vi决定,即ΔLsaf=1.2vi,危险临界距离ΔLdan由车身长度Ls决定,即ΔLdan=Ls。当本车与交通车距离在两者之间时考虑非确定因素。
结合本文使用的动力学模型,给出非确定性非线性系统的推导过程,即对于非线性系统(其中w(t)为高斯白噪声),将其线性化并离散化,得

式中,为恒角加速度模型的雅克比矩阵为k时刻系统状态均值;Σk为k时刻系统状态标准差。
记初始时刻的状态为则k时刻的状态可以由式(2)得到。换道时含有不确定因素预测的轨迹如图4所示。

图4 含不确定因素的预测轨迹
在任意时刻,已知两物体位置的统计特性就能够计算它们的碰撞概率。记本车位置和航向角为Xv=(xv,yv,φv),交通车位置和航向角为X0=(x0,y0,φ0)T,本车和交通车预测轨迹包络区域分别为Sv和S0。使用概率密度函数计算两车碰撞概率,记Xv、X0的高斯概率密度函数分别为pv(x,y,φ)、p0(x,y,φ),则碰撞概率为[8]:

使用蒙特卡洛模拟法对上式进行求解,得到其解为:

式中,n为数据的采样点个数,Ic(Svi,Soj)为自己定义的函数,其表达式为即当两区域Sv、So有重合区域时,此函数值为1,当两区域不重合时,此函数值为0。
3 道路避障行为决策
本文的道路避障决策从安全性方面考虑,选取车道行驶和交叉路口行驶两种典型的工况进行分析。
3.1 车道行驶避障行为决策
在车道行驶时,驾驶行为包括保持当前状态、制动、紧急制动、换道、换道同时制动,智能汽车的驾驶行为决策根据周围环境实时改变,即换道过程中可以采取制动措施,因此,驾驶行为可以分为保持当前状态、制动、紧急制动、换道。选择驾驶行为的前提是进行危险等级划分。图5所示情景为典型的交通场景,以此为例进行危险等级划分。
本车保持当前状态与Veh1、Veh2、Veh3发生碰撞的概率分布分别记为Pk1、Pk2、Pk3,本车换道与3辆车的碰撞概率分别记为Ps1、Ps2、Ps3,本车紧急制动与3辆车的碰撞概率分别记为Pb1、Pb2、Pb3,本文需要计算本车与交通车在一段时间的碰撞概率,因此以上概率均表示一个数据序列。记Pkmax=max(max(Pk1),max(Pk2),max(Pk3)),Pbmax、Psmax具有相同定义,Pcolls、Pcolld分别为碰撞概率的下限和上限阈值,则汽车危险等级划分为:若Pkmax<Pcolls,此时汽车是安全的,取Pcolls=0.2;若Pkmax>Pcolld,此时汽车是危险的,取Pcolld=0.6;若Pkmax在两者之间,汽车是不安全的。
根据当前汽车的危险等级制定避障措施,决策过程如图6所示。

图6 车道行驶驾驶行为决策
3.2 交叉路口避障行为决策
在交叉路口,交通路况复杂,应按照红绿灯指示进行行为决策,若没有红绿灯则使用保守的避障决策,本文以双向四车道交叉路口为例,如图7所示,本车与交通车的轨迹冲突情况如表1所示,其中“冲突”指交通车和本车在此意图下轨迹会发生冲突,要进行避障轨迹规划,“不”指车辆轨迹不冲突,可按当前状态继续行驶。

表1 交叉路口轨迹冲突判断
首先判断是否有交通车接近交叉路口,若有则判断轨迹是否冲突,不冲突时按当前状态前进,若冲突,则判断交通车到达路口时间和本车通过路口时间是否满足阈值。记所有交通车最先到达路口时间为Tarr,本车通过路口时间为Treq,若Tarr>Treq+1 s则不考虑交通车,本车按当前状态行驶,若不满足时间阈值条件,则判断本车采取制动或是换道措施,判断方法与车道行驶时一致。
4 避障轨迹规划
本文使用改进的快速搜索随机树算法进行最优避障路径的规划。
4.1 避障规划对快速搜索随机树算法的要求
快速搜索随机树算法是1998年提出的[9-10],结合智能汽车避障轨迹规划,快速搜索随机树算法存在以下缺陷:节点搜索完全随机,形成的轨迹震荡大、平滑性差,可能难以满足汽车动力学要求;节点搜索的完全随机性使算法收敛速度慢,难以满足避障路径规划的时间要求;轨迹规划的随机性使相邻周期内规划出的轨迹存在偏差,使汽车发生抖动。
汽车的轨迹规划对算法要求为:智能汽车通过传感器对周围环境识别,识别范围内障碍物数量有限;本车面对的障碍物主要是高速动态的交通车;轨迹规划实时更新,必须考虑算法的收敛时间;规划得到的轨迹要满足汽车运动学和动力学约束。
4.2 改进的快速搜索随机树算法
针对算法缺陷和汽车轨迹规划的要求,本文从多个方面对快速搜索随机树算法进行了改进。
引入目标偏向策略。由于快速搜索随机树算法使用的是节点随机搜索,为了提高算法收敛速度,本文使用此方法增加目标点的采样概率。此策略从算法开始即使用五次多项式判断初始点xinit与目标点xgoal之间是否存在可行轨迹。若存在且轨迹不经过障碍物和危险区,则将轨迹离散点添加到随机树上,轨迹规划完毕;若轨迹经过障碍物或危险区,则将障碍物前的轨迹离散点添加到随机树上,对每一个新增的节点xnew重复上述操作,直至找到目标点,这种轨迹搜索方式,不仅提高了算法的收敛速度,而且可以保证轨迹的平滑度。
改进节点连接策略。节点连接就是找出合适的节点xnear与产生的采样节点xrand连接,传统的快速搜索随机树算法根据距离最短选择节点xnear,但是在汽车轨迹规划中要考虑汽车的转向能力,要求采样节点xrand与xnear及xnear父节点夹角为钝角,基于此,将节点连接策略改进为:找出与采样点xrand距离最近的5个节点xnear,依据距离依次判断夹角是否满足条件,选择首先满足角度要求的点作为xnear,若均不满足则选择夹角最小的节点作为xnear,而后找到xrand关于xnear的对称点作为新的采样点。
引入节点修剪策略。节点修剪即删除可行轨迹中的多余节点,达到减少轨迹波动的目的。在随机树上找到从初始点到目标点的节点序列后,从初始点开始依次连接后续节点,若连接线不经过障碍物,则它们之间的节点可以删除,当经过障碍物时,则以碰撞点的父节点为新起点重复上述修剪过程。节点修剪完毕后判断节点间角度是否为钝角,若不满足角度要求,则通过增加节点满足角度要求。
轨迹平滑性方法。快速随机树方法得到的轨迹为折线,所以本文使用B样条曲线对节点进行拟合得到平滑的轨迹。B样条曲线具有以下特性:n阶B样条曲线具有(n-1)阶连续性,所以曲线平滑性好,适用于汽车轨迹;增加或减少1个节点,只对(n+1)段曲线产生影响,便于轨迹的局部修改;B样条曲线可构造满足过定点并与指定曲线相切的要求。B样条曲线的以上特性使其能够拟合出平滑轨迹,并符合汽车运动学和动力学要求。试验发现,5阶B样条曲线更适合拟合汽车轨迹[11]。
最优轨迹的选择。一般情况下,规划出的避障轨迹有多条,考虑轨迹的安全性、可实现性及其长度,轨迹安全性通过其与障碍物的距离表征,可实现性考虑轨迹的侧向加速度,基于上述3个方面给出选择最优轨迹的评价指标:
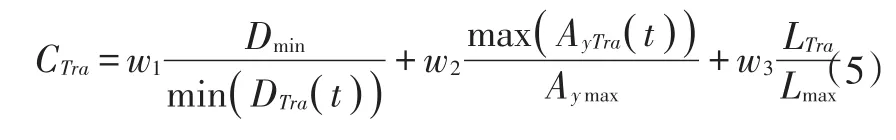
式中,Dmin为所有轨迹与障碍物的最短距离;DTra(t)为轨迹Tra与障碍物的距离;AyTra(t)为轨迹Tra的侧向加速度;Aymax为所有轨迹中侧向加速度的最大值;LTra为轨迹Tra的长度;Lmax为所有轨迹中长度的最大值;本文取w1=w2=1,w3=0.5。
轨迹的实时规划。汽车行驶环境是高度变化的,且轨迹规划的长度非常有限,因此轨迹规划需要实时更新。在轨迹更新时,为了充分利用上一周期的规划结果,保留当前最优轨迹的下一节点作为新周期根节点的子节点,并保留此节点到达目标的所有节点。若此轨迹依然对新周期适用,则继续按此轨迹行驶;否则放弃导致碰撞的节点,重新进行轨迹规划。
轨迹跟随控制,就是要求汽车精准地按照规划的轨迹行驶,常用的轨迹跟随控制方法有最优预瞄控制、模型预测控制,从算法复杂度和控制效果看,本文选用最优预瞄控制方法,具体原理可参考文献[12]。
5 仿真验证
5.1 仿真介绍
本文使用的仿真软件为PanoSim,为了对避撞和轨迹规划方法进行验证,本文设计了干扰换道工况和交叉路口工况。
在计算预测轨迹不确定性时,需要知道本车和交通车的协方差矩阵,根据传感器精度及现有研究成果,本车初始协方差阵为08×8,交通车协方差阵为diag(0.52,0.52,0.22,0.22,0.22,0.22)。
5.2 仿真结果分析
干扰换道工况:本车行驶速度为50 km/h,前方60 m处交通车Veh1以20 km/h行驶,相邻车道Veh2在本车前20 m以30 km/h行驶,行驶到1.4 s时本车预测到以当前状态行驶不安全(Pcoll=0.224),此时换道或紧急制动均不危险,按照换道优先原则,此时进行换道轨迹规划如图8a所示,本车换道中4.4 s时Veh1突然紧急换道并略有加速,本车按此时状态前进会发生危险,如图8a所示,图中本车与Veh1轨迹发生交叉且时间无法错开。
通过对紧急制动和换道进行危险评估,本车发现采用换道同时以-1 m/s2减速可以避开Veh1、Veh2,得到Veh1、Veh2、本车最终的预测轨迹如图8b所示。
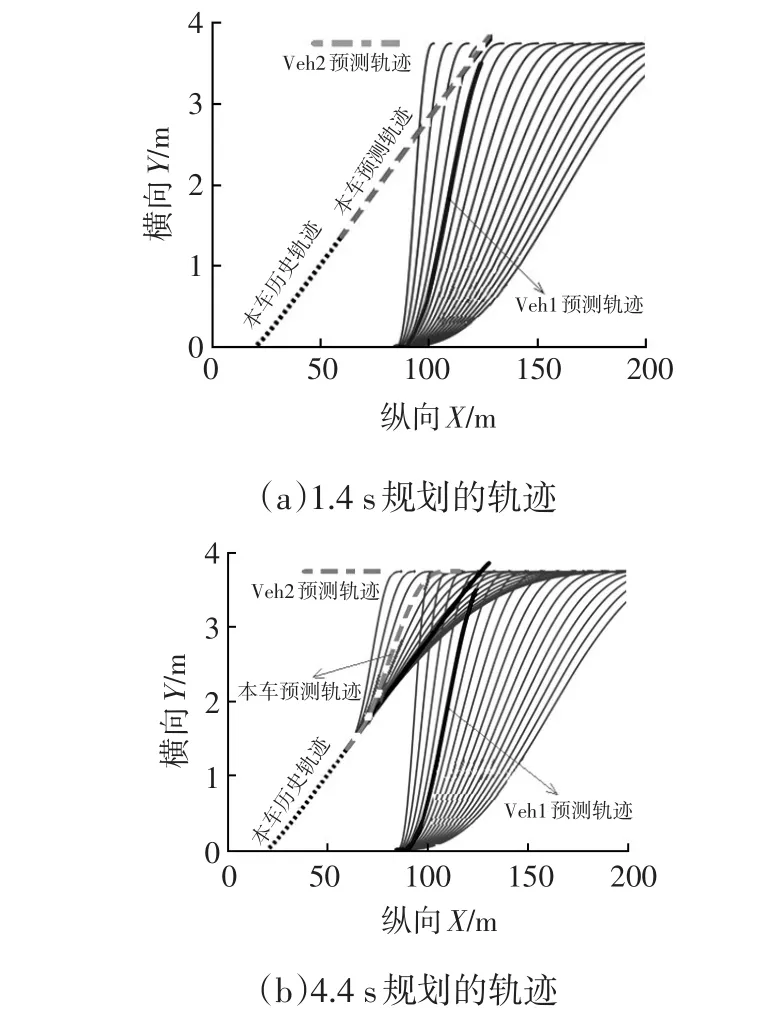
图8 干扰换道仿真结果
从以上仿真结果可以看出:本车能够根据交通车驾驶意图准确预测其他交通车辆的运动轨迹;结合确定因素和非确定因素,本车能够及时判断出危险等级;当车辆不安全或危险时,本车能够采取适当措施(制动或换道)并进行轨迹规划,及时避开障碍物。
交叉路口工况:本车以30 km/h速度在交叉路口左转,交通车以30 km/h直线行驶,以当前状态行驶,本车和交通车在离开交叉路口时会发生碰撞,如图9a所示。本车采用制动方式(加速度-1 m/s2)进行避障,碰撞概率、最优轨迹规划如图9b、图9c所示。
从图9b可以看出,本车在行驶过程中,当与交通车的碰撞概率上升到不安全阈值时,汽车采取避障措施,措施有效,使得碰撞概率下降,汽车风险等级回到安全状态,所以图中的碰撞概率先上升后下降。


图9 交叉路口仿真结果
由以上两种工况的仿真结果可以看出,本文提出的智能汽车风险评估及避障轨迹规划方法能够准确预测交通车轨迹,结合确定因素和不确定因素准确判断出风险等级,能够及时找出合适的避障措施并进行轨迹规划,规划出的轨迹安全、平滑,满足汽车运动学和动力学约束。
6 结论
本文将汽车状态和驾驶意图相结合预测交通车轨迹,保证了轨迹的短期和长期精度;同时考虑汽车碰撞的确定性因素和不确定因素,保证了风险评估的准确性和快速性;给出的道路行驶和交叉路口避障行为决策策略准确有效,可以避免碰撞发生;使用改进的快速搜索随机树算法能够快速规划出一条最优路径,此路径符合汽车运动学和动力学约束。
[1]胡启洲,高宁波,叶茂.基于支持向量机的道路交通事故数据统计模型研究[J].中国安全科学学报,2013,23(6):39.
[2]Zhang Y,Antonsson E K,Grote K.A new Threat Assessment Measure for Collision Avoidance Systems[C]//Intelligent Transportation Systems Conference,2006.IEEE,2006:968-975.
[3]郑华荣.考虑周边车辆驾驶意图的换道危险预警研究[D].武汉:武汉理工大学,2013.
[4]Lawitzky A,Althoff D,Passenberg C F,et al.Interactive Scene Prediction for Automotive Applications[C]//Intelligent Vehicles Symposium.IEEE,2013:1028-1033.
[5]Ren D B,Zhang J Y.Trajectory Planning and Yaw Rate Tracking Control for Lane Changing of Intelligent Vehicle on Curved Road[J].Science China Technological Sciences,2011,54(3):630-642.
[6]刘多能.基于人机智能融合的移动机器人路径规划方法研究[D].长沙:国防科学技术大学,2011.
[7]Yao W,Zhao H,Davoine F,et al.Learning Lane Change Trajectories from On-road Driving Data[C]//Intelligent Vehicles Symposium.IEEE,2012:885-890.
[8]Stellet J E,Schumacher J,Branz W,et al.Uncertainty Propagation in Criticality Measures for Driver Assistance[C]//Intelligent Vehicles Symposium.IEEE,2015:1187-1194.
[9]徐联杰,刘检华,何永熹,等.一种基于改进快速搜索随机树算法的管路自动布局方法[J].图学学报,2016,37(1):1-10.
[10]莫栋成,刘国栋.改进的快速探索随机树双足机器人路径规划算法[J].计算机应用,2013,33(1):199-201.
[11]任重,杨灿军,陈鹰.轨迹规划中的B样条插值算法[J].机电工程,2001,18(5):38-39.
[12]沈峘,凌锐,李舜酩,等.基于预瞄最优曲率模型的大曲率转向控制方法[J].中国机械工程,2012,23(17):2111-2116.

