“8”字绕障无碳小车微调机构的设计＊

王 帅，苏航杰，武振宇，徐凌峰

（天津科技大学机械工程学院，天津 300457）

“8”字绕障无碳小车设计比赛是全国大学生工程训练综合能力竞赛的比赛项目之一，迄今已经举办了五届。无碳小车为了补偿加工和安装误差，实现精确的轨迹要求，必须设计一套可靠的微调机构，这是无碳小车设计的难点之一。从以往的比赛情况来看，很多无碳小车都能够完成特定桩距的“8”字形轨迹路线，但一旦桩距发生改变，很多小车便不能按照精确设计好的路线行驶，导致绕桩失败。

1 对轨迹偏移的分析

图1是“8”字绕障无碳小车的理想轨迹。该轨迹由4个部分组成，其中，AB和CD由过渡曲线组成，BC和DA由圆弧组成；AB与CD的交点为O，定义为轨迹中心；圆弧DA的圆心为O1，圆弧BC的圆心为O2。如果小车能够重复不断的、无偏移的沿该轨迹运行，则绕桩成功。

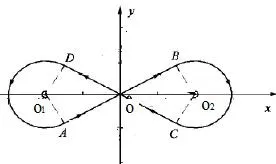
图1 “8”字绕障无碳小车理想轨迹

图2 小车转弯时的运动状态

为了分析小车轨迹出现偏移的原因，建立了无碳小车的数学模型。小车为三轮对称结构，前轮为转向轮，前轮转角可以实现周期偏转；后轮为驱动轮，左右两侧车轮由同一根轴驱动，轴上装有差速器。小车前后轴距L为12 mm，后轮轮距B为13 mm，取后轮距中心点P为参考轨迹点，则小车在转弯时的状态如图2所示[2]。

图2中，θ为小车转弯时前轮转角。设小车左转时前轮转角为θ1，小车右转时小车转角为θ2，则小车每完成一个“8”字轨迹，前轮的总转角β＝θ1＋θ2。如果小车轨迹对称，则θ1＝θ2，给定桩距就可计算出θ值。设桩距等于400 mm，则计算出θ1＝θ2＝28.68°[3]。

将前轮转角赋予不同的数值，利用MATLAB软件对所建立小车模型的运行轨迹进行模拟仿真发现，当θ1＝θ2且θ1与θ2之和即前轮总转角β与理论值相等时，小车沿理想“8”字轨迹运行；当θ1≠θ2且θ1与θ2之和与理论值相等时，小车沿偏移轨迹运行；当θ1＝θ2且θ1与θ2之和与理论值不相等时，小车沿偏移轨迹运行；当θ1≠θ2且θ1与θ2之和与理论值不相等时，小车沿偏移轨迹运行。

图3 双螺旋微调机构

2 对微调机构的改进

小车轨迹出现偏移的主要原因是前轮总转角过大或过小，前轮左转和右转角度不相等造成。因此，微调机构必须具有能够调整总转角大小以及分配左右转角的功能。传统的无碳小车微调机构有滑块式机构、螺母式机构2种。螺母式机构没有刻度，调整无法量化；滑块式机构精度太小，调整起来困难比较大，且不能连续调整。这些调整机构均不能精确调整前轮总转角大小，分配左右转角。为此，本设计提出引入2套高精度的螺旋测微装置用于微调机构，1套用于前轮总转角调整，1套用于左右转角分配，如图3所示。

为了验证微调机构方案的正确性，制造了样车。经测试，通过对该样车传动系统和微调机构的调整，可以实现300～500 mm的绕桩行驶，并接近于理想的“8”字形轨迹。绕400 mm桩距时，平均可重复46圈。

3 结束语

本文对无碳小车运行轨迹的偏移进行分析，对微调机构进行创新设计。在试验调试中发现，微调机构中的2套高精度螺旋测微装置能够精准调整总转角大小，并分配左右转角，有效实现轨迹要求。这个设计能更好地达到比赛的要求。

［1］赵国博，赵保璇，潘瑞鹏.基于MATLAB的“8”字绕障无碳小车的轨迹模拟［J］.机械工程师，2017（1）：97-98.

［2］曹斌，张海波，朱华炳.基于槽轮机构的8字轨迹无碳小车设计［J］.合肥工业大学学报（自然科学版），2014，37（6）：661-665.

［3］任帅，高远，邵梦莹.8字无碳小车的结构设计［J］.科技创新导报，2017（18）：110-111.