基于子带谱间变换的多光谱图像压缩

王 平，陈 欣，粘永健，乔 梁

(1.重庆工程学院软件与计算机学院，重庆 400056； 2.陆军军医大学生物医学工程与影像医学系，重庆 400038)

0 引言

星载多光谱图像庞大的数据量给存储与传输带来了巨大挑战，只有采用高效的数据压缩技术对其进行压缩，才能在现有带宽条件下实现实时传输。无损压缩的压缩比较低，通常在2以内，难以满足实际的压缩需求。有损压缩通过引入一定的信息损失来获得较高的压缩性能，能够满足多光谱图像的数据存储与实时传输需求。此外，卫星上的计算资源和功耗都是极度受限的，这就对压缩算法提出了较高要求，所采用的有损压缩算法不但需要提供理想的压缩性能，而且必须具有较低的计算复杂度。

目前，多光谱图像的有损压缩方法主要包括基于预测的方法和基于变换的方法。由于基于预测的方法难以精确控制压缩码率，CONOSCENTI提出了相应的码率控制方案，并提出了几种熵编码方案用于提高算法的硬件运算效率[1]，然而，基于预测的有损压缩算法普遍存在着误码传递，性能不尽人意。基于变换的方法利用一维和二维变换分别去除谱间与空间相关性，在有损压缩中应用广泛。典型的变换方法包括卡胡南-洛维变换(KLT)、离散余弦变换(DCT)与离散小波变换(DWT)等。TANG利用DWT去除谱间相关性，提出了适用于多光谱图像压缩的三维分层树集合分裂(3D SPIHT)算法[2]，但由于DWT在去除谱间相关性上性能远不如KLT，这使得3D SPIHT算法的性能不尽人意。SHARMA比较了诸多基于三维变换的多光谱图像压缩算法，发现谱间一维KLT变换与空间二维DWT变换可以获得较高的压缩性能[3]。RUCKER在KLT与JPEG2000的压缩框架下，提出了3种码率分配方案，测试结果表明联合率失真压缩能够获得整体最优的压缩性能[4]。PENNA将异常检测引入到多光谱图像的有损压缩中，利用谱间KLT与空间JPEG2000的压缩方案，在压缩过程中对异常点进行特殊保护[5]。CARVAJAL提出了一种有损压缩与近无损压缩相结合的压缩算法[6]，该算法以有损压缩为主，近无损压缩作为有损压缩的补充。CAGNAZZO利用高效的分割算法把多光谱图像分割成不同的区域[7]，对每类区域分别进行光谱方向上的KLT，然后利用任意形状小波变换对每个主成分的不同区域分别进行空间变换，最后，对不同区域进行任意形状的SPIHT压缩。BITA首先对每个波段进行二维小波变换，然后对每个子带按照特定的顺序进行扫描，再对所有波段的对应子带进行谱间KLT，取得了较好的压缩效果[8]。针对KLT可能难以捕捉用于分类的判别信息，LEE预先编码特征信息，然后结合KLT变换实现多光谱图像压缩[9]。尽管KLT具有较好的去相关效果，但其复杂度较高。为此，PENNA提出了低复杂度谱间KLT变换[10]，通过对原始图像进行采样来计算KLT的协方差矩阵，虽然在一定程度上降低了复杂度，但损失了部分压缩性能。BLANES指出协方差矩阵的迭代分解是造成KLT复杂度高的主要原因，并提出了成对KLT变换用于去除谱间相关性，极大地降低了复杂度，但压缩性能也有所损失[11]。NIAN提出了一种无分组的成对KLT变换结构，显著降低了复杂度，但仍损失了部分压缩性能[12]。文献[13]提出了一种基于DWT和改进KLT的高效压缩算法，首先利用二维DWT在空间方向上进行变换，然后再进行不同基的KLT，实验结果表明该方法具有一定的压缩性能。文献[14]利用基于分块的KLT去除谱间相关性，引入配对KLT降低算法的复杂度，其不足是KLT块图像会同时包含不同层下的小波子带，在一定程度上影响去相关性能。针对以上不足，本文提出了基于子带谱间变换的多光谱图像低复杂度压缩算法，该算法结合成对KLT变换结构降低算法的复杂度，同时利用子带谱间KLT变换提高谱间去相关性能，与传统KLT压缩算法相比，在保证压缩性能的同时，有效降低了计算复杂度。

1 空间变换与谱间变换的选取

多光谱图像本质上是一个图像序列，序列中的每个波段都是同一个地物在特定波长上的成像。多光谱图像同时具有谱间相关性与空间相关性。因此，要获得理想的压缩性能，必须选取合理的变换方法去除谱间与空间相关性。

1.1 空间变换的选取

与全色图像相比，多光谱图像的空间相关性较低，这是由其较低的空间分辨率造成的，但在多光谱图像的压缩算法设计中，如何有效去除空间相关性，仍需要着重考虑。小波变换具有多分辨率分析的特性，能够与人眼的视觉特性相吻合，已经在图像压缩中获得了广泛的应用，这一点是DCT无法比拟的。因此，在空间相关性的去除上，本文采用性能较好的CDF9-7小波去除多光谱图像每个波段的空间相关性。

1.2 谱间变换的选取

KLT在多光谱图像谱间变换中获得了广泛应用，取得了远远优于DWT和DCT的去相关效果，其原因是KLT的基函数能够与图像特性较好地匹配。若多光谱图像包含L个波段，每个波段的高度为M、宽度为N、波段数量为L，则坐标为(m,n)(m=1,2,…,M;n=1,2,…,N)处的光谱向量表示为

(1)

(2)

其中

Cmn=E[(Xmn-V)(Xmn-V)T]

(3)

式中，V=[v1,v2,…,vL]T为均值向量。对C进行特征值分解可得特征值λl(l=1,2,…,L)和特征向量U=[u1,u2,…,uL]。在此基础上，谱间变换后的主成分图像为

Yij=UT(Xij-V)。

(4)

多光谱图像经过谱间KLT变换后，整个图像的能量会集中在少数几个特征值较大的主成分上。图像能量越集中，对后续压缩性能的提高越有利。

2 基于子带谱间变换的多光谱图像压缩

2.1 成对KLT变换

KLT应用于多光谱图像谱间去相关的传统方法是将KLT直接作用于多光谱图像的所有波段来完成谱间去相关。由于多光谱图像通常包含数个波段，这使得整个谱间KLT的计算量较大，其原因是对协方差矩阵的特征值分解需要不断地进行数值迭代。为了解决这个不足，BLANES提出了成对KLT变换[11]，并给出了在成对变换情况下特征向量矩阵U的直接计算方法，其主要思想是对多光谱序列进行两两分组，KLT分别对每组的两个波段进行谱间变换，这样可以避免特征值分解的迭代运算，有效降低了计算量。此外，文献[12]在上述算法基础上提出了一种串行成对变换结构，首先对多光谱图像的前两个波段进行谱间KLT变换，然后将特征值较大的主成分与后续相邻波段再次进行谱间KLT，依次变换直到最后一个波段。相比于BLANES提出的算法，该变换结构的优点是无需事先进行分组。从实验结果来看，与传统KLT相比，两种变换结构的压缩性能较为接近。本文采用无分组的串行变换结构，为了保证压缩性能，提出子带谱间KLT变换，主要目标是获得与传统KLT相当的压缩性能。

2.2 子带谱间KLT变换

多光谱图像每个波段进行二维小波变换后，图像会被分解成一系列高频子带和一个低频子带。其中,每一层小波变换后得到的3个高频子带分别代表了原图像不同方向上的高频成分，而最终得到的一个低频子带代表了原图像的低频成分。因此，不同层的子带拥有不同的统计特性，代表了不同的频率成分。在后续的谱间KLT变换过程中可以考虑针对不同的子带分别进行谱间KLT，从而充分利用不同子带的统计特性，提高谱间去相关性能。为了在成对变换的基础上提高压缩性能，借鉴文献[8]提出的算法思路，本文提出了基于子带谱间变换的多光谱图像压缩算法，该算法首先对每个波段分别进行二维小波变换，然后将每一层小波变换得到的所有高频子带看成一个整体，将最终的低频子带看成一个单独的子带。图1给出了一幅经过3层小波分解后的子带图像，如上所述，将具有相同标号的子带进行合并，图中共有4个合并后的子带，后续的谱间KLT就是在波段间相同空间位置的子带组合体之间进行。

图1 子带组合示意图Fig.1 Diagram of sub-band combination

针对每一个合并后的子带，在光谱方向上进行成对KLT变换，以此去除多光谱图像的谱间相关性，从而得到空间与谱间去相关后的主成分。本文采用最优截断的嵌入式块编码(Embedded Block Coding with Optimized Truncation,EBCOT)对所有的主成分同时进行联合率失真压缩[15]，从而获得全局最优的压缩性能。整体的压缩流程如图2所示。需要指出的是，每个合并子带进行成对KLT变换所得到的特征向量矩阵都需要作为附加信息传输到解码端用于KLT反变换。

图2 本文提出的算法流程Fig.2 Flow chart of the proposed algorithm

3 实验结果与分析

为了验证所提算法的有效性，采用法国SPOT-Vegetation探测器与美国IKNOS卫星获取的多光谱图像作为实验图像，所有测试图像的波段数为4(红、绿、蓝与近红外)，每个波段像素大小为1024×1024，每个像素占用2个字节。

3.1 压缩性能比较

采用码率每波段每像素的比特数(bit per pixel per band,bpppb)和信噪比(SNR)评价压缩算法的性能。本文提出的算法在光谱方向上对每个子带组合体分别进行谱间KLT变换。因此，小波变换的层数会影响合并后的子带数量，进而影响谱间去相关效果。图3分别给出了SPOT和IKNOS图像在不同的小波分解层数情况下的压缩性能，可以看出，随着小波分解层数的增加，压缩性能逐步得以提高，其原因是小波分解层数越多，能量就越集中，但当小波分解层数过高时，最终得到的低频子带就越小。在后续的EBCOT编码中，通常会将小波变换后的图像分成像素大小为32×32的块，然后以块为单位进行率失真压缩。因此，低频子带的合理像素大小应为32×32或者64×64。

图3 小波分解层数对压缩性能的影响Fig.3 The effect of wavelet decomposition levels on compression performance

从图3可以看出，4层小波分解与5层小波分解所得到的压缩性能几乎相当，因此，从降低计算复杂度的角度考虑，4层小波分解是合理的选择。

为了验证算法的有效性，将本文算法与基于传统KLT的压缩算法以及低复杂度KLT压缩算法(ρ=0.001)[10]的压缩性能进行比较，如图4与图5所示。对于星载多光谱图像，其后续应用主要集中在分类与目标检测方面[16-17]，为了保证图像质量，低码率压缩是不被允许的。因此，这里的码率bpppb取值范围设为1～3。

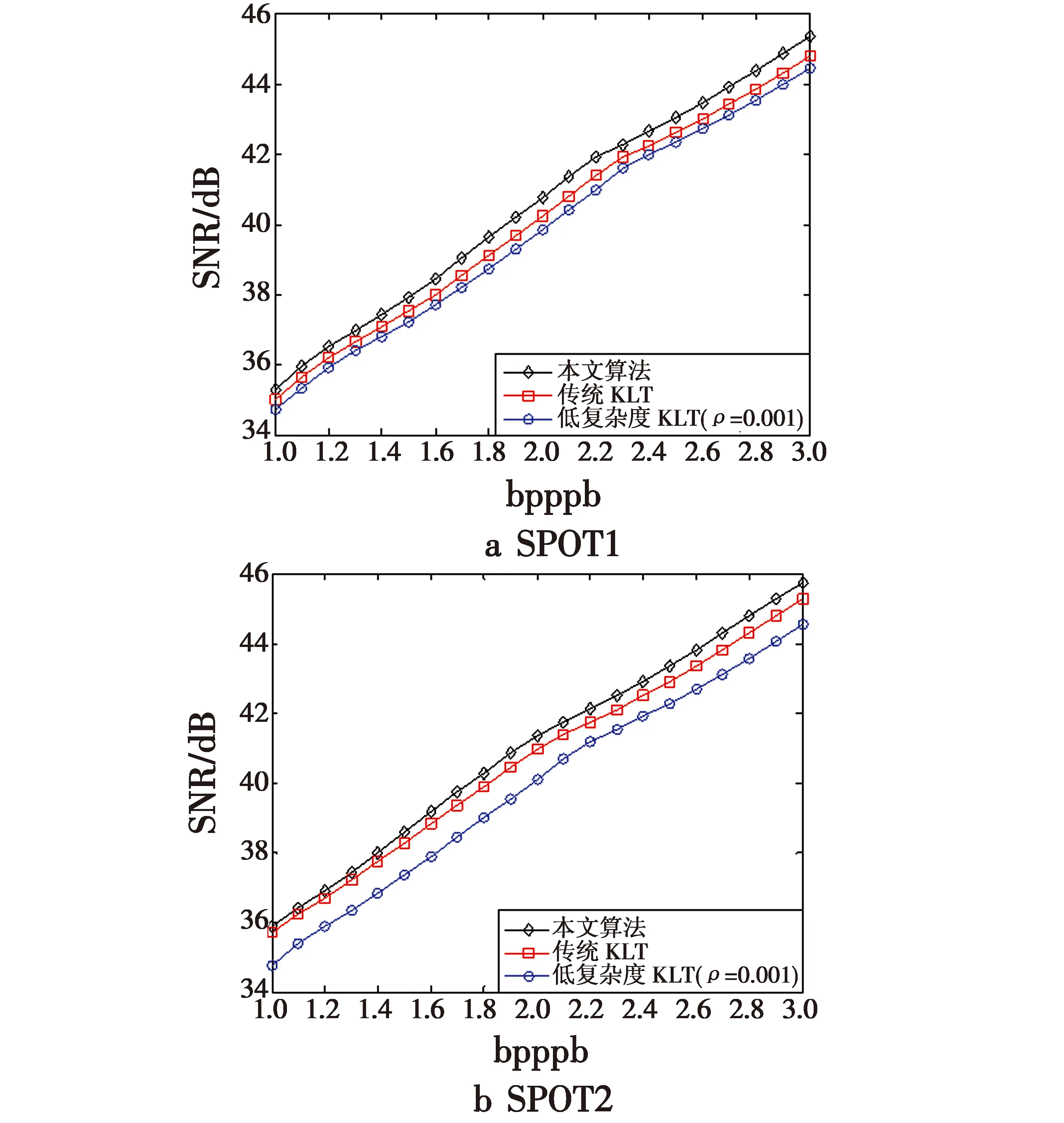
图4 SPOT卫星图像压缩性能比较Fig.4 Comparison of compression performance of SPOT satellite images

从图4可以看出，对于SPOT卫星多光谱图像，本文算法的压缩性能明显优于后两种算法。传统KLT压缩算法对整个图像整体进行谱间KLT变换，虽然取得了良好的压缩性能，但该变换方式无法利用图像的局部相关性，这使得基于KLT的压缩性能仍有提高的空间。低复杂度KLT算法通过对原始图像采样的方式降低协方差矩阵计算的复杂度，这使得协方差矩阵的估计产生误差，降低了算法的压缩性能，并且采样率越低(ρ越小)，压缩性能下降得越快。对于本文算法而言，虽然成对KLT会在一定程度上降低了压缩性能，但利用子带谱间变换去除多光谱图像的谱间相关性，能够在一定程度上利用多光谱图像的子带统计特性，进而提高谱间去相关的效果，从而弥补了成对变换带来的性能损失。

图5 IKNOS卫星图像压缩性能比较Fig.5 Comparison of compression performance of IKNOS satellite images

从图5可以看出，对于IKNOS卫星获取的多光谱图像，本文算法的压缩性能与整体KLT算法的压缩性能相当，并显著优于低复杂度KLT压缩算法。以上结果充分表明，本文算法的压缩性能不低于传统KLT压缩算法的压缩性能，并且显著高于低复杂度KLT压缩算法的压缩性能。

3.2 编码复杂度比较

表1给出了各种算法对每个波段的编码时间对比。从该表可以看出，JPEG2000由于未考虑去除多光谱图像的谱间相关性，使得其编码复杂度较低，但压缩性能不理想。与传统KLT算法相比，低复杂度KLT算法通过采样的方式估计协方差矩阵，虽然在一定程度上降低了编码复杂度，但这种复杂度的降低并不显著，原因是该算法并未解决协方差矩阵分解的迭代计算问题。本文算法采用成对变换的方式，避免了上述不足，编码时间显著低于传统KLT与低复杂度KLT，并且易于硬件实现。此外，本文算法每次只针对两个波段的对应组合子带进行谱间KLT变换，相比于传统KLT和低复杂度KLT，显著降低了计算内存需求。

表1 编码时间比较Table 1 Comparison of encoding time ms

4 结束语

针对星载多光谱图像压缩的需求，本文提出了一种基于子带谱间变换的多光谱图像有损压缩算法。该算法在空间二维小波变换的基础上，利用子带谱间KLT变换去除谱间相关性，通过成对变换的方式降低KLT的计算复杂度，结合JPEG2000中的EBCOT算法实现整体最优的率失真压缩。针对SPOT和IKNOS卫星多光谱图像的测试结果表明，该算法不但能够获得不低于传统KLT压缩算法的率失真性能，而且编码复杂度较低，适用于实现星载多光谱图像的高效压缩。

参考文献

[1]CONOSCENTI M,COPPOLA R,MAGLI E.Constant SNR, rate control,and entropy coding for predictive lossy hyper-spectral image compression[J].IEEE Transactions on Ima-ge Processing,2016,54(12):7431-7441.

[2] TANG X L,CHO S,PEARLMAN W A.Lossy-to-lossless block-based compression of hyperspectral volumetric data[C]//Proceedings of the IEEE International Conference on Image Processing,Atlanta,GA,America,2006：1133-1136.

[3]SHARMA S,DEWAL M L,ANAND R S.Performance evaluation of 3D hybrid transforms and 2D-set partitioning methods for lossy hyperspectral data compression[J].Signal,Image and Video Processing,2015,9(8):1881-1888.

[4] RUCKER J T,FOWLER J E,YOUNAN N H.JPEG2000 coding strategies for hyperspectral data[C]//Proceedings of the International Geoscience and Remote Sensing Symposium,Seoul,South Korea,2005:128-131.

[5] PENNA B,TILLO T,MAGLI E,et al.Hyperspectral image compression employing a model of anomalous pixels[J].IEEE Geoscience and Remote Sensing Letters,2007,4(4):664-668.

[6] CARVAJAL G,PENNA B,MAGLI E.Unified lossy and near-lossless hyperspectral image compression based on JPEG2000[J].IEEE Geoscience and Remote Sensing Letters,2008,5(4):593-597.

[7] CAGNAZZO M,POGGI G,VERDOLIVA L.Region-based transform coding of multispectral images[J].IEEE Tran-sactions on Image Processing,2007,16(12):2916-2926.

[8] BITA I P A,BARRET M,PHAM D T.On optimal transforms in lossy compression of multicomponent images with JPEG2000[J].Signal Processing,2010,90(3):759-773.

[9] LEE C,YOUN S,JEONG T,et al.Hybrid compression of hyperspectral images based on PCA with pre-encoding discriminant information[J].IEEE Geoscience and Remote Sensing Letters,2015,12(7):1491-1495.

[10] PENNA B,TILLO T,MAGLI E,et al.Transform coding techniques for lossy hyperspectral data compression[J].IEEE Transactions on Geoscience and Remote Sensing,2007,45(5):1408-1421.

[11]BLANES I,SERRA-SAGRISTA J.Pairwise orthogonal transform for spectral image coding[J].IEEE Transactions on Geoscience and Remote Sensing,2011,49(3):961-972.

[12] NIAN Y J,LIU Y,YE Z.Pairwise KLT-based compression for multispectral images[J].Sensing and Imaging,2016,17(1):1-15.

[13] 徐冬冬，付天骄，张宇.基于改进的K-L变换的多光谱图像压缩算法[J].光电子·激光，2015,26(6):1200-1205.

[14] 王平，陈欣，粘永健，等.基于分块KLT的多光谱遥感图像低复杂度有损压缩[J].红外技术，2018,40(2):151-157.

[15] TAUBMAN D.High performance scalable image compression with EBCOT[J].IEEE Transactions on Image Processing,2000,9(7):1158-1170.

[16] 吕俊伟，樊利恒，邓江生，等.基于聚类集成的半监督多/高光谱图像分类方法[J].电光与控制，2016,23(5):30-36.

[17] 廖佳俊，刘志刚，姜江军.基于改进双边滤波稀疏表示的高光谱目标检测算法[J].电光与控制，2017,24(7):37-40.