多无人机协同打击任务分配方法

陈 侠，乔艳芝

(沈阳航空航天大学，沈阳 110136)

0 引言

多机协同指的是多架无人机通过相互配合、协作的作战方式执行任务[1]，具有同时攻击多个敌方目标和能提高杀伤概率的优点。在多无人机执行任务的过程中，无人机之间的妥善协调问题是其可否成功完成任务的重要因素之一[2]。通过选择合理的决策策略使得多无人机之间相互协调完成复杂的任务,目前是无人机领域研究的热点问题[3]。近十多年来，这方面的研究已经取得了一些成果[4-11]。文献[4]以双层规划为基础，提出了无人机协同攻击目标分配模型；文献[5]对环境中威胁的描述比较简单，但是考虑了飞机能力的裕度约束，从而建立了多无人机任务分配模型；文献[6]在多机任务协调问题中引入了买卖合同机制。虽然关于多无人机协同任务分配的研究已经取得了一些研究成果，但在已有的文献中，建立的多机协同任务分配模型没有考虑多无人机协同打击的能力问题，也没有考虑目标需要获得被打击的能力值问题，计算航程代价均考虑始发点与目标点之间的航程，并没有考虑无人机发射导弹的航程，建立的多无人机作战模型还不是很完善。而在多机器人任务分配中，考虑机器人能力函数的研究成果吸引了越来越多学者的关注[12-13]，文献[12]将效用函数应用于多机器人系统任务分配策略中；文献[13]提出了一种基于机器人效用函数的多机器人系统任务分配新方法。但迄今为止，关于多无人机协同打击能力的任务分配问题尚无文献报道。本文通过建立无人机的能力函数及其雅可比矩阵，给出了多无人机协同打击位置和无人机俯仰角的计算方法，提出了多无人机协同打击任务的动态任务分配方法，仿真结果表明：考虑多无人机协同打击能力的任务分配与未考虑的分配方案相比，可获得更大的目标收益值，提高了多无人机协同打击能力。

1 无人机协同能力函数的建立

能力函数指的是根据无人机所执行任务的主要要求和形式对目标释放的能量建立的具体量化函数。在无人机执行侦察和攻击任务时，为了最大可能地发挥作用，无人机与目标之间的距离、方位和所携带武器的发射距离、方位等都需要重点考虑。所以，建立的能力函数与距离和方位等因素都有关系，将单无人机的能力函数相加就是群无人机的能力函数。为方便计算，只考虑无人机与目标点之间的距离和角度两个因素，当无人机与目标点的距离和角度都满足要求时，无人机就能释放最大的能力。将无人机的位置信息和目标点信息分别存储在n×3和m×3矩阵中，n和m分别为无人机和目标的数量。无人机与目标的初始位置矩阵为

(1)

无人机i与目标j的距离dij描述为

(2)

如图1所示，建立地面坐标系，坐标原点为O，U为无人机，U′为无人机在XOY平面的投影，T为目标，无人机的视线和U′与目标连线的夹角θij(俯仰角)描述为[14]

(3)

假定能力函数的最大值为1,目标j获得无人机的能力函数Bi为

(4)

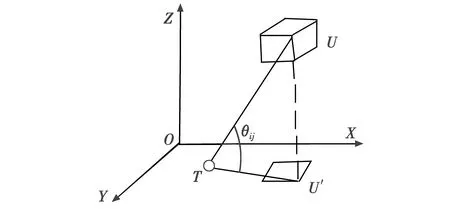
图1 空战态势图Fig.1 Air combat situation

2 多无人机协同任务分配模型的建立

以下两个方面的因素是进行多无人机任务分配时需要重点考虑的:1)在攻击敌方目标的过程中我方付出的代价，我方代价由被对方防空火力系统攻击所受到的毁伤代价和攻击目标时我方的燃油代价两部分组成；2)作战时对敌方目标的整体打击和毁伤效果。

2.1 目标价值收益指标函数

目标价值收益是指我方无人机攻击敌方目标对敌方目标造成的损耗。令无人机对目标的杀伤概率矩阵为P=[P1P2…Pm]，第i架无人机对目标的杀伤概率为

Pi=1-(1-ηi)ni

(5)

式中：ηi为第i架无人机对目标的单发命中概率，且无人机对目标打击是相互独立的事件；ni为第i架无人机携带的武器数。则第i架无人机攻击第j个目标时所产生的期望价值为

(6)

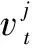
2.2 毁伤代价指标函数

(7)

(8)

式中：dij为无人机i与目标j的距离；e为敌方防空火力的有效射程；θ∈[0,1]是当敌方防空火力与无人机接触时摧毁无人机的效能。在作战过程中，无人机受到来自敌方防空火力的攻击,该无人机总的毁伤代价损失为

(9)

2.3 航程代价指标函数

无人机执行任务的航程代价与无人机执行任务期间飞行的路径有正相关的关系，则航程代价可表示为

(10)

式中：di为无人机i实际飞行的航程，即无人机i初始位置与打击位置之间的距离；dmax为所有无人机i中实际飞行的最大航程。

3 多无人机协同任务分配方法

已知无人机的初始位置和目标的位置后,就可将无人机在空中任意一点的能力量化,从而计算多无人机协同打击能力的决策位置和角度,计算各个方案总体目标收益函数,实现最优分配。

3.1 雅可比矩阵

雅可比矩阵可以将无人机的运动变化和能力函数联系起来，能力函数的雅可比矩阵可表示为

(11)

目标j获得的能力函数Bi相对于无人机i的坐标偏导数为

(12)

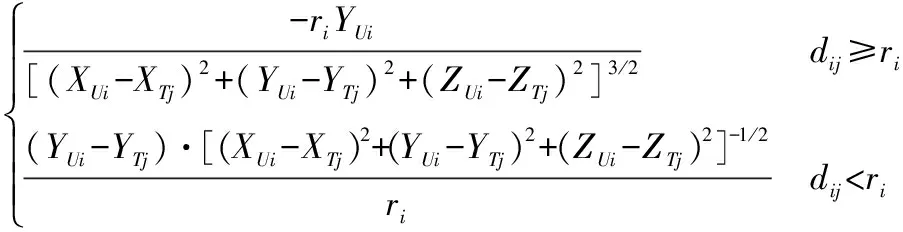
(13)

(14)

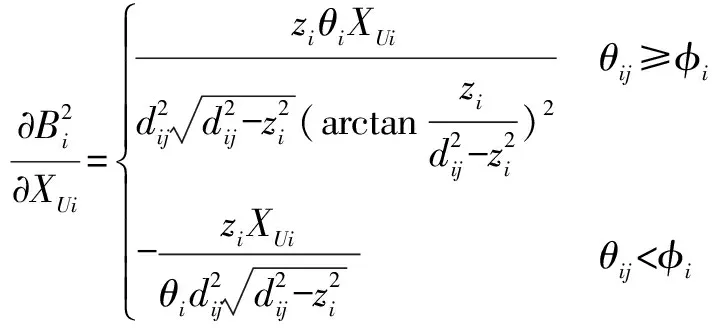
(15)

(16)

(17)

3.2 多无人机协同打击位置计算

能力函数由无人机的位置和角度决定，能力函数的变化与位置和角度的关系为

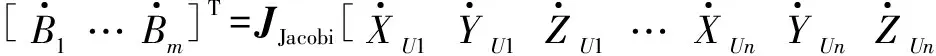
(18)

(19)

J+=JT(JJT)-1

(20)

(21)

3.3 多无人机协同打击位置与目标相对距离的计算

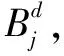
(22)

3.4 多无人机协同打击任务的总体收益模型

多无人机任务分配模型的总体目标函数可表示为

J=max(w1R-w2C1-w3C2)

(23)

s.t.

(24)

(25)

w1+w2+w3=1

(26)

式中：w1为价值收益指标；w2为毁伤代价权重；w3为航程代价指标权重。式(24)要求每架无人机每次最多分配给一个目标，式(25)要求最多h架无人机协同打击一个目标。

4 仿真验证

4架无人机攻击2个目标，有6种方案，如表1所示。

表1 分配方案Table 1 Allocation plan

表1中，方案1的分配矩阵为[1 2 3 4]，表示第1架和第2架无人机攻击目标1，第3架和第4架无人机攻击目标2。以下方案类似。

假设无人机的雷达扫描半径为4.5 km，不考虑导弹速度的前提下，当无人机与目标的位置距离为4.5 km，且无人机与目标的夹角φi为90°时，无人机具有最大的打击能力，在其他位置，距离越靠近4.5 km，夹角越靠近90°时，打击能力越大。

下面采用3种方法给出多无人机分配方案。

方法1通过式(21)更新无人机的位置，通过式(4)计算出多无人机协同打击位置能力值，然后分别通过式(6)、式(9)和式(10)计算目标价值收益、毁伤代价和航程代价，最后通过式(23)分别计算各个方案的收益值，最终得到各个方案收益值如表2所示。

表2 方法1的分配方案收益值Table 2 Revenue value of the allocation scheme of Method 1

通过表2可以看出，方案1的收益值最大，即第1架和第2架无人机攻击目标1，第3架和第4架无人机攻击目标2。目标1被打击的能力值见图2，目标2被打击的能力值见图3。

图2 目标1被打击的能力值Fig.2 The strike capability for Object 1

图3 目标2被打击的能力值Fig.3 The strike capability for Object 2

方法2通过式(21)更新无人机的角度，通过式(4)计算出多无人机协同打击角度能力值，然后分别通过式(6)、式(9)和式(10)计算目标价值收益、毁伤代价和航程代价，最后通过式(23)分别计算各个方案的收益值，最终得到各个方案收益值如表3所示。

表3 方法2的分配方案收益值Table 3 Revenue value of the allocation scheme of Method 2

通过表3可以看出，方案1的收益值最大，即第1架和第2架无人机攻击目标1，第3架和第4架无人机攻击目标2。

方法3以往多无人机任务分配方法[15]没有考虑多无人机打击位置能力函数，也没有考虑目标需要获得的能力值。按式(23)模型,得到各个方案收益值如表4所示。

表4 方法3的分配方案收益值Table 4 Revenue value of the allocation scheme of Method 3

第4种方案收益值最大，收益值为1.323 4，即第2架和第3架无人机攻击目标1，第1架和第4架无人机攻击目标2。

将表2、表3分别与表4对比可以看出:1) 方法1和方法2考虑了多无人机的协同打击能力函数；2) 方法1和方法3、方法2和方法3的决策结果完全不同；3) 方法1的收益和方法2的收益均比方法3的收益大，即方法1的最大收益为1.620 3，方法2的最大收益为1.682 0，而方法3的最大收益为1.323 4。因此,可以得出结论：在多无人机协同打击任务分配中，考虑能力函数与未考虑的分配方案相比，可获得更大的目标收益值，提高了多无人机协同打击能力。

5 结束语

通过建立无人机的能力函数及其雅可比矩阵，给出了多无人机协同打击位置和角度的计算方法，建立了多无人机协同打击任务分配模型，仿真结果表明：考虑多无人机协同打击能力的任务分配与未考虑的分配方案相比，可获得更大的目标收益值和毁伤效能，提高多无人机协同打击能力，是多无人机协同作战任务分配的一种技术探索尝试。

参考文献

[1] 付昭旺,寇英信,黄文卿,等.多机协同空战火力控制研究[J].电光与控制,2010,17(9):5-8.

[2] JOHNSON L B,PONDA S S,CHOI H L,et al.Asynchronous decentralized task allocation for dynamic environments[C]//Proceedings of the AIAA Infotech@Aerospace Conference,2011.doi:10.2514/6.2011-1441.

[3] 龙涛,沈林成,朱华勇,等.面向协同任务的多UCAV分布式任务分配与协调技术[J].自动化学报,2007,33(7):731-737.

[4] 刘毅,李为民,邢清华,等.基于双层规划的攻击无人机协同目标分配优化[J].系统工程与电子技术,2010,32(3):579-584.

[5] 魏铁涛,屈香菊.多机协同与多目标分配任务规划方法[J].北京航空航天大学学报,2009,35(8):917-920.

[6] 杜继永，张凤鸣,杨骥,等.多UCAV协同任务分配模型及粒子群算法求解[J].控制与决策，2012，27(11)：1751-1755.

[7] 陈侠,胡永新,徐光延.面向多无人机任务分配的二维编码粒子群算法[J].系统仿真学报,2013,25(12):3045-3049.

[8] O′ROURKE K P,CARLTON W B,BAILEY T G,et al.Dynamic routing of unmanned aerial vehicles using reactive tabu search[J].Military Operations Research,2001, 6(1):5-30.

[9] HARDER R W.A Java universal vehicle router in support of routing unmanned aerial vehicles air missions[D].Ohio:Air Force Institute of Technology,2000.

[10] NYGARD K E,CHANDLER P R,PACHTER M.Dyna-mic network flow optimization models for air vehicle resource allocation[C]//Proceedings of the American Control Conference,Arlington,Texas,2001：1853-1856.

[11]ALIGHANBARI M.Task assignment algorithms for teams of UAVs in dynamic environments[D].Cambridge：Massachusetts Institute of Technology,2004.

[12] 黎萍,杨宜民,练家乐.基于效用函数的多机器人系统任务分配[J].计算机应用研究,2009,26(2):537-539.

[13] 陈建平,苑召国,杨宜民.基于机器人效用函数的多机器人系统任务分配[J].计算机应用研究,2010,27(4):1339-1341.

[14] 李望西，黄长强，王勇.三维空间空战态势评估角度优势建模与仿真[J].电光与控制，2012,19(2):21-25.

[15] GIANLUCA A,STEFANO C,ALESSANDRO M.Decen-tralized deployment with obstacle avoidance for UAVs[C]//Proceedings of the 18th IFAC World Congress, Italy,2011:12807-12812．