基于GRACE的华北平原地下水储量时空变化分析
束秋妍, 潘 云, 宫辉力, 黄志勇, 郑龙群
(1.首都师范大学资源环境与旅游学院,北京 100048; 2.首都师范大学城市环境过程与数字模拟国家重点实验室培育基地,北京 100048)
0 引言
华北平原为我国第二大平原,也是我国的政治中心所在,人口稠密,是以旱作为主的农业区,拥有全国最大的小麦、玉米种植区,是全国重要的粮食基地。华北平原也是我国北方缺水较严重的地区,人均水资源量仅有450 m3,低于国际公认的极度缺水的标准(500 m3)[1]。地下水是区内主要供水源,随着工农业的生产发展及人口数量的不断增加,地下水的开采强度和开采规模不断增大。据统计,目前华北平原有地下水开采井约200万眼,从1985年到20世纪末,多年平均开采量已超过1010m3[2],且大部分用于农业灌溉。研究华北平原地区地下水储量变化的空间分布特征及时间变化规律,对于该区地下水资源可持续利用具有重要意义。
传统监测地下水储量变化一般利用监测井进行检测。这种实地测量地下水的方法仅依靠单点的地下水位,难以充分反映地下水储量在空间上和时间上的变化特征。GRACE(gravity recovery and climate experiment)重力卫星作为一种监测地表水储量变化的新型手段,打破了传统地面观测在时间和空间上的局限性,并已在国内外地下水水储量变化研究中得到了应用[3-5]。
经验正交函数(empirical orthogonal function,EOF)分析方法,通过分析矩阵数据中的结构特征,提取数据主要特征量,在水储量研究方面应用广泛。Awange等[6]利用EOF方法研究了埃塞俄比亚地区的陆地水储量、土壤湿度和降水的时空变化特征,并分析了三者的相关性及陆地水储量变化对降水的滞后性; Kang等[7]利用重力卫星数据结合EOF分析了中国2003—2010年间陆地水储量变化特征,发现水储量季节性变化与降水关系密切,其中梅雨季节和重大干旱时期在EOF分解的模态中都有体现; 阎福礼等[8]运用EOF方法分解了基于GRACE得到的长江流域水储量变化,较好地解释了该流域水储量变化的空间规律。
本文基于GRACE重力卫星反演华北平原地下水储量变化,并用实测数据加以验证。运用EOF对华北平原2003—2015年间地下水储量变化进行分解,分析地下水储量变化的时间和空间特征,并探讨控制其时空变化的主要因素。
1 研究区概况
华北平原位于我国东部,分布范围为E113.0°~ 119.5°,N34.5°~ 40.5°。北靠燕山,西傍太行山,南抵黄河下游,东临渤海,包括京津2市与河北省的全部平原区,以及山东、河南2省黄河以北的平原区,面积约为14万km2,总人口约1.33亿。华北平原地势较低,最高海拔为100 m左右,自北、西、南3个方向向渤海湾倾斜,海拔高度逐渐降低[9]。该区气候属中纬度大陆性半干旱季风气候,具有四季分明的特点,多年平均降水量约为550 mm,年内降水多集中在7—9月,占全年降水量的75%左右,冬季降水较少。华北平原有黄河、海河及滦河等大河流,此外还有徒骇河、马颊河及河北沿海诸河等直接入海的小河流,共有大小河流近60条。研究区位置如图1所示。

图1 研究区位置示意图
2 数据与方法
2.1 数据源
将德国地学研究中心发布的GRACE重力场模型产品减去一个平均重力场(或背景重力场),便可获取重力异常或时变部分。本文减去的是2005年1月至2010年12月平均重力场。所采用核函数格网分辨率为1°,经球谐展开并截断至60阶,去条带、高斯滤波处理(半径为200 km)后得到2003年1月—2015年8月期间152个月的陆地水储量变化(terrestrial water storage, TWS)数据,缺省月份的数据在实验处理的过程中一般取相邻数据的均值来替代。
由美国航空航天局戈达德空间飞行中心和美国海洋和大气局国家环境预报中心联合开发的全球陆面数据同化系统 (global land data assimilation system version1,GLDAS-1),可获取高精度、高空间分辨率的陆表水储量和能量信息。该系统驱动4个陆面过程模型: 通用陆面模型(common land model,CLM),Noah,Mosaic以及可变入渗能力模式(variable infiltration capacity,VIC)。本文采用2003年1月—2015年8月期间CLM模型的每月1°×1°土壤水储量(soil moisture storage,SMS)数据集。
从GRACE得到的TWS,包括地表水(湖泊、水库)、土壤水、地下水、雪水当量和植被冠层含水量等。反演地下水储量需考虑研究区域水文地质条件,扣除非地下水量。对于干旱半干旱区,土壤水储量是主要的非地下水部分。本文结合GRACE监测的总陆地水储量变化ΔTWS和水文模型得到的土壤水储量变化ΔSMS分离出地下水储量(ground water storage,GWS)变化,即
ΔGWS=ΔTWS-ΔSMS。
(1)
本文采用的实测地下水位数据来源于中国地质监测院编著的地下水位年鉴,共搜集了2005年1月—2013年12月期间年鉴中连续监测地下水位观测井数据,共64个; 采用的降水数据来自中国气象数据网(http: //data.cma.cn/),选取了2003年1月—2014年12月期间华北平原境内18个连续监测降水站点的观测数据。
2.2 EOF分析法
EOF分析也称经验正交函数分解,基本原理是对包含若干个空间点的变量随时间进行分解。设样本容量为m个点的资料,则空间中任意一点i和任一时间点j的变量值xij可看成由n个空间函数eofik和时间函数tkj(k=1 , 2 , … ,n)的线性组合[10]。将得到的GWS距平场以矩阵的形式表示如下
(2)
式中:m为空间点的个数,即空间网格点和测站等;n为时间样本数;X中第j列xj=(x1j,x2j,…,xmj)T即为第j个空间场。
然后计算矩阵X的协方差阵C,即
(3)
计算C的特征根(λ1,…,λm)和特征向量Vm×m,二者满足
Cm×mVm×m=Vm×mΛm×m,
(4)
式中Λ是m×m维对角阵,即

(5)
将特征值λ从大到小顺序排列,λ1>λ2>…>λm,每个非0的特征根对应一列特征向量值,也称eof。将特征向量投影到原始资料矩阵X上,就得到所有空间特征向量对应的时间系数(即主成分),表达式为
(6)
式中PC中每行数据就是对应每个特征向量的时间系数。
通常情况下,用前几个模态就可以近似地反映变量场的主要时空变化。模态的重要性可以用特征根的大小来判断,即特征根越大则其所对应的模态也越重要,同样表明对总方差的贡献率越高。第i个模态对整个变量场的贡献率P为

(7)
实际资料数据通过EOF分解后得到的空间模态是否是随机的,是否有物理意义,需要进行显著性检验[11]。在95%置信度水平下特征根的误差可通过式(8)得到检验,即

(8)
式中:Δλ为特征根误差;λ为各模态特征根;N*为自由度。当相邻的2个特征值满足λj=λj+1≥Δλ时,就认为这2个特征根可以分离,它们之间存在显著差别,其所对应的EOF才具有物理意义,否则将被排除。
3 结果与讨论
3.1 反演结果验证
计算华北平原内各个观测井从2005—2013年间的实测地下水数据均值,与GRACE计算得到的相应时段的GWS进行比较,检验数据精度。对比结果如图2和表1所示。

图2 GRACE反演和实测GWS变化时间序列

周年GWS均值2005年2006年2007年2008年2009年2010年2011年2012年2013年均值方差GRACE反演值126.5189.2136.288.1108.2106.2124.6172.5164.5135.133.7观测井实测值182.1148.6173.8111.1152.4142.0145.7150.7136.7149.220.5
从图2可以看出,2组数据的皮尔逊系数(pearson correlation coefficient)达到了0.754,说明实测地下水数据和计算得到的地下水数据具有较强相关性,表现在数据的周期和年度振幅变化一致性较好。表1中,GRACE反演得到地下水年度振幅均值为135.1 mm,方差为33.7,实测地下水周年振幅均值为 149.2 mm,方差为20.5。
3.2 GWS变化EOF分解
表2为华北平原GWS变化进行EOF分析后得出的前5个模态的方差贡献率。
表2华北平原地下水储量变化EOF分解后前5个模态累积方差贡献率
Tab.2Accumulatedvariancecontributionrateofthefirst5EOFmodelsofGWSinNorthChinaPlain(%)

参数EOF模态12345方差贡献率79.9311.764.661.680.81累计79.9391.6996.3598.0398.84
可以从表2中看出,模态1的方差贡献最大达到79.93%,远大于其他特征向量的方差贡献率,第2模态和第3模态方差贡献急剧收敛,分别为11.76%和4.66%,前3个模态的累积贡献率达到96.35%,基本可解释大部分变化特征,其余模态所占比重较小。而且当相邻的2个特征根过于接近时,EOF采样变异性会明显增大[12]。
在95%置信度水平下,按照式(5)计算特征根误差(图3)。从特征根误差范围看,第1—3模态特征根误差范围没有重叠,存在显著差别。而第4个特征根及以后的特征根误差范围基本上重叠,没有显著差别。综上考虑,本文仅选取前3个模态所对应的典型场,进一步分析华北平原GWS变化时空变化特征。

图3 华北平原地下水储量变化EOF分解特征根
3.3 GWS变化主要时空特征
前3个特征向量场及其分析如图4所示。

(a) GWS变化第1特征向量场 (b) 第一时间序列13点平滑值

(c) GWS变化第2特征向量场 (d) 第二时间序列13点平滑值
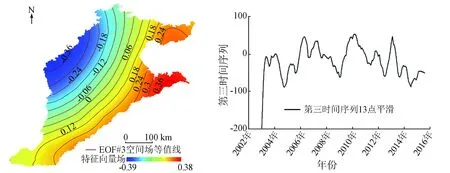
(e) GWS变化第3特征向量场 (f) 第三时间序列13点平滑值
图42003—2015年间华北平原GWS变化3个特征向量分析
Fig.4ThreefeaturevectorfieldsofvarietyofGWSfrom2003to2015inNorthChinaPlain
从图4中可以看出,第1特征向量场在华北平原内符号相同,表明华北平原地下水储量变化在空间变化上具有很好的一致性,表现为区域内地下水储量的增加或者减少,但南北地下水储量的变化幅度不同,南强北弱。这种全区一致的特性占总体方差的79.93%,说明影响华北平原地下水储量变化的因素比较单一,第1模态基本上表达了华北平原水储量变化场的主要结构。正值中心位于冀鲁豫3省交界区域,表明该区域的地下水变化幅度最大。从图4(b)可以看出,第1模态空间向量场对应的权重在逐渐减少,华北平原地下水呈现减少趋势。但这种多年的趋势性减少又表现出明显的年内季节性,即1—6月份表现为储量减少,而6—12月份表现为储量增加。这种趋势性减少、季节性变化与华北平原的地下水开采利用、降水量年内分布特征密切相关。由于长期过量超采[5],华北平原地下水储量在多年变化上表现为持续下降。这种下降主要是由于冬小麦的灌溉引起的[5]并导致了上半年地下水储量减少。在下半年,经过6—9月份的雨季补给,地下水储量又得到一定程度的恢复。从第1模态的方差贡献率看,这种自然-人为叠加的变化模式是华北平原GWS变化的主要特征,约占其总体变化的80%。第2特征向量场的方差贡献率为11.76%,表现为东北—西南格局,反映了沿海与内陆地下水变化呈现相反的趋势。正值中心在河南北部,0值线出现在研究区域中央,负值沿渤海湾分布。时间序列没有明显的趋势性变化,但年内波动大。这种时空变化可能与沿海-内陆的水文条件变化有关。第3特征向量场方差贡献率为4.66%,呈现出西北—东南相反的变化趋势。负值中心集中在太行山脉和燕山山脉的山前平原区,正值集中在渤海湾北部和南部地区。时间序列同样没有明显的趋势性特征。该模态可能受山前-平原的用水结构、水文地质条件影响,与Huang 等[13]研究结果相似,在山前地区地下水开采强度大,但补给量也大,地下水动态强烈。
4 结论
本文利用GRACE数据反演了华北平原2003年1月—2015年8月地下水储量变化,采用EOF方法对此进行时空分解,得到反映数据特征的前3个特征向量场,并对特征向量场和时间系数进行分析,得到如下结论:
1)华北平原地下水储量变化可以分解为3个主要模态,其对总体变化的解释率达到96.35%。
2)第1模态空间变化一致,表现出多年趋势性减少与年内季节性变化相结合的特征,可能由研究区内地下水开采、年内降水分布共同作用导致。这也是目前华北平原地下水储量减少的主要模式,对整体变化的解释率约为80%。
3)第2和第3模态分别表现出了东北—西南和西北—东南2种变化相反的空间格局,对总体变化的解释率分别约为12%和5%,在时间上没有明显的趋势性变化,推测可能主要受沿海-内陆、山前-平原的水循环和水文地质条件控制。
参考文献(References):
[1] 张利平,夏 军,胡志芳.中国水资源状况与水资源安全问题分析[J].长江流域资源与环境,2009,18(2):116-120.
Zhang L P,Xia J,Hu Z F.Situation and problem analysis of water resource security in China[J].Resources and Environment in the Yangtze Basin,2009,18(2):116-120.
[2] 刘昌明.建设节水型社会 缓解地下水危机[J].中国水利,2007(15):10-13.
Liu C M.Building water-saving society and alleviating groundwater crisis[J].China Water Resources,2007(15):10-13.
[3] Yeh P J F,Swenson S C,Famiglietti J S,et al.Remote sensing of groundwater storage changes in Illinois using the gravity recovery and climate experiment (GRACE)[J].Water Resources Research,2006,42(12)W 12203:1-7.doi:10.1029/2006WR005374.
[4] Feng W,Zhong M,Lemoine J M,et al.Evaluation of groundwater depletion in North China using the gravity recovery and climate experiment (GRACE) data and ground-based measurements[J].Water Resources Research,2013,49(4):2110-2118.
[5] 张光辉,费宇红,刘春华,等.华北平原灌溉用水强度与地下水承载力适应性状况[J].农业工程学报,2013,29(1):1-10.
Zhang G H,Fei Y H,Liu C H,et al.Adaptation between irrigation intensity and groundwater carrying capacity in North China Plain[J].Transactions of the Chinese Society of Agricultural Engineering,2013,29(1):1-10.
[6] Awange J L,Gebremichael M,Forootan E,et al.Characterization of Ethiopian mega hydrogeological regimes using GRACE,TRMM and GLDAS datasets[J].Advances in Water Resources,2014,74:64-78.
[7] Kang K X,Li H,Peng P,et al.Low-frequency variability of terrestrial water budget in China using GRACE satellite measurements from 2003 to 2010[J].Geodesy and Geodynamics,2015,6(6):444-452.
[8] 阎福礼,李书明,王世新,等.基于EOF方法长江流域2002—2013年GRACE水储量时空变化研究[J].长江流域资源与环境,2015,24(S1):131-137.
Yan F L,Li S M,Wang S X,et al.Temporal and spatial variations research of GRACE water storage changes over the Yangtze River Bisin[J].Resources and Environment in the Yangtze Basin,2015,24(S1):131-137.
[9] 张兆吉,雒国中,王 昭,等.华北平原地下水资源可持续利用研究[J].资源科学,2009,31(3):355-360.
Zhang Z J,Luo G Z,Wang Z,et al.Study on sustainable utilization of groundwater in North China Plain[J].Resources Science,2009,31(3):355-360.
[10] 魏凤英.全国夏季降水区域动态权重集成预报试验[J].应用气象学报,1999,10(4):402-409.
Wei F Y.Regional consensus forecast method with dynamic weighting for summer precipitation over China[J].Quarterly Journal of Applied Meteorlolgy,1999,10(4):402-409.
[11] 施 能,章爱国,余锦华.气象学中使用统计检验的几个重要注记[J].气象科学,2009,29(5):670-673.
Shi N,Zhang A G,Yu J H,Some important problems of the statistics test in meteorology[J].Scientia Meteorologica Sinica,2009,29(5):670-673.
[12] North G R,Bell T L,Cahalan R F,et al.Sampling errors in the estimation of empirical orthogonal functions[J].Monthly Weather Review,1982,110(7):699-699.
[13] Huang Z Y,Pan Y,Gong H L,et al.Subregional-scale groundwater depletion detected by GRACE for both shallow and deep aquifers in North China Plain[J].Geophysical Research Letters,2015,42(6):1791-1799.

