考虑交货因素的热轧无缝钢管订单排程模型与算法
吴子轩,李铁克,张文新,王柏琳,王建建
(1.北京科技大学东凌经济管理学院,北京 100083;2.钢铁生产制造执行系统技术教育部工程研究中心,北京 100083)
1 引言
无缝钢管作为一种重要的工业生产资料,广泛用于国民经济的各个生产领域,企业通常按照外径、壁厚、钢种、长度等参数将钢管划分成不同的规格,将满足一定条件的订单按规格统一组织,实现批量化生产。一套完整的现代热轧无缝钢管生产要经过钢坯加热、穿孔、连轧、张减定径和精整、热处理等多道工序,跨越数个作业区。其中连轧工序是无缝钢管生产的重中之重。热轧轧制订单计划决定了整条产线的生产节奏和前后工序的工艺调整,并直接影响到订单交付和成品物流配送。
目前关于热轧无缝钢管订单排程问题的研究并不多见,与之相关的研究有:王海凤等[1]在假设组批完成的前提下,以生产跳跃惩罚最小为目标给出热轧无缝钢管生产排序问题的约束满足模型;Tang Lixin和Huang Lin[2]认为热轧无缝钢管的生产具有以下四个特点:批量可调度性、生产多阶段性、品种规格的多样性且机器调整时间因批量规格而异;李建祥等[3]总结出7条关于钢管组批和排序的规则,对钢管的生产计划和调度的研究具有借鉴意义;Li Lin等[4]研究了宝山无缝钢管厂冷区生产调度问题,针对现实生产约束提出了混合流水车间调度问题的混合整数非线性规划模型;Jia Shujin等[5]将热轧批量调度问题归结为基于奖金收集车辆路径问题并提出多目标优化模型;许绍云等[6]以最大化产能利用率、最小化机器调整时间和订单提前拖期为优化目标,建立针对圆钢热轧批量调度问题的多目标整数规划模型;Jia Shujin等[7]将热轧批量调度问题归结为一个带双时间窗的车辆路径问题的多目标模型。热轧订单排程问题属于NP难的组合优化问题,目前多采用智能优化算法和聚类算法相结合的方式求解。其中,王海凤等[1]设计了节点互换算法解决无缝钢管生产计划中的生产排序问题;Jia Shujin等[5]使用基于分解策略和帕累托最优的蚁群算法对模型进行求解;许绍云等[6]提出一种改进的带精英策略的快速非支配排序算法对批量调度模型进行求解;张文学和李铁克[8]针对面向复杂生产工艺的三阶段一体化批量计划模型(无优化目标),考虑到问题的NP难特点,提出了将约束传播技术嵌入到聚类分析中的求解算法。
上述研究提供了良好的基础,但在以下方面尚需进一步研究:在研究对象方面,首先,已有研究大多关注订单的生产因素,如产品规格、生产工艺等,对交货因素等其他属性则考虑甚少。而在目前的市场环境下,订单交付能力日渐成为钢铁企业一项核心竞争力,相近交货日期和地址的订单集中生产能提高运输效率,订单交货期的满足能提高客户满意度。因此有必要在订单排程中考虑交货因素;其次,热轧订单排程是源于现实中的生产管理问题,但据作者所知已有研究多单独研究组批或排序问题,未有建立集成模型对订单排程问题展开研究的。在求解算法方面,热轧订单排程问题是NP难的,难以使用精确算法求得最优解。我们在算法设计过程中发现:由于钢铁产品具有严苛的生产工艺要求,一般智能优化方法既难以有效构建合适的初始解,也易在计算中产生不可行解或陷入局部最优,传统智能优化算法如何更好应用于工程优化问题尚需进一步研究[9]。因此需要根据问题特征来设计和改进优化算法。基于上述分析,本文将研究考虑订单交货期、配送地址等交货因素的热轧无缝钢管订单排程问题,设计集成订单组批和批量排序的订单排程数学模型,进而针对模型特征设计基于聚类和混合变邻域搜索的两阶段求解算法。
2 问题建模
2.1 问题描述
在企业与客户签订供货合同后,生产部门将销售合同分解为生产订单并进行订单排程,而后将订单排程计划下发给生产车间和原料厂,原料厂根据排程计划供应钢坯。生产订单是企业对销售合同的分解和再处理,便于合同排产,因此同一生产订单内的产品具有相同的工艺属性要求。热轧订单排程是在销售合同分解为生产订单(以下统称为“订单”)后,将一段时间内一定数量的订单按照轧制规格(外径、钢种、壁厚、长度等)工艺属性和交货时间、交货地址等交货属性进行订单组批,形成热轧批次(以下简称为“轧批”),再将轧批排定生产次序的过程。订单排程的最终结果是一系列有序的轧批,每个轧批具有相同的工艺属性和相似的交货属性。一个轧批可以包含单个或多个订单,每个订单只能属于一个轧批。排程过程中要充分考虑生产和交货中的成本因素,避免因为切换规格导致频繁的机器设备调整,避免过多的中间库存和成品库存堆积。此外,不同于以往研究,本文重点考虑了合同的交货期和交货地址,使具有相似交货属性的订单尽量集中生产并交付。
2.2 模型假设
对于考虑合同交货的热轧无缝钢管订单排程优化问题,根据生产实际提出如下合理假设:
(1)仅考虑由轧制规格变化所引发的机器设备调整,且不同规格切换引发的调整时间相同,不考虑设备突发故障和现场突发事故等动态情况;
(2)在生产过程中,机器设备的调整成本与相邻批次外径差和钢种差的绝对值成正比,其中,外径差和钢种差是按照工厂对外径、钢种差异的界定转化为数字表示;
(3)忽略不同订单的备存成本差异,库存成本由订单的提前生产产生;
(4)本文问题考虑的是生产订单,即合同订单按产品和产量分解后用于指导生产的订单,同一订单内的产品具有相同属性。
2.3 符号定义
为了便于模型的描述和建立,给出符号和变量如下:
(1)索引与集合
I为所有计划轧制批编号的集合,I={1,2,…,n};i为轧制批次编号,i∈I;
J为订单的集合J={1,2,…,m},其中m为订单总数;j为订单编号,j∈J;
Li为轧制批次i所包含的订单有序集合,Li(v)表示轧批i内的第v个订单;轧制计划集合为{L1,L2…Ln}。
(2)符号定义
Pd为相邻批次外径变化造成机器调整的惩罚参数,Pd∈[0,1];
Psg为相邻批次钢种变化造成机器调整的惩罚参数,Psg∈[0,1];
Pte,Ptl分别为订单提前和订单拖期的单位时间惩罚参数,Pte,Ptl∈[0,1];
dj,wj,sgj,lj分别为订单j的轧制外径、壁厚、钢种和长度;
[dsj,dej]为订单j的交货期窗口;
(aj,bj)为订单j的配送地坐标;
ptj为为订单j的计划轧制时长;
qtyj为为完成订单j所需要轧制的管坯数量;
deti为轧批i的最晚交货期,根据该轧批所包含订单集合的最晚交货期求得;
zmax为单个批次所允许的最大轧制数量;
A为足够大的正整数。
(3)决策变量
sti,eti分别为轧批i的开工时间和完工时间;
2.4 数学模型
针对热轧无缝钢管订单排程问题,建立以机器设备调整、提前/拖期和配送地域差异度最小为目标的数学模型,具体如下:
minF1=
(1)
(2)
(3)
s.t.
|dj-dj′|·xij·xij′=0,j,j′∈J,i∈I
(4)
|wj-wj′|·xij·xij'=0,j,j′∈J,i∈I
(5)
|sgj-sgj′|·xij·xij′=0,j,j′∈J,i∈I
(6)
|lj-lj′|·xij·xij′=0,j,j′∈J,i∈I
(7)
(8)
(9)
xij·xi′j=0,j∈J,i≠i′,i,i′∈I
(10)
(11)
(12)
(13)
(sti′-eti)·yii′≥0,i,i′∈I
(14)
sti,eti≥0,i∈I
(15)
xij,yii′∈{0,1},i∈I,j∈J
(16)
目标函数(1)表示在组批过程中最小化每个批次内所包含订单配送中心地理位置的差异。目标函数(2)表示最小化轧批间轧制规格(外径、钢种)切换所导致的机器设备调整的频率;目标函数(3)表示最小化提前和拖期生产惩罚使订单能够适期生产,针对提前生产或拖期的惩罚值各不相同。
约束(4)~(12)与组批相关,其中,约束(4)表示同一批次内的订单外径相同;约束(5)表示同一批次内的订单壁厚相同;约束(6)表示同一批次内的订单钢种相同;约束(7)表示同一批次内的订单长度相同;约束(8)表示受钢坯生产供应、生产管理因素和轧机、轧辊、定径机可用的最大生产能力的影响,一个批次内的轧制数不超过预先设定的最大值,这也间接约束了可排入同批生产的订单;约束(9)表示一个批次至少包含一个订单;约束(10)表示一个订单只能匹配给一个批次;约束(11)表示轧批的最晚交货期,根据该轧批所包含订单集合的最晚交货期求得;约束(12)表示所有订单都参与组批。
约束(13)~(15)与排序相关,其中,约束(13)表示轧批在轧制时不允许中断;约束(14)表示前一个轧批轧制完成后下一个轧批才能开始轧制;约束(15)表示开始和结束时间非负。
约束(16)为整数变量的取值约束。
3 求解算法
本文的热轧无缝钢管订单排程模型是一类多目标、多约束的混合整数规划模型,且在实际生产中,由于生产连续性的要求,同期生产的订单规模往往较大,难以采用精确算法在有限时间内取得问题的解。为了提高求解效率及解的有效性,本文结合无缝钢管成批量的生产特征,设计了一种两阶段混合优化算法。第一阶段基于带凝聚策略的层次聚类思想设计了一种订单聚类算法,进行订单组批并形成初始轧制计划,第二阶段使用嵌入模拟退火思想的变邻域搜索算法对初始批次进行排程优化。
3.1 初始排程
本阶段首先对订单进行组合,并形成初始轧制批次,在此过程中遵循以下两类原则:①工艺属性相同性原则;②交货属性相似性原则。工艺属性相同性是指同一批次内的订单必须具有相同的规格以满足热轧钢管轧制工艺规范要求,这也符合成组技术[10]的思想,实现集中生产以降低成本。交货属性相似性是指同一轧批内不同订单交货时间和配送地址允许具有一定相近性,而不要求完全相同。层次聚类是聚类分析的一个分支,它是一种用于形成群体或集群的系统性方法,具有高计算性的特点,通过按照某种策略对数据集进行层次分解,直至条件得到满足[11]。目前层次聚类方法已经广泛应用于解决与生产制造和供应链物流配送相关的问题[12]。本文改进了层次聚类算法,通过在订单预处理阶段考虑工艺约束,并在聚类中心和相对距离的计算中融入了订单的交货时间和交货地址,设计了一种订单聚类算法(Order clustering algorithm, OCA)来满足交货属性相似性要求。
3.1.1 订单预处理
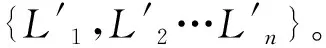
3.1.2 基于聚类的初始轧批生成
通过预处理得到的粗批次满足了约束(4)~(7),需要进一步优化以实现订单初始排程,最小化批次内订单的差异性,实现交货属性相似性的要求。根据分类原理的不同,层次聚类可以分为凝聚和分裂两种策略[13]。本文需要将每个粗批次内分散的订单进行聚类形成初始轧批,因此根据问题特征选用凝聚策略。
此外,若在订单组批阶段就考虑交货期相似性,能够为排序优化阶段提供良好的初始解,提高目标函数(3)的优化效率和效果。为此,在这里提出最小化批次内订单交货期的差异值的优化目标,作为目标函数(3)的辅助目标,见式(17)。式(1)和(17)是衡量订单间的相似程度进而设计订单间距离公式的重要依据。
(17)
在带凝聚策略的层次聚类算法中,初始聚类中心的选择会对聚类结果产生重要影响。本文通过在每个粗批次内计算订单间相对距离以表示订单相似度的方法,取最小相对距离为初始聚类中心(新类),并不断将与初始聚类中心相对距离最小的订单加入该类中直至达到单批产能限制为止,计算新聚类中心。
为计算订单间的相对距离并得到聚类中心,可以将订单数值化描述为:j(otj,odj),其中otj为订单j的交货期窗口[dsj,dej];odj(aj,bj)为订单j交货地址的坐标,即成品配送的地理位置。对于Li′内的两个不同订单j,j′,我们设计了公式(18)来计算两订单间的相对距离,其中(dsj+dej)/2-(dsj′+dej′)/2反映了订单间交货期的相对差异,(aj-aj′)2+(bj-bj′)2反映了订单间配送位置的相对差异。
(18)
对于聚类中心,算法采用一个类中所有订单间相对距离的算术平均值来表示,该值在聚类过程中是不断变化的,计算公式见式(19),其中r为当前聚类中心所包含订单的总数。
avg(ot,od)=([∑ds/r,∑de/r], (∑a/r,∑b/r))
(19)
3.1.3 初始排程的算法步骤
形成初始批次{L1,L2…Ln}的算法步骤如下:
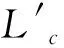
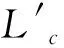
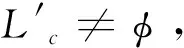
步骤6 终止条件判断
该新类作为初始批次Li,输出初始批次集合{L1,L2…Ln};若L'c≠φ,则令i←i+1,执行步骤2;若c 基于OCA得到的订单排程是问题的一个可行解,但在最小化机器调整时间和适期交货方面还需要进一步优化。若将每个初始轧批视为工件,将热轧过程视为处理机,本阶段问题可抽象为一类考虑交货期和机器调整的单机调度问题。Arroyo等[14]证明了在最小化提前/拖期和序列相关机器设置时间的单机调度问题中应用变邻域搜索算法是可行的。变邻域搜索(Variable Neighborhood Search, VNS)属于单点元启发式算法[15],VNS的创新之处主要包括动态变化的邻域结构和局部搜索,通过在搜索过程中系统地改变邻域结构集以拓展搜索范围,达到局部最优解不断地向全局最优解收敛的目的[15],该算法所具有的灵活性决定其可根据实际问题设计各种变形,并结合其他算法使用,以提高搜索性能[17-18]。Xiao Yiyong等[17]将变邻域搜索算法与模拟退火算法结合,模拟退火算法(Simulated Annealing, SA)是解NP难组合优化问题的有效近似算法,该算法能够克服传统优化算法易陷入局部极值的缺点[20-21]。嵌入模拟退火思想的变邻域搜索算法既秉承了变邻域搜索算法进行大范围变邻域搜索的优点,又利用模拟退火思想避免算法陷入局部最优,两者的结合可以有效提高算法的搜索效率和解的质量[17-19]。 基于上述分析,本阶段借鉴Hansen和Mladenovic[16]中基本变邻域搜索算法(basic Variable Neighborhood Search, bVNS)的算法框架和Xiao Yiyong等[17]将模拟退火思想嵌入变邻域搜索算法的设计思路,提出了混合变邻域搜索算法(Hybrid variable neighborhood search, HVNS),对得到的初始批次排程做进一步优化。在HVNS中,我们根据本文问题特征和应用背景设计了一种解的接受准则,并确定了搜索算子。算法的详细设计及步骤如下。 3.2.1 算法初始化 算法初始化是对以下3类信息进行明确的过程:①根据问题特征和模拟退火思想设置算法运行所需的参数;②确定初始轧制批次集合{L1,L2…Ln}及其对应的初始解SEQ0;③将模型中的F2和F3设定为轧批排序的优化目标,并计算初始解的目标函数值。 3.2.2 邻域结构 构造邻域结构是变邻域搜索算法的核心内容,通过变换邻域结构以对更广阔的空间进行搜索。考虑到本文的解为一个置换序列,算法采用交换(Swap)算子和插入(Insertion)算子构造邻域结构集合,Swap算子是从当前解中随机选取两个相异节点,交换两点位置形成新的邻域结构,将所有可能邻域结构组成的集合称为当前邻域的交换式邻域。Insertion算子是从当前解中随机选择一个节点,并将其插入其他位置形成新的解,把所有可能形成的新解构成当前解关于该节点的插入式邻域。已有研究已证明了上述两种算子对于生成置换序列邻域的有效性[14, 18]。 3.2.3 局部搜索 局部搜索是对每次生成的邻域结构进行局部搜索,得到该邻域结构中的局部最优解,通过解的接受准则决定是否使用当前解更新局部最优解。局部搜索既是邻域搜索的重要组成部分,也是最消耗计算资源的部分,必须针对问题特点制定搜索策略。本文采用or-opt算子进行局部搜索,将当前解中顺序相连的部分节点移动到解路径上的另一个位置上,得到新的局部解。 3.2.4 解的接受准则 解的接受准则主要包括局部最优解更新和全局最优解更新这两个方面。 针对多目标问题中局部最优解的更新问题,本文采用在多目标串行优化中嵌入模拟退火算法解的接受准则的决策方式。针对当前钢铁企业的普遍情况,本文为生产因素赋以比交货因素更高的影响因子,遵循以下规则进行更新: 规则1:若目标函数F2的值得到优化,或F3相同且F2的值得到优化,即可更新局部最优解。 规则2:若F2得到优化但F3值变差,则执行模拟退火算法中解的接受准则决定是否更新,接受准则见式(20),其中r0为位于0-1区间的随机数。 (20) 规则3:其他情况均保留原解。 关于全局最优解的接受与更新,考虑到生产因素的重要性,当局部最优解的F3不小于当前值且局部最优解的F2小于当前值时,可以更新全局最优解。 3.2.5 终止条件 基于模拟退火的思想,在当前温度小于终止温度时,终止搜索并输出计算结果。 3.2.6 算法步骤 步骤1算法初始化 步骤1.1从数据库获取初始轧制批次集合{L1,L2…Ln},其轧制序列既是初始解SEQ0; 步骤1.2设定局部最大搜索次数MaxSearch、当前搜索次数k=0,模拟退火中的初始温度T0、终止温度Tf、降温系数α、降温迭代次数nT、降温函数Tk+1=αTk; 步骤1.3令全局最优解为SEQb←SEQ0,对应的全局最优目标函数值为FB2(SEQb)和FB3(SEQb); 步骤2邻域构造 步骤2.1采用插入算子(Insertion)或交换算子(Swap)构造关于当前轧制批次集合的邻域结构集合NBK(K=1,2),kmax=2,K=1; 步骤2.2令k←k+1、nT=0、当前温度为Tk=αTk-1,随机从NBK中生成解SEQNBK,令当前局部最优解SEQ←SEQNBK,计算目标函数值F2(SEQ)和F3(SEQ); 步骤3局部搜索 步骤3.1令nT←nT+1,针对SEQNBK执行or-opt的局部搜索操作,得到当前局部解SEQt; 步骤3.2计算当前局部解SEQt的目标函数值F2(SEQt)和F3(SEQt); 步骤3.3若F2(SEQt) 步骤3.4生成随机数r0∈[0,1],若满足模拟退火接受准则(式(20))则令SEQ←SEQt更新局部最优解,转到步骤3.5; 步骤3.5若nT=MaxSearch终止局部搜索,否则重新执行步骤3.1; 步骤4更新历史解 若F2(SEQ) 步骤5判断终止条件 步骤5.1若Tk 步骤5.2排程寻优停止,全局最优解SEQb作为最终解,并输出以全局最优解排列的最终订单排程结果{L1,L2…Ln}。 为检验模型和算法在现实生产中的可行性和有效性,本文采用某典型国有大型钢厂的实际订单数据进行实验设计,共采集8组由300个订单的整数倍组成的样本。此样本数据的工艺和交货相关参数均采用行业通用标准,订单规模覆盖了大中小型热轧无缝钢厂可能的产能范围,适用于国内各钢铁企业。订单按模型参数要求进行整理后输入模型中。 订单样本包含的属性有:订单编号、轧制外径、轧制钢种、轧制壁厚、轧制长度、计划轧制支数、计划轧制时长、交货期窗口时间和配送地址坐标。根据该钢厂现实生产状况,将模型中目标函数惩罚值Pd、Psg、Pte、Ptl分别设置为0.6、0.4、0.2、0.8,zmax=2000,et=15min。关于对比算法的设计,考虑到本文研究问题的独特性和复杂性,以及无缝钢管生产工艺约束限制,已有算法不能直接应用到本文问题。因此,本文将实验分为两阶段,并分别设置如下对比算法:在第一阶段实验中,将订单分组算法(Order grouping algorithm, OGA)和本文提出的OCA进行对比,生成初始排程,通过目标函数F1和F4衡量二者所生产初始排程的优劣。OGA是一种不考虑交货因素的分组算法,参考了文献[1~3]中针对工艺属性相同性进行组批的传统方法,并针对本文订单排程模型的约束进行了分组设定。第二阶段实验在由OGA和OCA分别生成的初始排程基础上,对比bVNS和本文设计的HVNS的排程寻优性能,其中bVNS不使用模拟退火思想控制计算的总迭代和解的接受准则。考虑到初始排程方法和排程优化方法的优化重点不同,第一阶段实验的衡量指标为F1-F4这4个目标函数;第二阶段实验则重点考察目标函数F2和F3;另外,两组实验都将给出计算时间,以衡量算法的效率。 上述算法均使用Visual C#编写,编译于Microsoft .Net Framework 3.5软件环境下,并运行在Intel i7-3840QM 3.8GHZ CPU/16.00GB的硬件环境下。 表4-1和表4-2给出了两阶段实验的结果。其中,F1、F2、F3、F4分别表示模型的四个目标函数值,CPU Time表示算法的计算时间。 表4-1 订单初始排程实验结果 由表4-1可以看出,对于初始排程生成算法,在每种订单规模下,OCA得到的初始排程结果(F1、F4)都优于OGA,且相对优势为4%~13%。面对实验中八组不同规模的订单样本,两种算法的耗时均在1.25s以内。这说明两种算法都能将订单有效组织成轧批,而OCA通过订单间的相对距离计算体现订单分布的聚类中心,再根据聚类中心进行订单聚集,这种思想能够有效将交货地址和交货时间相近的订单聚合成轧批集中生产,因此其F1和F4的目标值明显优于OGA。在实现两种算法时应用了.Net成熟的分组函数,这使得计算耗时较少,而OCA比OGA消耗更多时间,主要是因为OCA需要根据式(18)和(19)不断计算订单间差异并生成聚类中心,这是项耗时的工作。 表4-2 订单优化排程实验结果 由表4-2可以得到,对于排程优化算法,在每种订单规模下,经过排程优化后得到的F2和F3都要比初始排程后的结果有所改善。这是因为初始排程阶段重点解决订单组批问题,其形成的订单排程结果能够满足工艺属性相同性和交货属性相似性要求,但轧批间的排序需要进一步优化。由HVNS得到的排程结果优于bVNS,这是因为HVNS在局部搜索中引入了模拟退火算法的思想,通过容忍一定概率的劣解防止搜索陷入局部最优,搜索域相对更宽阔。而bVNS仅通过随机的邻域变化寻找最优解(F2、F3),容易陷入局部最优,影响全局优化效果。 此外,基于OCA的初始排程寻优得到的最终结果要优于OGA,主要原因如下:首先,在基于OGA的初始排程中,同批次的订单在交货属性(特别是交货期)上具有较大差距,而OCA则通过聚类保证了同批次订单交货期和交货地址的相似性。其次,生产订单是由销售合同分解的,部分面向大工程的合同对某些规格有集中需求,且部分地域的客户在规格需求上也往往具有一定相似性,这使得相似订单在初始阶段被聚类在同个或相邻批次中,这为后续排程优化也打下良好基础。同时进一步验证了OCA算法的有效性。 从表4-2给出的计算时间来看,HVNS的计算时间比bVNS要长。这主要是由于HVNS算法引入模拟退火思想,HVNS的运算规模大于bVNS,当订单规模增加,其搜索范围和计算量将相应增加。但本实验的最大订单规模达到2400,相当于一般大型钢厂的中长期订单排程需求,在此规模上HVNS于6min内获得了排程结果,完全能够满足实际的计划需求。而由此能够取得F2相较于bVNS的30%到45%的优化,同时F3也能得到1%到6%的优化,降低了由机器调整和提前/拖期生产造成的成本。因此,对于HVNS而言,其在计算时间与优化效果上的平衡是值得的。 综上所述,实验通过八组不同订单规模的样本,测试了模型及OCA和HVNS在订单排程中的可行性和有效性,该组合算法在合理的时间范围内可以得到相对更优的排程结果。 热轧订单排程是无缝钢管生产管理中的重要问题,目前大多数研究主要基于产品规格,很少涉及订单交货和配送等因素。本文在充分考虑了无缝钢管的生产工艺要求和产品特点的基础上,综合考虑订单交货期和交货地址,以订单适期交货、集中生产和配送、机器设备调整频率最小为目标设计了问题的混合整数规划模型。在模型的求解方面,本文基于过往研究并结合冶金行业的生产特征和本文研究问题的特点,首先基于带凝聚策略的层次聚类算法思想,按工艺属性相同和交货属性相似的要求,定义了订单间的距离公式,设计了一种订单聚类算法进行订单组批并形成初始轧制计划。然后通过构造符合本文问题特征的解的接受准则和搜索算子,设计了混合变邻域搜索算法对初始批次进行排程优化。基于实际订单数据的仿真实验验证了模型和算法的可行性和有效性。实验结果表明,该模型在满足热轧无缝钢管生产特点的同时,优化了合同对于交货与配送的需求,且本文提出的算法能够在各订单规模上得到相对优化的订单排程结果,能够对热轧无缝钢管的生产管理起到指导作用。 参考文献: [1] 王海凤,薛美美,李铁克.基于约束满足的热轧无缝钢管生产排序模型与算法[J].冶金自动化,2013,37(3):39-42. [2] Tang Lixin, Huang Lin. Optimal and near-optimal algorithms to rolling batch scheduling for seamless steel tube production[J]. International Journal of Production Economics,2007,105(2):357-371. [3] 李建祥,唐立新,吴会江,等.基于规则的热轧钢管调度[J].钢铁,2004,39(9):39-42. [4] Li Lin, Huo Jiazhen, Tang Ou. A hybrid flowshop scheduling problem for a cold treating process in seamless steel tube production[J].International Journal of Production Research, 2011, 49(15):4679-4700. [5] Jia Shujin,Yi Jian,Yang Genke,et al. A multi-objective optimisation algorithm for the hot rolling batch scheduling problem[J].International Journal of Production Research,2013,51(3):667-681. [6] 许绍云,李铁克,王雷,等.考虑机器检修的圆钢热轧批量调度算法[J].计算机集成制造系统, 2014, 20(10): 2502-2511. [7] Jia Shujin, Zhu Jun, Yang Genke,et al. A decomposition-based hierarchical optimization algorithm for hot rolling batch scheduling problem [J]. The International Journal of Advanced Manufacturing Technology, 2012, 61(5): 487-501. [8] 张文学,李铁克.面向多种生产工艺的冶铸轧一体化批量计划优化[J].计算机集成制造系统,2013,19(6):1296-1303. [9] 薛羽.仿生智能优化算法及其应用研究[D].南京: 南京航空航天大学,2013. [10] Pan Changchun, Yang Genke. A method of solving a large-scale rolling batch scheduling problem in steel production using a variant of column generation[J]. Computers & Industrial Engineering, 2009, 56(1):165-178.. [11] Everitt B, Landau S, Leese M, et al. Cluster analysis, Wiley series in probabilityand statistics[M]. Chichester, UK: Wiley; 2011. [12] Daie P, Li S. Hierarchical clustering for structuring supply chain network in case of product variety[J]. Journal of Manufacturing Systems, 2016, 38:77-86. [13] 段明秀.层次聚类算法的研究及应用[D].长沙:中南大学,2009. [14] Arroyo J E C, Rafael D S O, Alcione D P O. Multi-objective variable neighborhood search algorithms for a single machine scheduling problem with distinct due windows[J]. Electronic Notes in Theoretical Computer Science, 2011, 281(1):5-19. [15] Mladenovic N, Hansen P. Variable neighborhood search[J]. Computers & Operations Research, 1997, 24(11):1097-1100. [16] Hansen P, Mladenovic N. Variable neighborhood search:Principles and applications[J]. European Journal of Operational Research, 2001, 130(3):449-467. [17] Xiao Yiyong, Zhao Qiuhong, Kaku I, et al.Variable neighbourhood simulated annealing algorithm for capacitated vehicle routing problems[J].Engineering Optimization, 2014, 46(4):562-579. [18] 柏亮,李铁克,王柏琳,等.基于变邻域搜索的热轧圆钢批量调度多目标优化方法[J].工程科学学报,2015,37(1):111-117. [19] 王雷,许绍云,赵扬,等.有限缓冲区的多节点订单接受模型与算法[J].中国管理科学,2015,23(12):135-141. [20] Yu V F, Lin S Y. A simulated annealing heuristic for the open location-routing problem[J]. Computers and Operations Research, 2015,62:184-196. [21] Bandyopadhyay S, Saha S, Maulik U, et al. A Simulated annealing-based multiobjective optimization algorithm:AMOSA[J]. IEEE transactions on evolutionary computation, 2008, 12(3):269-283.3.2 排程优化
4 数据实验与分析
4.1 实验环境与数据
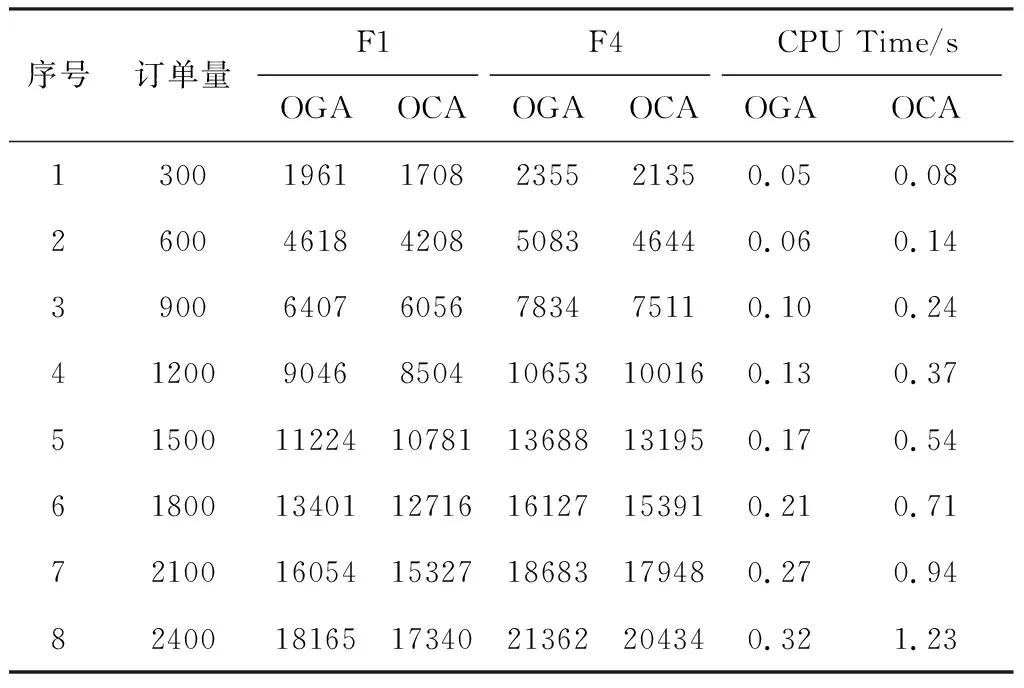
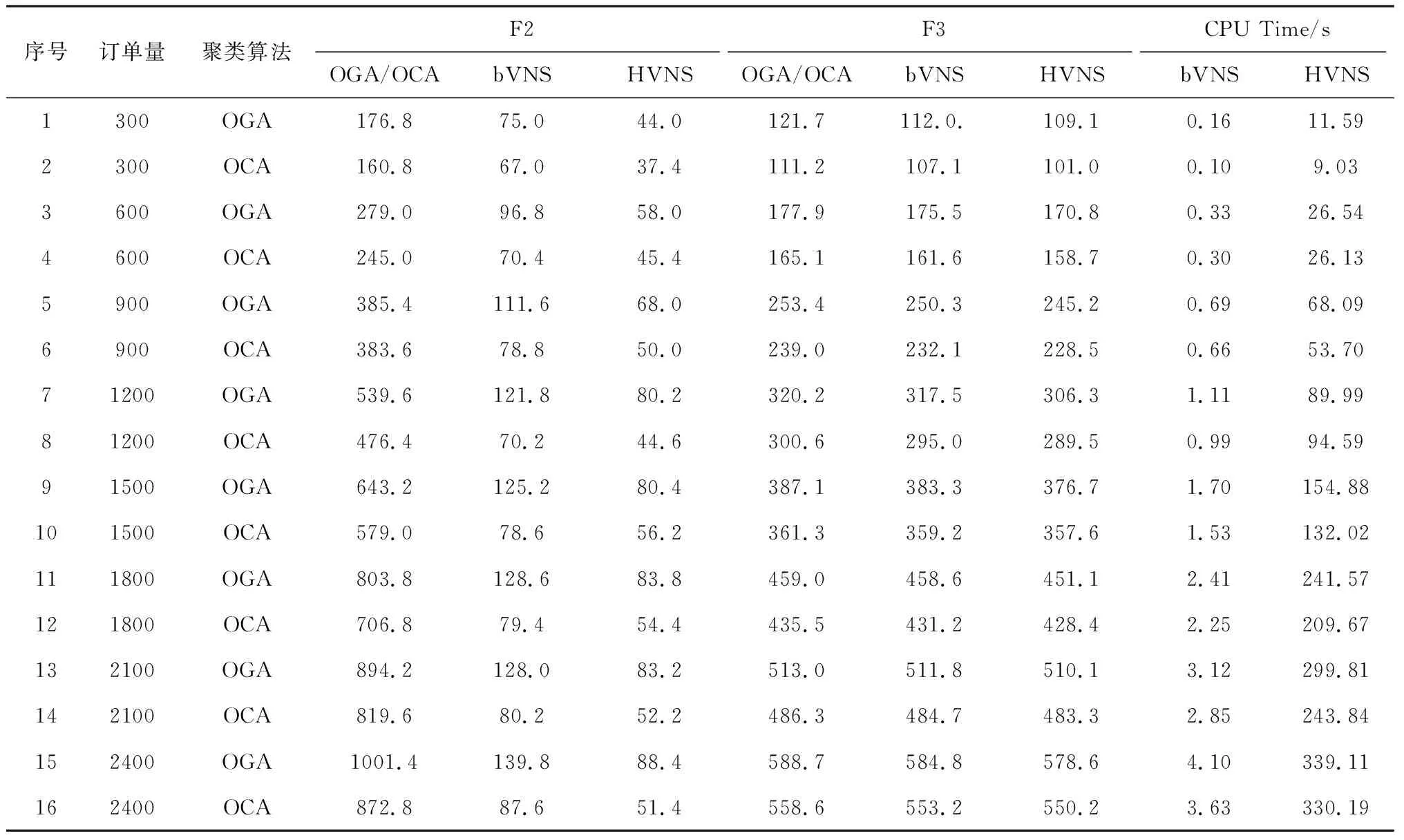
4.2 实验结果与分析
5 结语

