不同断面的巷道对爆破地震波的响应规律数值分析

袁 伟，金解放，王 杰，梁 晨，郭钟群

(江西理工大学建筑与测绘工程学院，江西 赣州 341000)

目前，在矿山巷道开挖、交通隧道掘进、水工隧洞建设等工程中，爆破开挖仍然是一种常用的、有效的施工方法。鉴于我国隧洞建设频繁、既有数量庞大的特点，在爆破工程中，经常遇到爆破近场存在既有洞室的情况。为了最大限度地降低爆破活动对既有洞室的不利影响，需要对既有洞室的响应规律进行分析研究，以确定合理的爆孔位置、爆破装药量、安全距离等技术参数，并及时对既有洞室采取有效支护措施[1]。

爆破冲击对既有洞室的影响规律，其本质是应力波的传播问题。应力波在传播过程中，遇到介质材料性质、几何性质突变时，传播规律将发生变化。爆破地震波越过巷道的迎爆侧时，一部分发生反射，另一部分将在洞室周围发生衍射和绕射，这就使得洞室周围一定的区域内应力分布不均，通常称其为动应力集中现象或振动速度放大现象[2]。在对圆形洞室的研究方面，易长平等[3]针对爆破地震波与邻近圆形洞室的相互作用问题，利用波函数展开法，理论推导了围岩的应力和位移表达式。爆破地震波的振动频率、洞室尺寸、围岩性质等因素，对洞壁质点振动响应均有较大的影响[4-6]。吴亮等[7]考虑了既有隧道与新建隧道的相对位置，分析了邻近隧道爆破掘进对既有隧道的影响。对于工程场地存在既有地下圆形洞室群的情况，梁建文等[8]研究表明当洞室间距较近时，地下洞室群的动应力集中效应显著增大。在直墙拱洞室的研究方面，成果相对较少，杨年华等[9]指出，最大振动速度出现在爆破振动波正入射部位的墙壁和拱部，而墙脚点振动速度较小。王光勇等[10]研究了纵波入射角度对地下洞室围岩动应力集中系数的影响。

在地下工程结构中，为适应工程场地实际的竖向、侧向地压分布，洞室的断面往往形式多样。而应力集中现象与孔洞的形状密切相关[11]，洞室的断面形式不同，围岩区的动应力集中程度和分布情况均会有所差异。为了更加准确地控制爆破地震波对既有洞室的不利影响，需要分析不同断面形式的洞室对近场爆破地震波的响应特点，相关研究鲜有报道。

因此，本文将利用FLAC3D软件，建立圆形、椭圆形、矩形、直墙半圆拱形和直墙圆弧拱形五种典型断面形式的矿山巷道数值模型[12]。前三种是基本断面，后两种为组合式断面，本文称圆形、椭圆形和矩形巷道为基本式断面巷道，其他为组合式断面巷道。对正入射爆破地震纵波作用下，不同断面巷道的围岩振动响应进行计算。对比分析洞壁不同部位和围岩体内部质点振速的大小、分布差异,并考虑不同频率爆破地震波下，各种巷道围岩振动响应的变化差异。

1 数值模型

1.1 模型假设

由于涉及的影响因素较多，爆破地震波在巷道围岩介质中的传播是一个比较复杂的问题。鉴于本文的研究重点在于巷道断面的几何性质对围岩质点振动响应的影响规律，因此，可以对实际的问题进行合理地简化和假设。

针对本文拟建立的数值计算模型，在保证结果不失一般性的前提下，提出如下假设：假设一,传播至既有巷道迎爆侧的爆破地震波为平面应力波，且为正入射，即入射角为0°；假设二,围岩体完整性较好，不存在大规模的结构面、裂隙等缺陷；假设三,以围岩体为主要分析对象，暂不考虑巷道衬砌结构的响应。

1.2 模型建立

采用有限差分程序FLAC3D，分别建立断面为圆形、椭圆形、矩形、直墙半圆拱形和直墙圆弧拱形的巷道-围岩体模型，其中椭圆形断面的长轴位于洞宽方向，如图1(a)所示。各模型的尺寸均为100 m×2 m×100 m，巷道洞高为6 m,除椭圆形巷道洞宽为8 m外，其他模型为6 m。直墙半圆拱形巷道的边墙高为3 m，直墙圆弧拱形巷道边墙高为4 m。直角坐标系的x、z轴分别与模型的水平、竖向对称轴重合，如图1所示。基于假设二，本文在研究应力波在围岩体中的传播时，不考虑岩石本身的能量耗散特性，且不涉及岩体的破坏过程，故围岩选用各向同性的线弹性材料模型来模拟。所输入的材料参数包括：体积模量K=6.0 GPa，剪切变形模量G=4.5 GPa，密度ρ=2 700 kg/m3。

图1 局部网格划分示意图

对巷道进深方向的位移和速度进行约束，其余外边界施加静态边界，防止边界反射波的影响以模拟无限大围岩体。在FLAC3D的Dynamic计算模块中，模型边界采用静态边界条件时，所施加的动力荷载形式只能为应力时程。拟对模型施加速度时程时，需利用式(1)将其转化为应力时程[13]。

σ(t)=-2ρcv(t)(1)

式中：σ(t)为应力时程，Pa；ρ为模型材料的密度，kg/m3；c为模型材料的纵波(或横波)波速，m/s；v(t)为质点纵向(或横向)振动速度时程，m/s。

《爆破安全规程》(GB6722—2014)[14]对矿山巷道的安全允许质点振动速度进行了规定，爆破地震波的振动频率越低，允许的安全质点振速越小，下限为15 cm/s，在计算时将输入爆破地震速度时程的峰值定为该值。一般将爆破冲击波简化为三角形波，但在考虑不同频率的谐波振动规律时，三角波的计算误差较大[6]。因此，输入爆破地震波形采用半正弦式平面应力波，频率为10～180 Hz。

由于5组计算工况中巷道的断面形式各不相同，在布置监测点时充分考虑了断面的特点。以直墙圆弧拱形巷道为例，监测点分布在拱圈、边墙和底板三个区域。拱圈的监测点位于圆弧的六等分点；边墙的起拱处，距离底板3 m、1.5 m处，墙脚处分别布置监测点；底板上每隔1.5 m布置一个测点。规定监测点到坐标原点的连线与x轴正向的夹角为θ，如图2所示。其他断面形式巷道模型的监测点布置方式与此类似。

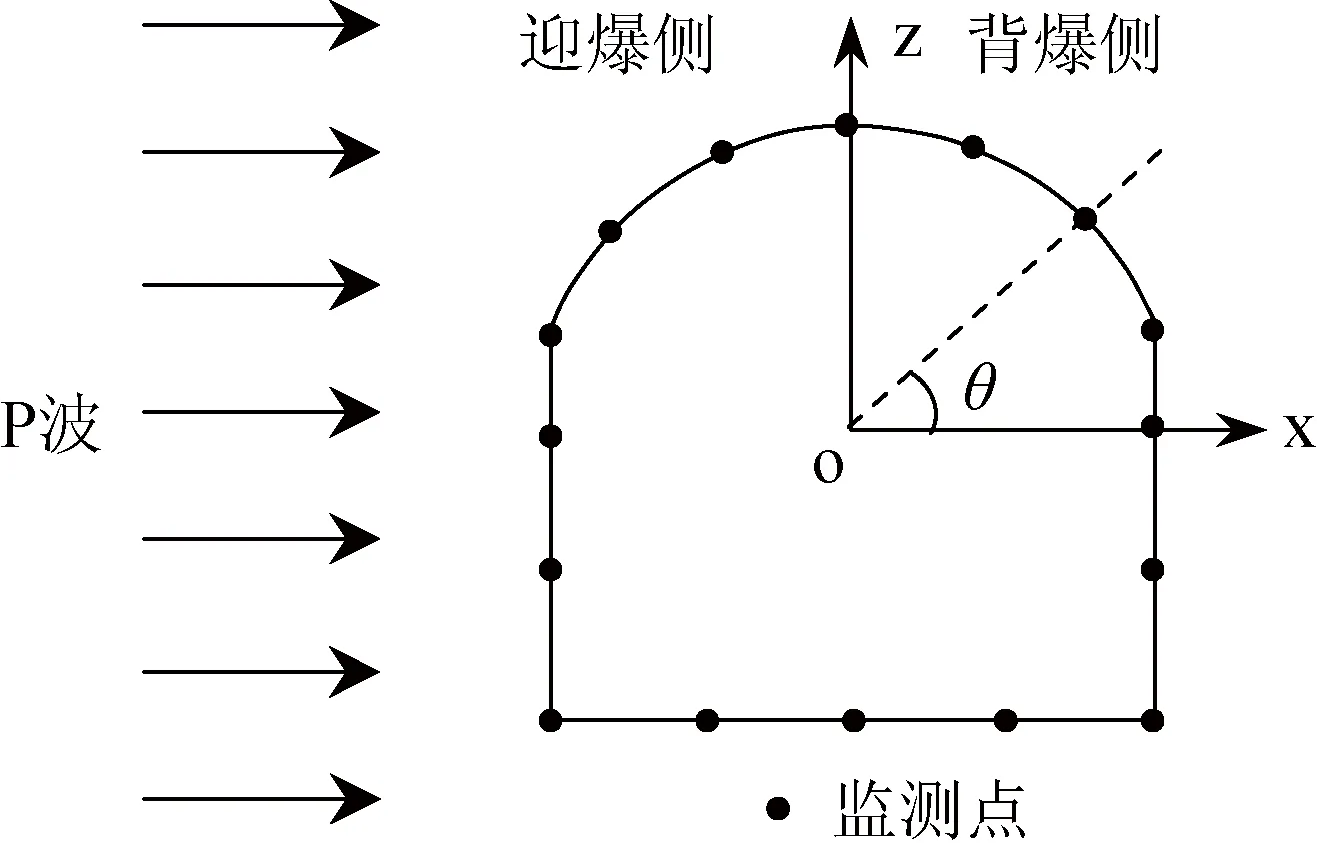
图2 直墙圆弧拱形巷道模型监测点布置示意图

2 巷道的振动速度响应规律

由于爆破地震波给既有建筑、结构物带来不利影响，规范采用安全允许质点振动速度作为评价标准；入射爆破地震波的振动频率不同，围岩安全允许质点振动速度值也不同。因此，研究爆破地震波作用下，既有巷道洞壁质点的振动速度响应具有一定的工程指导意义。

本文采用质点振速峰值放大系数来表征振动速度放大效应的强弱,其表达式见式(2)。

M=vmax/v0(2)

式中：M为质点振速峰值放大系数；vmax为质点的振速峰值；v0为输入爆破地震波的速度峰值，即震源的质点振速峰值。

2.1 洞壁质点水平振动速度响应

在爆破地震波为正入射条件下，围岩的水平振动是引发巷道损伤破坏的主要诱因。图3所示为100 Hz爆破地震波入射条件下，巷道洞壁质点的水平振速峰值放大系数(以下简称水平放大系数)分布。从水平放大系数的大小可以看出，洞壁迎爆侧的振速放大效应总是大于背爆侧，表明洞壁上越靠近震源的区域，其振速放大效应越严重。

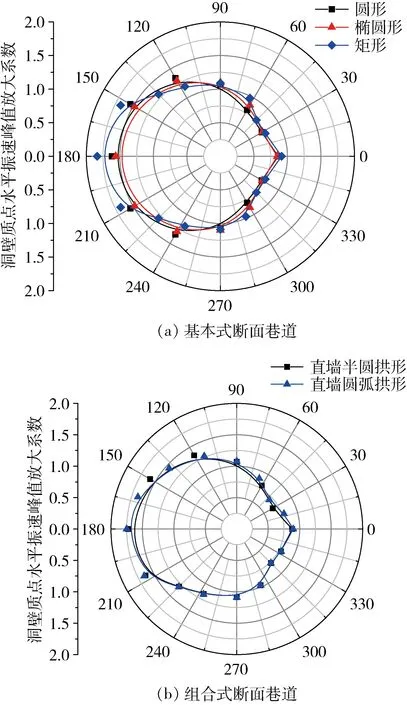
图3 巷道洞壁质点水平振速峰值放大系数分布

由图3可知，巷道断面在几何上具有上下对称性时，洞壁质点的水平放大系数也呈现出上下对称分布的特点,反之亦反。在组合式断面巷道中，由于拱圈为圆弧，质点水平放大系数的分布特征与圆形巷道类似。而边墙和底板均为直线，该处的质点水平振动响应则与矩形巷道一致。同理，直墙半圆拱形巷道的底板与直墙圆弧拱形巷道的相同，故二者底板的水平放大系数近似相等。由此可见，正入射爆破地震波作用下，组合式断面巷道的振动响应近似等于对应基本式断面巷道的振动叠加。

根据图3(a)，在同样的爆破地震波入射条件下，巷道的断面形式不同，水平放大系数沿洞壁周向的分布有较大差异。在迎爆侧，三种基本式断面巷道中，矩形巷道洞壁水平放大系数的空间变异性最大。分析认为，这与孔洞形状的缓和程度有关。根据弹性波的衍射理论[2,6]，应力波在穿越孔洞或障碍物时，将发生振动方向的偏转；孔洞的变化越缓和，振动方向的偏转变化越小，振速的变化也越小，应力集中度也越小。而在背爆侧，巷道的断面不同，水平放大系数的空间变异性差别较迎爆侧更小。

在洞壁的爆破地震波正入射点，水平放大系数表现为矩形>圆形>椭圆形。组合式断面巷道中，直墙圆弧拱形巷道的正入射点在边墙，其水平放大系数较直墙半圆拱形巷道的更大。这说明，爆破地震波正入射点位于直墙面时，所引发的振速放大效应是最强的，即迎爆侧的边墙部位是最容易发生破坏的区域。文献[9]对直墙拱形秦岭隧道的爆破振动实测结果进行了分析，其结论表明边墙是最危险区域，本文结果与其一致。

因此，为增强既有巷道抵抗爆破冲击的能力，应当对迎爆侧洞壁结构进行重点支护。当爆破近场存在直墙式巷道时，应提高对迎爆侧边墙部位的支护等级，并实时监测其动态响应。

2.2 洞壁质点竖向振动速度响应

入射爆破地震波为平行于x轴的平面应力纵波，但其通过既有巷道时，由于发生振动方向的偏转，引起了洞壁某些区域质点的竖向振动。图4所示为不同断面形式巷道的洞壁质点竖向振速峰值分布，需要说明，由于入射波中不含竖向振动成分，数据处理时无法计算竖向振速峰值放大系数。

根据图4(a)，断面的几何形状不同，巷道洞壁的竖向振速峰值沿洞壁的变化趋势是相似的，但振速峰值的大小差异较大。自迎爆侧的正入射点至背爆侧的对称位置，洞壁质点的竖向振速峰值先增大后减小，在背爆侧的洞顶和底板位置达到最大。在迎爆侧，三种基本断面式巷道中，矩形断面巷道的洞壁质点竖向振速峰值最大，椭圆形断面次之，圆形断面的最小。而在背爆侧，矩形断面巷道的洞壁质点竖向振速峰值远大于椭圆形和圆形断面巷道，且椭圆形断面、圆形断面巷道的洞壁质点竖向振速峰值较为接近。

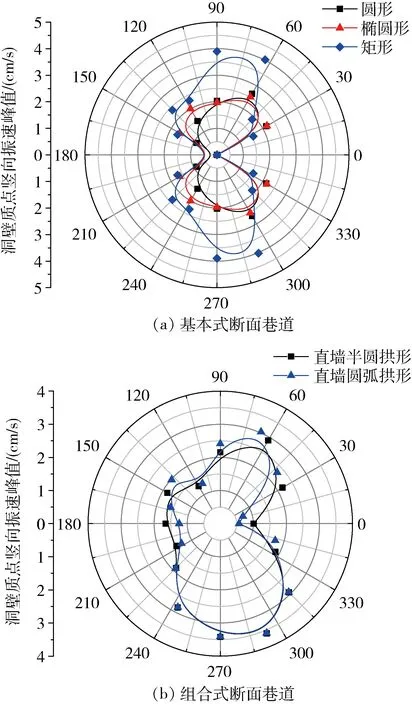
图4 巷道洞壁质点竖向振速峰值分布

由图4(b)可以看出，对于组合式断面巷道，洞壁竖向振速峰值的分布兼有圆形和矩形断面巷道的分布特点。在下半部分洞壁(x轴以下的洞壁部分)上，两种组合式断面均为折线式，洞壁竖向振动响应近似相同。在上半部分洞壁(x轴以上的洞壁部分)上，直墙半圆拱形巷道为半圆拱，直墙圆弧拱形巷道为圆弧拱+直墙，因此，两种形式巷道的竖向振动响应差异在上半部分洞壁表现较为明显。在迎爆侧的巷道起拱点处，由于直墙段到圆弧段的突变，质点竖向振动强度随之增大，并且正入射点的竖向振速峰值相较于圆形和矩形巷道有所增大。

2.3 围岩体内质点振动响应

孔洞处质点的振速放大现象具有共同的特点：集中性和局部性。集中性是指孔洞附近质点的振速远大于孔洞较远处；局部性则表明，振速放大现象主要发生在距孔洞一定范围内的区域，而在该区域以外，质点的振速近似不变。因此，邻近震源产生的爆破地震波不仅引起既有巷道洞壁的振速放大，洞壁周围一定范围的围岩体内也将发生振速的放大现象。当围岩体质点的振速达到一定值时，也会造成围岩的损伤甚至破坏，从而影响既有巷道的安全。因此，需要进一步确定爆破地震波作用下，巷道围岩的受影响范围。

图5所示为100 Hz纵波入射条件下，巷道围岩水平放大系数的空间变化情况。从图5可以看出，尽管巷道的断面形式不同，但围岩体内质点水平振速的空间变化趋势是相似的。洞壁质点的水平放大系数最大；随着围岩与洞壁距离的增加，围岩水平放大系数逐渐减小，并逐渐趋于1.0。表明围岩的响应振速峰值趋于入射爆破地震波的振速峰值，此即体现了振速放大效应的集中性。

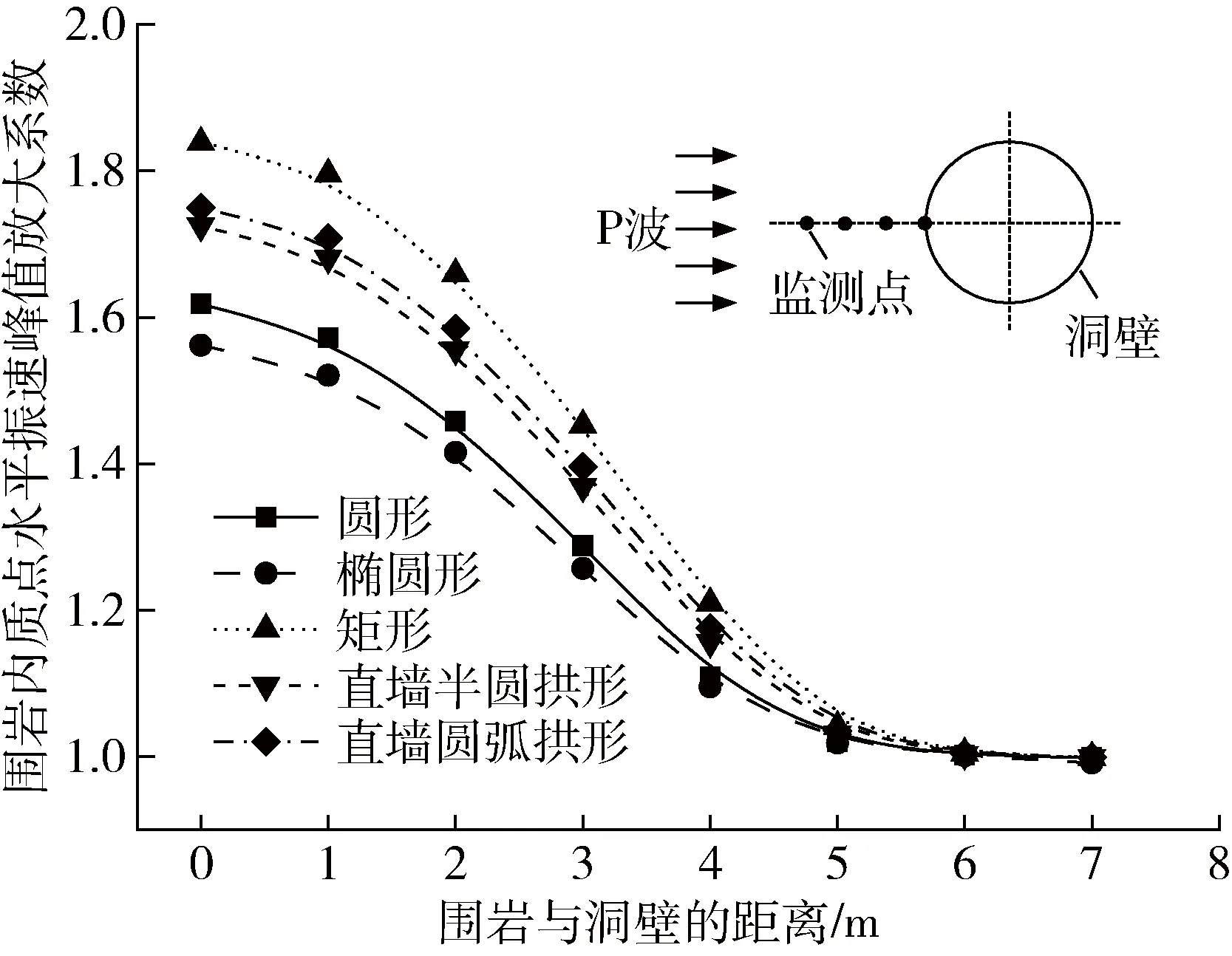
图5 围岩内质点水平放大系数

巷道围岩的水平放大系数随空间的变化可以分为三个区间：①距洞壁1 m的范围内，围岩水平放大系数较大，而变化速率较小；②距洞壁1 m至1倍洞高范围内，围岩水平放大系数快速减小，围岩质点振速逐渐接近入射纵波的强度；③1倍洞高范围以外，围岩水平振动响应接近入射爆破地震波，且基本不随空间距离而变化。此即为振速放大效应的局部性。在静力条件下，孔边应力集中主要发生在距孔边1.5倍孔径范围内[12]，相较于静力条件，爆破地震波对巷道围岩应力集中的影响范围更小。

巷道的断面形式不同，围岩内质点水平放大系数有所差异。在应力集中区内，对比三种基本式断面巷道的围岩水平放大系数，椭圆形巷道围岩水平放大系数最小，矩形巷道围岩的最大。这也表明矩形巷道围岩的水平振速随空间位置的变化率最大。对于组合式断面的巷道，围岩的水平放大系数则大于圆形巷道围岩，而小于矩形巷道围岩；直墙半圆拱形巷道围岩的水平放大系数，约为圆形和矩形巷道围岩放大系数之和的二分之一。这进一步说明，组合式断面巷道的振动响应近似等于对应基本式断面巷道的振动叠加。

综上所述，矩形断面存在明显的几何拐点，导致巷道周围一定区域内围岩的质点振速放大效应较为严重，振速随空间位置的变化幅度较大。而对于圆形和椭圆形断面，由于不存在几何上的拐点，围岩的质点振速放大效应较弱。组合式巷道围岩的振速放大效应大小介于圆形和矩形巷道之间，且拱圈的比例越大，振速放大效应越弱。

3 振动响应的频率敏感性分析

已有研究表明[3,15]，在爆破地震波作用下，洞壁的质点振速放大效应具有频率相关性，即爆破地震波的频率不同，洞壁的质点振动响应也会有差异。《爆破安全规程》中对安全允许质点振动速度的规定，也考虑了入射爆破地震波的振动频率影响。对于非圆形洞室，目前对其质点振速随入射波振动频率的变化规律研究较少。

3.1 洞壁质点水平振动速度的频率敏感性

当入射爆破地震波的振动频率为10 Hz、50 Hz、100 Hz时，巷道洞壁质点的水平放大系数分布如图6所示。由图6可知，对于任意断面的巷道，入射波的振动频率不同，洞壁质点水平放大系数的分布也不同。以矩形断面的巷道为例，振动频率f=10 Hz时，迎爆侧洞壁的水平放大系数接近于1，且迎爆侧和背爆侧的差异较小，水平放大系数沿洞壁呈近圆形分布。当振动频率提高至50 Hz、100 Hz时，迎爆侧的水平放大系数增大，背爆侧变化较小，且洞壁的质点水平放大系数逐渐偏向迎爆侧。其他断面形式的巷道，规律与此类似。

在振动频率f=10 Hz时，不同断面形式巷道的放大系数沿洞壁的分布相似，均为近圆分布。随着振动频率的提高，由断面形式不同导致的差异逐渐凸显，并且振动频率越大，洞壁质点的水平放大系数的空间分布差异越大。

取洞壁上质点的最大水平放大系数，分析其随入射爆破地震波振动频率变化的规律，如图7所示。洞壁最大水平放大系数随振动频率的变化可以分为三个阶段：快速增大、慢速增大和稳定阶段；不同断面形式的巷道，每个阶段对应的频率带宽略有差异。当巷道断面为圆形时，快速增加阶段的频率范围为10～50 Hz，慢速增加阶段的频率范围为50～150 Hz，稳定阶段的频率范围为150～180 Hz。当断面为矩形时，对应的频率范围分别为10～80 Hz、80～150 Hz、150～180 Hz。振动频率低于20 Hz时，断面形式对洞壁最大水平放大系数的影响不显著。振动频率超过20 Hz时，频率越高，各巷道洞壁的水平放大系数差异越大，表现为矩形断面的频率敏感性最强，椭圆形的频率敏感性最低。

分析认为，振动频率较低的爆破地震波，其波长较大，在洞壁处的绕射能力较强，因此洞壁质点的振速放大效应较低，且波长越大，动力扰动的效应越接近静力作用的结果[2]。迎爆侧直墙面不利于波的绕射，振速放大效应对振动频率的变化最为敏感。

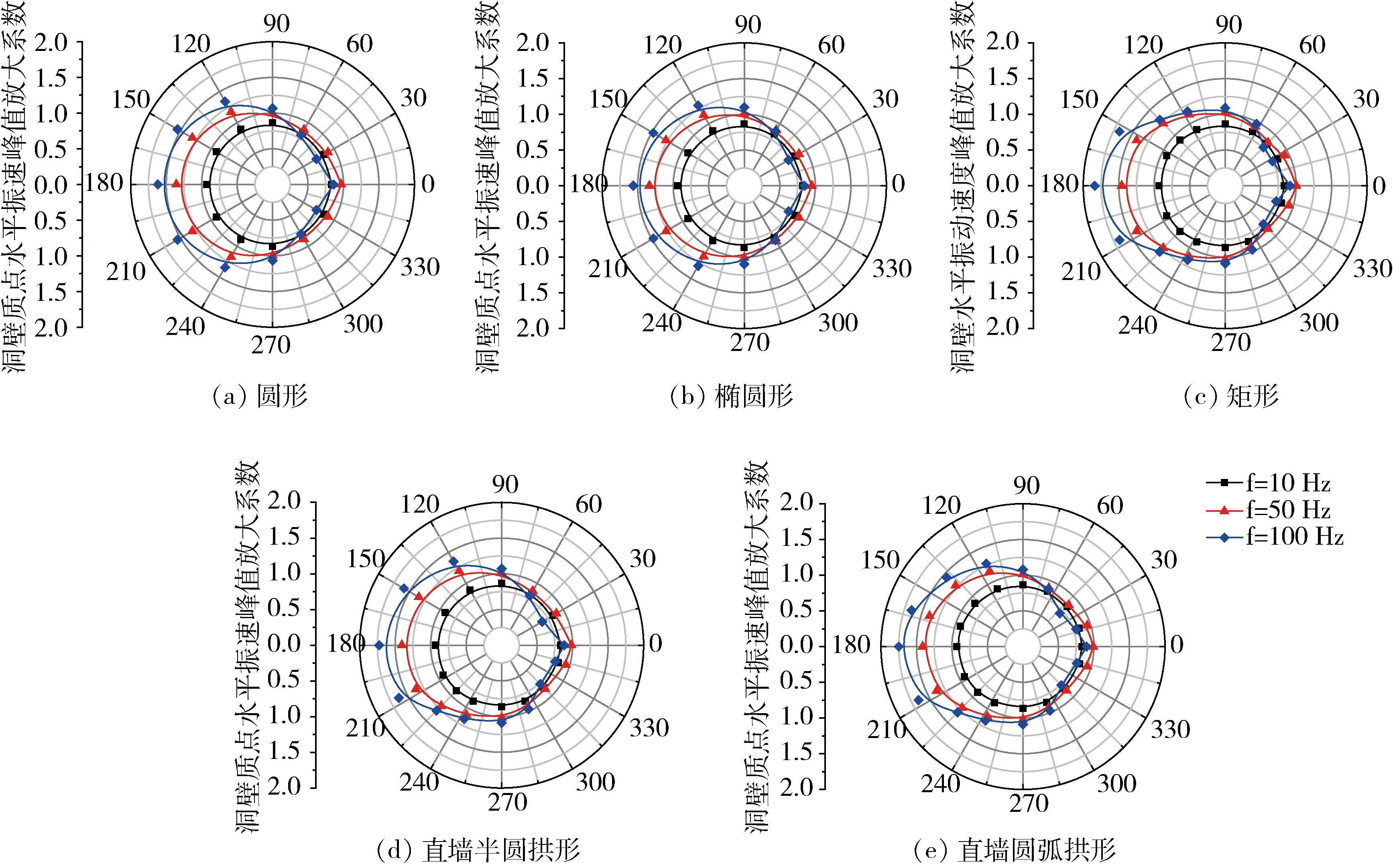
图6 不同工况下巷道洞壁质点的水平放大系数

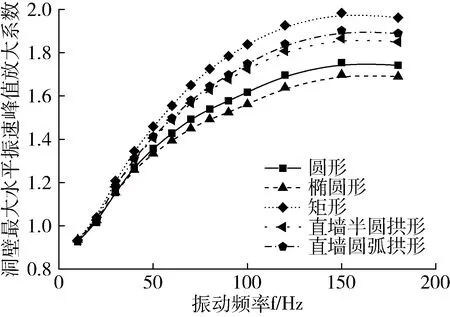
图7 洞壁最大水平放大系数随振动频率的变化

3.2 洞壁质点竖向振动速度的频率敏感性

图8所示为振动频率f为10 Hz、50 Hz、100 Hz时，质点竖向振速峰值沿洞壁的分布情况。可以看出，洞壁质点的竖向振动响应也有较强的频率敏感性。振动频率为10 Hz时，不同断面的巷道，其质点竖向振速峰值沿洞壁的分布形式类似，不具有明显的偏向性。随着振动频率的提高，洞壁竖向振动响应的分布发生较大的变化。

对于圆形巷道，振动频率的增大导致了洞壁质点竖向振动速度偏向背爆一侧，频率越大，背爆侧的竖向振动越剧烈。对于椭圆形巷道，随着振动频率的增大，质点竖向振速沿洞壁的分布，呈现了先偏向迎爆侧、后偏向背爆侧的变化特点。矩形巷道的洞壁质点竖向振动速度随振动频率的变化，也有先偏向迎爆侧、后偏向背爆侧的特征。因此，洞壁最大竖向振速出现的位置就与入射纵波的振动频率有关。

对于组合式断面的巷道，其洞壁质点竖向振动响应随频率的变化特征，可以看作基本式断面巷道的叠加。入射纵波的振动频率较高时，在迎爆侧起拱点附近，组合式断面巷道的竖向振动响应与对应基本式断面巷道有一定的差异。

图9所示为巷道洞壁最大竖向振速峰值随振动频率的变化，从中可以看出，不同频率范围内，洞壁质点的竖向振速峰值呈现不同的变化特征。在低频(10～50 Hz)范围内，洞壁质点最大竖向振速峰值随振动频率的增加而增加，增速较大但有减缓的趋势；在中等频率(50～80 Hz)范围内，最大竖向振速峰值随振动频率缓慢增加；随着振动频率的进一步提高(f>80 Hz)，洞壁质点的最大竖向振速峰值又快速增加，但较低频时增加速度更慢。

爆破地震波的振动频率对巷道洞壁质点的竖向振动影响较大。而不同断面形式的巷道，其洞壁最大竖向振速的频率敏感性也有差异，且主要体现在中低频范围内。高频扰动将引起洞壁质点较大的竖向振动，不利于既有巷道的稳定，在爆破开挖时应采取措施降低高频成分的能量。

4 结 论

1) 相同爆破地震波正入射条件下，在巷道迎爆侧，含有直墙的巷道洞壁水平振速放大效应强于圆形和椭圆形断面的巷道；在背爆侧，不同断面形式的巷道洞壁水平振速差别不显著。水平振速沿洞壁的空间变异性较直墙式巷道的大。

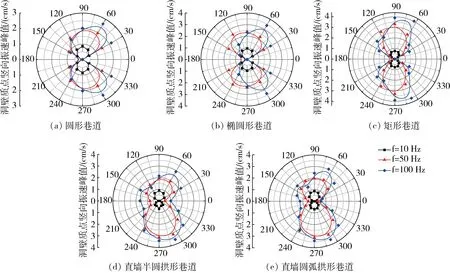
图8 不同工况下巷道洞壁质点竖向振速峰值

图9 洞壁最大竖向振速峰值随振动频率的变化

2) 洞壁质点竖向振速远小于水平振速，且最大值出现在背爆侧的顶部或底部；直墙式巷道竖向振速远大于圆形、椭圆形巷道。

3) 迎爆侧距离洞壁约1倍洞高范围内的围岩，是振速放大效应的主要影响区域，在该区域内，距离洞壁越近，围岩的质点振速越大。

4) 正入射爆破地震纵波作用下，组合式断面巷道洞壁及围岩体的振动响应特征，近似等于对应基本式断面巷道的振动叠加。

5) 随入射爆破地震波振动频率的增加，洞壁质点水平振速先增大后趋于稳定；不同频率范围内，振速随振动频率增加的速率也不同，频率越大，增速越慢。不同断面形式的巷道，其洞壁水平振速随振动频率的增加速度不同，直墙式巷道增速更大。

6) 洞壁质点最大竖向振速随振动频率的增加而增大，直墙式巷道增速更大，竖向振速沿洞壁的分布特征也随振动频率的变化而变化。

[1] 杨国梁,冯栋凯,陈高,等.中深孔爆破集成机械化施工的快速掘进方法[J].中国矿业,2015,24(7):87-89.

[2] 鲍亦兴,毛昭宙.弹性波的衍射与动应力集中[M].北京:科学出版社,1993:209-213.

[3] 易长平,卢文波,张建华.爆破振动作用下地下洞室临界振速的研究[J].爆破,2005,22(4):4-7，28.

[4] 李兴华,龙源,纪冲,等.爆破地震波作用下既有圆形隧道衬砌动应力集中系数分析[J].岩土力学,2013,34(8):2218-2224.

[5] 缪文红,王超,路世伟,等.爆破地震波作用下圆形洞室围岩振动速度分布规律[J].爆破,2016,33(4):51-54,101.

[6] 吕振利,孙金山,左昌群.爆破地震波作用下深埋圆形隧道围岩质点振动规律研究[J].现代隧道技术,2014,51(1):38-44.

[7] 吴亮,钟冬望.不同布置条件下邻近隧道掘进爆破对既有隧道的影响[J].煤炭学报,2009,34(10):1339-1343.

[8] 梁建文,张浩,WLEE Vincent.平面P波入射下地下洞室群动应力集中问题解析解[J].岩土工程学报,2004,26(6):815-819.

[9] 杨年华,刘慧.近距离爆破引起的隧道周边振动场[J].工程爆破,2000,6(2):6-10.

[10] 王光勇,余永强,张素华,等.地下洞室动应力集中系数分布规律[J].辽宁工程技术大学学报：自然科学版,2010,29(4):597-600.

[11] 徐之纶.弹性力学简明教程[M].北京:高等教育出版社,2013：75-80.

[12] 中国煤炭建设协会.煤矿巷道断面和交叉点设计规范:GB50419—2007[S].2007.

[13] 陈育民,徐鼎平.FLAC/FLAC3D基础与工程实例[M].北京:中国水利水电出版社,2011：201-202.

[14] 国家质量监督检验检疫总局，中国国家标准化管理委员会.爆破安全规程:GB6722—2014[S].2014.

[15] 孙金山,左昌群,周传波,等.爆破应力波对邻近圆形隧道的动力扰动特征[J].振动与冲击,2015,34(18):7-12，18.