基于中国剩余定理的动态门限签名方案
王 岩,侯整风,章雪琦,黄梦洁
0 引言
1979年,Shamir[1]首次提出了秘密共享的概念,并给出了一种基于Lagrange插值定理的(t,n)门限秘密共享方案,秘密被分发给n个成员,任意t个成员可以合作恢复秘密,而少于t个成员无法恢复。在已有的秘密共享方案中,大多使用Lagrange插值定理实现秘密共享[2-4]。1983年,Asmuth和Bloom[5]提出了一种基于中国剩余定理(Chinese Remainder Theorem, CRT)的门限秘密共享方案,与方案[1]相比,具有较小的计算量。随后,人们对基于CRT的秘密共享展开了深入的研究[6-8]。然而,在上述方案中,成员的份额一经分发便不再改变,难以抵抗移动攻击。
1991年,Ostrovsky等[9]提出了移动攻击的概念。移动攻击是指攻击者破获一个成员份额后,将攻击目标转移到系统中的另一个成员上,最终可在有限时间内破获t个成员份额从而窃取秘密。Herzberg等[10]基于Lagrange插值多项式,提出了先应式秘密共享(Proactive Secret Sharing, PSS)方案,能有效抵抗移动攻击。该方案在不改变秘密的前提下定期更新成员份额,攻击者需要在一个周期内攻破t个份额才能获取秘密,这是极其困难的。近年来,研究者提出了多种动态秘密共享方案。文献[11]中提出了一种代理签名方案,可在代理授权有效期内定期更新代理成员的签名私钥。文献[12]中提出了一种无可信中心秘密共享方案,该方案在异步通信系统中定期更新成员份额。文献[13]中提出了一种动态秘密共享方案,可检测并恢复被损坏的份额。2016年,文献[14]中提出了一种RSA(Rivest、Shamir和Adleman)动态签名方案,具有较好的安全性,一定程度上提高了运算效率。文献[10-14]方案均基于Lagrange插值多项式,运算量较大。
在实际应用中,成员集合可能会发生变化。针对成员加入的问题,文献[15]中提出了一种成员加入协议,在该协议中成员之间协商Shuffling因子以隐藏成员份额,需要进行大规模的秘密通信。文献[16]中提出了一个成员加入协议,但存在安全隐患,攻击者接收广播后可以很容易地恢复出老成员的私钥。文献[17-18]中提出了两种成员加入协议,但存在计算量大、理解困难、难以实现等问题。
本文基于CRT提出一种动态门限签名方案,方案无需可信中心,能够定期更新成员私钥,并保持组公钥不变,可有效防止移动攻击,并保证更新前的签名仍然有效。此外,本文方案允许新成员加入,并保证老成员的私钥和组私钥均不会泄露。与基于Lagrange插值多项式的方案相比,本文方案具有较高的时间效率。
1 Asmuth-Bloom秘密共享方案
Asmuth和Bloom[5]提出了一种基于CRT的秘密共享方案,方案主要分为三部分:
1)初始化。
假设DC为秘密分发者,P={P1,P2, …,Pn}为n个参与者组成的集合,S为共享秘密,门限值为t。DC选择大素数q和严格递增的序列d={d1,d2, …,dn},d满足如下条件:
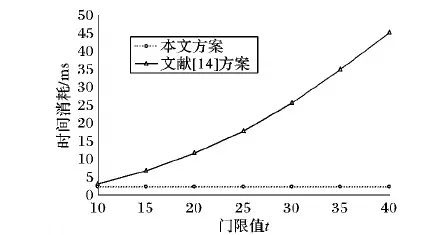
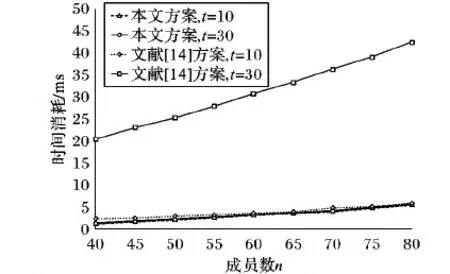
①d1 ② (di,dj)=1;i≠j; ③ (di,q)=1;i=1,2,…,n。 2)秘密分发。 Z=S+Aq Zi=Zmoddi;i=1,2,…,n 并将(Zi,di)作为秘密份额发给成员Pi(i=1,2,…,n)。 3)秘密恢复。 由中国剩余定理可解得方程组有唯一解: 其中: 可求出共享秘密S=Zmodq。 本文基于Asumth-Bloom方案[5]提出一种动态门限签名方案,方案无可信中心,成员私钥和组公钥由成员协作产生,组私钥隐式产生。方案定期更新成员私钥,可以有效抵抗移动攻击,即使攻击者在一个周期内获得了m(m 选取公共参数:p、q为两个大素数,p和q满足q|(p-1),g为有限域Zp的生成元。n为成员数目,d={d1,d2, …,dn}为单调递增的整数序列,门限为t。q和d满足Asumth-Bloom方案,n、t、p、q、g和d公开。待签名消息为M,成员私钥最多允许更新k次。 0 (1) (2) 其中:N为最小的t个di之积。 (3) 3)产生成员私钥。 (4) (5) (6) 4)Pj计算组公钥Y: (7) 事实上,完成上述步骤后,组私钥X已隐式生成: 因为xi是由Pi秘密选择的,所以除非全体成员合作,任何人都无法计算出X。 每个成员利用自己的私钥产生M的部分签名,t个部分签名可合成M的签名。 1)每个成员Pi随机选取ki∈Zp,计算并广播ri=gkimodp。 2)收到来自其他成员的ri后,Pj计算: (8) 3)Pi计算。 (9) 4)Pi计算si: (10) 将(M,r,si)作为部分签名发送给签名合成者。 5)签名合成者收到t个部分签名,计算: (11) (M,r,s)为消息M的签名。 验证者收到签名(M,r,s),使用组公钥Y验证签名: gs≡rM·r·Ymodp (12) 若式(12)成立,则签名有效。 为了抵抗移动攻击,成员定期更新各自私钥且保持组公钥Y不变。更新步骤如下: (13) (14) 3)Pi计算验证信息: (15) (16) (17) 成员私钥更新后,可按照式(8)~(11)产生签名,利用式(12)验证签名。 在更新过程中,组公钥没有改变,更新前的签名依然满足式(12),即签名依然有效。 设新成员Pn+1在第T个更新周期加入,过程如下: 1)新加入的成员Pn+1选择一个模数dn+1并公开,dn+1满足Asmuth-Bloom方案。由t个老成员Pi(i=1,2,…,t)协助Pn+1计算私钥。 (18) (19) 证明 由式(3)、(6)、(14)、(17)知,在第T(T≤k)个更新周期: 令: (20) 则: (21) 根据CRT,解同余方程组: 得唯一解: (22) 当T≤k时,由式(1)、(2)、(13)知: 当t>2时,由文献[8]可知: 根据式(10)~(11): 由式(20): 因此: rM·r·Ymodp 证明 由式(18)、 (19)知: 由式(21)~(22)知,原成员私钥: 定理3 方案具有前向安全性。 定理4 原成员Pi的私钥和组私钥不会泄露。 证明 4)本文方案中,由部分签名si合成签名S,而并非直接使用组私钥X进行签名,没有暴露组私钥X,因此组私钥X安全。 1)仿真实验。 实验环境:实验平台为Lenovo PC,Intel Core i5-2410M,2.3 GHz,Windows 7操作系统, Microsoft VC++6.0。 实验方案:文献[14]方案是一种新的基于Lagrange插值多项式的方案,与其他该Lagrange插值多项式的方案相比,该方案具有较高的运算效率,因此将本文方案与该方案进行比较。 实验1p、q、g均为十进制150位以上的整数。成员数n=50,门限值t分别取10、15、20、25、30、35、40。测试t改变时的时间性能。实验结果如图1所示。 图1 t改变时的更新时间消耗对比 随着t的增加,本文方案远小于文献[14]方案的更新时间消耗。 实验2p、q、g均为十进制150位以上的整数。门限值分别取10和30,成员数n分别取40、45、50、55、60、65、70、75、80。测试n改变时的时间性能。实验结果如图2所示。 图2 n改变时的更新时间消耗对比 在t=10和t=30两种情况下,本文方案的更新时间均较短,消耗曲线几乎重合,时间消耗与t无关。 当t=10时,文献[14]方案的更新时间消耗和本文方案较接近;但当t=30时,文献[14]方案的更新时间消耗大幅增长,时间消耗随着t的增大而显著增加。 2)更新效率分析。 在本文方案中,更新私钥计算如下: 文献[14]方案中,更新份额计算如下: 其主要时间消耗为计算t-1次多项式: gij=gi,1j+gi,2j2+…+gi,t-1jt-1 时间复杂度为O(t-1),时间消耗随门限值t增大而增大。 3)签名效率分析。 与模指数运算相比,模乘法、模加法运算的计算量可忽略不计,故通过签名和验证签名所需要的模指数运算来比较两种方案的效率。 表1为两种方案的模指数运算次数对比,从中可看出:在产生签名阶段,本文方案有t个成员共进行了t次模指数运算,相对于文献[14]方案的8t+2次,具有更高的签名效率。验证签名阶段,两种方案运算次数相差不大。 表1 两种算法模指数运算次数比较 本文基于Asmuth-Bloom中国剩余定理方案提出一种动态门限签名方案,方案定期更新成员私钥,更新后的私钥仍可进行有效签名,且组公钥不变。此外,方案允许新成员加入,成员加入时选择原有成员为其产生私钥,并保证老成员私钥和组私钥不会泄露。方案具有良好的前向安全性,能够有效地抵抗移动攻击。与基于Lagrange插值的动态门限方案[14]相比,本文方案具有较高的时间效率和较小的运算量。 参考文献(References) [1] SHAMIR A. How to share a secret[J]. Communications of the ACM, 1979, 22(11): 612-613. [2] 王洁,蔡永泉, 田有亮. 基于博弈论的门限签名体制分析与构造[J]. 通信学报, 2015, 36(5): 1-8.(WANG J, CAI Y Q, TIAN Y L. Analysis and construction for threshold signature scheme based on game theory[J]. Journal on Communications, 2015, 36(5): 1-8.) [3] 曹阳. 基于秘密共享的数字签名方案[J]. 重庆邮电大学学报(自然科学版), 2015, 27(3): 418-421.(CAO Y. Digital signature scheme based on secret sharing[J]. Journal of Chongqing University of Posts and Telecommunications (Natural Science Edition), 2015, 27(3): 418-421.) [4] DING K, DING C. A class of two-weight and three-weight codes and their applications in secret sharing[J]. IEEE Transactions on Information Theory, 2015, 11(61): 5835-5842. [5] ASMUTH C, BLOOM J. A modular approach to key safeguarding [J]. IEEE Transactions on Information Theory, 1983, 29(2): 208-210. [6] SHI N, HOU Z F, TAN M N, et al. A threshold encryption scheme without a dealer based on Chinese remainder theorem[C]// Proceedings of the 2017 IEEE 9th International Conference on Communication Software and Networks. Piscataway, NJ: IEEE, 2017: 90-96. [7] 徐甫, 马静谨. 基于中国剩余定理的门限RSA签名方案的改进[J]. 电子与信息学报, 2015, 37(10): 2495-2500.(XU F, MA J J. Improvement of threshold RSA signature scheme based on Chinese remainder theorem[J]. Journal of Electronic & Information Technology, 2015, 37(10): 2495-2500.) [8] HOU Z F, TAN M N. A CRT-based(t,n) threshold signature scheme without a dealer[J]. Journal of Computational Information Systems, 2015, 11(3): 975-986. [9] OSTROVSKY R, YUNG M. How to withstand mobile virus attacks[C]// Proceedings of the Tenth Annual ACM Symposium on Principles of Distributed Computing. New York: ACM, 1991: 51-59. [10] HERZBERG A, JARECKI S, KRAWCZYK H, et al. Proactive secret sharing or: how to cope with perpetual leakage[C]// Proceedings of CRYPTO 1995 on Advances in Cryptology. Berlin: Springer, 1995: 339-352. [11] 于义科, 郑雪峰. 标准模型下基于身份的高效动态门限代理签名方案[J]. 通信学报, 2011, 32(8): 55-63.(YU Y K, ZHENG X F. ID-based efficient and proactive threshold proxy signature in the standard model[J]. Journal on Communications, 2011, 32(8): 55-63.) [12] WANG X Q, LIN C L, LI Y. Proactive secret sharing without a trusted party[C]// Proceedings of the 5th IEEE International Conference on Intelligent Networking and Collaborative Systems. Washington, DC: IEEE Computer Society, 2013: 511-515. [13] ZHU Y S, WANG B J, CAI C. A novel smart-card based authentication scheme using proactive secret sharing[J]. International Journal of Computer and Communication Engineering, 2016, 5(3): 196-205. [14] 徐甫. 基于多项式秘密共享的前摄性门限RSA签名方案[J]. 电子与信息学报, 2016, 38(9): 2280-2286.(XU F. Proactive threshold RSA signature scheme based on polynomial secret sharing[J]. Journal of Electronics & Information Technology, 2016, 38(9): 2280-2286.) [15] LUO H Y, LU S W. Ubiquitous and robust authentication services for Ad Hoc wireless networks: TR-200030[R]. Los Angeles: University of California, 2000. [16] DONG P, KUANG X H, LU X C. A non-interactive protocol for member expansion in a secret sharing scheme[J]. Journal of Software, 2005, 16(1): 116-120. [17] 殷凤梅, 濮光宁. 允许新成员加入的无可信中心秘密共享方案分析[J]. 重庆科技学院学报(自然科学版), 2011, 13(6): 173-175.(YIN F M, PU G N. Analysis of member expansion of a secret sharing scheme without dealer[J]. Journal of Chongqing University of Science and Technology (Natural Science Edition), 2011, 13(6): 173-175.) [18] 许静芳, 崔国华, 程琦, 等. 秘密共享新个体加入协议的安全性分析与改进[J]. 通信学报, 2009, 30(10): 118-123.(XU J F, CUI G H, CHENG Q, et al. Cryptanalysis of a non-interactive protocol for member expansion in a secret sharing scheme[J]. Journal on Communications, 2009, 30(10): 118-123.) This work is partially supported by the National Natural Science Foundation of China (61572167), the Natural Science Foundation of Anhui Province (1608085MF141).



2 本文方案
2.1 产生成员私钥并计算组公钥






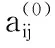
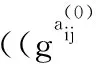
2.2 产生签名

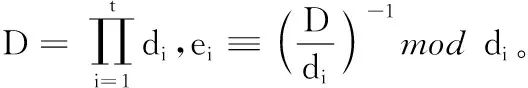
2.3 验证签名
2.4 更新成员私钥
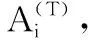
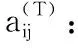

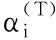

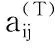


2.5 成员加入
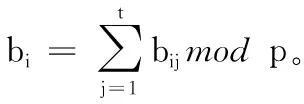


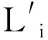
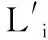

3 方案分析
3.1 有效性分析


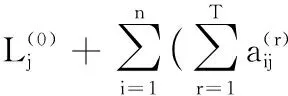
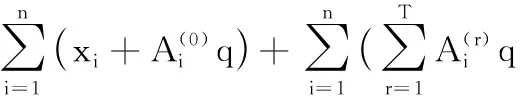

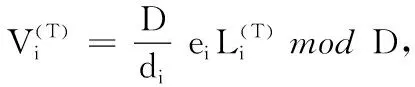

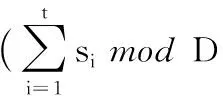

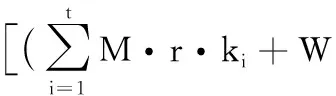




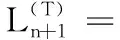
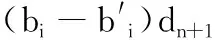
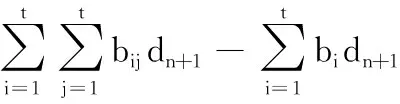



3.2 安全性分析
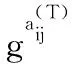
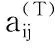
4 效率分析
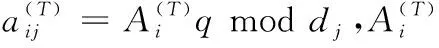

5 结语

