PID补偿的完全在线序贯极限学习机控制器在输入扰动系统自适应控制中的应用

张立优,马 珺,贾华宇

(1.太原理工大学 物理与光电工程学院,山西 晋中 030600; 2.太原理工大学 信息工程学院,山西 晋中 030600)(*通信作者电子邮箱tdliyou@163.com)

0 引言

近年来,随着智能控制的发展,基于网络学习的自适应控制方法[1-3]广泛应用于复杂系统的控制当中。自适应控制不需要很多的系统信息,就能实现复杂系统的有效控制，因此设计者对此进行了许多研究,并且提出了多种自适应控制算法。

最早的神经网络控制器参数学习算法都是采用误差反向传播(Back Propagation, BP)算法[4],控制器的参数通过系统输出误差反向传播来进行修正,以实现最终的期望输出。但是BP算法在调整自适应控制器参数上存在很多的不足。首先,BP算法极容易使训练得到的网络参数陷入局部极值，这就使得设计者在使用BP算法调整控制器参数时,必须考虑其他的优化算法来解决局部最优的问题。比如,采用遗传算法(Generic Algorithm, GA)[5]全局搜索控制器最优参数值,以实现控制器的控制要求；但是这种控制器设计复杂,且不能满足在线调节的需求。其次,BP算法在训练方式上不支持在线学习的功能,且在样本数很大时,表现出训练耗时、控制效果差等现象。为此,通过改变BP神经网络的结构,采用单隐层前馈神经网络(Single-hidden-Layer Feedforward neural Network, SLFN)来训练样本的极限学习机(Extreme Learning Machine, ELM)算法[6-7]大大提高了训练样本的速度,满足神经网络离线快速学习的要求,但仍不能够满足系统在线自适应控制的要求。为了实现在线神经网络学习的功能,文献[8]中提出了在线序贯极限学习机(Online Sequential Extreme Learning Machine, OS-ELM)算法,基于此算法的自适应控制器具备设计简单、学习速度快等优点,逐渐成为网络学习控制器参数学习的主要算法。

但是,OS-ELM算法在实际系统控制中仍存在一些问题,从而不能直接运用在实际控制当中。首先,通过OS-ELM算法的学习不一定能得到控制器参数,会使控制器输出异常。于是文献[9]中提出了正则化在线序贯极限学习机(Regularized OS-ELM, ReOS-ELM)算法,在初始化阶段,对参数表达式中的逆矩阵进行正则化处理,用于解决控制器参数无解的问题。其次,在复杂的系统中很难获取用于初始化的样本,从而无法完成神经网络的训练,对控制器的输出产生影响。为此,文献[2]中提出了完全在线序贯极限学习机(Fully OS-ELM, FOS-ELM)算法,在ReOS-ELM算法的基础上,使初始化网络的权值参数为零,只保留正则化项,通过全程在线学习获取网络参数,解决了获取初始化样本难的问题。最后,在输入扰动的系统自适应控制上,OS-ELM神经网络控制器难以满足控制需求。所以本文提出了一种比例-积分-微分(Proportion-Integral-Derivative, PID)补偿的FOS-ELM控制器设计方法,在FOS-ELM控制器上增加系统输出误差的PID增量, 通过系统输出误差的PID增量将扰动对系统输入的影响反映出来,并用于控制器的决策上,能有效降低扰动对系统自适应控制带来的干扰,补偿扰动对系统输入的影响,提高了系统的可控性和稳定性。

1 ELM算法及其改进算法

为了解决梯度下降法训练BP神经网络存在的问题,Huang等[6-7]以SLFN为基础,提出了ELM学习算法。随着对ELM算法的广泛应用,演变出了许多基于ELM算法的改进算法,在基本的学习方法上都具有如下特点:1)可将训练过的历史数据固化到隐层输出矩阵当中,权值更新时,只需对新数据学习即可;2)训练速度快、受初始化影响小、泛化能力强。这些特点使它们成为网络训练的主要方法。

1.1 ELM算法和ReELM算法的学习过程

(1)

ELM算法学习的目标就是最小化样本训练误差,即为:

min ‖Hβ-T‖2

(2)

其中:

得到β的解为:

β=H+T

(3)

其中:H+为矩阵H的摩尔-彭罗斯广义逆。当矩阵HTH为可逆矩阵时,矩阵H的广义逆为:

H+=(HTH)-1HT

(4)

由于,ELM算法的训练存在过拟合风险,于是提出了ReELM算法[11-12],同时考虑了经验风险和结构风险因素[12],通过参数λ调节这两种风险的比例,其优化的目标为:

(5)

其中:λ为两种风险的比例参数。β的解为:

β=(HTH+λI)-1HTT

(6)

1.2 OS-ELM、ReOS-ELM和FOS-ELM算法的自适应控制

β0=P0H0T0

(7)

(8)

在序列学习阶段,假设获得新的训练集为Sk时,利用最小二乘法得到参数βk为:

(9)

(10)

(11)

β0=0

(12)

P0=(λI)-1

(13)

与ReOS-ELM算法的训练过程相比,FOS-ELM算法的训练只有在线学习阶段,从而在训练方式上实现了全程在线学习的功能。

以上分别就ELM算法及其改进算法在网络训练方面作简单的归纳和总结。

本文主要研究的是FOS-ELM算法及其改进算法在自适应控制中的表现,所以首先就OS-ELM算法、ReOS-ELM算法和FOS-ELM算法在自适应控制中的应用[13]作出具体说明,其中OS-ELM算法和ReOS-ELM算法的自适应控制分为两个阶段,即:初始化阶段和自适应控制阶段,其中初始化阶段和前面各算法在网络训练中的初始化阶段一样,这里不再重复说明。FOS-ELM算法的自适应控制只有自适应控制阶段。所以就自适应控制阶段作归纳和总结。

假设控制系统的动态线性模型为：

yk+1=f0[xk]+f1[xk]uk

2) 与PVC相比，PE具有介电损耗低、绝缘强度高等优良的电气性能，PE绝缘较PVC的耐寒性好、质量轻，在同等电压等级下可比PVC绝缘层的厚度小。但是，PE材质较硬、软化温度低，接触火焰时易燃烧和熔融，耐环境应力较差。PE绝缘电缆的耐热等级主要分为70 ℃和80 ℃。

(14)

(15)

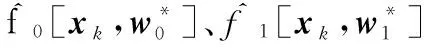
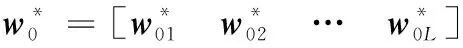
ai、bi为随机生成的常量;Δf表示模型误差,且满足sup|Δf|≤Δ,Δ为一个给定的上限值。式(15)简写为:

yk+1=Φkθ*+Δf

(16)

其中:

Φk=[G(a1,b1,xk),G(a2,b2,xk), …,G(aL,bL,xk),

G(aL+1,bL+1,xk)uk,G(aL+2,bL+2,xk)uk, …,

G(a2L,b2L,xk)uk]

(17)

化简为:

(18)

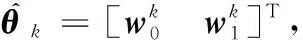
控制器设计的误差准则函数为:

(19)

(20)

其中:rk+1为系统的期望输出。

2 PID补偿的FOS-ELM控制器

通过上述分析可以发现,OS-ELM、ReOS-ELM和FOS-ELM算法之间的区别仅仅表现在算法训练中的逐级优化,而在控制器设计上没有考虑外界扰动对控制器决策的影响,这在输入扰动的系统控制中会出现控制精度下降甚至失控等现象。所以仅仅根据系统的期望输出来决策下一时刻系统的输入已达不到系统控制的要求,下面就PID补偿的FOS-ELM控制器设计进行详细说明。

2.1 PID补偿的FOS-ELM控制器设计

对此在原有的控制器学习的基础上,增加系统输出误差的PID增量来补偿扰动对系统输出的影响,在k时刻的系统输出误差及其PID增量为:

ek=yk-rk

(21)

(22)

其中:kp、ki、kd是PID增量的补偿系数；yk为k时刻系统的实际输出;rk为k时刻系统的期望输出。

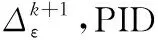
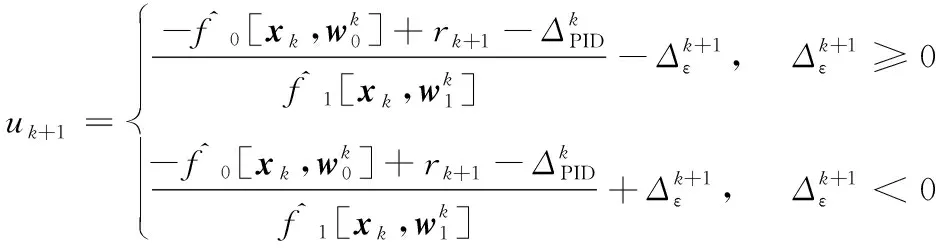
(23)

将式(23)代入式(17)中,最小化式(19),得到PID补偿的FOS-ELM控制器控制下的动态模型输出为:

(24)

其中kp=ki=kd=0。动态模型输出:

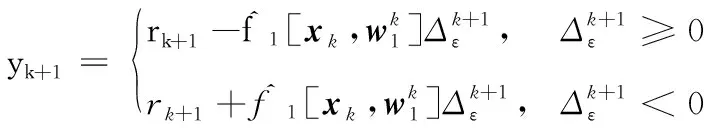
(25)

式(25)为FOS-ELM控制器控制下的动态模型输出。

2.2 控制器输出的稳定性及补偿量系数估计

假设系统的控制误差为δ,对于任意正整数k满足：

‖yk-rk‖≤δ

(26)

即:

(27)

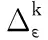
(28)

3 实验与分析

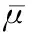
(29)

(30)

其中:ε(i)表示系统第i时刻的输出误差,i=1,2,…,300。

AFR控制系统[2]是一种单输入单输出的非线性系统,系统的输入为喷油器的喷油时间,系统的输出为发动机的AFR,为了简化问题和突出改进的FOS-ELM控制器在AFR系统自适应控制中的表现,AFR系统模型简化为:

yk+1=0.2 sin(yk)+3.5(9-uk)

(31)

AFR的期望输出是根据控制需求设置的：当燃油比为14.7时,催化剂转化效率最高；当燃油比为12.5时,发动机以最大功率输出；当燃油比为16时,实现制动的最低燃油消耗。因此本文选择的期望输出为:

(32)

在负扰动的情况下,干扰系数为η=0.2,补偿系数为(0.2,0.02,0.01),分别利用FOS-ELM控制器和PID补偿的FOS-ELM控制器对AFR系统的控制进行仿真,仿真结果如图1所示。

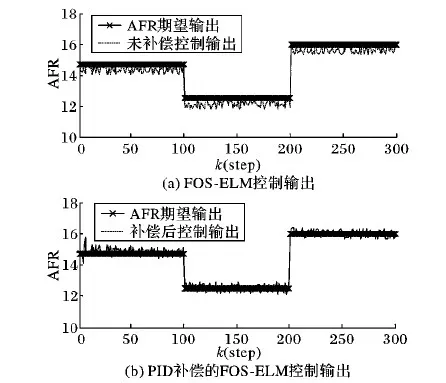
图1 负干扰下AFR自适应控制

在负扰动情况下,即Δε<0时,由式(25)知,系统的实际输出小于期望输出,根据式(21)知系统的输出误差小于0,再由式(24)知系统输出误差的PID增量能减小扰动对系统的干扰。如图1所示,图1(a)是在持续负扰动的情况下,FOS-ELM控制器控制下的系统输出,其实际输出全部低于期望输出。而由图1(b)可以看出PID补偿的FOS-ELM控制器控制下的系统输出围绕在期望输出周围,且随着控制器的不断学习,输出误差在不断减小,最后趋于稳定。当控制误差为0.4,系统输出300次,由表1可知PID补偿的FOS-ELM控制器有效控制率达到93.3%,远远高于未补偿的控制器的51.7%,控制器控制效果得到明显改善。

同样,在正扰动的情况下,干扰系数和补偿系数不变,仿真结果如图2所示。

图2 正干扰下AFR自适应控制

同样在正扰动情况下,即Δε≥0时,由式(25)知,系统的实际输出大于期望输出,根据式(21)知系统输出误差大于0,再由式(24)知系统输出误差的PID增量同样能够减小扰动对系统的干扰。如图2所示,图2(a)是在持续正扰动的情况下,FOS-ELM控制器控制下的系统输出,其实际输出全部高于期望输出。而由图2(b)可以看出PID补偿的FOS-ELM控制器控制下的系统输出围绕在期望输出周围,且随着控制器的不断学习,输出误差在不断减小,最后趋于稳定。当控制误差为0.4,系统输出300次,由表1可知PID补偿的FOS-ELM控制器有效控制率达到95.3%,远远高于未补偿的控制器的53%。

在正负扰动的情况下,干扰系数为η=0.5,补偿系数为(0.2,0.15,0.01),对AFR系统的控制进行仿真,仿真结果如图3所示。

在正负扰动的情况下,正如式(25)所描述的系统,如图3所示。从图3(a)可以看出FOS-ELM控制器的输出已经严重偏离了期望输出,无法对AFR系统进行有效控制,而式(24)所描述的系统,即由图3(b)仿真结果显示的PID补偿的FOS-ELM控制器却能够降低输入扰动对系统输出的影响,达到一定的补偿效果,在控制误差为1时,由表1知,控制器的有效控制率分别为55.3%和93.7%。

图3 正负干扰下AFR自适应控制

通过系统仿真可以看出,无论是什么类型的系统扰动,当输入扰动使得系统输出误差大于系统控制误差时,系统在FOS-ELM控制器下处于失控状态,而PID补偿的FOS-ELM控制器能够有效补偿系统输入,实现系统的有效控制。

下面就以上两种控制器在AFR系统中的有效控制时间和整体控制误差进行整理,其中,PID补偿的FOS-ELM控制器算法记为PID-FOS-ELM,结果如表1所示。

表1 不同干扰和控制算法下AFR系统的性能表现

4 结语

本文主要提出了PID补偿的FOS-ELM控制器设计方法,并将该方法应用于输入扰动系统的自适应控制当中,结合FOS-ELM算法的在线学习能力和PID快速响应能力,在线补偿扰动下的系统输入,减小输入扰动对系统控制的影响。根据系统的控制要求,合理选择控制器的参数和补偿系数能够实现理想的控制效果。在仿真中可以看出,PID补偿的FOS-ELM控制器都能够在不同类型的扰动下作出有效的控制,明显改善基于在线学习控制器的控制性能,极大提高了系统的抗干扰能力和控制品质。

参考文献(References)

[1] CHEN F C. Back-propagation neural networks for nonlinear self-tuning adaptive control [J]. IEEE Control Systems Magazine, 1990, 10(3): 44-48.

[2] WONG P K, VONG C M, GAO X H, et al. Adaptive control using fully online sequential-extreme learning machine and a case study on engine air-fuel ratio regulation [J]. Mathematical Problems in Engineering, 2014, 2014: Article ID 246964.

[3] LIU Y J, CHEN C L P, WEN G X, et al. Adaptive neural output feedback tracking control for a class of uncertain discrete-time nonlinear systems [J]. IEEE Transactions on Neural Networks, 2011, 22(7): 1162-1167.

[4] LECUN Y A, BOTTOU L, ORR G B, et al. Efficient back prop [M]// Neural networks: Tricks of the Trade. Berlin: Springer, 2012: 9-48.

[5] 李敏远, 都延丽. 基于遗传算法学习的复合神经网络自适应温度控制系统[J]. 控制理论与应用, 2004, 21(2): 242-246.(LI M Y, DU Y L. Composite neural networks adaptive control system of temperature based on GA learning [J]. Control Theory & Applications, 2004, 21(2): 242-246.)

[6] HUANG G B, ZHU Q Y, SIEW C K. Extreme learning machine: a new learning scheme of feedforward neural networks[C]// Proceedings of the 2004 IEEE International Joint Conference on Neural Networks. Piscataway, NJ: IEEE, 2004, 2: 985-990.

[7] HUANG G B, WANG D H, LAN Y. Extreme learning machines: a survey [J]. International Journal of Machine Learning and Cybernetics, 2011, 2(2): 107-122.

[8] LIANG N Y, HUANG G B, SARATCHANDRAN P, et al. A fast and accurate online sequential learning algorithm for feedforward networks [J]. IEEE Transactions on Neural Networks, 2006, 17(6): 1411-1423.

[9] HUYNH H T, WON Y. Regularized online sequential learning algorithm for single-hidden layer feedforward neural networks [J]. Pattern Recognition Letters, 2011, 32(14): 1930-1935.

[10] LI X L, JIA C, LIU D, et al. Adaptive control of nonlinear discrete-time systems by using OS-ELM neural networks[J]. Abstract and Applied Analysis, 2014, 2014: Article ID 267609.

[11] DENG W Y, ZHENG Q H, CHEN L. Regularized extreme learning machine[C]// CIDM 2009: Proceedings of the 2009 IEEE Symposium on Computational Intelligence and Data Mining. Piscataway, NJ: IEEE, 2009: 389-395.

[12] 邓万宇, 郑庆华, 陈琳, 等. 神经网络极速学习方法研究[J]. 计算机学报, 2010, 33(2): 279-287.(DENG W Y, ZHENG Q H, CHEN L, et al. Research on extreme learning of neural networks [J]. Chinese Journal of Computers, 2010, 33(2): 279-287.)

[13] JIA C, LI X, WANG K, et al. Adaptive control of nonlinear system using online error minimum neural networks [J]. ISA Transactions, 2016, 65: 125-132.

This work is partially supported by the Natural Science Foundation of Shanxi Province (2015011050).