复杂网络演化的舆论动力学模型及仿真分析

王 舰,王志宏,张乐君

(1.辽宁工程技术大学 工商管理学院,辽宁 葫芦岛 125105; 2.扬州大学 信息工程学院,江苏 扬州 225127)(*通信作者电子邮箱wj26@163.com)

0 引言

舆论是社会公众在特定事件下发表个体意见及意见之间相互作用形成的观点,是人类特有的社会现象。社会个体的差异化和意见之间相互作用的复杂化决定了舆论传播动力学演化过程的复杂性,舆论动力学是复杂网络一个重要的研究方向,舆论传播的实质和内在机制是学者们一直感兴趣的重要课题,探索动力学行为对复杂网络的研究具有重要意义。

舆论观点的演化可以简化为“生”和“死”两种状态,即舆论观点产生及删除形成新连接的过程,为了合适地描述舆论的动力学演化过程，学者们进行了大量的尝试,尤其是物理学家活跃在这一领域,将统计物理的研究成果应用在舆论分析和研究中,促进了物理学和社会学等学科的发展[1]。伊辛模型是描述二元观点相变的最早常用舆论动力学模型[2]。Katarzyna等[3]提出基于社会物理学的舆论模型,基本思想原则是“三人成虎”，即具有相同意见的相邻成员间可以通过劝说采取相同态度。连续尺度上建立的Deffuant模型和HK(Hegselman-Krause)模型是有限劝说模型,即观点接近的人容易交换意见,通过测定个体意见距离,设定信任阈值并逐渐实现观点接近[4]。Galam[5]提出以少数服从多数为原则的选举模型,该模型的适用性更广泛,可以用于解释群体决策过程、恐怖主义和舆论演化等现象。刘慕仁等[6]借用计算机技术采用定性模拟元胞自动机方法进行舆论演化仿真。

在复杂网络的舆论研究中,Zenette[7]首次将流行病模型应用在小世界网络传播上,用数值定量表征小世界网络的演化过程。Fortumato[8]研究了无标度网络中引入HK模型分析特定扰动情况下舆论的变化情况。Nekovee等[9]使用平均场方程的解来描述随机网络模型和无标度网络模型演化和传播中的阈值问题,研究结果表明无标度社会网络比随机网络更易于舆论的传播。崔爱香等[10-11]从网络的局部结构角度提出共邻居驱动的网络演化模型,并在此基础上针对网络演化考虑加速增长这一重要因素,提出改进的Holme-Kim模型,数值模拟结果可以再现真实网络的低阶幂律集团分布特性。Zhao[12]在复杂自适应系统理论和复杂网络方法基础上进行仿真实验,结果表明小世界连接概率小于指定阈值时可以通过协商达成共识,当概率大于指定阈值时舆论的存在时间将明显降低,大众媒体及诸多因素会影响舆论的演化过程。吴云等[13]通过HK模型中引入E指标来构建舆论演化模型,研究规则网络上的舆论动力学演化情况。

本文在现有研究基础上,以复杂网络舆论动力学为理论基础,建立动力学模型并引入Fokker-Planck方程描述舆论动态演化过程求出稳态解决方案和静态解,利用计算机仿真来解析基于复杂网络舆论的形成和演化过程,以微博舆论事件真实数据为基础运用模型从实证角度研究,更准确客观地了解舆论扩散的过程。

1 复杂网络舆论模型

1.1 舆论模型

设v为每个节点(在复杂网络中每个个体都视为一个节点,因此本文将统称为节点)的一个意见,将意见组合起来其边界两端就是极端相反的意见,v在边界的闭合子集中不断变化;设l为意见的连接数量,该值为离散变量,取值范围在0和最大数之间变化。这里的最大数通常指某个固定值,比如小于网络规模n个数量级的值。

设f为密度函数的演化方程:

f=f(v,l,t);f:V×L×R+→R+

(1)

其中:v∈V(V∈[-1,1])是意见变量;l∈L并且满足L={0,1,…,lmax},是描述连接数量的离散变量;t∈R+是常见的时间变量。对于每个时间t≥0可以计算出以下边际密度:

(2)

连接数量的演化等价于网络的度数分布,假设节点个数是守恒的,即

(3)

总体舆论意见分布定义成边际密度函数为:

(4)

从微观角度描述节点是以二元相互作用和连接数来修改意见的,如果两个节点的意见和连接数，即(v,l)和(v*,l*)相遇,那么舆论意见交互之后变为v′和v*′,并且交互之后的意见取值范围为V∈[-1,1]。函数的时间演化方程由玻尔兹曼方程表示:

(5)

其中:τ[·]表示与网络连接演化相关的算子；Q(·,·)表示二元互动算子。计算获得公式的弱形式[14]如下:

(6)

其中“〈·〉”表示随机变量的期望值。

1.2 舆论演化模型

关于舆论演化过程,Barabási等[15]提出复杂网络中边的添加和删除过程与静态无标度严格相关。本文在网络动态描述中设定算子τ[·]是节点在离散空间中连接演化模型中的一个细节,τ[·]通过优先连接组合来定义表达式,以网络中删除和添加边的方式来描述连接演化的过程。

对于每一个l=1,2,…,lmax-1定义如下:

(l+α)f(v,l,t)]

(7)

其中:α,β>0是吸引系数;Sd(f;v)≥0是移除链接概率;Sa(f;v)≥0是添加连接的速率,并且很多研究表明移除和添加一般是成对出现的；ω=ω(t)表示平均连通密度。ω(t)的定义如下:

(8)

式(7)描述的是节点之间连接变化导致的f(v,l,t)净增量，其边界定义如下:

(9)

式(9)中应该考虑到两种事实存在情况,即：节点间为0个连接时不能被移除；节点间连接达到最大值时不能再添加。

如果定义特征速率为:

(10)

其中:

(11)

假设τ[·]中的节点总数是守恒的,考虑到式(8)中的平均连通密度ω的演化情况,对平均连通密度演化得出对于每一个t≥0有:

(12)

通常情况下ω是不守恒的,当吸引系数β=0时逐渐达到守恒状态,如果Sd=Sa的条件下特征率由式(11)给出并且设定Ud=Ua时,密度函数f(v,l,t)以足够快的速度衰减。

对于节点守恒数设定:

(13)

满足式(10)所需要的条件时则能够得到节点总数守恒公式如下:

(14)

有一种特殊情况,就是Sd和Sa是常量,此时算子τ[·]是线性的,由T[·]表示,网络连接的演化不受舆论意见变化的影响，得出公式为:

(15)

其中:

(l+α)ρ(l,t)]

(16)

式(16)的动力学方程对应择优连接过程(α,β≈0)和统一过程(α,β>0)的连接密度函数为ρ(l,t)。由于复杂网络连接的特性,一般在Sd=Sa,β=0的线性情况下可以证明由ω表示连通密度的渐近性。

设对于每一个l∈L,静态解等价于:

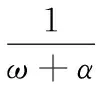
ω(l-1+α)ρ∞(l-1)]

(17)

进而得到:

(18)

其中:

(19)

在α≥1和α=0的情况下会进一步得到近似解,对于α取值10的正指数时,在式(16)描述的优先连接过程被损坏,并且网络近似为度分布服从泊松分布的随机网络,在实际情况中,α的极限值趋近于正无穷时,得到:

(20)

其中e是自然常数,对于ω≥1和α取值10的负指数情况,密度分布可以准确地近似为单一指数截断幂律,即表示为:

(21)

1.3 Fokker-Planck方程

Fokker-Planck方程是描述粒子在受到某个随机力后随着时间演化的位置和速度分布的函数,由荷兰和德国物理学家的名字命名而来。舆论动力学演化方程的一般形式很难得到大时间行为分析结果,通过引入Fokker-Planck方程[16]的简化形式构建模型,以对舆论动力学进行更全面的分析。

在变量v变化较小的情况下来分析舆论演化分布的Fokker-Planck微分方程,为了构建接近真实的舆论动力学模型,需要考虑很多约束条件,D(v)是量化个人行为意见的偏差和不确定因素的干扰函数,Κ[f]是表示舆论演化过程不可预测的修改存在随机性,则Fokker-Planck方程满足:

(22)

某种情况下会得到稳态解决方案如下:

f∞(v,l)=g∞(v)ρ∞(l)

(23)

其中ρ∞(l)是网络中部分连接的稳态分布,则上述方程的渐近解如下:

(24)

则满足方程:

(25)

其中Κ[f]根据财富分配、社会知识和意见传播等不同研究内容有不同的表达式[17],本文设定Κ[f]=κv和D(v)=1-v2经过变换得到方程静态解如下:

(26)

其中：C0是使g∞总量保持为1的常量。

1.4 复杂网络中的舆论动力学

社会生活的各个领域中不同系统基本上都可以用复杂网络进行描述,包括与我们生活紧密相关的通信网络、交通网络、人际关系网络等,可以毫不夸张地说我们已经置身在各种网络之中。人与人的沟通和意见的交流衍生出巨大的社会关系网络,人是网络中的节点,人与人之间的交流构成了连线即边,意见是不同的,每一个人拥有一个意见值即舆论值,意见之间是相互影响的,这个过程就是舆论动力学的演化过程。

舆论动力学主要研究的是社会经济系统中个体之间意见与外界信息之间的相互影响,个体之间所持有的观点之间的形成与演化现象,因此基于复杂网络的舆论观点形成演化过程也属于动力学的研究范围。1.3节提到的动力学方程及解的静态形式,用程序表达并进行仿真分析,筛选出微博上发生的典型舆论事件并抓取和处理数据,得到仿真实验需要的参数信息,通过仿真分析结果研究舆论演化模型和复杂网络的关系,通过Fokker-Planck方程仿真结果分析舆论意见分布情况与舆论传播的关系,以“湖北荆州电梯吃人事件”为例,通过实证研究探索舆论模型分析的可行性。

2 仿真与分析

本文分别对建立的舆论演化模型及Fokker-Planck方程静态解进行仿真实验,以图形来说明舆论变化情况,在仿真分析基础上将模型应用到具备复杂网络特性的微博舆情事件转发网络中进行实证分析,以验证舆论演化模型和Fokker-Planck方程分析的可行性。

2.1 仿真模拟

对舆论演化模型进行模拟,当α值取10的正指数情况下参数取值如表1,对式(15)的静态解仿真模拟如图1所示。

表1 α 值取10的正指数时参数取值

由于舆论连接数量的演化等价于网络的度数分布,因此图1可以近似为泊松分布,当α取值为10的正指数时的度分布可以推测出网络为随机网络或者小世界网络。

吸引系数α值取10的负指数时则参数变化范围为:α=(10-1,10-2,10-3),对式(15)的静态解收敛到幂律分布的仿真模拟如图2所示。

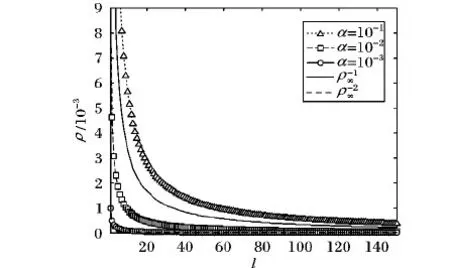
图2 α取值10的负指数静态解仿真模拟图

图2中随着意见连接数量的增加,连接度绝大多数比较小,只有少数个体值较大近似为幂律分布,具备这种度分布特性的网络判断为无标度网络,这种特性可以反映舆论意见连接网络的生长和演化过程。在舆论传播过程个体节点的度是不均匀的,且起决定作用的是关键(富)节点,随着舆论的演化,关键(富)节点的度值越来越大,呈现“富人俱乐部”现象。

为了验证Fokker-Planck方程的简化形式可以分析舆论意见分布情况与舆论传播间的关系，对稳态解决方案的静态解仿真得到如图3所示的意见分布曲线。

图3 Fokker-Planck方程静态解仿真模拟图

Fokker-Planck方程静态解的仿真结果显示的是舆论意见的分布,呈现正态分布是指消极和积极态度的人均占据少数,保持中立意见的人数占多数;呈“M”形分布是指保持中立意见的人数较少,而消极和积极态度的占多数,并且双方人数势均力敌。σ系数取值不同会对舆论意见分布有影响,取值越小,正态分布情况越多。

2.2 实证分析

微博舆论传播已经被很多文献研究并且证明其具备无标度网络属性,本文选取2015年7月发生的“湖北荆州电梯吃人事件”(简称D事件)作为分析案例,设置相应的参数进行分析。截止2017年初D事件共获取到275条转发信息,对数据信息进行筛选后得到D事件共260个微博用户作为节点和263条边,节点度如图4所示服从幂律分布,网络中大多数节点的度相对较低,只有小部分节点的度值相对较高,因此可以判定D事件舆情转发网络具有复杂网络无标度特性。

图4 D事件转发网络度分布

因此动力学方程中的l最大连接数量为263,平均连通密度ω设置为网络平均度2.033,由于动力学描述过程中提到连接数量的演化等价于网络的度数分布,因此取α较小值,则得到仿真方程为:

(27)

由于ω=2.033>1,因此表达式可以近似写成如下形式:

(28)

对式(28)进行仿真，得到如图5所示的仿真结果。

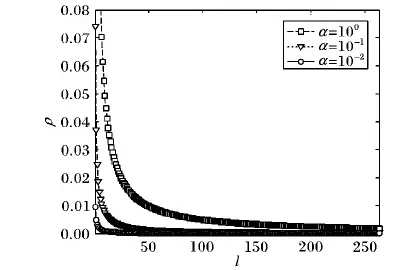
图5 微博舆论事件数据模拟静态解仿真图

从图4～5度分布情况可以判断微博舆情事件的传播网络具备幂律分布的无标度特性,通过对ω的调试可以知道它的变化程度对曲线的影响很小,因此在舆论形成和演化过程中,网络的平均连通密度对边际密度的影响很小;通过对吸引系数α的调试可以看出,值越大曲线下降得越缓慢,说明舆论消息内容的吸引力对舆情传播和演化会产生影响,因此多数网络上传播的微博信息能够演化成舆论并且被广泛传播是其自身消息内容与个体的联系更紧密、更加吸引个体参与互动等原因所致。

网络演化包含诸多因素比如系数、规模和结构等,每一种因素的变化都会对舆论演化模型静态解的仿真结果产生影响,如表2所示,可以通过图5～6对比4种网络的仿真模拟图,直观上了解曲线形状的差异。

表2 仿真用例和其他文献研究用例对比

图6 其他文献仿真用例图

通过仿真用例与其他文献用例的对比分析可以发现,多数静态仿真模拟曲线并不是严格意义上服从泊松分布或幂律分布,曲线结构会有多种形式,需要在后续研究中不断调试参数及总结产生不同曲线的原因。

通过引入Fokker-Planck方程静态解得到网络演化和舆论分布双重作用下稳态解决方程f∞(v,l)=g∞(v)ρ∞(l)的仿真模拟曲线如图7所示。

意见连接数量和舆论意见共同作用,形成了舆情事件传播曲线,D事件中个体意见链接数量的增加会导致节点度数不断变化,“富人俱乐部”现象就会形成,但是俱乐部系数的值没有达到1,也说明此网络不是完全连通图。

图7 舆论动力学静态解决方案模拟图

图7中舆论意见态度呈现正态分布表明中立态度较多,极端意见占少数,在微博舆论事件中多数个体是不带感情色彩的转发,观望者居多,而这些少数极端意见的发布者人数虽然不占据优势,但在网络中地位却是举足轻重的。

3 结语

传播动力学模型是过去十年比较领先的建模方法,将动力学理论引入舆论研究中用于了解舆论现象的形成与扩散,表述个体之间意见交流的微观相互作用机制。舆论传播所形成的复杂网络具有大时间行为,充分考虑舆论意见是随着时间不断变化的大规模复杂网络,运用动力学方程可以描述节点意见之间不断发生的变化情况及舆论意见更新与新连接创建和删除过程相结合,通过引入Fokker-Planck方程对意见变化情况更全面地描述并介绍可变扩散系数及边界的存在,了解舆论意见形态的渐近行为,简化计算方程并分析稳态解决方案；通过演化方程的分析得到渐近行为与泊松分布和截断幂律分布相一致,舆论意见的传播会受到节点数量的影响,节点之间的连接方式也会受到节点意见的影响的结论；运用仿真数据对模型进行模拟并在此基础上以新浪微博上发生的真实舆论事件数据进行实证分析,结果充分表明此模型的有效性。

在舆情危机四伏的互联网时代对舆论动力学模型的研究可以帮助理解舆论演化过程,用数字和图形更直观地表达出舆论变化形式,进而探索如何疏导和控制舆论走向有益的一面,寻求抑制网络谣言和解除舆情危机的策略方法以帮助企业和国家传播正能量信息。

参考文献(References)

[1] 刘怡君, 李倩倩, 朱文元.舆论动力学模型综述[J]. 管理评论, 2013, 25(1): 167-176.(LIU Y J, LI Q Q, ZHU W Y. Review of public opinion dynamics model[J]. Management Review, 2013, 25(1): 167-176.)

[2] BODINEAU T, GRAHAM B, WOUTS M. Meta stability in the dilute ising model [J]. Probability Theory and Related Fields, 2011, 157(3/4): 955-1009.

[3] KATARZYNA S-W, JOZEF S. Opinion evolution in closed community [J]. International Journal of Modern Physics C, 2000, 11(6): 1157-1165.

[4] HEGSELMANN R, KRAUSE U. Opinion dynamics and bounded confidence models, analysis and simulation [J]. Journal of Artificial Societies and Social Simulation, 2002, 5(3): 12-16.

[5] GALAM S. Minority opinion spreading in random geometry [J]. The European Physical Journal B: Condensed Matter and Complex Systems, 2002, 25(4): 403-406.

[6] 刘慕仁, 邓敏艺, 孔令江.舆论传播的元胞自动机模型(Ⅰ) [J]. 广西师范大学学报(自然科学版), 2002, 20(2): 1-4.(LIU M R, DENG M Y, KONG L J. Cellular automata model for public opinion propagation(I) [J]. Journal of Guangxi Normal University (Natural Science Edition), 2002, 20(2): 1-4.)

[7] ZANETTE D H. Dynamics of rumor propagation on small-world networks [J]. Physical Review E, 2002, 65(4): 041905.

[8] FORTUNATO S. Damage spreading and opinion dynamics on scale free networks [J]. Physica A: Statistical Mechanics and its Applications, 2005, 348: 683-690.

[9] NEKOVEE M, MORENOB Y, BIANCONIC G, et al. Theory of rumour spreading in complex social networks [J]. Physica A: Statistical Mechanics and its Applications, 2007, 374(1): 457-470.

[10] 崔爱香, 傅彦, 尚明生, 等.复杂网络局部结构的涌现: 共同邻居驱动网络演化[J]. 物理学报, 2011, 60(3): 038901.(CUI A X, FU Y, SHANG M S, et al. Emergence of local structures in complex network: common neighborhood drives the network evolution [J]. Acta Physica Sinica, 2011, 60(3): 038901.)

[11] 崔爱香, 傅彦.加速增长的HK网络演化模型[J]. 计算机科学, 2015, 42(4): 37-39.(CUI A X, FU Y. HK network evolution model with accelerated growth [J]. Computer Science, 2015, 42(4): 37-39.)

[12] ZHAO Y. Public opinion evolution based on complex networks [J]. Cybernetics and Information Technologies, 2015, 15(1): 55-68.

[13] 吴云, 张伟, 宋华.在线舆论演化模型与动力学分析[J]. 武汉理工大学学报(信息与管理工程版), 2016, 38(3): 285-288.(WU Y, ZHANG W, SONG H. Evolution model and dynamics analysis of online public opinion [J]. Journal of Wuhan University of Technology (Information and Management Engineering), 2016, 38(3): 285-288.)

[14] ALBI G, PARESCHI L, ZANELLA M. Opinion dynamics over complex networks: kinetic modelling and numerical methods [EB/OL]. [2017- 03- 22]. https: //arxiv.org/abs/1604.00421.

[16] ALVAREZ-MARTNEZAE R, COCHOBE G, RODRGUEZ R F. Birth and death master equation for the evolution of complex networks [J]. Physica A: Statistical Mechanics and its Applications, 2014, 402(10): 198-208.

[17] FURIOLI G, PULVIRENTI A, TERRANEO E. Fokker-Planck equations in the modeling of socio-economic phenomena [J]. Mathematical Models and Methods in Applied Sciences, 2016, 27(1): 115-158.

This work is partially supported by the National Natural Science Foundation of China (61100008), the Natural Science Foundation of Heilongjiang Province of China (LC2016024).