特征点标注与聚类的三维模型信息隐藏算法
任 帅,张 弢,徐振超,王 震,贺 媛,柳雨农
(1.长安大学 信息工程学院,西安 710064; 2.长安大学 电子与控制工程学院, 西安 710064)(*通信作者电子邮箱maxwellren@qq.com)
0 引言
信息隐藏技术以秘密信息传输的“存在级”安全成为网络空间安全领域中应用的热点。在近几年的三维模型信息隐藏算法中,文献[1]利用骨架对三维模型进行欧氏内切球解析,以最小内切球解析次数为修改变量实现信息隐藏;文献[2-3]利用三维模型外部轮廓数据对三维模型进行解析与修改;文献[4]通过设计等高线空间分割和帧化采样,应用小波域马尔可夫模型实现小波系数零树结构的信息隐藏;文献[5]通过修改三维模型立体分区中法向量变化较大点的小波变换系数进行信息隐藏;文献[6]通过结合网格细分,把具有仿射变换不变性的Nielson范数和三角网格的数据表示冗余相结合实现信息隐藏。目前,信息隐藏技术领域的研究重点是对抗联合攻击。联合攻击是指同时利用多种方法对信息隐藏载体进行叠加处理以达到破坏隐藏信息的目的。上述三维信息隐藏算法虽然在对抗攻击的种类、容量性和鲁棒性方面较早期算法有了明显的提高,但由于信息隐藏修改点的解析仅单独利用结构空间或频域参数,没有将两种处理手段联合应用以同时发挥其应用优势,故无法有效抵抗联合攻击;并且上述算法在进行三维模型载体准备阶段,均没有对隐藏变量进行全局性的性能标记,信息嵌入区域均属于局部特征输出变量,制约了信息隐藏算法的普适性能。
本文在此基础上提出一种基于特征点标注与聚类的隐藏算法。该算法综合利用边折叠网格简化、局部高度理论以及Mean Shift聚类分析算法对三维载体模型数据顶点进行标注与能量划分。边折叠网格简化旨在进行全局能量特征标注以及容量控制;局部高度理论则侧重于进行局部能量标注;而Mean Shift聚类则是为了达到按照能量进行区域划分的目的。本文算法将在特定能量顶点集合中隐藏相应信息,消除不可见性与鲁棒性的冲突问题,达到既能减少信息隐藏嵌入对三维模型的表征影响,又能进一步增强对抗各类单一攻击和联合攻击的鲁棒性能的目的。
1 本文信息隐藏算法
本文提出的信息隐藏算法主要分为四个阶段:首先是基于边折叠网格简化,这里的“简化”并非真实删除,而是依照简化过程中的淘汰顺序进行三维模型全部顶点的标注,即按照重要程度进行排序;其次,参照边折叠网格简化的排序顺序,提取一定区间段的三维模型顶点组成“过程简化模型”,并利用局部高度理论对“过程简化模型”中的顶点进行局部高度标注;再次,利用Mean Shift理论对已经标注局部高度的顶点进行进行聚类,生成修改点;最后,对隐藏信息和载体信息进行优化匹配与修改,实现信息的最终隐藏。
1.1 边折叠网格简化的标注与筛检
三维模型在计算机中的表示由顶点和三角面片组合而成。通常原始三维数据模型数据量大,细节也最为清楚。边折叠网格简化技术则是在保持原有几何形状特征不变的前提下减少模型数据量[7],原理如图1所示。选定图1(a)有向边e以及所连接顶点u和v,将其中较不重要的顶点u“合并”至顶点v,修改网格拓扑关系后三角形f1和f2被删除,生成的网格简化如图1(b)所示。

图1 边折叠网格简化示意图
边折叠删除顶点和边是依据边折叠代价最小原则,即每次删除两顶点欧氏距离与起点重要度乘积最小的边。顶点(起点)重要度定义如式(1)所示:
(1)
有向边euv(起点为u,终点为v)的边折叠代价如式(2)所示:
Ceuv=‖v-u‖·λu
(2)
其中:T(u)为包含顶点u的三角面片集合;T(uv)为同时包含顶点u和v的三角面片集合;Ntn为三角面片tn的面法线长度;Nfn为三角面片fn的面法线长度;‖v-u‖为u、v顶点的欧氏距离。
由于基于边折叠代价最小的网格简化过程,始终删除当前代价最小的边和顶点,使得三维模型最大限度地保持原有外部轮廓和内部细节特征。通过边折叠网格简化对三维模型进行解析的过程就是识别每个顶点对整个三维模型重要程度的过程。重要程度在信息隐藏技术中被视作能量,与不可见性成反比,但与鲁棒性成正比,即越难以隐藏,嵌入的信息鲁棒性也会更好。例如,通过对图2(a)所示的包含11 105个顶点的原始模型进行筛选简化,得出由1 737个顶点构成的简化模型(图2(b))。简化模型仍然可以表达出原始三维模型的主体信息,故筛选后保留的1 737个顶点具有较高的鲁棒性。简言之,边折叠网格简化在整个算法中的作用就是进行三维模型顶点的重要度标注与排序,完成一级信息隐藏区域的筛检。

图2 三维模型网格简化示例
1.2 局部高度的标注与筛检
“局部高度”是一种三维模型的显著性度量方式[8],设顶点v的R-邻居点集合为NR(v),则顶点v的局部高度计算公式为:

(3)
其中:C为NR(v)中顶点所关联面片的面积和;h(v,v′)为曲面上v点与v′之间的相对高度;S(x)为符号函数,当x>0时S(x)为1,否则为0。
本文算法利用局部高度理论,对经过边折叠网格简化步骤后已标注和排序的模型顶点进行局部高度计算,进行按照载体能量和结构特性衡量顶点的二次标注与筛检。与边折叠网格简化时进行的全局顶点标注排序不同的是,局部高度的测量范围仅为单个顶点所联面片的局部范围,使得本文算法标注与筛检处理的过程符合从整体到局部依次进行。
1.3 Mean Shift聚类
Mean Shift是一种非参数化的概率密度估计方法[9],定义Sh(x)是中心位于顶点x(x={x1,x2,…,xn}),半径为h的超球面,包含nx个数据顶点。Mean Shift向量如式(4)所示:
(4)
对于给定|Mh(x)|的阈值t,通过对样本集中的数据点,按x←x+Mh(x)反复迭代收敛x到概率密度函数的局部极大值或局部极小值,完成Mean Shift聚类。
本文利用其对经过边折叠和局部高度双重筛检后的标识顶点进行聚类分析,划分出最终的载体特征顶点集合,此集合称为基于能量划分特性的信息隐藏嵌入区域。嵌入区域重要与非重要的区别提取,符合人类观察物体主次有别的视觉系统规律,符合信息隐藏技术中隐藏区域能量和视觉特性。
1.4 隐藏信息的详细嵌入步骤
基于特征点标注与聚类的三维模型信息隐藏算法的核心思路是联合边折叠网格简化、局部高度以及Mean Shift聚类分析三种方法,将三维载体的全部顶点进行能量标注,筛检出适合隐藏信息的能量权重区域;使用混沌映射和遗传优化算法将欲隐藏信息和载体自身信息进行最大一致化统一,以减少对载体修改为目,提高信息隐藏应用性能;设计鲁棒性区域和脆弱性区域并嵌入对比信息,使得本文算法对是否遭受攻击有较为敏锐的判断。本文算法包含以下11个步骤。
步骤1 读取三维模型.off文件,获取其几何信息,其中顶点数量记作N。
步骤2 遍历所有顶点,按照式(1)~(2)计算全局边折叠代价,并按代价的升序对所有点进行标注排序,记作Pn(n∈[1,N])。


步骤5 选取步骤2中排序的后q个点“组成”的三维模型进行局部高度标注和Mean Shift聚类。将此q个顶点分为局部极大值点集合(记作L"max)、局部极小值点集合(记作L"min)和普通点集合(记作L"gen)。此时的局部极大值点集合L"max和局部极小值点集合L"min统称为“鲁棒点”,记作L"fv,普通点L"gen称为“亚鲁棒点”。
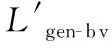
步骤7 根据隐藏信息的总比特数和模型顶点总数确定0/1序列中用于隐藏的比特位数。利用Logistic混沌映射置乱隐藏信息,如式(5)所示:
gk+1=μgk(1-gk);gk∈(0,1)
(5)


(6)
其中:0≤F(i)≤s,s为最终解析出的亚鲁棒点L"gen个数的48倍。
利用遗传算法优化求解,得出最优解i。本步骤利用遗传优化算法的条件逼近,让欲隐藏的信息和载体本身所含的信息最大一致化,最大限度减少对载体的修改,从根本上提高信息隐藏应用的性能。

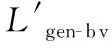
步骤11 将隐藏信息后的三维模型载体顶点坐标值转化为十进制,恢复整个三维模型,生成三维模型含密载体。
2 实验与结果分析
利用Matlab实现了本文算法,使用Bunny、Camel和Rabbit模型进行仿真。Bunny模型有34 268个顶点,Camel模型有38 965个顶点,Rabbit有35 297个顶点。本文算法中参数的取值如下:R=5,t=0.05,p=500,q取模型全部顶点数量的80%。图3为原始三维模型载体,图4为嵌入隐藏信息后的三维模型。
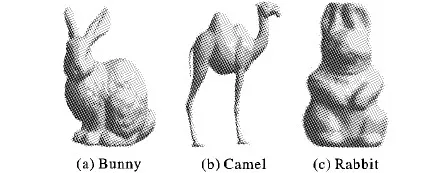
图3 原始三维模型

图4 嵌入信息后的三维模型
2.1 不可见性
峰值信噪比(Peak Signal-to-Noise Ratio, PSNR)[10]和Hausdorff距离[11]是简单有效的测量3D模型修改的方法,可判断算法的不可见性,实验结果如表1所示。

表1 本文算法的峰值信噪比和Hausdorff距离
实验结果表明,本文的信息隐藏算法对模型修改较小。具体应用可根据要求通过降低信息隐藏量获得更高的不可见性。
2.2 鲁棒性
对隐藏信息后的三维模型进行噪声、非均匀简化、平滑、旋转、非均匀缩放、顶点重排序以及联合攻击。实验结果利用提取信息比特序列{sn′}和原始信息序列{sn}的相关系数给出,相关系数记作Corr,如式(7)所示:
(7)
其中:Corr∈[0,1]。Corr=1表示相关性最大,即提取出的信息与原始信息完全一致,表明鲁棒性最强;Corr=0表示无相关性,即信息遭受全部的破坏,鲁棒性最弱。
进行噪声攻击,给三维载体中每个特征顶点加入一个平均分布的随机噪声矢量,顶点到三维载体几何中心的平均距离取0.5%、1.0%、1.5%和2.0%,实验结果取三次噪声攻击的平均值,如表2所示。当噪声强度为1.0%时,载体表面的细节部分破坏严重,但噪声强度增加到2.0%时,仍然可以从载体中解析出较识别的隐藏信息,说明算法对随机噪声有较强的鲁棒性。

表2 噪声攻击实验的相关系数
进行非均匀简化攻击,将三维载体的顶点分别简化20%、35%、50%和65%,实验结果如表3所示。简化程度接近65%时,解析出的信息仍可以有效识别,表明所提算法对非均匀简化攻击具有较强的抵抗性。
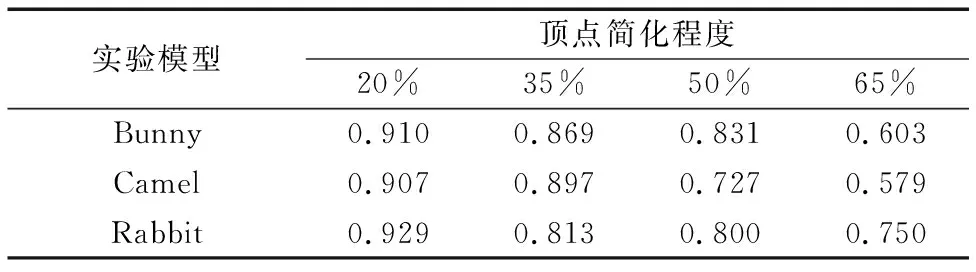
表3 非均匀简化攻击实验的相关系数
进行Laplacian平滑攻击,实验设置迭代的次数为15、25和35,实验结果如表4所示。在进行35次迭代后,三维载体的表面严重破坏,但仍然可以提取识别度较高的隐藏信息,说明算法对Laplacian平滑攻击有较强的鲁棒性。

表4 平滑攻击实验的相关系数
进行旋转攻击,轴旋转角度记作(x,y,z),实验数据如表5所示。算法面对旋转攻击,性能处在50%的相关度,但依旧可以进行有效识别,具有一定强度的鲁棒性能。

表5 旋转攻击实验的相关系数
在对三维模型的常规攻击中,也包含非均匀缩放攻击和顶点重排序攻击[12],本文算法对抗非均匀缩放攻击和顶点重排序攻击的可视化实验结果在图5中连同噪声、非均匀简化、平滑、旋转一并给出,可以看出基于本文算法的含密模型在受到攻击后提取出的信息具有良好的视觉效果。
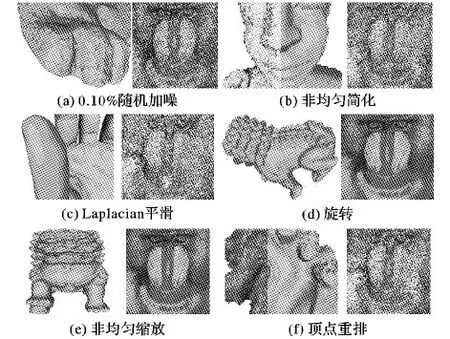
图5 六种常见攻击的信息可视化提取效果
不同类型和典型强度组合的联合攻击实验结果如表6所示。三维载体模型经过联合攻击后,提取出的隐藏信息与原始信息耦合系数仍然在50%分位,且实际的可识别情况效果更好,表明所提算法对联合攻击具有较强的鲁棒性。
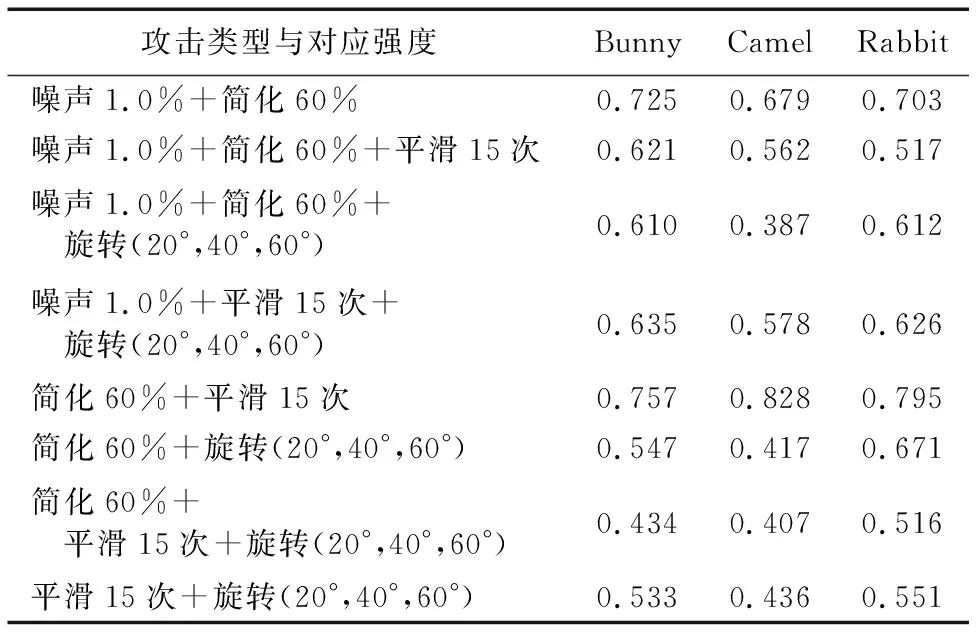
表6 联合攻击实验的相关系数
从实验结果可以看出,本文算法对单独的噪声、非均匀简化、平滑、旋转、非均匀缩放、顶点重排序以及由其组合的攻击进行实验。当噪声强度达到3%、非均匀简化达到85%、平滑达到35次,以及经过各种联合攻击时,三维载体模型的表面细节严重破坏,但仍然可以提取出相关程度较高的信息,解析信息仍然满足可视化识别的要求。对不同类型的非均匀缩放攻击和顶点重排序攻击,尽管三维模型新的顶点大幅偏移,但提取出的信息仍然可以有效识别,表明本文算法对非均匀缩放和顶点重排这类破坏性更强的攻击仍然具有较强的鲁棒性。综上所述,本文算法在满足不可见性的首要要求下,可以抵御常见攻击及其联合攻击,为秘密信息通信提供可靠的技术支持。
2.3 算法比较
将本文算法与文献[1-2]算法进行性能比较,因为这三种算法都是利用能量解析与区域划分进行的盲信息隐藏的算法设计,且文献[1-2]算法性能较早前类似算法具有一定的性能优势。文献[1]将骨架最为能量权重衡量基点,通过修改圆环解析数量进行信息隐藏;文献[2]是本文前期的工作,通过进对模型纵向轮廓Z轴值的区间解析实现信息隐藏,Z轴解析过程中同样使用了Mean Shift进行轮廓曲线的局部聚类。本文算法在相同不可见性的前提下,利用Bunny、Camel、Rabbit模型进行实验,对嵌入信息后的三维模型进行攻击,然后进行信息提取检测比较算法的鲁棒性。实验结果以相关系数给出,如表7所示。

表7 三种算法实验的相关系数比较
从表7可以看出,本文算法对旋转攻击和剪切攻击的鲁棒性弱,但其他类型的单独或联合攻击的鲁棒性均强于其他两种算法。原因在于需要将隐藏信息重复嵌入的三维空间以获得多个冗余副本,而本文算法在边折叠和局部高度划分区域时无法做到空间位置的重复性选取,因此对抗旋转攻击和剪切攻击的性能弱于其他两种算法。但从实验的可视化结果可知,当模型旋转纬度达到60°时,本文算法依然能提取出人眼可以识别出的有效信息,在极端条件下算法仍然具有应用价值实际。通过比较可知,根据三维模型顶点能量权重安排的信息隐藏策略性嵌入,能够提高信息隐藏的算法性能。
3 结语
本文基于能量解析思想,利用边折叠网格简化技术和局部高度理论,从全局到局部对三维模型进行能量解析,再利用Mean Shift聚类技术按照能量标记进行区域划分,满足信息隐藏技术的性能要求。由于边折叠网格简化只是进行标记,所以算法中用于隐藏信息的替换顶点可根据所隐藏信息量动态扩展。而鲁棒点与脆弱点的区域划分与信息嵌入设计,可以使信息接收者快速判断是否遭受攻击。本文算法在进行区域生成的过程中,负责全局筛检的边折叠网格简化无法有意设计冗余区域,对抗旋转攻击的性能无法控制。下一步将研究面向冗余空间设计的边折叠网格简化技术,以增强本文算法在对抗旋转和剪切攻击的鲁棒性。
参考文献(References)
[1] 张弢, 慕德俊, 任帅, 等. 利用内切球解析的三维模型信息隐藏算法[J]. 西安电子科技大学学报(自然科学版), 2014, 41(2): 185-190.(ZHANG T, MU D J, REN S, et al. Information hiding scheme for 3D models based on skeleton and inscribed sphere analysis[J]. Journal of Xidian University, 2014, 41(2): 185-190.)
[2] 任帅, 石方夏, 张弢. 基于三维模型轮廓解析的信息隐藏算法[J]. 计算机应用, 2016, 36(3): 642-646.(REN S, SHI F X, ZHANG T. Research on information hiding scheme for 3D models based on profile analysis [J]. Journal of Computer Application, 2016, 36(3): 642-646.)
[3] 雷敬祥. 基于能量权重的信息隐写算法设计与研究[D]. 西安: 长安大学, 2016: 39-48.(LEI J X. Design and research of information steganography algorithm based on energy weight [D]. Xi’an: Chang’an University, 2016: 39-48.)
[4] 綦科, 张大方, 谢冬青. 基于帧化采样和小波HMM的三维模型信息隐藏[J]. 计算机辅助设计与图形学学报, 2010, 22(8): 1406-1411.(QI K, ZHANG D F, XIE D Q. Steganography for 3D model based on frame transform and HMM model in wavelet domain [J]. Journal of Computer-Aided Design & Computer Graphics, 2010, 22(8): 1406-1411.)
[5] 任帅, 张弢, 杨涛, 等. 基于三维模型球型分割的信息隐藏算法[J]. 计算机应用, 2017, 37(9): 2581-2584.(REN S, ZHANG T, YANG T, et al. Information hiding algorithm based on spherical segmentation of 3D model [J]. Journal of Computer Application, 2017, 37(9): 2581-2584.)
[6] 黄祥, 谢强. 基于细分曲面的抗仿射变换三维模型数字水印算法[C]// 中国通信学会第六届学术年会论文集. 深圳: 国防工业出版社, 2013: 144-147.(HUANG X, XIE Q. A blind and affine invariant 3D mesh watermark based on mesh subdivison[C]// Proceedings of the 6th Annual Academic Conference of the China Communications Association. Shenzhen: National Defense Lndustry Press, 2013: 144-147.)
[7] 华顺刚, 钟庆, 李绍帅. 基于边折叠网格简化的三维形状变形[J]. 大连理工大学学报, 2011, 51(3): 363-367.(HUA S G, ZHONG Q, LI S S. 3D shape deformation based on edge collapse mesh simplification[J]. Journal of Dalian University of Technology, 2011, 51(3): 363-367.)
[8] 林金杰, 朱代辉, 杨育彬, 等. 3维模型局部高度研究[J]. 中国图象图形学报, 2011, 16(10): 1841-1849.(LI J J, ZHU D H, YANG Y B, et al. Three-dimensional model study on local height [J]. Journal of Image and Graphics, 2011, 16(10): 1841-1849.)
[9] PIPAUD I, LEHMKUHL F. Object-based delineation and classification of alluvial fans by application of mean-shift segmentation and support vector machines[J]. Geomorphology, 2017, 293: 178-200.
[10] 王新宇, 詹永照. 构造顶点分布特征的三维模型数字水印算法[J]. 计算机辅助设计与图形学学报, 2014, 26(2): 272-279.(WANG X Y, ZHAN Y Z. A watermarking scheme for three-dimensional models by constructing vertex distribution on characteristics [J]. Journal of Computer-Aided Design & Computer Graphics, 2014, 26(2): 272-279.)
[11] CARLSON N A, PORTER J R. On the cardinality of Hausdorff spaces and H-closed spaces[J]. Topology & its Applications, 2017, 160(1): 137-142.
[12] 吴建国, 邵婷, 刘政怡. 融合显著深度特征的RGB-D图像显著目标检测[J]. 电子与信息学报, 2017, 39(9): 2148-2154.(WU J G, SHAO T, LIU Z Y. RGB-D saliency detection based on integration feature of color and depth saliency map [J]. Journal of Electronics & Information Technology, 2017, 39(9): 2148-2154.)
This work is partially supported by the National Natural Science Foundation of China (61702050, 61402052), the National Innovation and Entrepreneurship Training Program for College Students (201610710036).

