基于统计模量和局部近邻标准化的局部离群因子故障检测方法

冯立伟,张 成,李 元,谢彦红

(1.沈阳化工大学 数理系,沈阳 110142; 2.沈阳化工大学 过程故障诊断研究中心,沈阳 110142)(*通信作者电子邮箱li-yuan@mail.tsinghua.edu.cn)

0 引言

主元分析(Principal Component Analysis, PCA)、偏最小二乘方法(Partial Least Square, PLS)和独立元分析(Independent Component Analysis, ICA)是经典的故障检测方法,在工业过程中已经得到广泛应用[1-8]，它们都假定数据来自单一工况，但现在工业生产广泛采用多工况生产过程。多工况过程数据具有多中心[9-12]、各工况分布结构不同[13-14]、各批次数据为矩阵形式且批次不等长[11-12,15]等特点。由于数据具有多中心的特点,因此数据不服从单一多元高斯分布,而PCA、PLS方法中的统计量要求数据服从多元高斯分布, ICA方法要求数据服从单一分布,这导致PCA、PLS、ICA方法在多工况故障检测过程中出现严重误报和漏报。

针对多工况过程的多中心特征,出现了高斯混合模型(Gaussian Mixture Model, GMM)[9-10],首先对每个工况使用PCA、PLS、ICA等方法构造检测子模型,再使用贝叶斯推理来综合各模型检测结果。张成等[16]提出基于GMM的马氏距离k近邻(k-Nearest Neighbor, kNN)故障检测。但GMM的子模型个数事先未知,在复杂工业过程中难于应用。如何对多工况过程建立单一检测模型成为研究重点。He等[17]提出了k近邻的故障检测(Fault Detection using kNN rule, FD-kNN)方法,并应用在半导体蚀刻工艺过程中,成功检测出大多数故障。FD-kNN方法通过使用累计距离统计指标度量样本间的相似度,能够有效降低多中心的影响,提高过程故障检测率。此外,处理多中心问题的方法还有局部离群因子(Local Outlier Factor, LOF)方法。马贺贺等[13]提出基于局部邻域密度的马氏距离局部离群因子的故障检测方法。刘帮莉等[14]提出基于局部密度估计的多工况故障检测方法。局部离群因子是一种对样本基于局部密度的离群程度的度量。故障样本相对于正常样本集是离群点,所以局部离群因子可以用来区分故障样本和正常样本,从而可以实现故障检测。但是当各工况分布结构差异明显时,FD-kNN和LOF的检测性能明显降低。

针对多工况数据中各个工况分布结构差异明显的困难,Ma等[18]提出基于局部近邻标准化(Local Neighborhood Standardization, LNS)的局部离群因子故障检测方法,并应用于TE(Tennessee Eastman)过程中。Ma等[19]提出基于局部近邻标准化策略的故障检测方法,也应用于TE过程中。局部近邻标准化能够将工况结构差异明显的多工况数据融合为单一工况数据。

此外,很多工业过程数据为矩阵形式且批次不等长,无法直接进行故障检测,在检测之前需将矩阵数据转化成向量形式,文献[11]中对半导体生产数据按时间方向展开为向量形式,针对批次不等长的特征,只截取了一部分数据。Wang等[11,15]提出统计模量分析(Statistics Pattern Analysis, SPA)的数据处理方法,用数据变量的统计模量来代替原始数据。张成等[12]将统计模量分析方法应用于间歇过程中。建立在统计模量分析基础上的故障检测方法能够提取过程数据的主要信息,将矩阵形式样本转化为向量形式样本,同时克服批次不等长的影响,提高故障检测效率。

针对多工况过程数据的上述特征,本文提出一种在数据的统计模量基础上使用局部近邻标准化和局部离群因子的故障检测方法——SP-LNS-LOF。首先计算每一个样本的统计模量,其次使用局部近邻集标准化统计模量,最后计算标准样本的局部离群因子,当在线样本的局部离群因子大于由训练集的局部离群因子所确定的控制限时,判定当前样本为故障;否则为正常。

1 统计模量分析

工业过程数据通常是三维矩阵形式X(I×J×K)，如半导体蚀刻过程数据,I为间歇操作次数,J为过程变量个数,K为采样时刻数。由于每一批次数据都是矩阵形式,在检测之前需要预处理为向量形式,经典预处理方法是多向方法。记第i个批次的数据为xi,xi为图1(a)中的一层数据。

(1)

多向方法将矩阵样本xi按时间方向展开为向量:

使用多向方法展开后变量数变为JK,当采样时刻较多时,JK会非常大,给后续故障检测方法带来负担；并且多向方法只能处理等长数据(采样时刻数K相等),对不等长数据需从中截取等长数据再进行检测。

统计模量分析通过计算样本变量的各阶统计模量来代替样本本身。常用的统计量有变量均值μij、方差σij、偏度γij、峰度κij等。

均值和方差表征了变量的中心和分散程度,偏度和峰度表征了变量分布的偏斜程度和陡峭程度。对于样本xi计算其各阶统计模量组成统计模量向量:

si=[μi1,μi2,…,μim,σi1,σi2,…,σim,γi1,γi2,…,

γim,κi1,κi12,…,κim]

(2)

使用si替换样本xi进行故障检测。统计模量si提取了数据的主要信息,降低了数据维度,同时克服了批次不等长的困难,能够为后期的故障检测提供良好的数据基础。

图1给出使用SPA进行故障检测的两个基本步骤:

Step1 通过计算各批次变量的统计模量提取批次过程的分布特征,将矩阵形式样本转化为向量形式,如图1(a)、(b)。

Step2 使用故障检测方法计算正常批次统计模量样本的检测指标,确定控制限,进行故障检测,如图1(c)。

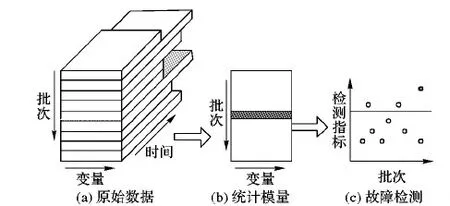
图1 SPA故障检测

2 局部近邻标准化

因为数据变量的量纲通常不相同,在进行故障检测之前数据需标准化。经典的标准化方法是zscore方法。使用zscore方法处理多工况数据,只能消除变量的量纲,不能消除数据的多工况特征。另一种标准化方法是局部近邻标准化。

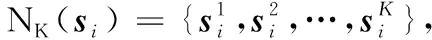
(3)

(4)

(5)

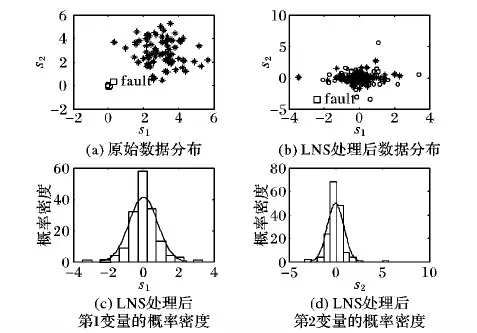
图2 局部近邻标准化

下面使用例子说明LNS的作用,正常样本集由含两个变量的两个工况数据组成：工况1的两个变量都服从均值为0、标准差为0.05的高斯分布；工况2的两个变量都服从均值为3、标准差为1的高斯分布,共有80个样本,设定故障点fault(0.3,0.3)。如图2(a)所示,原始正常数据明显分为两个工况,且两个工况的数据离散程度差异明显。使用LNS方法对图2中数据进行标准化,近邻参数K为10,得到的结果如图2(b),两个变量的概率密度见图2(c)～(d)。此时LNS方法能够将两个工况数据聚合为工况分散程度近似相同的单一工况,且故障点偏离正常数据集。

3 局部离群因子方法

Breunig等[20]提出一种基于局部离群因子(LOF)的离群点检测方法，LOF方法使用局部离群因子度量样本点的离群程度。

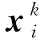
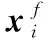
(6)

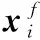
3)样本xi的局部可达密度:

(7)

表示xi的第k邻域集Nk(xi)内样本到xi的平均可达距离的倒数。

4)样本xi的局部离群因子:

(8)

表示xi的邻域集Nk(xi)中样本的局部可达密度与xi的局部可达密度之比的平均数。

LOF方法使用样本所在局部邻域集的样本相对密度来度量样本的离群程度。正常样本周围的正常样本较多,因此密度较大,则其局部离群因子较小;而故障样本离正常样本较远,因此其周围正常样本密度较小,则其局部离群因子较大。

4 SP-LNS-LOF方法

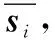
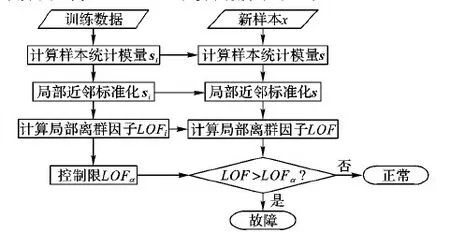
图3 SP-LNS-LOF算法流程

4.1 离线建模

1)根据式(2)计算训练样本集中每个样本xi的各阶统计模量,组成统计模量向量si,得到新训练集S。

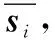
4.2 在线检测

1)根据式(2)计算新样本x的各阶统计模量,组成统计模量向量s。

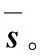
3)根据式(8)计算x的局部离群因子LOFx。

4)若LOFx>LOFα,则判定样本x为故障样本；否则为正常样本。

统计模量向量si提取了数据的主要信息,将每一个矩阵形式数据转化为向量形式,简化了数据量,并且克服了数据批次不等长的困难;局部近邻标准化将工况方差不同的多工况数据融合为单一工况;局部离群因子度量了样本间的相似程度,表征了故障样本和正常样本的差异。

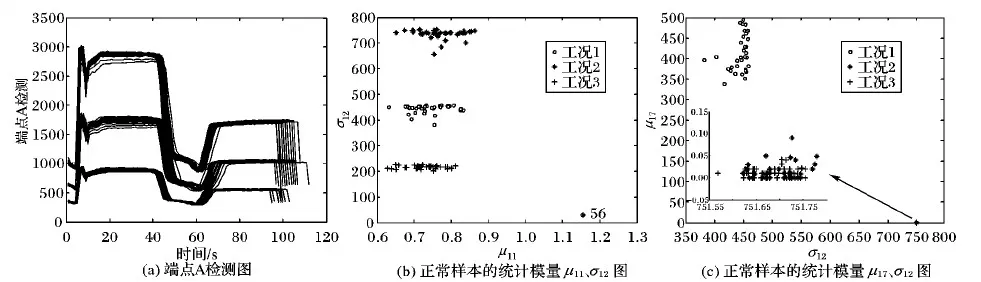
图4 半导体数据图

5 半导体生产过程故障检测实例

数据采自半导体生产中铝蚀刻工艺过程[21-22],共有来自三组实验的129个批次晶片数据:108个正常晶片数据,其中第56个批次数据部分缺失;21个故障晶片数据,其中第12个批次缺失。按文献[21]选取19个检测变量,见表1。故障样本是在表2所列变量上人为增加或减少相应幅度值进行实际实验得到的,详细描述见文献[21]。半导体数据被广泛应用于检验故障检测算法的性能,如文献[11-12,16-17]。

图4(a)为所有正常样本的端点A检测图像,可看出正常样本分为三个工况且批次长度不同。图4(b)为所有正常样本的统计模量向量的两个变量μ11、σ12的图像,数据仍然分为三个工况,其中第56个批次样本缺失部分数据。图4(c)为变量μ17、σ12的图像,工况1比较稀疏,工况2、3比较密集,即各工况疏密程度不同。

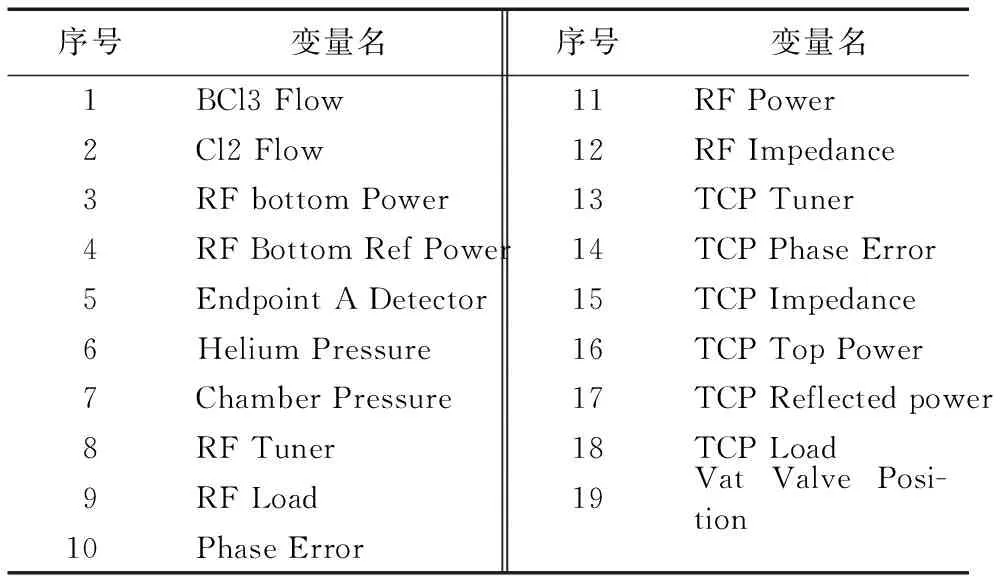
表1 过程变量

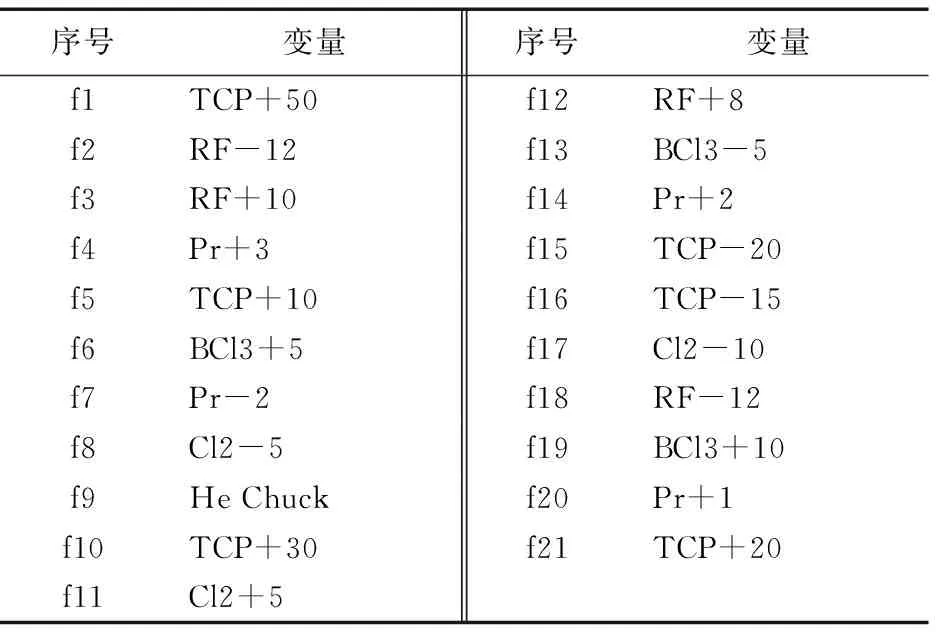
表2 故障类型

本文采用对每一批次的矩阵数据计算变量均值和方差的方法组成统计模量向量。

在正常样本中随机选择第12、23、40、45、48、60、 96、104批次作为校验数据,其余为训练数据,使用SP-LNS-LOF方法与PCA、核主元分析(kernel PCA, kPCA)、FD-kNN、LOF方法对21个故障过程数据进行故障检测和对比分析。仿真实验过程中所有方法的置信度α=97%。仿真实验结果见图5和表3。

PCA按95%的累计贡献率取主元个数为20,检测结果见图5(a)～(b),T2有10个故障未检出,平方预报误差(Squared Prediction Error, SPE)检出全部21个故障但有3个正常样本的误报。多工况样本集不满足PCA中统计量T2和SPE对数据的多元高斯分布的假设。kPCA中采用高斯径向核函数,其中的核参数取为1 000,仍按95%累计贡献率取核主元个数为23,检测结果见图5(c)～(d),kPCA的T2有11个故障未检出,SPE有1个故障未能检测出,且有3个正常样本的误报,这仍然是数据的多工况特征造成的。kNN方法近邻数k=4,检测结果见图5(e),有7个故障未能检测出,未能检测出的原因在于各工况中样本的疏密程度不同,见图4(c)。SP-zscore-LOF方法中近邻参数K=10,检测结果见图5(f),有6个故障未能检测出,原因仍为各工况疏密程度不同。

表3 故障检测结果

图5 故障检测结果

SP-LNS-LOF方法中参数K=10,k=4,检测结果见图5(g),检测出全部21个故障且误报为0。LNS处理能够使各个工况疏密程度近似相等,使LOF能够在同一尺度上计算相对密度,从而实现故障样本和正常样本的分离。

6 结语

本文针对多工况过程数据特征,提出了基于统计模量的局部近邻标准化局部离群因子故障检测方法。通过在统计模量样本集上联合使用局部近邻标准化和局部离群因子克服过程数据批次不等长、工况中心漂移和工况结构差异明显的困难,提高多工况过程的故障检测率。对半导体蚀刻过程数据的故障检测实验,验证了方法的有效性。

参考文献(References)

[1] GE Z, SONG Z. Semiconductor manufacturing process monitoring based on adaptive substatistical PCA[J]. IEEE Transactions on Semiconductor Manufacturing, 2010, 23(1): 99-108.

[2] CHERRY G A, QIN S J. Multiblock principal component analysis based on a combined index for semiconductor fault detection and diagnosis[J]. IEEE Transactions on Semiconductor Manufacturing, 2006, 19(2): 159-172.

[3] GE Z, YANG C, SONG Z. Improved kernel PCA-based monitoring approach for nonlinear processes[J]. Chemical Engineering Science, 2009, 64(9): 2245-2255.

[4] ZHANG C, LI Y. Study on the fault-detection method in batch process based on statistical pattern analysis[J]. Chinese Journal of Scientific Instrument, 2013, 34(9): 2103-2110.

[5] SANG W C, LEE C, LEE J M, et al. Fault detection and identification of nonlinear processes based on kernel PCA[J]. Chemometrics & Intelligent Laboratory Systems, 2005, 75(1): 55-67.

[6] ZHANG Y, HU Z. Multivariate process monitoring and analysis based on multi-scale KPLS[J]. Chemical Engineering Research & Design, 2011, 89(12): 2667-2678.

[7] GE Z, SONG Z. Mixture Bayesian regularization method of PPCA for multimode process monitoring[J]. AIChE Journal, 2010, 56(11): 2838-2849.

[8] ZHAO C, YAO Y, GAO F, et al. Statistical analysis and online monitoring for multimode processes with between-mode transitions[J]. Chemical Engineering Science, 2010, 65(22): 5961-5975.

[9] YU J, QIN S J. Multimode process monitoring with Bayesian inference-based finite Gaussian mixture models[J]. AIChE Journal, 2008, 54(7): 1811-1829.

[10] YU J, QIN S J. Multiway Gaussian mixture model based multiphase batch process monitoring[J]. Industrial & Engineering Chemistry Research, 2009, 48(18): 8585-8594.

[11] WANG J, HE Q P. Multivariate statistical process monitoring based on statistics pattern analysis[J]. Industrial & Engineering Chemistry Research, 2010, 49(17): 7858-7869.

[12] 张成,李元. 基于统计模量分析间歇过程故障检测方法研究[J]. 仪器仪表学报, 2013, 34(9): 2103-2110.(ZHANG C, LI Y. Study on the fault-detection method in batch process based on statistical pattern analysis [J]. Chinese Journal of Scientific Instrument, 2013, 34(9): 2103-2110.)

[13] 马贺贺, 胡益, 侍洪波. 基于马氏距离局部离群因子方法的复杂化工过程故障检测[J]. 化工学报, 2013, 64(5): 1674-1682.(MA H H, HU Y, SHI H B. Fault detection of complex chemical processes using Mahalanobis distance-based local outlier factor[J]. CIESC Journal, 2013, 64(5): 1674-1682.)

[14] 刘帮莉, 马玉鑫, 侍洪波. 基于局部密度估计的多模态过程故障检测[J]. 化工学报, 2014, 65(8): 3071-3081.(LIU B L, MA Y X, SHI H B. Multimode process monitoring based on local density estimation[J]. CIESC Journal, 2014, 65(8): 3071-3081.)

[15] HE Q P, WANG J. Statistics pattern analysis: a new process monitoring framework and its application to semiconductor batch processes[J]. AIChE Journal, 2015, 57(1): 107-121.

[16] 张成, 李秀玉, 逄玉俊, 等. 基于GMM的马氏距离kNN故障检测方法[J]. 测控技术, 2014, 33(9): 13-17.(ZHANG C, LI X Y, PANG Y J, et al. Mahalanobis distance kNN fault detection method based on Gaussian mixture model[J]. Messurement & Control Technology, 2014, 33(9): 13-17.)

[17] HE Q P, WANG J. Fault detection using thek-nearest neighbor rule for semiconductor manufacturing processes[J]. IEEE Transactions on Semiconductor Manufacturing, 2007, 20(4): 345-354.

[18] MA H, HU Y, SHI H B. Fault detection and identification based on the neighborhood standardized local outlier factor method[J]. Industrial & Engineering Chemistry Research, 2013, 52(6): 2389-2402.

[19] MA H, HU Y, SHI H B. A novel local neighborhood standardization strategy and its application in fault detection of multimode processes[J]. Chemometrics & Intelligent Laboratory Systems, 2012, 118(7): 287-300.

[20] BREUNIG M M, KRIEGEL H P, NG R T, et al. LOF: identifying density-based local outliers[C]// SIGMOD 2000: Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data. New York: ACM, 2000: 93-104.

[21] WISE B M, GALLAGHER N B, BUTLER S W, et al. A comparison of principal component analysis, multiway principal component analysis, trilinear decomposition and parallel factor analysis for fault detection in a semiconductor etch process[J]. Journal of Chemomotrics, 1999. 13(3): 379-396.

[22] Eigenvector research incorporated. Metal etch data for fault detection evaluation [EB/OL]. [2017- 05- 10]. http: //software.eigenvector.com/Data/Etch/index.html.

This work is partially supported by the National Natural Science Foundation of China (61673279), the Project of Education Department in Liaoning (L2015432), the Natural Science Foundation of Liaoning Province (2015020164).