高分辨率级联电容阵列SARADC可行性分析
中星微人工智能芯片技术有限公司 杨建明 夏昌盛 张韵东
逐次逼近型ADC(SARADC)以其低功耗、高精度在无线通讯、医疗器件、通用信号测量领域获得广泛应用。电容阵列SARADC结构简单,模拟主动器件极少,其内嵌DAC可复用为采样保持电路[1]-[4],面积小功耗低。用于构成电容阵列的半导体电容元件精度有限[5],实际电容阵列SARADC可获得的精度要低于理论精度。本文旨在分析电容匹配误差对电容阵列SARADC精度的影响,推导出补偿电容匹配误差的方法,从而获得高精度SARADC。
1 二进制权值电容阵列
SARADC精度会受内嵌DAC、比较器、基准电压影响。其中DAC的精度是制约SARADC精度的主要因素。本文忽略电路其他因素,只分析SARADC内嵌的电容阵列DAC精度。
1.1 二进制权值电容阵列模型
二进制权值电容阵列如图1所示[6]-[8]。
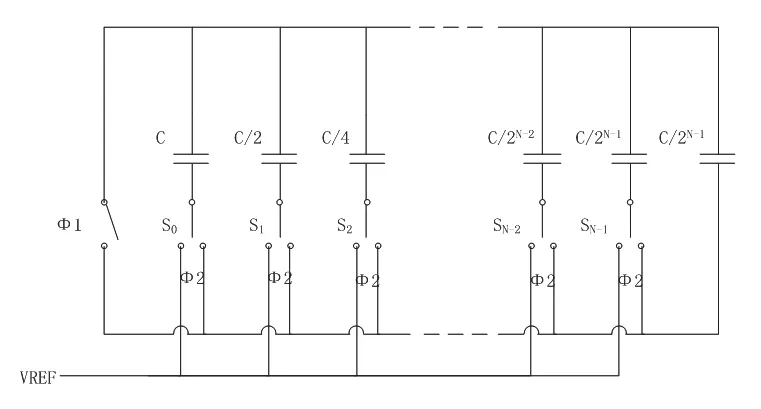
图1 二进制权值电容阵列Fig.1 Binary-weighted Capacitor Array
在Φ1期间,阵列所有电容的两端都接地;Φ2期间,对应位为1的电容与VREF相连,而对应位为0的仍然接地。Φ2期间电容阵列输出有效。
Φ2期间不存在电容阵列充放电路径,从Φ1到Φ2期间电荷守恒。与VREF相连的电容Ceq上的电荷与总电容Ctot中的电荷相等。
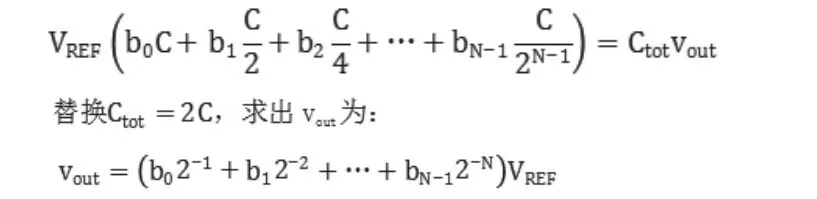
1.2 INL/DNL
由于半导体电容元件存在匹配误差,上式系数会偏离理想值2-i。
在最坏情况假设下推导二进制权值电容阵列的积分非线性和微分非线性。对于一个N位二进制权值电容阵列,当第i个电容只与VREF相连时,理想输出为:
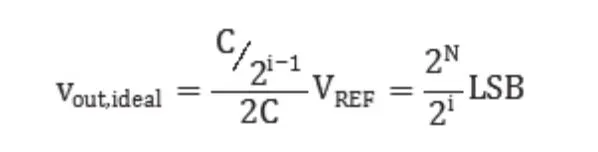
假设电容的容差为,第i个电容在实际的最坏情况下输出为:
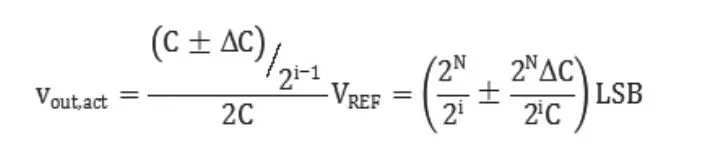
则第i位的INL为:

二进制权值电容阵列的最坏DNL出现在MSB变化时。最坏DNL可表示为:
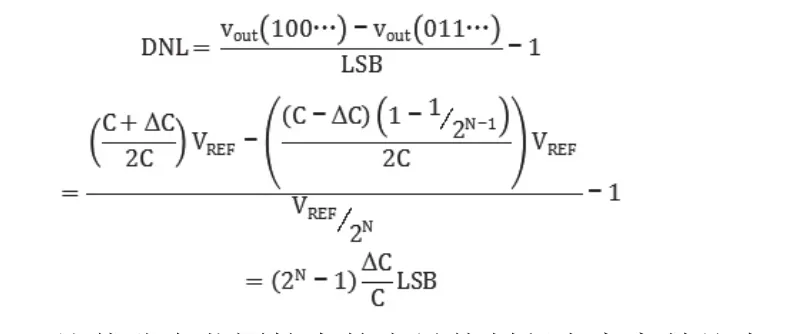
比值分布范围较大的半导体制程电容容差约为。当二进制权值电容阵列为6位时候,DNL约为0.1LSB。
2 容差与匹配
2.1 容差需求
对于一个N位数据转化器,所有位的容差都要小于。第i位的权重因子可以表示为:
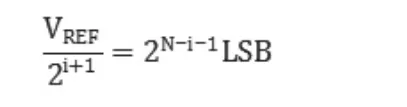
第i位的精度,也就是由权重因子归一化的容差,即为:

2.2 半导体电容匹配特性
图3为TSMC 28nm制程FMOM电容匹配测量数据。
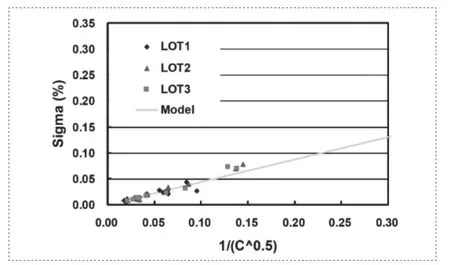
图2 交叉耦合电容匹配误差Fig.2 MX-coupled capacitor mismatch
从图2可知,电容元件的匹配精度随着最大元件与最小元件的比值的增大而降低。考虑到电路功耗面积,最大电容取值存在上限。电容阵列权重因子范围越大,电容间匹配差;相反电容阵列权重因子范围越小,电容间匹配好。
高精度SARADC设计思路可以通过减小电容取值分布范围入手。
3 分割电容阵列
分割电容阵列[12]-[15]通常被用于减小电容阵列取值范围,提升SARADC精度,降低动态切换功耗与面积。分割电容阵列级数选取,以及分割电容本身精度要求却很少有文章推导计算。本文侧重于理论上澄清这些问题。
3.1 分割电容阵列模型
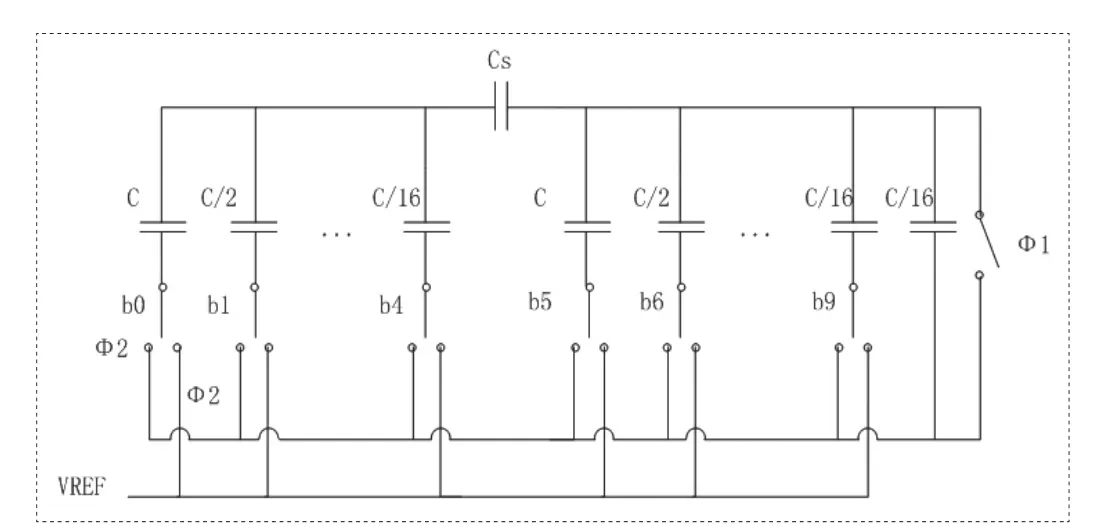
图3 分割电容阵列Fig.3 Split Capacitor Array
基于图2电容匹配数据,16:1电容比值范围内电容匹配误差小于0.1%。采用分割电容阵列(5位MSB,5位LSB)可以获得10bit精度,如图3所示。
分割电容Cs和LSB阵列的串联必须等于MSB阵列的最小权值电容。因此可得:
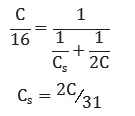
MSB阵列的戴维南等效电压V1和LSB阵列加上终端电容的等效电压V2如下:
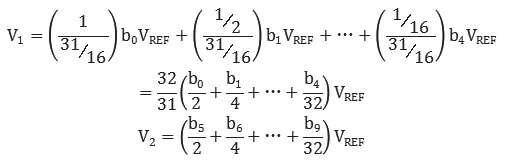
分割电容阵列二端口网络等效电路如图4所示:
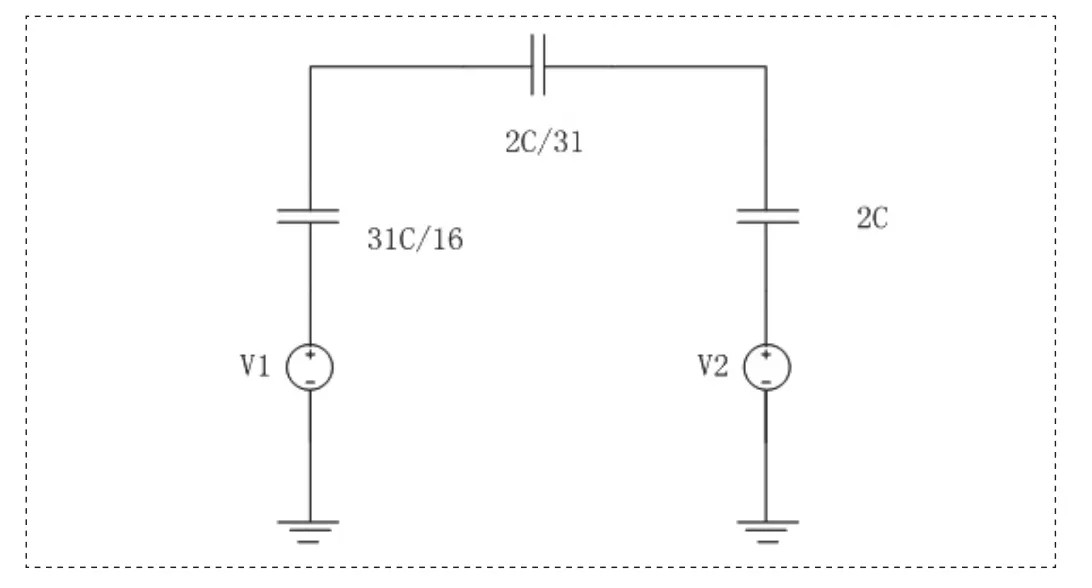
图4 分割电容阵列等效电路Fig.4 Split Capacitor Array Equivalent Circuit
根据此图,理想输出电压为:

3.2 分割电容精度
分割电容与电容阵列单位电容不构成整数比例,实际取值会有取舍。简化计算,假设MSB/LSB电容阵列为理想电容,只考虑分割电容取值误差带来的影响。根据图4,并用泰勒级数展开只保留1次项,输出电压为:
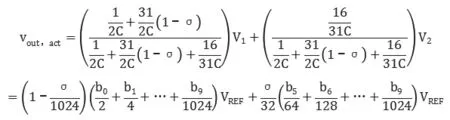
分割电容容差会产生很小的增益误差与LSB阵列权值误差。当LSB位从全零跳变到全1时误差最大,此时对应最坏情况DNL:
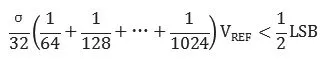
推导出只要满足,最终电容阵列转换精度即可以满足DNL<1/2 LSB。
3.3 级联分割电容阵列
图3所示分割电容阵列可获得10位精度。如果需要更高精度,需要进一步减小电容阵列取值范围,提升电容匹配精度。可以在原分割电容阵列基础上级联分割电容阵列,如图5所示:
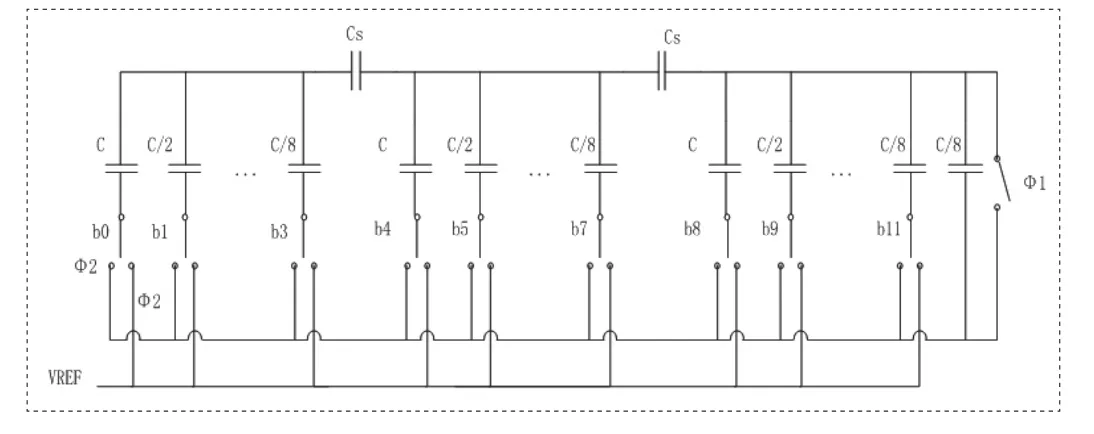
图5 级联分割电容阵列Fig.5 Cascaded Split Capacitor Array
分割电容Cs和LSB阵列的串联必须等于高位电容阵列的最小权值电容。因此可得:
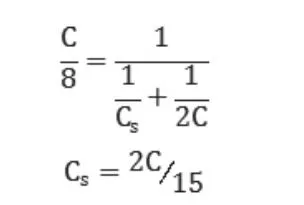
高位阵列的二端口戴维南等效电压V1,2和LSB阵列加上终端电容的等效电压V3如下:
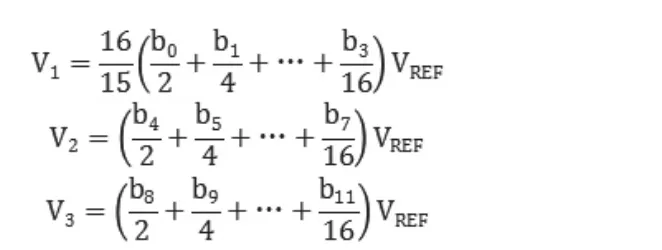
级联分割电容阵列两端口网络等效电路如图6所示:
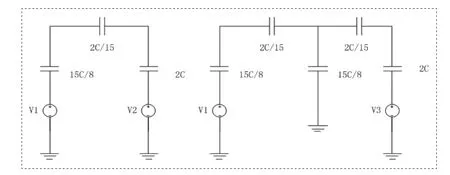
图6 分割电容阵列等效电路Fig.6 Split Capacitor Array Equivalent Circuit
图6 左侧等效电路对应于LSB阵列输入信号全零;右侧等效电路对应于中间级阵列输入信号全零。根据叠加原理,输出信号为:
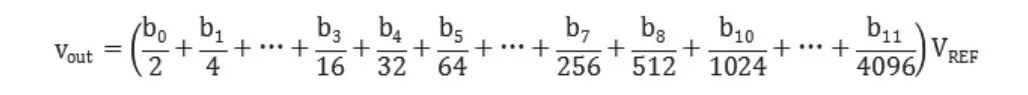
即为12位电容阵列输出电压表达式。
4 验证
本文观点通过Matlab验证了数学模型的可行性,同时基于TSMC28nm制程,通过Spice仿真工具验证12bit SARADC电路,结果与数学模型吻合。
5 结论
本文分析了SARADC核心部件电容阵列DAC等效模型及电容容差对电容阵列精度的影响。提出提升SARADC精度的方法。同时,推导出分割电容自身取值精度要求。本文认为,结合半导体制程电容匹配特性,减小电容阵列电容比值分布范围,提升电容间匹配精度,结合级联分割电容阵列架构,设计上可以获得高精度SARADC。
[1]M.D.Scott,B.E.Boser,and K.S.J.Pister.An ultra low-energy ADC for smart dust[J].IEEE J.Solid-State Circuits,vol.38,no.7,pp.1123-1129,Jul.2003.
[2]N.Verma and A.P.Chandrakasan.An ultra low energy 12-bit rateresolution scalable SAR ADC for wireless sensor node[J].IEEE J.Solid-State Circuits,vol.42,no.6,pp.1196-1205,Jun.2007.
[3]S.Gambini and J.Rabaey.Low-power successive approximation converter with 0.5 supply in 90 nm CMOS[J].IEEE J.Solid-State Circuits,vol.42,no.11,pp.2348-2356,Nov.2007.
[4]J.Sauerbrey,D.Schmitt-Landsiedel,and R.Thewes.A 0.5V 1uW successive approximation ADC[J].IEEE J.Solid-State Circuits,vol.38,no.7,pp.1261-1265,Jul.2003.
[5]P.R.Gray,P.J.Hurst,R.G.Meyer.Analysis and Design of Analog Integrated Circuits[M].John Wiley & Sons,INC.2008
[6]E.Suarez,P.R.Gray,and D.A.Hodges.All-MOS charge redistribution analog-to-digital conversion techniques—Part I[J].IEEE J.Solid-State Circuits,vol.SC-10,no.6,pp.371-379,Dec.1975.
[7]H.Hong and G.Lee.A 65fJ/conversion-step 0.9-V 200-kS/s rail-torail 8-bit successive approximation ADC[J].IEEE J.Solid-State Circuits,vol.42,no.10,pp.2161-2168,Jul.2007.
[8]R.R.Singh et al.Multi-step binary-weighted capacitive digital-toanalog converter architecture[J].in Proc.IEEE MWSCAS,Aug.2008,pp.470-473.
[9]R.J.Baker,CMOS Circuit Design,Layout,and Simulation,2nd ed[M].New York:Wiley,2004.
[10]E.Culurciello and A.G.Andreou.An 8-bit 800-uW 1.23-MS/s successive approximationADCin SOI[J].IEEE Trans.Circuits Syst.II,Exp.Briefs,vol.53,no.9,pp.858-861,Sep.2006.
[11]Y.Zhu et al.A 10-bit 100-MS/s reference-free SAR ADC in 90 nm CMOS[J].IEEE J.Solid-State Circuits,vol.45,no.6,pp.1111-1121,Jun.2010.
[12]Y.Zhu,U.Chio,H.Wei,S.Sin,S.U,and R.P.Martins,A powerefficient capacitor structure for high-speed charge recycling SAR ADCs[J].in Proc.IEEE ICECS.,Sep.2008,pp.642-645.

