基于信息熵权法和灰色关联度法的水资源综合效益评价

乌仁娜

(新疆博尔塔拉水文勘测局，新疆 博尔塔拉 834000)

水资源是一切生物赖以生存的必须物质，人类社会的工业、农业发展均离不开水资源的支撑[1]。然而人口的急剧增长、工农业发展速度过快，导致水资源缺乏及污染问题日益严重，严重影响了居民正常生活，制约了经济发展[2- 3]。针对现如今严峻的水资源形势，我国主要颁布了节水优先、治污为本、多渠道开源的措施[4- 5]，以最大限度解决水资源缺乏问题。水资源优化配置是解决目前水资源短缺问题最主要的措施之一，现如今遗传算法[6]、人工蚁群算法[7]已逐渐应用于水资源优化配置中，大大增加了水资源优化配置的准确性。对灌区水资源效益进行综合评价，可为水资源优化配置提供参考，使优化配置方案发挥最大效益，现实意义巨大，因此找出合适的方法评价水资源综合效益，已成为了国内水资源保护方面研究的重点。

目前针对水资源综合效益的评价方法，国内已有了部分研究。赵西宁等[8]在黄土高原评价了雨水资源化综合效益，以层次分析法为研究方法，建立了生态效益、经济效益和社会效益共32项指标的综合评价指标体系；赵洪杰和唐善德[9]、周维博和李佩成[10]分别在黑河中游灌区和干旱半干旱地区灌区，利用层次分析法，建立了水资源效益综合评价指标体系，并对灌区水资源综合效益进行了评价。现如今的水资源综合效益方法多采用层次分析法，该方法构建出的数学模型，将复杂的问题简单化，结果主观性太强，无法完全反映水资源效益的客观事实。

1 研究方法简介

1.1 信息熵权法

本文基于改进信息熵权法对灌区水资源综合效益进行评价，同时发出100份问卷调查，调查不同专家学者对各指标权重的评定，将信息熵权重(客观权重)与专家权重(主观权重)进行综合，得出综合权重，该权重既可以反映客观事实，也可反映主观专家意见，具有一定的代表性，客观权重与综合权重计算过程如下：

假设有m个对象，n个被评价指标，熵定义为：

(1)

(2)

式中，Hj—计算的信息熵；m—评价对象个数；n—待评价指标个数；bij—计算的相对隶属度；fij—相对隶属度所占比例。

对各项指标进行无量纲化处理，得出相对隶属度：

(3)

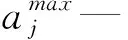
计算第j项指标的变异度：

Dj=1-Hj

(4)

式中，Dj—求的变异度；Hj—指标的信息熵。

计算该指标所对应的熵权重(客观权重)：

(5)

式中，ωbj—所求的客观权重；Dj—某项指标的变异度。

根据专家经验得出的主观权重与计算得出的客观权重，得出综合权重：

(6)

式中，ωj—所求的综合权重；ωaj—通过问卷调查所得的主观权重；ωbj—所求的客观权重。

1.2 灰色关联度分析法

灰色关联度分析法是近代新型综合评价方法。由于其对样本量的要求较低，计算简单，通俗易懂，结果可较强反映样本之间的客观关系等优点已逐渐被广泛应用。其具体步骤如下：

对于一个最优数列x0有若干个比较数列x1，x2，…，xn，关联系数ξ(xi)：

(7)

式中，ρ—分辨系数，一般在0～1之间，通常取0.5；Δmin—两级最小差；Δmax—两级最大差；Δoi(k) —各值与最优值之差。

由计算得到的ξ(xi)，计算关联度，并以关联度的大小排序。

1.3 评价指标体系构建

由于水资源的经济、社会和生态3个属性，因此水资源综合效益主要包括经济效益、社会效益和生态效益3个层面。本文基于信息熵权法和灰色关联度分析法，从经济效益、社会效益和生态效益3个方面，分别选取灌溉水利用系数C11、复种系数C12、综合灌溉定额C13、单位水粮食产量C14、人均GDP占有量C21、农民年收入C22、灌区年节水量C23、农民节水意识程度C24、森林覆盖率C31、污水处理率C32、垃圾无害化处理量C33、沙尘暴降低指数C34共12项指标，综合判定区域水资源综合效益。

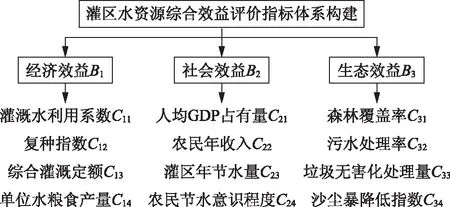
图1 水资源综合效益评价指标体系构建

2 工程实例分析

灌区位于新疆西北部博尔塔拉自治州，流域总面积12000km2，灌区面积超过160万亩，属于大(Ⅰ)型灌区，灌区所在区域年平均降水量215mm，年蒸发量1620mm，水资源总量达16亿m3，水资源总量分配不均、灌区设备老化、水资源管理制定不完善一直是制约灌区发展的主要因素，因此确定合适的水资源利用方法，对灌区水资源优化配置，提高水资源利用率意义重大。

分析2003、2008、2010、2015年四年的数据，根据公式(3)确定不同指标的相对隶属度矩阵，结果见表1。根据表1中的数据，可根据统计数据的客观性与1.1节中的公式计算各指标的客观权重，与专家调查的主观权重相比，信息熵权法计算结果基本与主观权重一致，由主观权重和客观权重，可综合得出第3层指标的初始综合权重，结果见表2。

根据表2中的数据，综合得出第2层指标的相对隶属度矩阵，从而计算出第2层指标的计算权重，其中经济效益指标的权重为0.53，生态效益指标的权重为0.25，社会效益的指标权重为0.22。根据第2层指标权重与第3层指标的初始综合权重，求得第3层指标的最终权重，结果见表3。

根据式(7)计算第3层指标的关联系数，结果见表4。根据表3种的最终综合权重，对表4中的数据进行综合加权，得出每一年不同指标的综合加权关联系数，结果见表5。

根据表5中的结果可知，将不同年份的水资源综合效益按最大到小排列依次为：2015年0.952、2010年0.583、2008年0.329、2003年0.202，表明灌区水资源效益情况呈逐年上升趋势，尤其是2010年之后，上升显著，符合水资源优化配置的要求，同时与灌区实际情况相符，因此计算过程正确，该方法具有一定的科学性。

表1 第三层指标相对隶属度矩阵

表2 第三层指标初始综合权重

表3 第三层指标最终综合权重

表4 第三层指标灰色关联系数

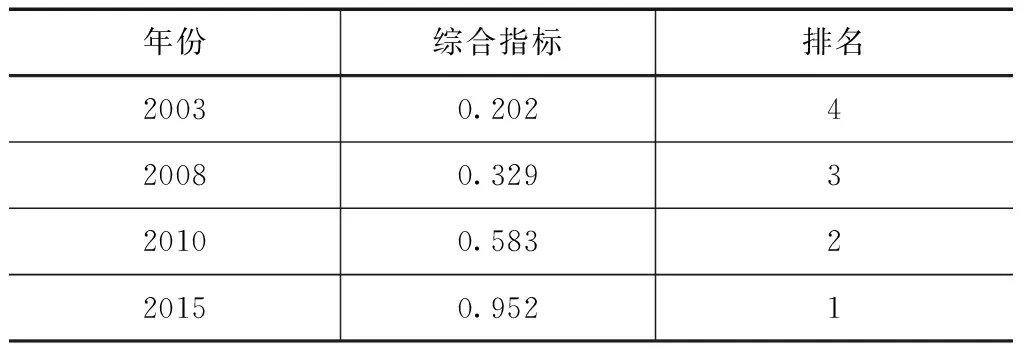
表5 不同年份水资源综合效益排名

3 结语

本文基于信息熵权法与灰色关联度法的综合分析方法，对灌区水资源综合效益进行了评价，建立了经济效益、社会效益和生态效益共12项指标的评价指标体系。通过计算不同指标的综合权重和灰色关联系数，得出综合关联系数，该方法最大程度上消除了评价方法的主观性，同时对2003、2008、2010、2015年的水资源综合效益进行了评价，指出2015年的灌区水资源综合效益最高，符合实际要求，证明了该方法的准确性。

[1] 吕素冰, 许士国, 陈守煜. 水资源效益综合评价的可变模糊决策理论及应用[J]. 大连理工大学学报, 2011, 51(02): 269- 273.

[2] 田浪, 刘永强, 王珍, 等. 基于物元可拓模型的灌区水资源综合效益评价[J]. 排管机械工程学报, 2016, 34(04): 351- 356.

[3] 陆宝龙, 陈发斌. 兰州市水资源利用分析与优化配置方案研究[J]. 水利规划与设计, 2017(10): 67- 72.

[4] 左其亭, 陈嚷. 面向可持续发展的水资源规划与管理[M]. 北京: 中国水利水电出版社, 2003.

[5] 钱易. 水资源管理需要新思路新策略[J]. 中国水利, 2002(10): 17- 20.

[6] 潘俊, 王灏瀚. 基于遗传算法的多目标水资源优化配置——以沈阳地区为例[J]. 沈阳建筑大学学报(自然科学版), 2016, 32(05): 945- 952.

[7] 李苏, 刘彬. 改进的人工鱼群算法在邯郸市水资源优化配置中的应用[J]. 水电能源科学, 2016, 34(12): 10- 14.

[8] 赵西宁, 冯浩, 吴普特, 等. 黄土高原小流域雨水资源化综合效益评价指标体系研究[J]. 2005, 20(03): 354- 360.

[9] 赵洪杰, 唐善德. 黑河中游灌区水资源综合效益评价体系研究[J]. 节水灌溉, 2006(06): 58- 62.

[10] 周维博, 李佩成. 干旱半干旱地域灌区水资源综合效益评价体系[J]. 自然资源学报, 2003, 18(30): 288- 293.