弯道水流调整池结构参数对流态改善能力的影响

赵 丹

(抚顺县水利水电工程移民局，辽宁 抚顺 113118)

由于弯道水流存在波浪、螺旋翻滚和水面横向坡等特殊特征逐步变成研究水建筑物合理布置、防淤治沙和河床演变等目标的重要先决条件[2]。寻得一种结构简单、造价低廉和施工快捷的工程措施显得十分重要[2]。王艳梅[3]发现了一种设计简单、施工方便的“弯道水流调整池”，能够有效地改善弯道水流流态；赵德亮[4]运用三维流场数值模拟模拟了拦河闸引水口弯道湍流分离流动，证明该模型能够良好的模拟强曲率下湍流的分离现象；张应亮[5]等通过分析分流墩与消力池联合应用消能效果，模拟了弯道流速的分布及液面形态的变化。本文通过对弯角弯道90°不同纵坡角下水流流态改善能力随着深度、长度变化情况进行了研究，为工程实际应用提供了设计依据。

1 弯道调整池流态模拟

1.1 离散方程求解算法

控制方程离散后需要根据特定的方法对其进行计算，常用的求解方法包括PISO算法、SIMPLEC算法和SIMPLE算法[6- 7]。PISO算法基于压力速度校正的近似关系，执行偏斜校正、相邻校正与临近校正计算，经过若干循环，得到满足动量方程和质量守恒的校正速度。SIMPLE算法以交错网格技术为基础，以“预测—修正”为核心思想，经过持续的修正、迭代，得到速度和压强的初解，再通过修正目标得到满足质量守恒方程的精确解。本文采用SIMPLE算法进行求解。

1.2 自由液面评价高度

根据水面波动设计一个定量分析值称作自由液面评价高度，采用增加缩放系数来控制水面评价高度[8- 9]。表达公式如下：

(1)

式中，Xi—监测面水面线的最高与最低位置的差值；i—断面；m—弯道部分断面数；n-m—直道部分断面数。

2 弯道水流调整池参数变动对流态的影响及分析

本文研究了弯角弯道90°水流调整池流态改善能力随着深度、参数变化情况，如图1所示。流态改善能力选择自由液面评价高度L与其波动情况作为评价标尺，观察不同参数下调整池后弯道左右边界与中央水面线情况[10]。弯道调整池的消能能力根据弯道出口断面7、进池平面断面1与出池平面断面2的平均水头进行判断，根据该模型调整池的相关数据分析弯道水流调整池流态改善的规律性。

2.1 纵坡角为1°情况下参数变动结果

2.1.1 深度参数变动结果

图2给出了当纵坡角为1°时，深度参数变动调整池后中央及左右岸边水面线情况。

图1 弯道模型示意图

对比图2(a)～(d)中可以看出，纵坡脚较小的弯道，设置有调整池的直道水流相比未设置调整池的直道水流波动更加平稳，并且随着调整池深度的增加，直道水流的波动变化更加稳定；设置有调整池的弯道最高水深相比未设置调整池的弯道最高水深更高，高深度调整池的最大弯道高度也高于低深度的弯道最大调整池，具有较好的工程实用性。

表1为纵坡角1°、弯道弯角90°下弯道调整池深度参数变化相关数据。

由表1可以看出，自由液面评价高度只有调整池深度为5cm时相对较大，而随着调整池深度的增加没有良好改善，同时调整池深度较深的情况下出现了自由液面评价高度升高的情况。断面7切向流速随着调整池深度的增大急速增大，并且远大于未设置调整池的切向速度，调整池的消能能力随着深度的改变没有得到改善。因此，本文认为纵坡角为1°弯道调整池深度不宜过高，设置5cm左右能够良好改善水面坡降。

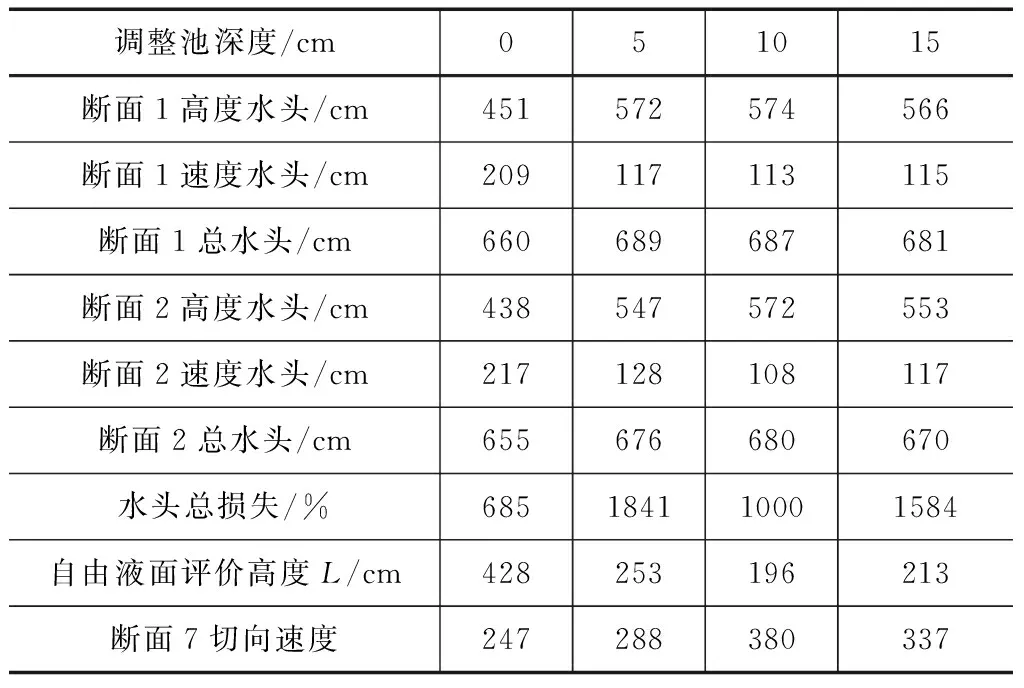
表1 纵坡角1°、弯道弯角90°下弯道调整池深度参数变化相关数据

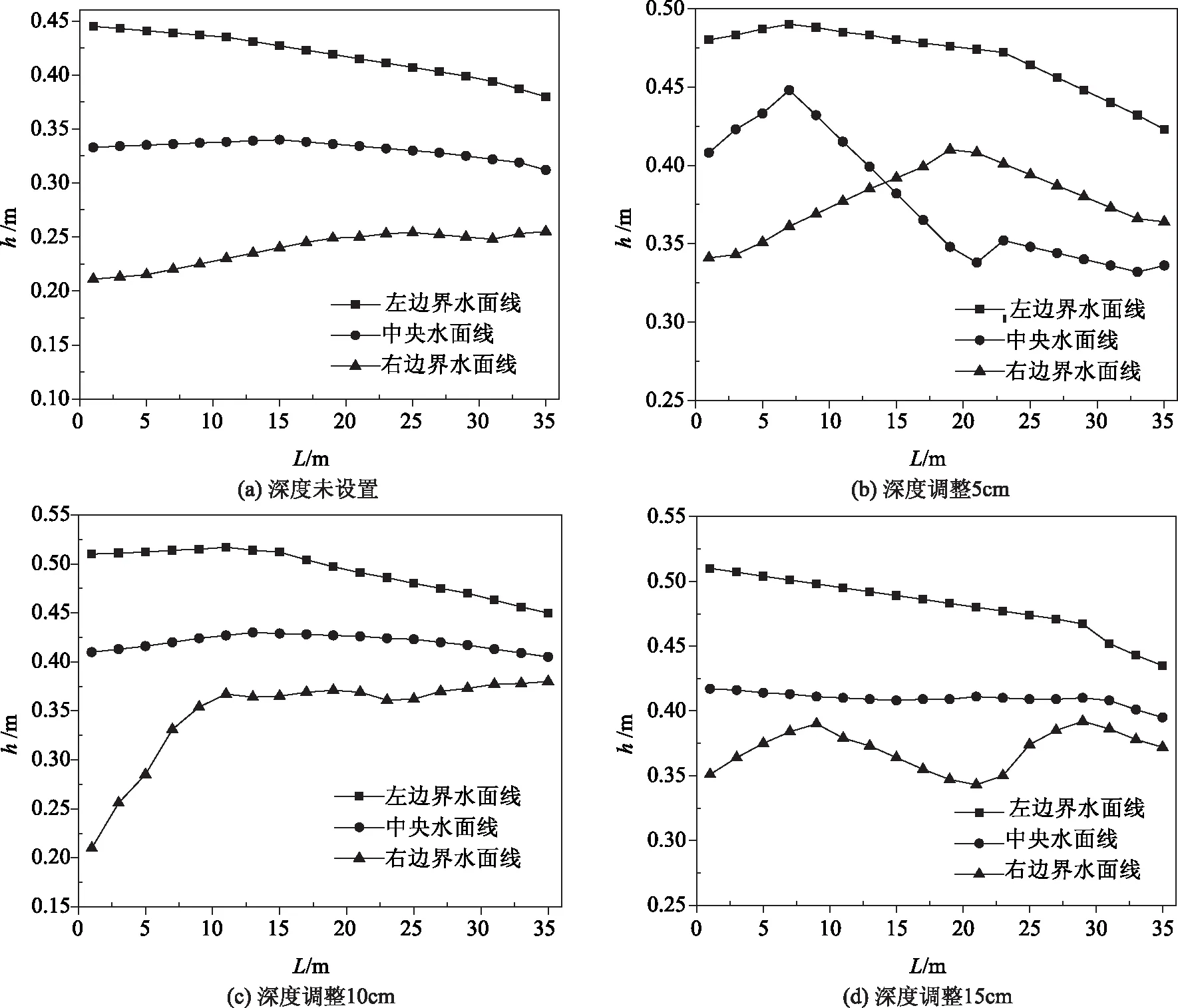
图2 纵坡角1°深度参数变动调整池后中央及左右岸边水面线情况

2.1.2 长度参数变动结果

图3给出了当纵坡角为1°时，长度参数变动调整池后中央及左右岸边水面线情况。

对比图3(a)～(d)中可以看出，纵坡角为1°弯道弯角为90°调整池长度为20cm时，其弯道水面线改善情况并不明显，接近于未设置调整池时的情况，而其弯道波动随着调整池长度的增加显著增强。通过对比中央水平面有无调整池的情况发现，其波动随着调整池长度的增加变得越来越明显。

表2为纵坡角1°、弯道弯角90°下弯道调整池长度变化相关数据。

由表2可以看出，与相比未设置调整池的情况相比设置不同长度的弯道调整池都存在较大的改善，其中断面1高度水头、断面2高度水头和自由液面评价高度大幅度降低，断面1速度水头和断面2速度水头小幅度的增加，断面1总水头和断面2总水头无明显增加。水头损失情况并无明显规律，而整体趋势随着长度增加而增大，随着深度的改变调整池的消能情况没有得到改善，结合实际工程施工的需要，本文认为该弯道调整池长度选择20cm最佳。

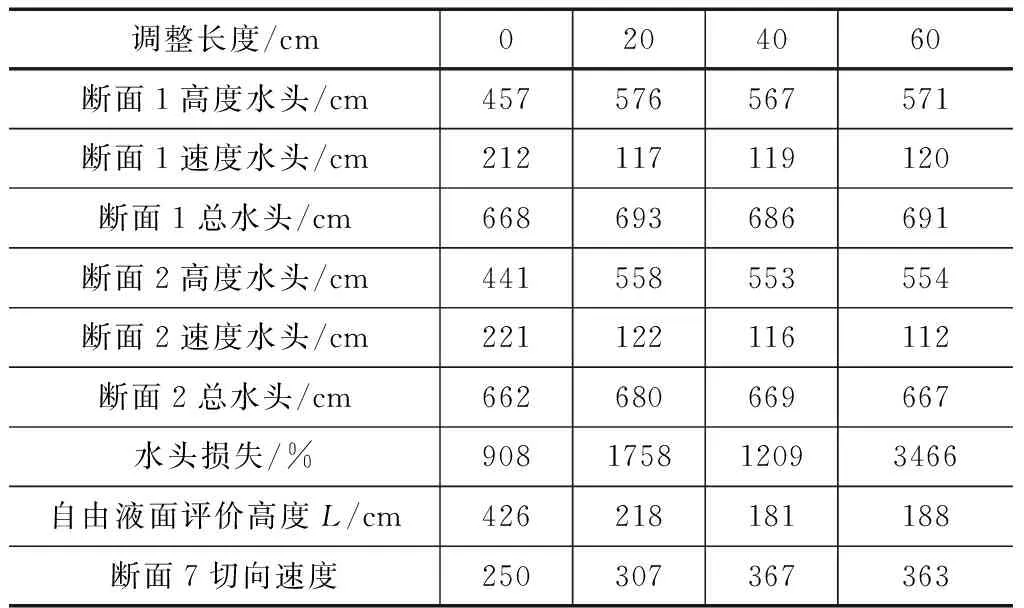
表2 纵坡角1°、弯道弯角90°下弯道调整池长度变化相关数据

2.2 纵坡角为3°情况下参数变动结果

2.2.1 深度参数变动结果

图4给出了当纵坡角为3°时，深度参数变动调整池后中央及左右岸边水面线情况。

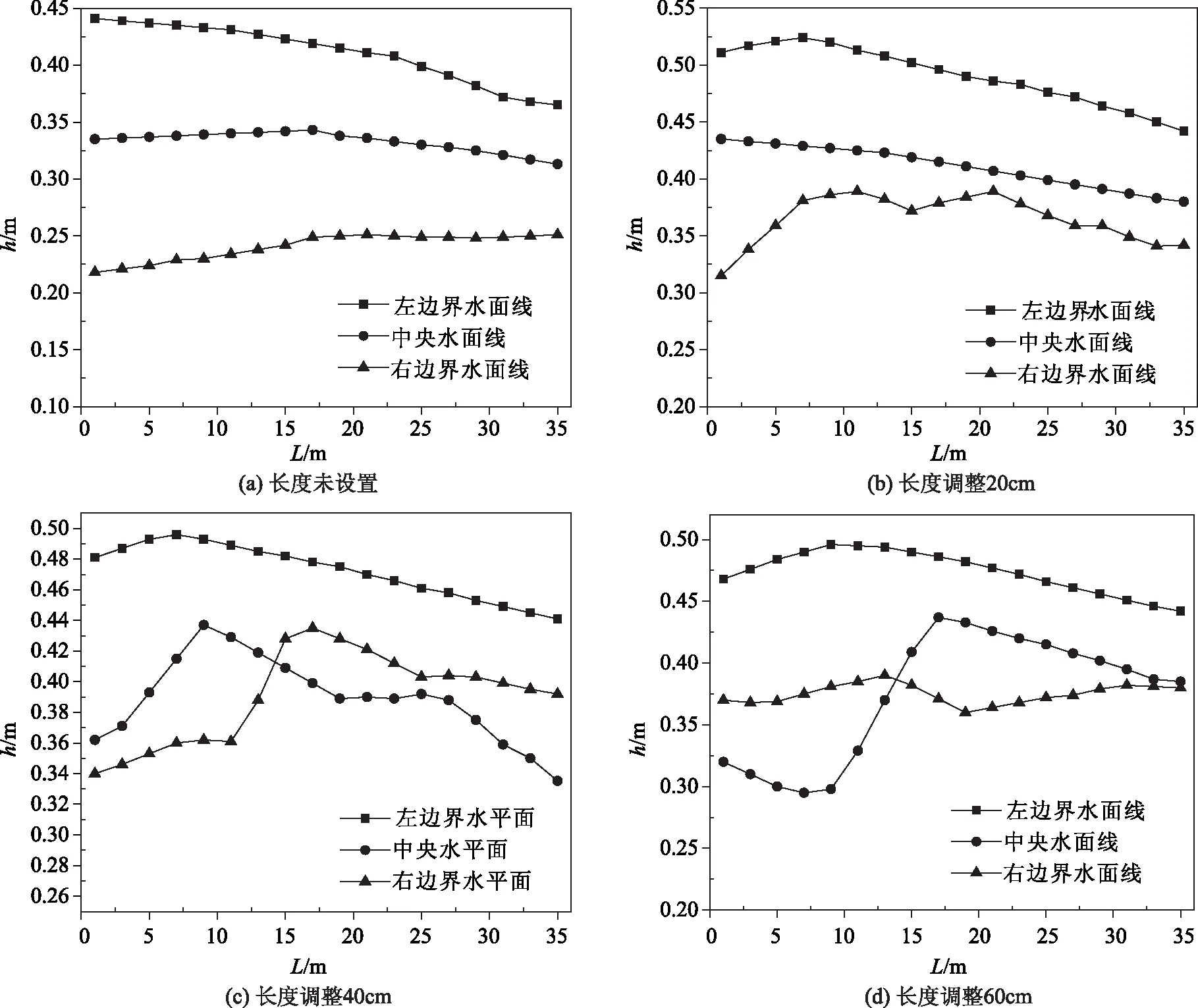
图3 纵坡角1°长度参数变动调整池后中央及左右岸边水面线情况

对比图4(a)～(d)中可以看出，设置有调整池的直道水流相比未设置调整池的直道水流波动更加平稳，调整池深度调整5cm时直道部分的水面波动具有明显改善，但是这种改善随着深度的增加并不持续变大，这一点与纵坡角1°、弯道弯角90°的情况相同，而与纵坡角1°的情况相比，调整池的深度设置较小也能够使弯道水面线产生明显的水面线波动。

表3为纵坡角3°、弯道弯角90°下弯道调整池深度参数变化相关数据。

由表3可以看出，相比于未设置调整池的自由液面评价高度，调整池深度为5cm和10cm时情况改善显著，调整池深度为15cm时无较大的改观，断面1高度水头和断面2高度水头随着调整池深度的增加而增长，断面1速度水头与断面2速度水头随着调整池深度的增加而整体降低，断面1总水头和断面2总水头略微减小。结合水面线情况，本文认为纵坡角3°弯道弯角90°情况下，应当选择调整池深度为10cm。

表3 纵坡角3°、弯道弯角90°下弯道调整池深度参数变化相关数据

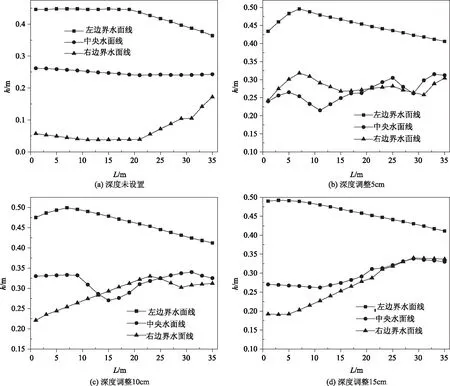
图4 纵坡角3°深度参数变动调整池后中央及左右岸边水面线情况

2.2.2 长度参数变动结果

图5给出了当纵坡角为3°时，长度参数变动调整池后中央及左右岸边水面线情况。

对比图5(a)～(d)中可以看出，直道中的改善情况在调整池池深设置40～60cm明显优于调整池池深设置20cm。

表4为纵坡角3°、弯道弯角90°下弯道调整池长度变化相关数据。

由表4可以看出，自由液面评价高度随着调整长度的增加而显著下降，并且当调整长度达到60cm时，断面7的切向速度存在相当水平的降低，结合观察到的水面线情况，综合认为纵坡角3°、弯道弯角90°的较佳长度为60cm。但是相比于未设置调整池的情况而言，调整池的消能表现并不理想。

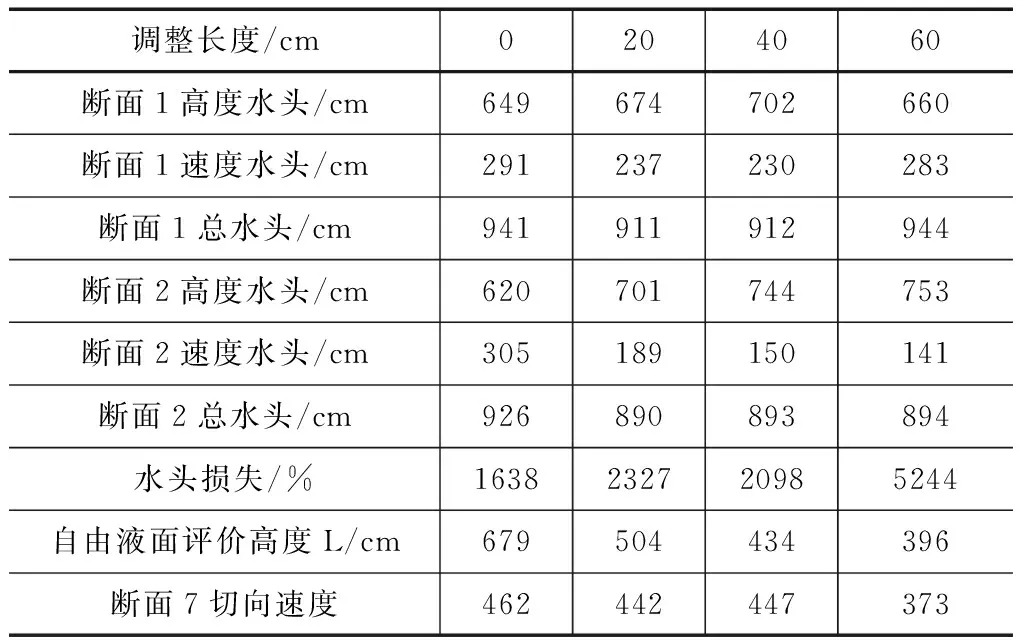
表4 纵坡角3°、弯道弯角90°下弯道调整池长度变化相关数据

3 结语

按照相关弯道调整池流态模拟方法，选择自由液面评价高度L与其波动情况作为评价标尺，研究弯角弯道90°不同纵坡角下水流调整池流态改善能力随着深度、参数变化情况。

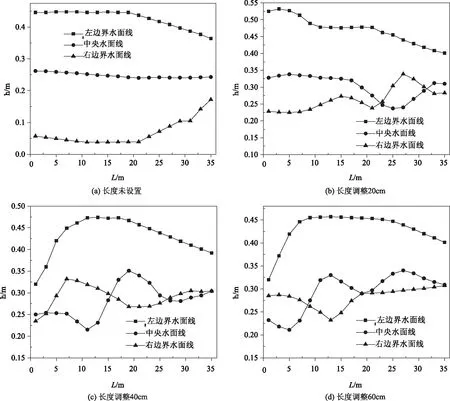
图5 纵坡角3°长度参数变动调整池后中央及左右岸边水面线情况

(1)设置有调整池的直道水流相比未设置调整池的直道水流波动更加平稳，设置有调整池的弯道最高水深相比未设置调整池的弯道最高水深更高。

(2)弯道波动随着调整池长度的增加显著增强，该弯道调整池长度选择20cm最佳。

(3)调整池的深度设置较小也能够使弯道水面线产生明显的水面线波动，并且认为纵坡角3°弯道弯角90°情况下，应当选择调整池深度为10cm。

(4)调整长度为60cm时，断面7的切向速度存在相当水平的降低，因此认为纵坡角3°、弯道弯角90°的最佳长度为60cm。

[1] 逄焕春. 新疆玛纳斯河弯道式引水渠首引水防沙技术研究[J].

水利规划与设计, 2013(08): 51- 52.

[2] 逄焕春. 新疆玛纳斯河弯道式引水渠首运行经验[J]. 水利技术监督, 2012, 20(04): 39- 41.

[3] 王艳梅, 杨玲霞, 周明, 等. 拟U型弯道急流流态的调控措施研究[J]. 水电能源科学, 2015(07): 94- 96.

[4] 赵德亮, 朱萍. 宽尾墩对跌坎底流消力池影响的试验研究[J]. 水利建设与管理, 2015, 35(02): 31- 34.

[5] 张应亮. 桂花水电站掺气分流墩与消力池联合应用消能效果的研究[J]. 中国水能及电气化, 2011(08): 39- 44.

[6] 张桂花, 张一冰, 高继东, 等. 溢洪道弯道水流流态与消力池尾水坎型式[J]. 南水北调与水利科技, 2015(02): 40- 42.

[7] 李润清. 关于强弯河道水流结构及离散特性分析[J]. 水利规划与设计, 2017(06): 93- 95.

[8] 邓春艳, 夏军强, 宗全利, 等. 二次流对微弯河段水沙输移影响的数值模拟研究[J]. 泥沙研究, 2013(05): 27- 34.

[9] 刘佳星. 动床弯道水流结构调整的实验研究[D]. 华北水利水电大学, 2015.

[10] 高传昌, 解克宇, 黄丹, 等. 不同水位对泵站进水池流态影响的数值模拟[J]. 华北水利水电大学学报(自然科学版), 2015, 36(06):10- 14.