变糙率二维水流泥沙数学模型在河道行洪能力分析中的应用

辛 波

(辽宁省丹东水文局，辽宁 丹东 118000)

当前，河道整治后需要对河道的行洪能力进行评估，需要对河道整治前后的流态、水位以及冲淤变化进行分析，近些年来，国内许多学者结合一维、二维水力学数学模型对河道整治工程前后河道行洪能力进行过相关研究[1- 7]，在一维和二维水力学数学模型中大都需要对河道糙率进行合理选取，而不同流量、水位下河道糙率有所不同，传统方法大多设置固定糙率对河道整治工程后的行洪能力进行分析，而这种方式往往使得河道行洪能力计算有所偏差。近期有学者研究了不同流量下变动糙率计算方法，并结合变糙率方法对长江的河道洪水进行预测分析[8]，分析结果表明相比于传统糙率方法，变糙率方法在糙率的选取更为合理，且对河道洪水预测精度有明显提高。为此本文引入变糙率方法并结合二维水流泥沙数学模型对河道整治工程后的行洪能力进行分析，分析方法将为河道整治工程行洪能力分析提高方法参考。

1 变糙率二维水流泥沙数学模型原理

二维水流泥沙数学模型采用以下质量连续方程对水量和泥沙进行二维演进计算，计算方程为：

(1)

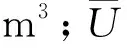
二维水流泥沙数学模型采用以下方程进行动能计算，计算方程为：

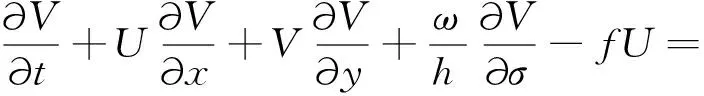
(2)

式中，Px、Py—垂向和水平方向的压力，kN；ρ0—水的密度常数，1.0×103kg/m3；FX、FY—计算雷诺数；u、v—不同方向上的计算流速，m3/s；Mx、MY—河道水流外部动量，kg·m/s；f—科氏影响系数；g—重力学加速度，m/s2；ω—纵向方向的计算流速，m3/s。

模型采用以下方程计算垂向和水平方向的压力Px和Py，计算方程为：

(3)

相比于大尺度二维水流泥沙数学模型，雷诺数计算的公式可以简化为下面两个方程：

(4)

(5)

式中，vH—计算单元内水平方向上黏滞系数；其他变量同式(2)和(3)中变量含义。

变糙率方程引入函数方程对糙率进行优化取值，对不同流量、水位下的糙率进行优选，计算方程为：

(6)

式中，nr—糙率初始参照值；ai、bi—计算常数，不同流量下ai和bi的取值不同；q—流量；Q1、Q2—流量上、下限。

2 模型应用

2.1 河道整治概况

研究河流干流长3.0km。河底高程2.0～4.8m，河底宽10～20m，河面宽100～120m，堤线长3.0km。现状堤顶高程11.4～12.8m，堤顶宽5.5～12.5m，有宽3m左右泥结碎石路面；迎水坡比大部分地段约1∶3，局部较陡处约1∶2.5，基本无护砌，杂草丛生，背水坡坡比1∶2.5～1∶3.5；入江口段200m及距入江口1.47km至1.65km段有挡浪墙，左岸墙顶高程12.0～12.7m，右岸13.0m。距河口2km建有橡胶坝，坝顶高程8.3m。

通过二维水流泥沙输运数学模型对工程进行了2个工程方案研究。方案1：在天然情况下，研究区域的水位、水流流态特征、冲淤情况。方案2：在工程完成后的水位、水流流态特征、冲淤情况。对比在工程前后的水位、水流流态特征、冲淤情况。在数学模型中，将研究区域划分为纵向329个，横向48个计算网格，网格的纵向尺寸为1～5m，横向尺寸为0.7～1.2m，计算网格以及地形能较好的反映研究区域工程前后的地形变化。研究河道计算网格如图1所示。

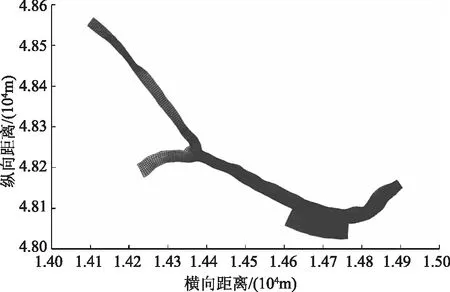
图1 研究河道网格剖分图

2.2 不同糙率方法的二维水流泥沙数学模型的流态精度对比分析

为对比分析变糙率和传统糙率方法二维水流泥沙数学模型的水力学精度，选取5个典型断面，对各典型断面进行了流速和水位的试验测定，结合试验测定的数据对比分析不同糙率方法下二维水流泥沙数学模型的流态模拟精度。对比结果见表1、2。

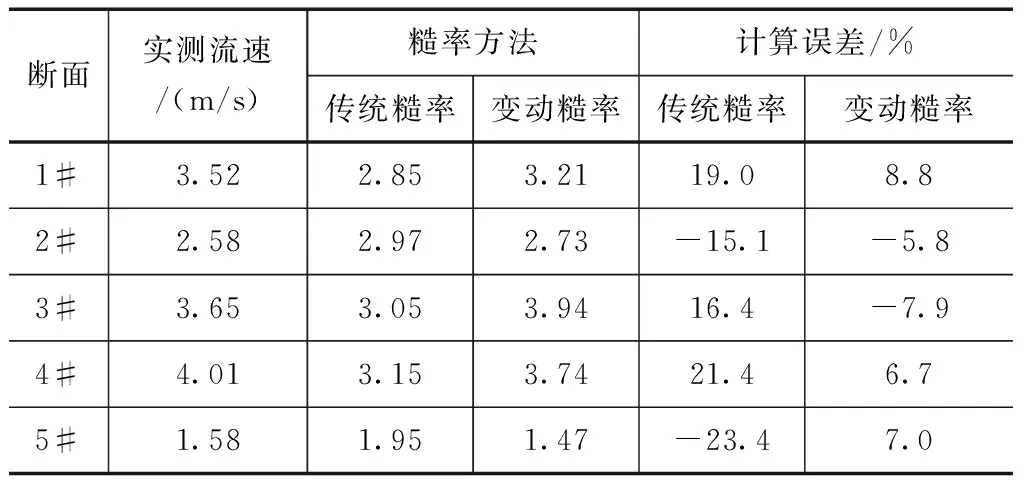
表1 不同糙率方法下二维水流泥沙流速模拟精度对比结果

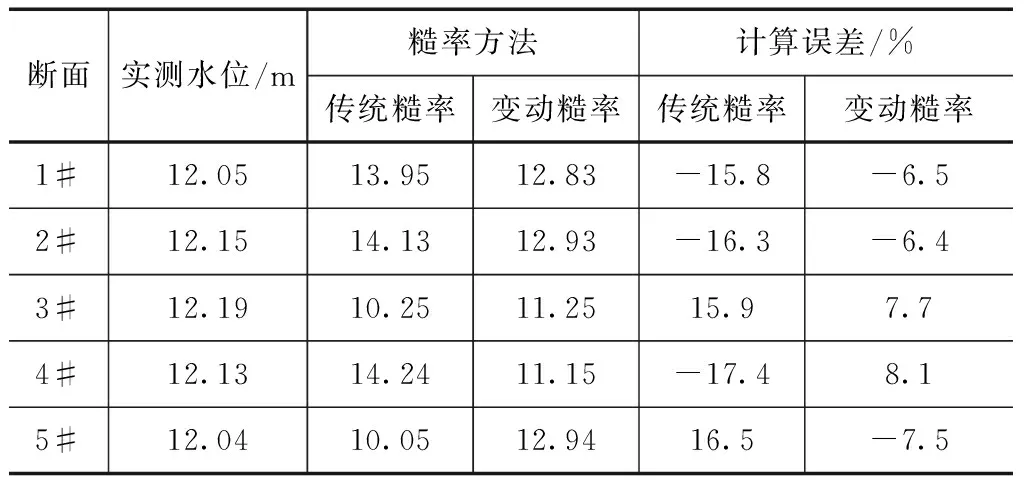
表2 不同糙率方法下二维水流泥沙水位模拟精度对比结果

从表1中可以看出，变糙率方法下的流速计算误差较传统固定方法计算误差有明显改善，变糙率方法下二维水流泥沙数学模型在各计算断面下的流速计算误差均小于10%，而传统固定糙率方法下二维水流泥沙数学模型下计算流速误差在15%以上，计算误差在-15.1%～-23.4%之间，相比于传统固定糙率方法，变糙率方法在流速计算误差上均值减少11.8%。这主要是因为变糙率方法可对不同流量下的糙率进行优化选值，计算结果好于传统固定糙率的方法。表2为不同糙率方法下各断面水位计算精度对比，从表2中也可明显看出，变糙率方法下水位计算误差也明显低于传统固定糙率的方法，相比而言，变糙率方法下的水位计算误差均值减少9.1%。

2.3 河道整治前后河道洪水水面线及洪水位模拟分析

考虑在最不安全的情况下，即在流量为以流域20年一遇降雨遭遇20一遇洪水情况下来分析。工程前后河道的水面线分布情况如图2所示。

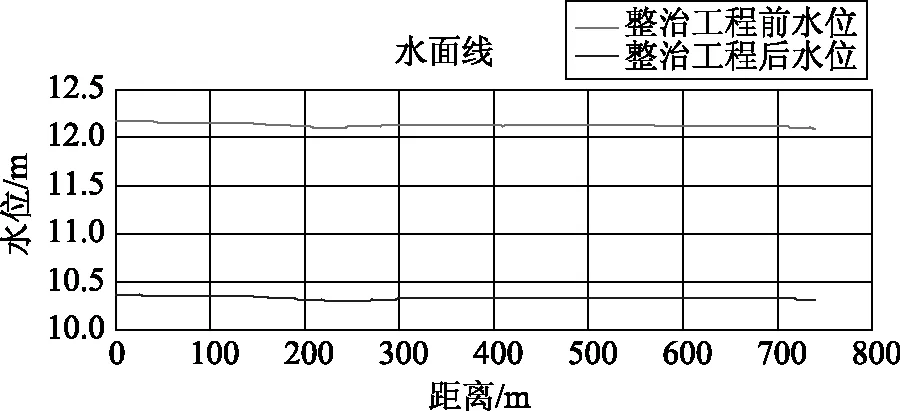
图2 河道改造前后洪水水位模拟结果

河道改造工程完成后，一方面河道的清淤，河床挖深近2m，增加了在同一水位下的过水面积，另一方面河道较改造工程前更为顺直，河道改变了原来的杂草丛生的状态，河道的糙率减小。河道改造工程增加了河道的过水能力，有利于河道防洪。河道改造工程完成后，河道的行洪能力增加。从图2中可以看出改造工程前河道的水位在12.10～12.20m之间，改造工程完成后，河道的水位在10.31～10.36m之间。计算的结果来也验证了河道改造工程增加了河道的行洪能力，在同一流量下，河道的水面线较河道改造工程前有所下降，总体上下降1.8m左右。

2.4 河道整治前后流速及流态模拟分析

为分析河道整治前后流速和流态的变化，结合变糙率下的二维水流泥沙数学模型对河道整治前后的流态进行动态模拟分析，河道整治前后的流速和流态动态分布结果如图3、4所示。

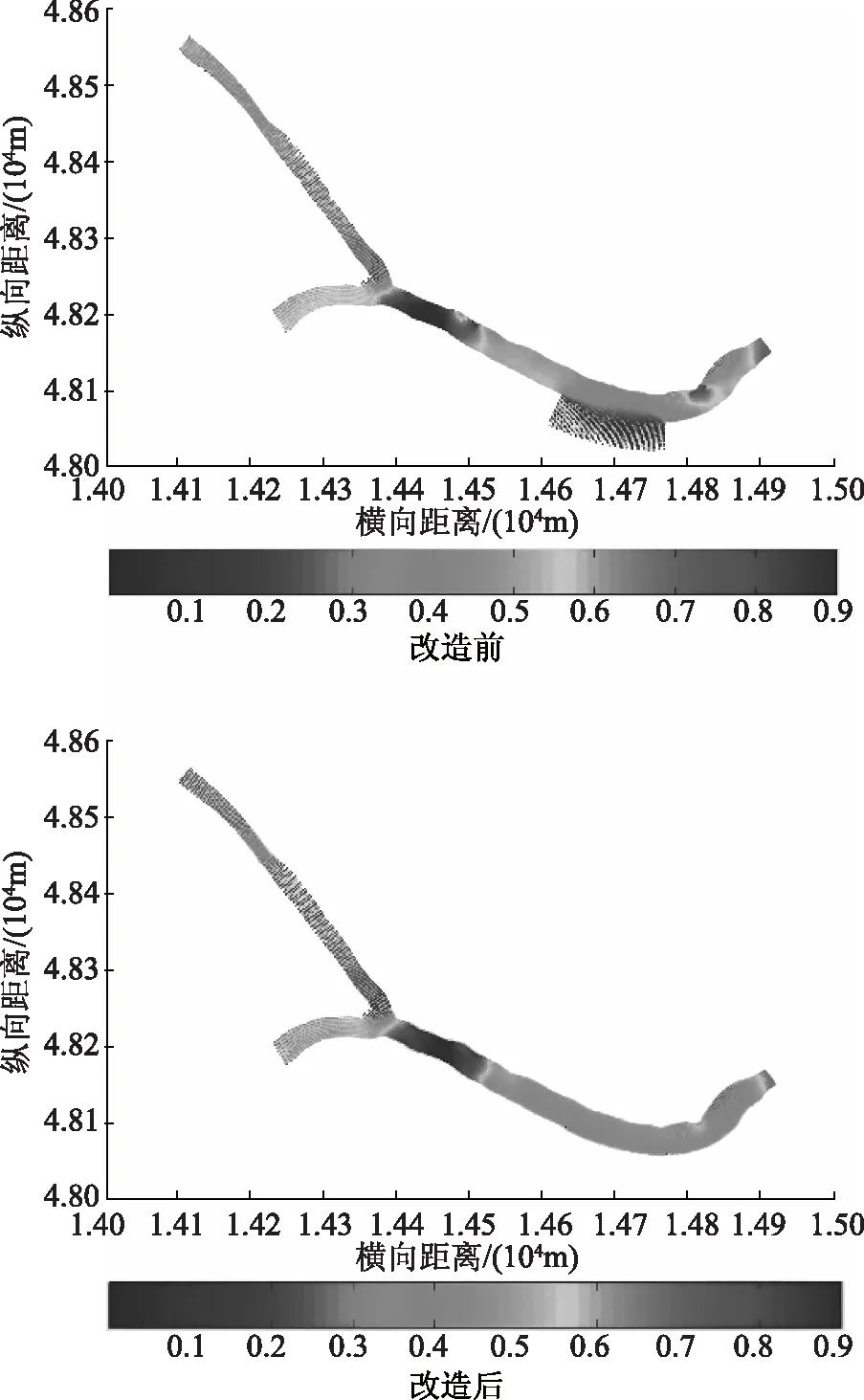
图3 河道改造前后流流态分布图

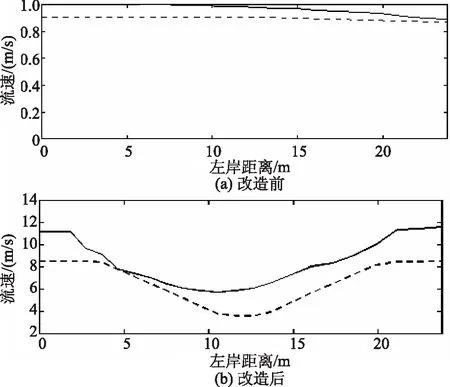
图4 河道改造前后典型断面流速分布图(实线：工程前，虚线：工程后)

从图3、4中可以看出工程完成前后，河道的流态如图4所示。在同一流量下，河道流速有所减小。各断面的流速对比如图所示。在工程中游区域，尽管断面的过水面积有所减小较大，但实际过流面积变化不大，流速虽有所增大，但增大的幅度较小。改造工程前后，在工程上游断面附近流速较大，注意防洪安全。各断面的流速分布对比如图所示，其中流速改变较大的区域，研究区域里有两座桥梁，两桥上游和到较窄，河道流速较大。相比较而言，两座桥对河道行洪的影响较河道狭窄的影响小。

2.5 河道整治前后冲刷淤积分析

考虑到河道改造工程完成后，采用浆砌片石进行河底护岸，在工程完成后的计算中，将此部分设置为不可冲刷。冲淤的计算结果如图5所示。

图5 河道改造前后河道冲淤变化分析

从图5中可以看出发生冲刷得主要部位在工程上游区域，侧冲刷明显。在工程完成后，由于采用浆砌片石进行河底护岸，其河道部分区域冲刷明显，主要位于河底护岸与清淤后的河底交接部位。因最大冲刷将近1m，对河底与护岸将产生影响。工程下游，因河道放宽，将产生一定淤积，工程完成后，淤积将有所减缓。因改造工程完成后，河道河底将普遍降低约2m，由此，一方面，将对工程区域上游河道产生溯源冲刷，另一方面，在工程区域内，也会有一逐渐自上游往下游的淤积过程。

2.6 行洪能力影响分析

本次工程对河道进行了清淤。河道清淤后，除局部河段由于拆迁困难等原因无法扩大河道断面外，大部分河道行洪断面比现状增加25%以上，较大地提高了河道的行洪能力。工程前后断面面积变化分析结果见表3。

3 结语

本文采用变糙率下的二维水流泥沙数学模型对河道整治后的行洪能力进行了数值模拟分析，分析取得以下结论：

(1)变糙率方法结合不同流量对糙率进行优选，提高了二维水流泥沙数学模型流态模拟精度，相比于传统固定糙率的方法，其流速和水位计算误差均值减少11.8%和9.1%。

(2)河道整治后，断面面积增大，行洪能力增加的同时，同一流量下的流速增幅变化较小。

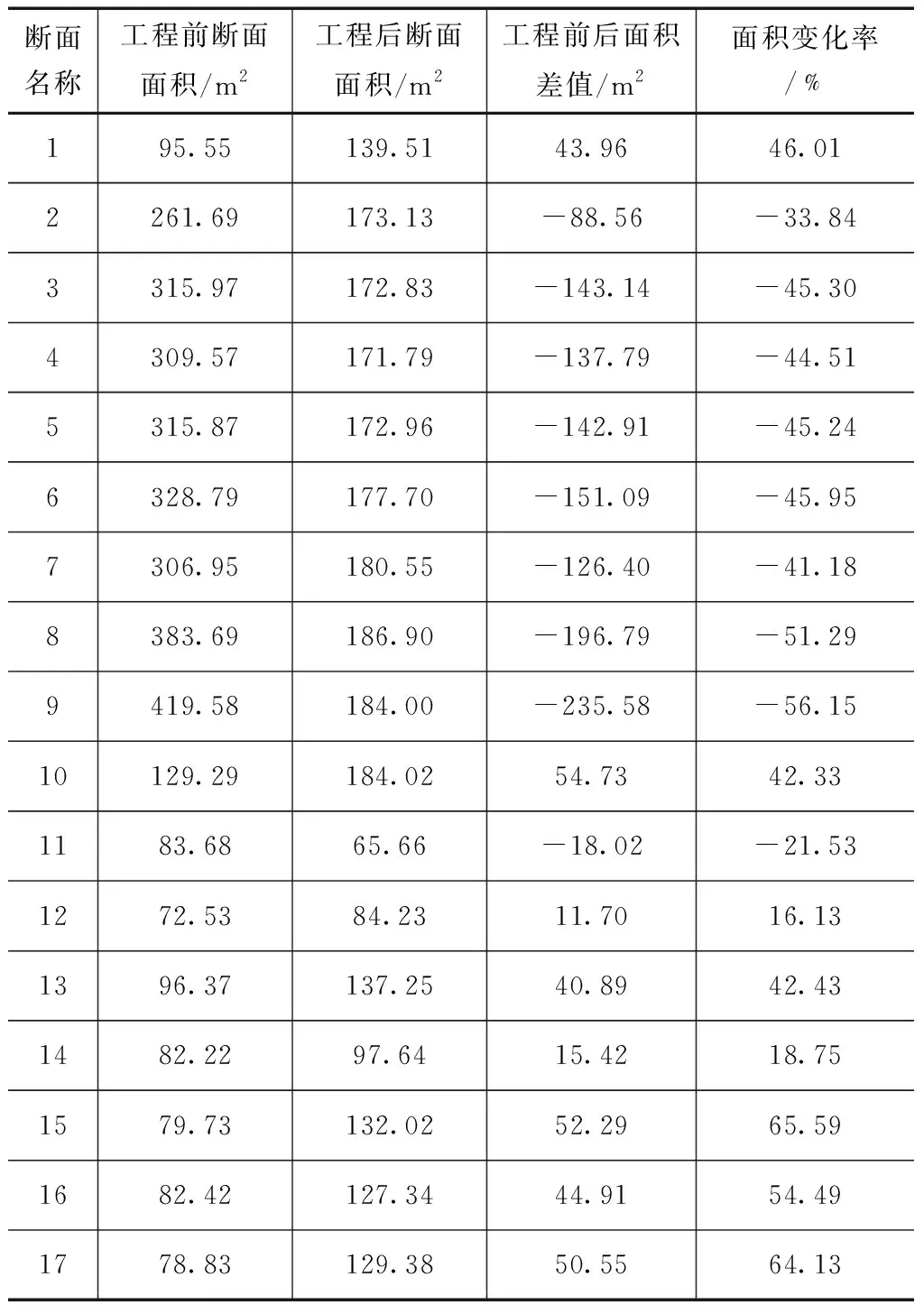
表3 设计水位工况下工程前后断面面积变化

(3)河道整治工程应注意上游河道产生的溯源冲刷，加大溯源冲刷的工程措施。

[1] 张旭. 有限元软件在河道整治工程中的应用[J]. 东北水利水电, 2015(11): 63- 65.

[2] 王蕊. 二维河道冲刷数学模型在河道冲刷物理模型试验中的应用研究[J]. 水利技术监督, 2017(03): 86- 88+153.

[3] 鲁俊蓉. 河道整治工程数值模拟分析[J]. 山西水利科技, 2013(04): 71- 73.

[4] 吕敏. 洪泛区河道行洪能力数值模拟研究[J]. 水利规划与设计, 2016(01): 33- 34+75.

[5] 刘强, 吴国芳. 基于MIKE 11 HD水动力模型的复杂河道水利计算[J]. 水利规划与设计, 201(07): 68- 70.

[6] 魏晓. 长江口北支地貌演化与河道整治的数值模拟[D]. 南京大学, 2012.

[7] 李天翔, 廖华胜, 刘期勇. 整治河道段流场计算中边界条件的影响[C]. 国际水利工程与研究协会中国分会、 中国水利学会水力学专业委员会、 中国水力发电工程学会水工水力学专业委员会. 第三届全国水力学与水利信息学大会论文集, 2007(08).

[8] 姜利玲, 汤成友, 曾适. 变糙率水力学模型在长江上游洪水预报中的应用初探[J]. 水利水电快报, 2017(04): 13- 16.