简析垂直简谐运动的合成

湖南省郴州市宜章县第四中学 李恪武

1.一个学生设计的运动模型

在讲简谐运动这一章里一个学生拿着一个自己设计的模型如图（1），让我给它解释小球的运动。图形如下：一个箱子里装着一个小弹簧振子，放在光滑水平面上，左右两边再连接弹簧构成一个大的弹簧振子。在大弹簧振子振动的同时，使小弹簧振子也开始振动。最终弹簧振子将做什么运动呢？学生自己想象的运动是圆周运动。

2.用运动合成的思想解决问题

无疑小球的运动是一个非常复杂的运动。但是从运动的合成角度来看小球参与了两个运动：水平方向：随箱子的左右振动，竖直方向：自身的上下振动。小球的最终运动是这两个振动的合运动。

3.两振子周期（也就是角速度）相同的几种特殊情况

为了具体,设大弹簧振子的振幅为A1，角速度为初相位为小弹簧振子的振幅为A2，角速度为初相位为先看一些特殊情况：

3.1.若则：

小球竖直方向的位移：

两式左右相比得到：①，两个简谐运动的合成竟然是一条直线！直线的斜率为正，斜率大小由两个振动的振幅比值决定。图形如图（2）：

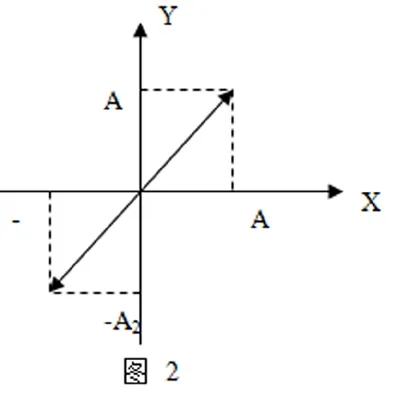
3.2.若则：

小球水平方向的位移：

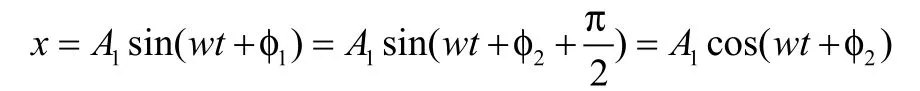
小球竖直方向的位移：

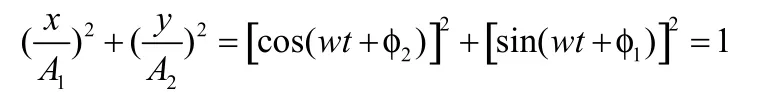
整理得

②,这是一个标准的椭圆方程。小球的运动轨迹是一个逆时针的椭圆，设A1＞ A2图形如图（3）：

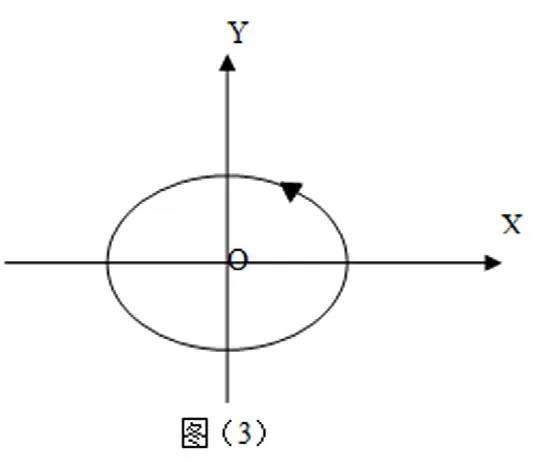
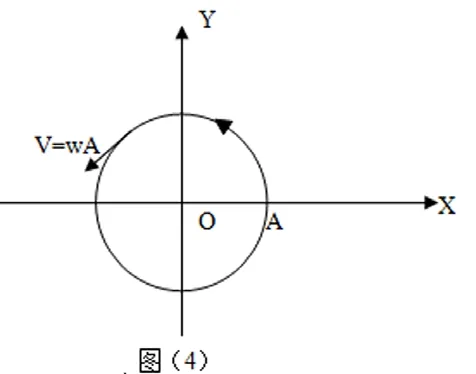
若A1=A2=A，②式变为小球将做一个逆时针的匀速圆周运动。半径为A，线速度轨迹图形如图（4）：

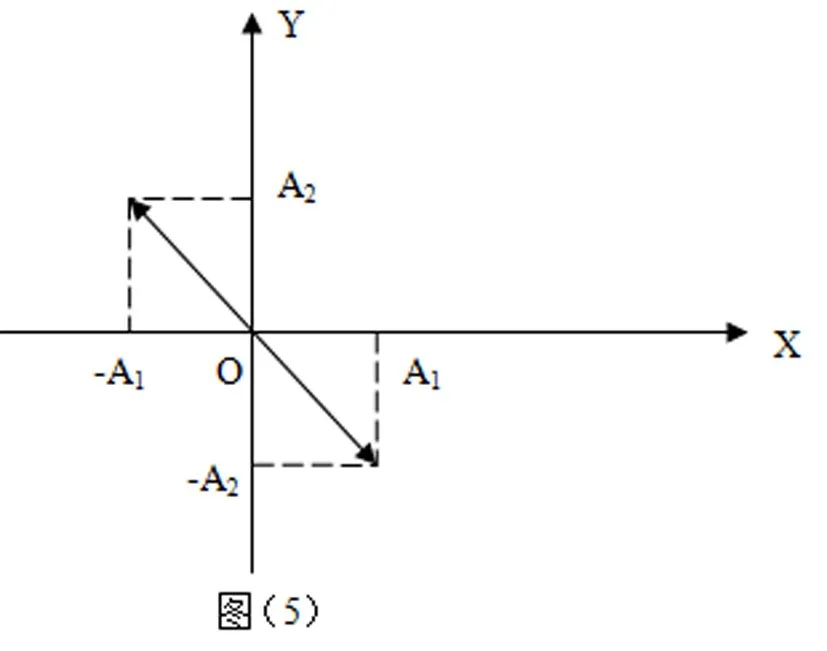
3.3.若则：

小球水平方向的位移：

小球竖直方向的位移：

3.4.若则：

小球水平方向的位移：

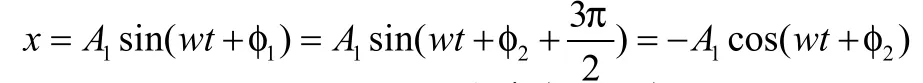
小球竖直方向的位移：

通过上面特殊情况的分析知道当角速度相同的时候，小球的运动主要是三种：直线运动，圆周运动，椭圆运动。对一般相位差分析发现除了这几种特殊情况以外，小球的一般运动为椭圆。

4.一般情况分析

若小球的两个分运动中：这是一种一般的情况。解决的方法还是运动的合成，看下面推导：

水平方向位移：

从中解出时间：

竖直方向的位移：

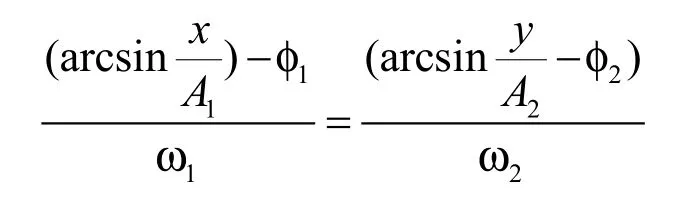
对方程变形：

解得：

很显然y和x的关系，并不是初等函数。我们不能直接看出小球运动的轨迹。解决问题的方法有两个：

（1）采用描点法画出函数图像，点越多图像越准确

（2）用实验的方法：掏空小球在其中装墨水或细沙，小球振动的过程中自然会画出其运动图像。这是借用了描简谐运动图像的方法。

（3）注意：上述函数关系式x和y的取值范围：

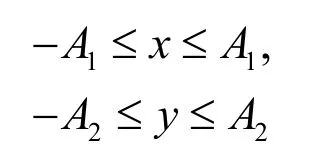
（4）可以推断：小球的运动轨迹将和角速度、振幅、初相位有关。对应这些物理量不同的值会有不同的图像。