简单齿轮的可靠性分析与研究

陆蕊

（江苏省淮安技师学院，江苏 淮安 223001）

0 引言

齿轮机构具有传动效率高、结构紧凑、传动平稳等优点，因此被广泛地应用于各类机器设备上，尤其是在重载传动方面，齿轮传动机构更是占据着举足轻重的地位。齿轮是机械中泛应用的传动零件之一，它具有功率范围大、传动效率高、传动比准确、使用寿命长等特点。但从零件失效的情况来看，齿轮也是最容易出故障的零件之一。数据统计表明[1]，在各种机械故障中，齿轮失效就占总数的60%以上。随着科学技术飞速发展，机械工业也发生着日新月异的变化，特别是近几十年来机电一体化产品的广泛应用，使得人们对齿轮的动态性能提出了更高的要求。非线性动力学、振动、噪声及其控制已成为当前国际科技界研究得非常活跃的前沿课题之一。与此同时，传统的静态设计方法也逐渐不能适应设计和运行的要求，而新兴的动态设计方法越来越被认同和采用。

如果齿轮结构的非标准设计不合理，其动态性能存在问题，在工作过程中会产生较大的振动和噪声，并会影响其工作精度和可靠性。齿轮的固有特性对其动力响应也有很大影响，动力响应是固有特性与激振力作用的综合表现。因此，对齿轮进行有限元模态分析，确定其固有频率和固有振型，避免系统工作时发生共振和出现有害振型，而目还可以找出齿轮的薄弱环节，可以为进一步进行齿轮的动力修改、噪声控制和优化设计奠定基础。

齿轮在工作时，在内部和外部激励下将发生机械振动，整个振动系统一般包括固有频率和振型等特性，它是系统的动态特性之一，对系统的动态响应、动载荷的产生与传递以及系统振动的形式等都具有重要的影响。此外，固有特性还是用振型叠加法求解系统响应的基础。然而，在齿轮的设计阶段，往往很难得到齿轮固有特性的实验数据，只能通过理论计算得到进行动力学分析的参数，目前最好的方法是有限元分析法。

运用有限元法分析齿轮的固有振动特性，通过有限元分析软件ANSYS分析了齿轮的各阶模态，得到了其低阶固有频率和对应主振型，其分析方法和所得结果可为直齿圆柱齿轮的动态设计提供参考，同时也为齿轮系统的故障诊断提供了一种方法。

1 有限元法与ANSYS软件

有限元法是一种高效能、常用的计算方法。有限元法在早期是以变分原理为基础发展起来的，所以它广泛地应用于以拉普拉斯方程和泊松方程所描述的各类物理场中（这类场与泛函的极值问题有着紧密的联系）[2-5]。有限元分析技术是最重要的工程分析技术之一。它广泛应用于弹塑性力学、断裂力学、流体力学、热传导等领域。有限元方法是60年代以来发展起来的新的数值计算方法，是计算机时代的产物。虽然有限元的概念早在40年代就有人提出，但由于当时计算机尚未出现，它并未受到人们的重视。随着计算机技术的发展，有限元法在各个工程领域中不断得到深入应用，现已遍及宇航工业、核工业、机电、化工、建筑、海洋等工业，是机械产品动、静、热特性分析的重要手段。

以ANSYS为代表的工程数值模拟软件，即有限元分析软件，具有功能比较强大、操作方便、硬件适应性较好等优点，并且不断吸取计算方法和计算机技术的最新进展，将有限元分析、计算机图形学、优化技术组合，己成为解决现代工程问题不可缺少的有力工具，也是本文的主要建模和分析处理工具。软件主要包括三个部分：前处理模块、分析计算模块和后处理模块。前处理模块提供了一个强大的实体建模及网格划分工具，用户可以方便地构造有限元模型。分析计算模块包括结构分析(可进行线性、非线性、高度非线性分析、接触分析等)、流体动力分析、热分析、电磁场分析、压电分析以及多物理场分析等，可模拟多种物理介质的相互作用，具有灵敏度分析及优化分析能力。后处理模块可将计算结果以彩色等值线显示、梯度显示、矢量显示、粒子流显示、立体切片显示、透明及半透明显示等图形方式显示出来，也可将计算结果以图表、曲线形式显示或输出。

2 齿轮的模态分析

模态分析是研究结构动力特性一种近代方法，是系统辨别方法在工程振动领域中的应用。模态是机械结构的固有振动特性，每一个模态具有特定的固有频率、阻尼比和模态振型。如果通过模态分析方法搞清楚了结构物在某一易受影响的频率范围内各阶主要模态的特性，就可能预言结构在此频段内在外部或内部各种振源作用下实际振动响应[6-9]。因此，模态分析是结构动态设计及设备的故障诊断的重要方法。

2.1 齿轮模型的建立

渐开线标准直齿圆柱齿轮是日常生活中应用最为广泛的齿轮之一，它具有结构简单、加工方便等特点。渐开线是由一条线段绕齿轮基圆旋转形成的曲线，其形成过程如下图2-1所示：

首先运用ANSYS数值软件画出齿轮的外部轮廓线，考虑实际齿轮尺寸，用ANSYS的Scale命令对所画轮廓进行0.003倍的缩小，生成齿轮轮廓线如图2-2所示。考虑到齿轮的立体模型，在拉伸处理时将其分为三个部分，分别对齿轮轮廓进行厚度为0.01、0.02和0.01的拉伸，经过处理后得到齿轮的ANSYS模型如图2-3所示。

另外，如图2-4所示为划分网格后的齿轮模型图。

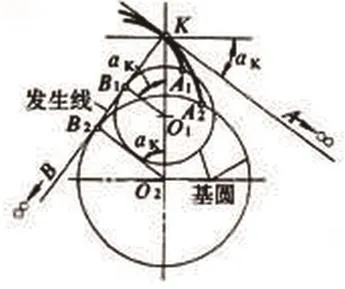
图2-1 渐开线的形成过程Fig 2-1 Forming process of involute

图2-2 齿轮外部轮廓线 Fig 2-2 External contour line of gear

图2-3 齿轮ANSYS模型Fig 2-3 ANSYS model of gear

图2-4 划分网格后的齿轮模型Fig 2-4 Gear model after grid dividing

2.2 模态分析

对齿轮进行模态分析的目的是求出齿轮各阶固有频率及其对应主振型，因此不需对模型加载，只需对其进行自由度约束，即约束齿轮的内孔圆柱面。指定模态提取方法为Block Lancws(分块兰索斯法)，设定模态提取阶数为15，即分析齿轮的前15阶固有频率。

表2-1 各阶固有频率Tab 2-1 Natural frequencies of each level

这里分别选取第1阶、5阶、10阶和15阶主振型齿轮模型模态分析图如下：

图2-6 主振型齿轮模型模态分析图Fig 2-6 Modal analysis diagram of main mode gear model

随后分别取不同厚度参数（0.05和0.06）重复上述分析过程，做进一步比较分析，得出三种不同厚度时的模态分析结果。将结果汇总后绘制各自各阶主振型的频率变化曲线如图2-5所示。

图2-5 三种厚度时齿轮的前15阶固有频率曲线Fig 2-5 The first 15 level natural frequency curves of gears with three kinds of thickness

3 结论

通过ANSYS软件建立了齿轮的三维有限元模型，对齿轮进行了有限元动力学模态分析，求出了齿轮的低阶固有频率和对应的主振型。通过对结果的分析可以得出：增加齿轮的厚度会使齿轮的固有频率发生，这与厚度增加后齿轮的刚度矩阵和质量矩阵的变化有关；通过图2-5可以发现第7、8、11、12阶的固有频率变化率较大，其对应的主振型均为扭振；且改变齿轮厚度后，会对齿轮的扭振产生相对较大的影响[10]。另外，当固有频率相同或相近时，对应的主振型也相同，但是其表现形式（振动方向）不同。

进一步得出结论：为了避免齿轮坐在的传动系统发生共振现象，应使外界激励响应的频率避开齿轮的固有频率。

[1] 叶友东, 周哲波. 基于ANSYS直齿圆柱齿轮有限元模态分析[J]. 机械传动, 2006, 30(5):63-65.YE You-dong, ZHOU Zhe-bo. Finite Element Modal Analysis of Spur Gear Based on ANSYS, [J].Mechanical Drive, 2006, 30 (5): 63-65.

[2] 李景涌. 有限元法[M]. 北京邮电学院出版社, 1999.LI Jing-yong. Finite Element Method [M]., Beijing Post and Telecommunication College Press, 1999.

[3] 商跃进.有限元原理与ANSYS应用指南[M].清华大学出版社.2005,6: 8.SHANG Yue-jin. Principles of Finite Element and ANSYS Application Guide [M]. Tsinghua University Press.2005,6: 8

[4] 殷祥超. 振动理论与测试技术[M]. 中国矿业大学出版社, 2007.YIN Xiang-chao. Vibration Theory and Testing Technology [M]. China University of Mining and Technology Press, 2007.

[5] 李常义,潘存云.基于ANSYS的渐开线圆柱齿轮参数化几何造型技术研究[J].机工程,2004, 21(9): 35.LI Chang-yi, PAN Cun-yun. Research on Involute Cylindrical Gear Parameterized Geometric Modeling Technology Based on ANSYS [J].Machanical Engineering,2004, 21(9): 35

[6] 李润方,王建军.齿轮系统动力学-振动、冲击、噪声,北京,科学出版社,1997.LI Run-fang, WANG Jian-jun. Gear System Dynamics - Vibration, Impact and Noise. Beijing Science Press, 1997.

[7] 王光建,熊正清.基于ANSYS的双螺旋副斜齿轮强度分析[J].新型工业化,2013,3(09):47-52.WANG Guang-jian, XIONG Zheng-qing. Analysis of Double Spiral Helical Gear Strength Based on ANSYS, [J]. New Industrialization 2013,3(09): 47-52.

[8] 刘哲, 陈定方, 陆忠华. 基于ANSYS的渐开线齿轮建模和有限元分析[J]. 湖北工业大学学报, 2008, 23(2):35-37.LIU Zhe, CHEN Ding-fang, LU Zhong-hua. Modeling and Finite Element Analysis of Involute Gear Based on ANSYS [J]. Journal of Hubei University of Technology, 2008, 23 (2): 35-37.

[9] 包家汉, 张玉华, 薛家国. 基于 ANSYS的齿轮参数化建模及其应用[J]. 安徽工业大学学报(自然科学版), 2005, 22(1):35-38.BAO Jia-han, ZHANG Yu-hua, XUE Jia-guo. Parameterized Modeling and Application of Gear Based on ANSYS[J]. Journal of Anhui University of Technology (NATURAL SCIENCE EDITION), 2005, 22 (1): 35-38.

[10] 杨富春.跨接双联斜齿轮非线性振动及功率分流特性研究[J].新型工业化,2014,4(10):53-61.YANG Fu-chun. Research on Nonlinear Vibration and Power Split Characteristics of Crossed Double Helical Gears [J]. Journal of New Industrialization, 2014,4 (10): 53-61.