一种基于在线遗传PID算法的分布式计算结构＊

梁达平 ，坚徳毅 ，赵兴彦 ，杜海峰

（1.天水师范学院 电信与电气工程学院，甘肃天水741000；2.天水电气传动研究所有限责任公司，甘肃天水741020；3.大型电气传动系统与装备技术国家重点实验室，甘肃天水741020）

1 引言

自适应在线遗传PID算法不仅具有传统遗传算法不受限于初始条件选择精准度、能够搜索系统全局最优解的优点，而且其自适应性可以更快地淘汰掉较差个体使算法的收敛效率更高。同时，它的在线模式可以在切分的每个采样时间间隔中更多次地获取设备当前状态，从而能够及时调节PID参数，提高了系统的鲁棒性，因此这种混合型遗传算法特别适用于实时性要求较高的工业控制设备中。

当然这种算法也存在需要改进之处，由于在线算法需要在每个较短的采样时间内完成一轮PID参数寻优，因此每一轮在线计算一般不能超过20代，这就极大地限制了每一次寻优的效果，基本上每一轮采样都只能寻找到较优解，而不能完全收敛于全局最优解，需要依靠反复多轮次计算，渐近式达到控制目标，对于设备的控制效果是有一定影响的。为了解决如何在较短的采样周期内获得更多计算次数的瓶颈问题，可以使用并行计算的思维，用多台联网控制器同时进行遗传计算以空间换取时间，这就是所谓分布式计算模式，即通过构建主从式网络拓朴实现多点并行计算，各子节点完成计算后将结果回传至主节点进行汇总分析在相同的采样周期内获得更多的样本个体，缩短寻优时间。

由于单控制器设备计算能力的物理限制，遗传算法这种优秀的无差别寻优方法在工业PID控制中始终不是主流算法。另一方面，如果将传统分布式结构引入遗传算法需要在硬件方面建立客户端-服务器模式，设备的控制器会由一个增加到多个，这就造成了设备制造成本的大幅上升，与通过算法计算提速所获取的收益不成正比，因此该方案的可行性不高，相应的这方面研究文献也比较少，只能从其它技术领域的类似研究中加以借鉴。例如，文献［1］将遗传优化算法与流体动力学分析方法相结合进行气动优化设计，形成了完整的设计方法，并通过该方法进行了翼型气动优化设计，实验结果表明该方法提高了设计质量与效率。文献［2］介绍了遗传算法与分布式计算的定义及关系，论述了采用分布式遗传算法解决板材套料问题的优势，并提出了基于分布式计算架构的板材套料优化计算模式和方法。文献［3］提出了一种利用遗传算法的分布式数据挖掘计算架构-MapReduce，通过MapReduce获得了较好的分布式计算平台，充分实现了遗传算法的全局最优解搜索，实验数据表明该计算架构能够提升海量数据挖掘的效果和性能。文献［4］为了解决遗传算法进行区域卫星星座优化设计中的计算量过大问题，提出了一种分布式计算模型及相应的计算方法，实验表明提高了计算效率，该方法也可应用到其它领域。文献［5］利用改进型分布式遗传算法求解多约束条件下移动Agent迁移策略的最优解，将Cascade模型与分布式遗传算法结合，通过在迁移算子中设计一个中心监控器观察子种群进化过程，并对个体选择和子种群大小进行调整，提高寻优速度。实验数据表明，该算法在计算的快速性和准确性方面取得较大提高。

从以上文献资料中可以看出，第一，将分布式计算模式应用于遗传算法中，的确可以提高遗传计算的速度，更快地收敛于最优解。第二，构建传统分布式计算模式时主要采用了两种作法，一种是物理上的多机分布架构，需要增加多台客户端以及联网设备的投入，对于单台工业设备来说成本提高的太多，甚至超过设备本身的成本，这显然是不可行的。另一种做法是在单台控制器上采用多节点仿真的模式，构造虚拟的分布式计算结构，这种方式仅仅能够将单控制器的计算能力充分利用起来，但工业设备的控制器一般来说其计算能力是有限的，所以仿真分布式计算结构在计算性能提升方面无法产生明显的效果。综上所述，要建立适合工业控制设备的分布式遗传计算模式，需要在保持计算效率的前提下，在算法的分布性、硬件结构的低成本化和安装体积最小化等方面满足生产实际的要求。

2 自适应在线遗传算法的PID整定原理

为了提高工业控制设备的动态响应特性，将传统遗传算法计算周期较长的寻优计算改进为在线计算模式，即将采样时间切分为一个个较短的时间片（例如，0.1s），在每个时间片内进行一轮完整的遗传计算并对设备参数进行校正，然后再次采集当前设备状态参数，并根据参数值进行新一轮的遗传计算，这样就可以更加快速地掌握设备最新状态，提高控制的实时性。另外，通过自适应策略解决不同设备个体由于难以避免的机械结构误差、参数设置不同、生产产品不同所带来的设备生产环境差异性问题，从而使设备控制系统具备更强的鲁棒性。例如，利用该算法我们成功地解决了IC（集成电路）芯片烘箱在温度控制中因腔体均匀性差异导致调节效率低的问题。

该算法的具体计算流程如下：

设备PID控制系统的方块图如图1所示，在前向通道配置PID控制器，控制器对应的3个PID参数为KP、TI、TD；G（s）表示设备被控制对象的传递函数。

图1 PID控制系统方块图

为了便于计算和分析3个PID环节参数，需要将PID控制器的传递函数作等效变换，如公式（1）所示：

其中 KI＝KP/TI，KD＝KPTD。第一步，根据生产经验选定设备PID控制器3个参数的取值区间。设KP∈［p1，p2］，KI∈［i1，i2］，KD∈［d1，d2］。

第二步，遗传计算选取的样本个体总数设为n，由于是在线算法，需设定采样周期，周期设为Ta（周期的时长一般比较短，例如0.1s），每个采样周期内的计算轮数设为m代（为了获得较好的实时性，通常要小于20代）。

第三步，设计系统的目标函数和适应度函数。对于大多数工业控制设备来说，输出超调对于产品质量的损害是十分严重的，因此需要控制输出响应曲线上升到目标值附近时不要产生较大幅度的振荡或毛刺，为了抑制输出超调的产生，达到理想的过渡性能，可以将个体i的最小目标函数设计为误差变化率与位置误差加权之和，如公式（2）和公式（3）所示，其中k1，k2表示各自所占的权重。适应度函数与最小目标函数为倒数关系。

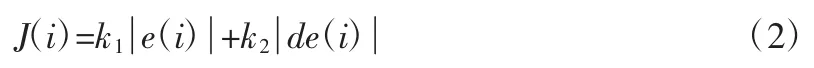
当系统出现超调时，公式（2）由公式（3）替代，以保证造成超调的较差个体被淘汰：

这样就将自适应性引入算法中，可以根据不同设备或同一设备不同环境状态进行PID参数自适应调节。

第四步，选用实数编码方式，建立种群的样本个体。每个个体产生的计算方法如公式（4）（5）（6）所示：

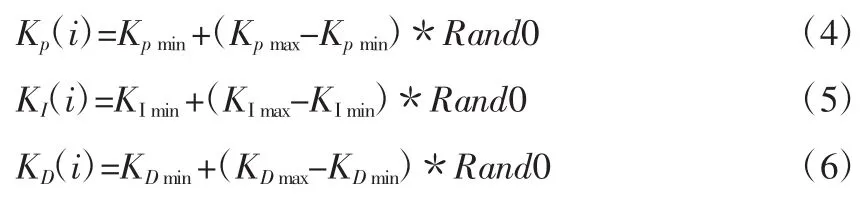
第五步，交叉操作按照Pc＝0.9的交叉概率进行；变异操作按照 Pmi＝0.2-i×0.01/n（i＝1，2…n）的变异概率进行。

在每个采样周期内，重复运行第二步到第五步。

3 分层式遗传算法改进的原理

如前所述，自适应在线遗传PID算法虽然能够提高设备控制性能，达到指标要求，但上述算法是基于单控制器设计的，并不适用于分布式计算模式。因此需要对算法做进一步改进，使其具有多点并行计算寻优的特点，为此我们引入了分层方式［6］。下面介绍一下分层式遗传算法的计算原理：

针对被调节参数随机生成 N＊n 个样本（N＞＝2，n＞＝2），然后将其分成N个平行种群，每个种群含有n个初始样本，在种群内进行各自独立的遗传计算。N个平行种群在设置时，可以引入完全不同的性能侧重，这样就可以在后期计算阶段产生出更多类型的优良个体。每当种群内的遗传计算运行到一定的代数时，就将这N个种群的遗传样本数据内容保存到二维数组 R［1..N，1..n］中，将 N 个种群的平均适应度保存到数组A［1..N］中。根据A数组中的N个平均适应度值，对R数组中保存的当前各个结果种群进行选择操作。当 R［i，1..N］与 R［j，1..N］被随机匹配在一对时，按照预先（或随机）设定的权重进行对应重组，完成组间交叉。同时，也在每个种群按照预设概率将少量随机生成的新个体替换掉 R［1..N，1..n］中随机选定的个体。以上平行种群之间的操作被称为高层操作，各种群内部的独立操作被称为低层操作，均按照一定的预设轮数循环执行。分层方式可以更大范围的搜索最优解，有效避免过早陷入局部最优；缺点是搜索个体数相对更多、计算量比较大，对于单控制器设备来说来会影响控制的实时性，但是非常适用于分布式计算结构。

分层式遗传计算流程如图2所示。

第一步，选择操作。根据每组各自的平均适应度值，对数组R中保存的组内所有个体进行筛选工作，将适应度值低于平均适应度的个体淘汰掉，高于平均适应度的个体不仅保留，还要进行复制并填充淘汰掉的个体所留下的位置。

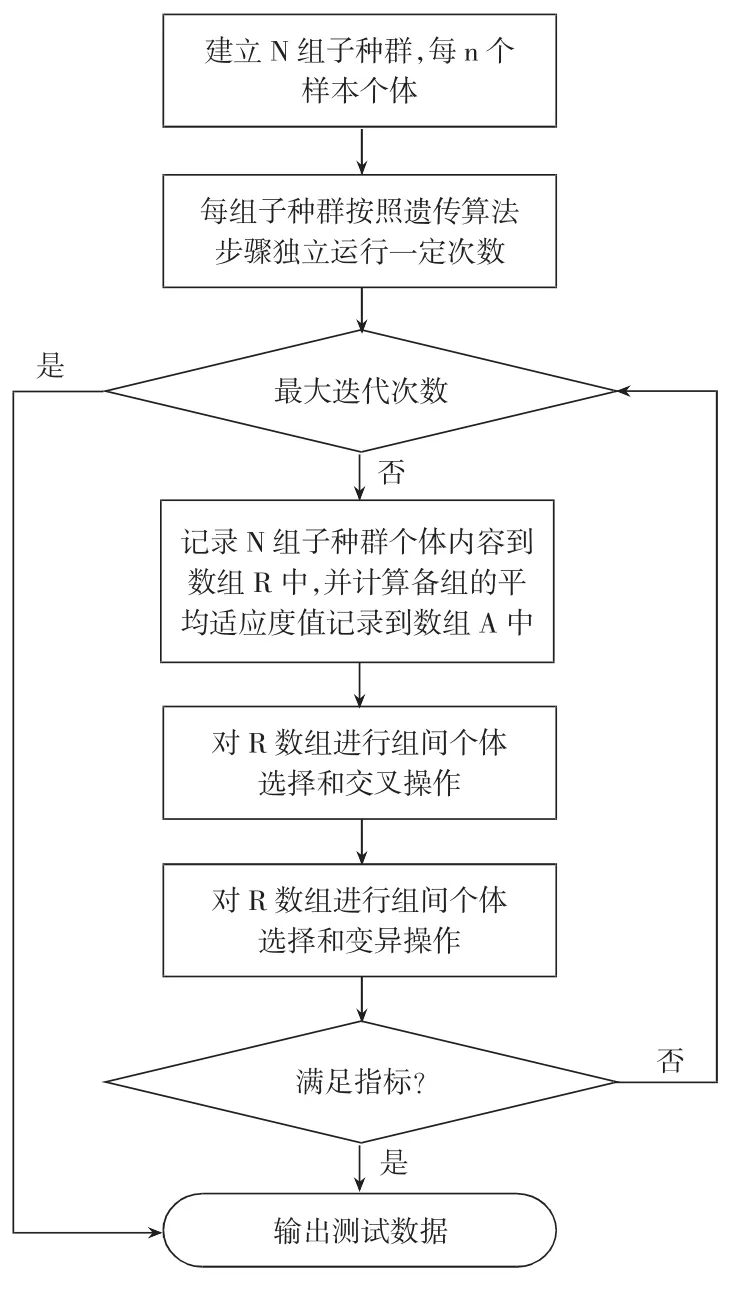
图2 分组式遗传算法运行流程图

第二步，交叉操作。按照预设的交叉概率Pc将组间的个体随机跨组匹配，然后按照预设的权重进行加权交叉操作，即 Rix＝α×Rix＋（1-α）×Riy，Riy＝（1-α）×Rix＋α×Riy。其中，Rix和 Riy分别表示选中的两个个体，α表示预设的交叉权重值。

第三步，变异操作。按照预设的变异概率Pm在组间进行随机生成操作将选中的个体替换掉，即 Rix＝（Rimax＋Rimin）/2＋（Rimax-Rimin）×（Rand（）-0.5）。其中，Rix表示选中的个体，Rimax和Rimin表示该组子种群取值区间的最大值和最小值，Rand（）表示（0，1）区间随机函数。

以上步骤每隔一个预设间隔就重复运行一次。N组平行种群可以在各自组内进行完全独立的自适应在线遗传计算，寻找各自的最优解（低层组内操作）；然后通过上述步骤完成高层组间操作。从而在相同的时间内利用多组遗传计算扩大了搜索的寻优范围，不仅避免了陷入局部最优问题，也提高了搜索效率。更为重要的是这种方式能够充分发挥出分布式计算的优势，可将每一个或几个平行种群组的低层遗传计算分别放在每一个计算节点上，这样各组的计算就与分布式并行结构完全结合在一起，在每一个采样时间结束时，将各子节点的计算结果汇总到主节点进行高层的组间遗传计算，得到优化结果。

4 分布式计算的硬件实现方案

分布式计算模式从逻辑结构上看，属于主从式网络拓朴，通过多个计算节点分布式独立展开并行计算，最后通过主节点汇总处理各子节点回传的数据得出最终计算结果。在物理实现上，常规的做法是采用多台PC机及网络通讯设备构建集群式计算网络。这种方式对于解决大数据分析、数据挖掘等高计算量、高成本需求类行业的问题是很有效的（如电商网站、移动及电信服务商等），但是对于单台成本较低、便于移动的工业控制设备来说，给每台设备都配置这样规模较大的网络架构，从经济投入到安装体积等方面考虑显然是很不现实的。因此，为了建立符合工业设备要求的分布式计算结构，我们提出了以下两种物理实现方案。

4.1 基于嵌入式多智能端的结构

为了降低采用分布式结构的设备制造成本并限制控制系统过大的体积，可以将各计算节点由PC机替换为嵌入式微控制器，这样既可以保证较高的计算性能，也大大缩小了控制系统所需的安装空间。如图3所示，各分控制器均为嵌入式微系统，与主控制器通过采用ModBus协议［7］的RS485物理总线连接，主控制器则可以选用较高性能的嵌入式微系统或体积较小的一体式PC机。

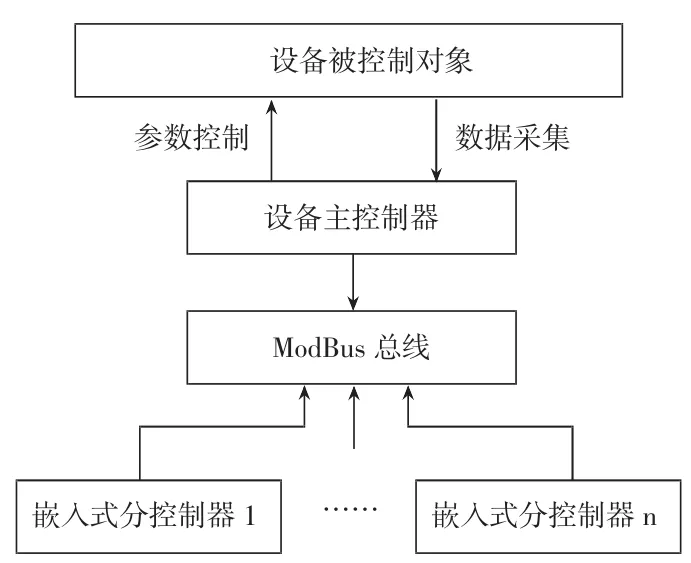
图3 嵌入式多智能端分布式计算结构

主控制器在每个采样周期中，首先采集设备相关状态参数的数据，然后通过RS485总线传送给所有分控制器，在每个分控制器上进行各自独立的遗传计算（低层计算），当采样周期结束时，各分控制器上传计算结果至主控制器，在主控制器中运行高层遗传算法得到本轮采样周期的参数最优解，并以PID控制方式对被控参数进行调节。

4.2 基于工业局域网模式的设备网络结构

对于大型制造企业来说，如果购买的工业控制设备数量较多，可以进一步考虑组成设备工业局域网，每一台设备作为一个子节点，并在上位端安装一台性能较强的主服务器作为主节点。如图4所示，在每轮采样周期开始时，各子节点处的工业设备将各自当前的状态参数通过以太网总线上传至主服务器，利用主服务器的超强计算能力进行多轮伪并行遗传计算，当采样周期结束时，服务器将计算结果回传给各设备端。

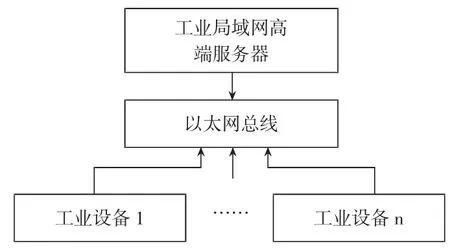
图4 工业局域网分布式计算结构

这种类似云端计算的局域网方式，既可以将多台单控制器设备整体升级为分布式计算模式，也可以在设备使用了前述的第一个方案后，通过本结构建立计算性能更强的三层式分层遗传算法控制结构，即主服务器层、各设备的主控制器层和分控制器层。

5 实验数据分析

5.1 被控制对象模型的辨识

根据大量实验分析和理论研究表明，大多数工业控制设备的系统环境都具有自衡的能力，其传递函数模型可采用延迟环节和惯性环节的乘积来近似描述，如公式（7）所示：

其中：KC为系统放大系数，TC为设备时间常数，τ为被控参数变化的时间常数。

这种有自衡能力的一阶惯性控制装置在进行系统参数辨识时，通常采用反应曲线法、衰减曲线法或稳定边界法测算，综合考虑实验数据的采集难度和各方法的适用范围，这里使用反应曲线法［8］来计算系统模型所需参数。

下面，以曾经自主研发的IC芯片无氧化烘箱为例，说明利用反应曲线法对被控系统进行辨识的过程。首先，由于多数产品所需工作温度在175℃左右，因此可以将烘箱腔体内的初始温度设置为165℃，加热器的目标温度设为175℃，通过每30s间隔进行一次温度采样，获取温度变化过程的数据点。利用MatLab软件中的6阶多项式拟合函数［9］对这些数据点进行曲线平滑处理以提高处理精度，最终得到烘箱内环境温度的飞升曲线如图5所示。过曲线的拐点P画切线和辅助线，可估算出公式（7）所需参数的具体数值，其中 KC＝0.9，TC＝640，τ＝160。

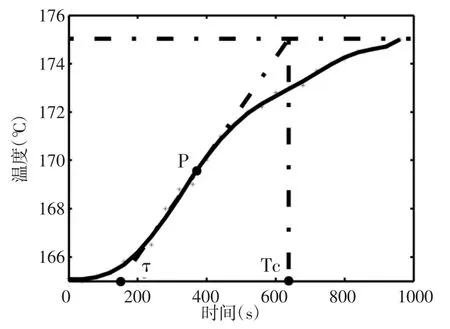
图5 烘箱腔体温度飞升曲线图

5.2 算法性能比较分析

为了兼顾算法模型的普适性和有效性，算法测试对象分别选择为5.1节中根据公式（7）推导的设备仿真模型和实际的IC芯片烘箱温控系统，分两次进行单机算法与分布式算法的性能对比分析，从而得到更加客观准确的评价结论。

在分别采用两种遗传算法的温控仿真系统输入端引入阶跃信号（初始为165℃，阶跃目标为175℃），每隔30s采集一次控制器响应输出数据，并经过MatLab拟合处理后得到响应曲线如图6所示。可以看出两者在上升速度与超调量的平衡处理方面表现都很好，在保证较高快速性的前提下基本没有出现明显的超调，这对于生产过程控制来说是最重要的指标之一，因为一个不起眼的毛刺信号可能就会造成大批产品在生产过程中被损坏。在稳态误差方面两者的表现也很好，进入稳态后实际曲线能够与目标曲线重合，完全实现了恒温控制的核心功能。此外，在良好的动态与稳态性能基础上，分布式算法响应曲线还体现出更好的实时性和计算优势，在初始上升速度方面明显优于单控制器设备，体现出更强更广泛的适应性，可以用于要求更加严格的工业生产中。

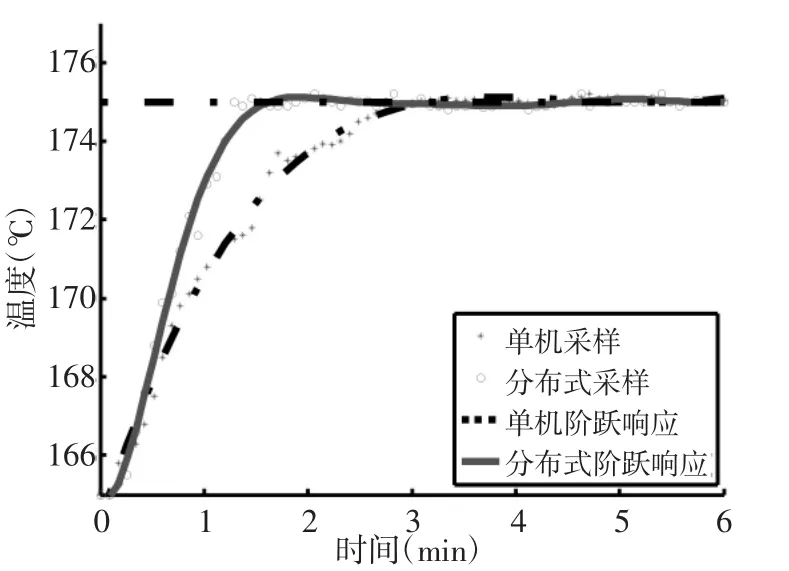
图6 基于仿真对象的两种阶跃响应曲线对比

同样的，在分别采用两种遗传算法的IC芯片烘箱温控系统输入端引入阶跃信号（初始为98℃，阶跃目标为175℃），采集并处理设备控制器实际输出响应曲线如图7所示。可以看到除了两种算法均能满足烘箱的生产要求之外，分布式控制器快速性能更好，初始调节时间只有不到10分钟，而单控制器设备需要20分钟左右。

显然，引入分布式计算模式后，系统阶跃响应曲线的上升时间、调节时间等快速性指标进一步获得提升，突破了单控制器计算的物理限制。此外，原始采集数据点的坐标分布也反映出，相比于单机系统，分布式系统的稳态误差趋于0，抗干扰性和鲁棒性均得到同步提高。

6 结束语

本文采用分层模式对自适应在线遗传PID算法进行改进，与主从式网络架构相结合构建出符合工业生产实际的分布式计算结构，并将其引入设备控制系统，在成本和安装体积基本不变的前提下，突破了采用单控制器时在线算法的计算瓶颈。通过对优化前后两种算法模型的实验数据对比表明，分布式结构提高了原算法的搜索速度、扩大了搜索范围；采用分布式遗传PID控制方案的设备综合性能要远优于采用传统PID方案的设备，其被控参数调节速率明显提高，具有良好的动态特性和鲁棒性。该模型可广泛应用于各类嵌入式工业控制设备的PID控制系统中。

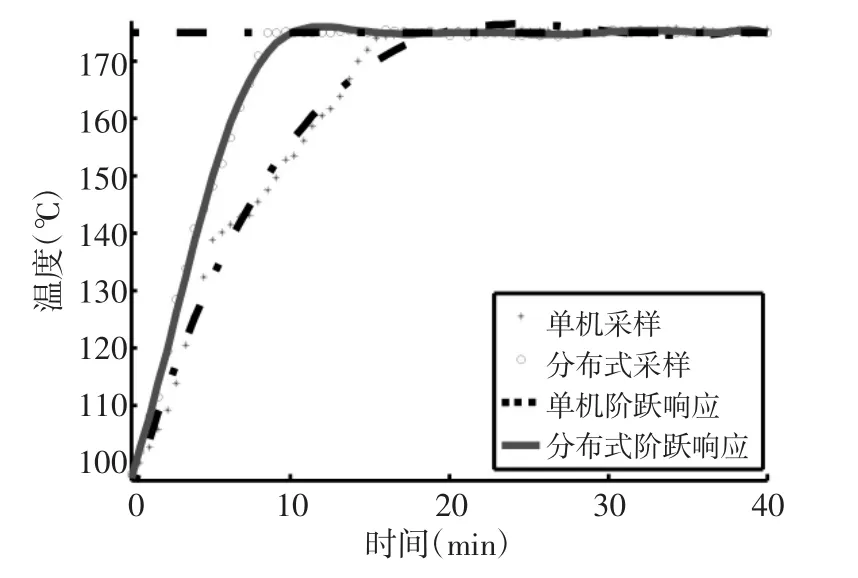
图7 基于实际设备的两种阶跃响应曲线对比