双腔光力学系统中输出光场纠缠特性的研究∗

张秀龙 鲍倩倩 杨明珠 田雪松

1)(东北石油大学电子科学学院,大庆 163318)

2)(辽宁大学物理学院,沈阳 110036)

3)(黑龙江科技大学理学院,哈尔滨 150001)

1 引 言

量子纠缠是量子物理区别于经典物理的最显著特征之一.它不但可用于验证可观测量之间量子关联的非局域性,而且在量子信息处理和量子通信等领域有极其重要的应用价值.自薛定谔等提出量子纠缠以来,量子纠缠就引起了人们极大的兴趣.人们在理论上和实验上对宏观物体之间的量子纠缠都做了广泛研究,比如在原子系综之间的纠缠[1,2]以及超导量子比特之间的纠缠[3−6].近年来由于纳米技术的进步,使腔光力学得到了快速发展[7−10].最近,腔光力学系统中的量子纠缠引起了越来越多的关注,因为腔光力学系统中的光辐射压力可以使系统中的各个子系统之间产生量子纠缠.例如,在理论上对光力学系统中谐振子之间的纠缠[11−14]、不同光模之间的纠缠[15−26]以及光模与谐振子之间的纠缠[27−35]都做了广泛研究,而在最近一个实验中实现了谐振子与微波场之间的量子纠缠[36].

本文研究了左右两个光腔与中间一个力学振子耦合的光力系统中输出光场之间的量子纠缠的性质,此系统中,在参数放大相互作用和劈裂相互作用的共同作用下,使左右两腔中的光模之间产生量子纠缠,从而使经过滤波器后的输出光场之间也会产生量子纠缠.研究发现,力学振子的弛豫速率、滤波器的带宽以及非相等耦合(左右两腔的有效光力耦合常数G1与G2不相等)都对输出光场之间的量子纠缠大小有着显著的影响.这些研究结果有望应用于在光力系统中实现量子态转换、量子隐形传态等量子信息处理过程.

2 理论模型与主要公式

我们研究了一个双腔光力学系统,如图1所示,左右两个光学腔与中间一个力学振子相耦合;分别表示光学腔i和力学振子的湮灭算符(本征频率);κi和γ分别表示光腔i和力学振子的弛豫速率.驱动场Hd从左右两侧射入并驱动腔模ωi,则系统的哈密顿量可写为

其中gi为光学腔i与力学振子之间的耦合常数.如果用红边带激光(ωd1=ω1−ωm)和蓝边带激光(ωd2=ω2+ωm)分别驱动腔1和腔2,通过标准的线性化方法,在相对系统自由哈密顿量做旋转以及在旋波近似下,则系统哈密顿量变为

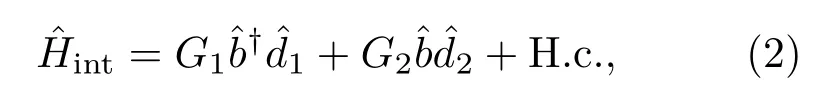
由系统哈密顿量(2)可以得出系统算符的海森伯-郎之万运动方程:

其中分别为力学振子和光腔的输入热噪声算符,其关联函数分别为Ni分别为力学振子和光学腔的平均热占有数.本文主要研究在系统参数满足κi≫γ和的条件下,滤波器带宽σ、力学振子弛豫速率γ以及非相等耦合G2G2时,系统总是稳定的[21,24].

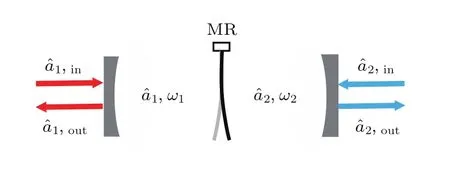
图1 双腔光力学系统输出光场示意图Fig.1. Sketch of the output light fields in a doublecavity optomechanical system.

本文采用对数负性[38,39]的方法来数值计算两个输出光场之间的量子纠缠大小.经过滤波器之后的输出光场可以表示为

为简单起见,采用方形滤波函数来输出光场,即

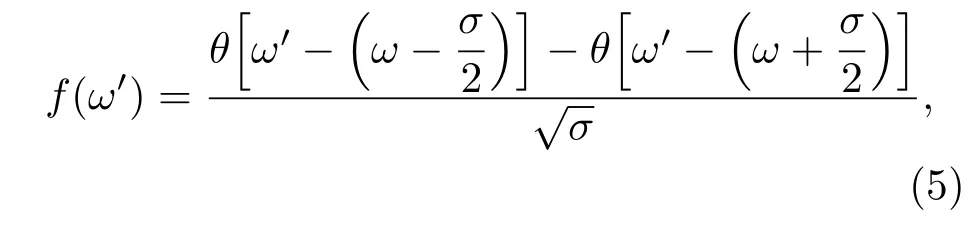
其中θ[ω]为阶跃函数,σ为输出光场的带宽,ω为输出光场的中心频率.则经过此方形滤波函数的输出光场可以表示为

其中,τi为光场从光腔ωi的输出时间,本文研究从两光学腔同时输出的光场之间的纠缠,所以可取τ1=τ2=0.用对数负性来计算输出光场之间的量子纠缠度,其定义为

其中

和

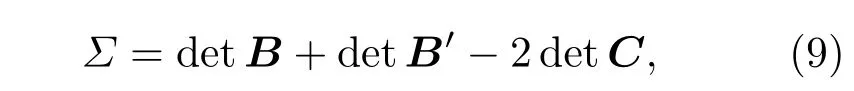
以及4×4关联矩阵V的定义为⟩,其中,且.2×2矩阵B,B′和C与关联矩阵V的关系为

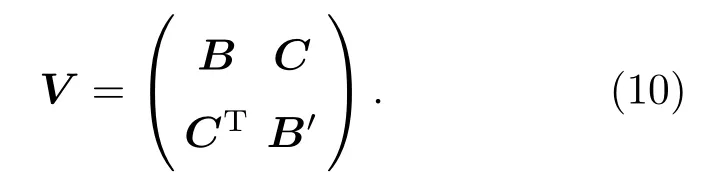
3 输出光场之间的纠缠性质

根据对数负性(9)式来分别讨论力学振子的弛豫速率γ、滤波器带宽σ以及非相等耦合G1>G2对输出光场之间纠缠的影响.

首先研究力学振子的弛豫速率γ对纠缠的影响,这里主要讨论强耦合情况(G>κ),并取参数G1=G2=G=5×105,κ1=κ2=κ=105以及σ→0.带宽σ→0,此时输出光场为单色平面波,滤波器的中心频率ω即为输出光场的频率.图2给出了在力学振子弛豫速率γ不同取值下,即γ=1(红色实线),γ=102(蓝色虚线),γ=104(绿色点线)时的输出光场之间纠缠En随着滤波器中心频率ω/κ的变化曲线.从图2可知,在σ→0的条件下,当输出光场的中心频率与光学腔共振时(在旋转参考系下,共振时ω=0),两个输出光场之间的纠缠最大,纠缠随着中心频率ω的增加不断减小,并且有En(ω)=En(−ω).通过计算可知,在共振时纠缠,由此可以看出在输出光场中心频率与光学腔共振频率附近,力学振子的弛豫速率γ对输出光场之间的纠缠有着很大的影响,γ=1时,En(0)≈16.81,γ=102时,En(0)≈12.21,γ=104时,En(0)≈7.60.而当输出光场的中心频率远离光学腔的共振频率时,力学振子的弛豫速率γ对纠缠的影响逐渐减小.对于弱耦合情况(G<κ),纠缠曲线形状与强耦合情况没有太大区别,只是纠缠数值相对较小,图2只给出了γ=102时的弱耦合纠缠曲线,见黑色实线,其他参数为:G1=G2=G=2×104,κ1=κ2=κ=105.

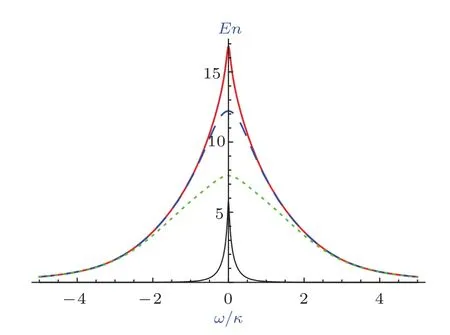
图2 在σ→0的条件下,力学振子弛豫速率γ取不同值时,输出光场之间纠缠En随着输出光场中心频率ω/κ的变化曲线 强耦合条件下(G=5κ=5×105),γ=1(红色实线),γ=102(蓝色虚线),γ=104(绿色点线);弱耦合条件下(G=κ/5=2×104),γ=102(黑色实线)Fig.2. Under the condition of σ → 0,the output entanglement En is plotted with the change of center frequency of output fields ω/κ for different mechanical decay γ:for strong coupling(G=5κ =5×105),γ =1(red solid line),γ=102(blue dashed line),γ=104(green dotted line);for weak coupling(G=κ/5=2×104),γ=102(black solid line).

由以上讨论可知,当σ→0时输出光场纠缠的最大值出现在共振处,即ω=0.然而接下来的讨论发现,滤波器半宽σ对输出光场纠缠产生重要的影响.当σ取有限值时,纠缠的最大值不再出现在ω=0的位置,相反在ω=0处,纠缠取局部最小值.在这里我们只讨论强耦合情况(弱耦合纠缠图形只是数值较小),并取参数γ=1,G=5κ=5×105(G1=G2=G,κ1=κ2=κ).通过计算可知,当输出光场中心频率ω满足时,. 图3给出了在滤波器带宽σ取不同值时输出光场纠缠En随着输出光场中心频率ω/κ的变化曲线:σ=103(红色虚线),σ=104(蓝色点线),σ=105(绿色实线).由图3可知,输出光场之间的纠缠En最大值出现在绝对值大于σ/2的某一中心频率处,而在范围内几乎为零,这是因为γ/σ≈0.这说明滤波器带宽σ对共振频率附近的纠缠有很强的抑制作用.输出纠缠的最大值也随着σ的增加不断降低.由公式可知,当半宽σ不为零时,可以通过提高力学振子的弛豫速率γ的方法来提高共振频率(ω=0)附近的输出光场纠缠大小.

图3 在滤波器带宽σ取不同值时,输出光场之间纠缠En随着输出光场中心频率ω/κ的变化曲线 σ=103(红色虚线),σ=104(蓝色点线),σ=105(绿色实线);其他参数 γ=1,G1=G2=G=5×105,κ1=κ2=κ=105Fig.3.The output entanglement En is plotted with the change of center frequency of output fields ω/κ for different filter bandwidth σ: σ =103(red dashed line),σ=104(blue dotted line),σ=105(green solid line).Other parameters:γ=1,G1=G2=G=5×105,κ1= κ2=κ =105.

最后讨论非相等耦合(G1>G2)对输出光场纠缠的影响,这里分强耦合和弱耦合两种情况讨论,参数取γ=1,σ=103,κ=105.强耦合情况下(G1=G=5×105>κ),图4给出了在G2/G1取不同值时输出纠缠En随着输出光场中心频率ω/κ的变化曲线:G2/G1=1(红色虚线);G2/G1=0.95(蓝色点线);G2/G1=0.90(黑色实线).当G2/G1=1时,由上面的讨论可知,滤波器带宽σ对ω=0附近的纠缠产生很强的抑制作用.但是如果采用非相等耦合,则可以有效抵制滤波器带宽σ对输出纠缠的抑制作用(见图4中的蓝色点线和黑色实线).由图4可知,与相等耦合时(红色虚线)在ω=0附近的输出纠缠相比,非相等耦合时的输出纠缠得到大幅提高,并在共振频率处取局部最大值,而且非相等耦合时输出光场纠缠会出现三个峰值.这是因为在强耦合条件下哈密顿量Hint的三个本征模发生劈裂[22].图5给出了在弱耦合时(G1=G=2×104<κ),在G2/G1取不同值时,输出纠缠En随着输出光场中心频率ω/κ的变化曲线:G2/G1=1(红色虚线);G2/G1=0.95(蓝色点线);G2/G1=0.90(黑色实线).由图5可见,在弱耦合时输出光场纠缠值比强耦合时小很多,由于是弱耦合,所以不会出现本征模劈裂现象,而输出纠缠却出现两个峰值,这是因为滤波器半宽σ对共振频率ω=0附近的输出纠缠En有很强的抑制作用,使本来不应该出现劈裂的现象出现了两个峰.

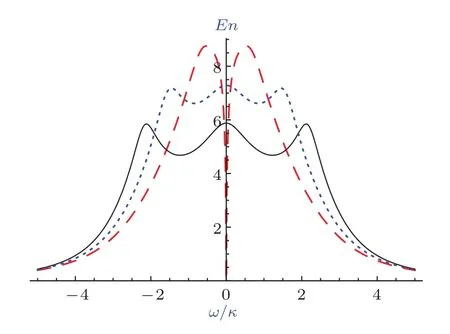
图4 在强耦合条件下,G2/G1取不同值时输出纠缠En随着输出光场中心频率ω/κ的变化曲线 G2/G1=1(红色虚线),G2/G1=0.95(蓝色点线),G2/G1=0.90(黑色实线);其他参数γ=1,σ=103,κ=105,G1=5κFig.4. With strong coupling,the output entanglement En is plotted with the change of center frequency of output fields ω/κ for different values of G2/G1:G2/G1=1(red dashed line),G2/G1=0.95(blue dotted line),G2/G1=0.90(black solid line).Other parameters:γ =1,σ =103,κ =105,G1=5κ.

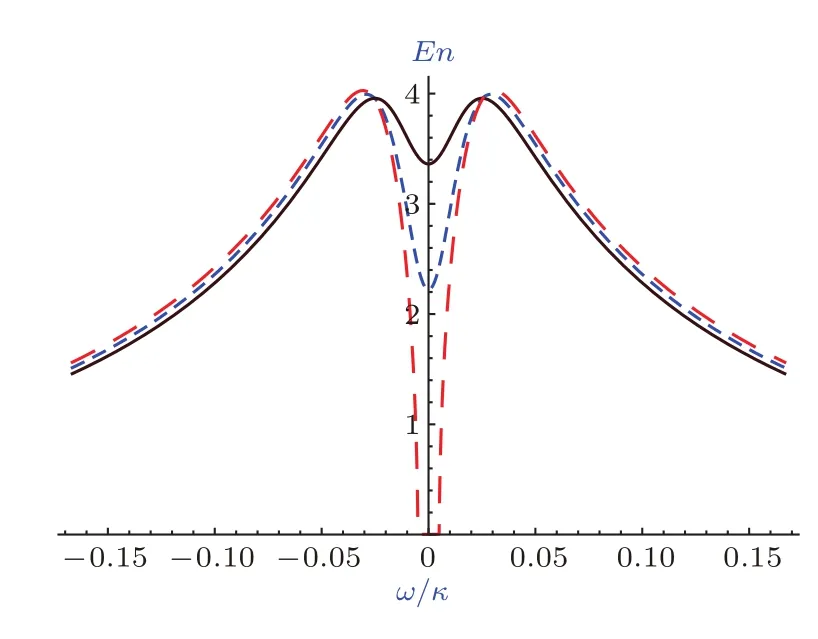
图5 在弱耦合条件下,G2/G1取不同值时输出纠缠En随着输出光场中心频率ω/κ的变化曲线 G2/G1=1(红色虚线),G2/G1=0.95(蓝色点线),G2/G1=0.90(黑色实线);其他参数γ=1,σ=103,κ=105,G1=κ/5Fig.5. With weak coupling,the output entanglement En is plotted with the change of center frequency of output fields ω/κ for different values of G2/G1:G2/G1=1(red dashed line),G2/G1=0.95(blue dotted line),G2/G1=0.90(black solid line).Other parameters:γ=1,σ=103,κ=105,G1=κ/5.

4 结 论

对双腔光力学系统中输出光场之间的纠缠性质进行了分析.研究发现,此系统中力学振子的弛豫速率γ和滤波器带宽σ的大小以及非相等耦合G1>G2条件对输出光场之间纠缠的大小都有着显著的影响,特别是在相等耦合时(G1=G2)和输出光场中心频率在光学腔本征频率附近时,滤波器带宽σ对纠缠有很强的抑制作用;但是如果采用非相等耦合,则可以有效抵制滤波器带宽的这种抑制作用;当系统在强耦合参数区域时,如果采用非相等耦合,则输出光场纠缠会出现三个峰值,这是因为此时系统的哈密顿量Hint的三个本征模发生劈裂;而对于弱耦合纠缠会出现两个峰值,这是因为滤波器半宽σ对共振频率ω=0附近的输出纠缠En有很强的抑制作用,使本来不应该出现劈裂的现象出现了两个峰.这些研究结果有望应用于光力系统中量子态转换、量子隐形传态等量子信息处理过程.

[1]Julsgaard B,Kozhekin A,Polzik E S 2001Nature413 400

[2]Krauter H,Muschik C A,Jensen K,Wasilewski W,Petersen J M,Cirac J I,Polzik E S 2011Phys.Rev.Lett.107 080503

[3]Berkley A J,Xu H,Ramos R C,Gubrud M A,Strauch F W,Johnson P R,Anderson J R,Dragt A J,Lobb C J,Wellstood F C 2003Science300 1548

[4]Neeley M,Bialczak R C,Lenander M,Lucero E,Mariantoni M,Sank D,Wang H,Weides M,Wenner J,Yin Y,Yamamoto T,Cleland A N,Martinis J M 2010Nature467 570

[5]DiCarlo L,Reed M,Sun L,Johnson B L,Chow J M,Gambetta J M,Frunzio L,Girvin S M,Devoret M H,Schoelkopf R J 2010Nature467 574

[6]Flurin E,Roch N,Mallet F,Devoret M H,Huard B 2012Phys.Rev.Lett.109 183901

[7]Aspelmeyer M,Kippenberg T J,Marquardt F 2014Rev.Mod.Phys.86 1391

[8]Chen X,Liu X W,Zhang K Y,Yuan C H,Zhang W P 2015Acta Phys.Sin.64 164211(in Chinese)[陈雪, 刘晓威,张可烨,袁春华,张卫平2015物理学报64 164211]

[9]Chen H J,Fang X W,Chen C Z,Li Y 2016Acta Phys.Sin.65 194205(in Chinese)[陈华俊,方贤文,陈昌兆,李洋2016物理学报65 194205]

[10]Yan X B,Yang L,Tian X D,Liu Y M,Zhang Y 2014Acta Phys.Sin.63 204201(in Chinese)[严晓波,杨柳,田雪冬,刘一谋,张岩2014物理学报63 204201]

[11]Bhattacharya M,Giscard P L,Meystre P 2008Phys.Rev.A77 030303

[12]Chen R X,Shen L T,Yang Z B,Wu H Z,Zheng S B 2014Phys.Rev.A89 023843

[13]Liao J Q,Wu Q Q,Nori F 2014Phys.Rev.A89 014302

[14]Yang C J,An J H,Yang W,Li Y 2015Phys.Rev.A92 062311

[15]Paternostro M,Vitali D,Gigan S,Kim M S,Brukner C,Eisert J,Aspelmeyer M 2007Phys.Rev.Lett.99 250401

[16]Wipf C,Corbitt T,Chen Y,Mavalvala N 2008New J.Phys.10 095017

[17]Genes C,Mari A,Tombesi P,Vitali D 2008Phys.Rev.A78 032316

[18]Barzanjeh Sh,Vitali D,Tombesi P,Milburn G J 2011Phys.Rev.A84 042342

[19]Barzanjeh Sh,Abdi M,Milburn G J,Tombesi P,Vitali D 2012Phys.Rev.Lett.109 130503

[20]Barzanjeh Sh,Pirandola S,Weedbrook C 2013Phys.Rev.A88 042331

[21]Wang Y D,Clerk A A 2013Phys.Rev.Lett.110 253601

[22]Tian L 2013Phys.Rev.Lett.110 233602

[23]Kuzyk M C,van Enk S J,Wang H 2013Phys.Rev.A88 062341

[24]Wang Y D,Chesi S Clerk A A 2015Phys.Rev.A91 013807

[25]Deng Z J,Habraken S J M,Marquardt F 2016New J.Phys.18 063022

[26]Deng Z J,Yan X B,Wang Y D,Wu C W 2016Phys.Rev.A93 033842

[27]Vitali D,Gigan S,Ferreira A,Böhm H R,Tombesi P,Guerreiro A,Vedral V,Zeilinger A,Aspelmeyer M 2007Phys.Rev.Lett.98 030405

[28]Hofer S G,Wieczorek W,Aspelmeyer M,Hammerer K 2011Phys.Rev.A84 052327

[29]Akram U,Munro W,Nemoto K,Milburn G J 2012Phys.Rev.A86 042306

[30]Sinha K,Lin S Y,Hu B L 2015Phys.Rev.A92 023852

[31]He Q Y,Ficek Z 2014Phys.Rev.A89 022332

[32]Kiesewetter S,He Q Y,Drummond P D,Reid M D 2014Phys.Rev.A90 043805

[33]He Q Y,Reid M D 2013Phys.Rev.A88 052121

[34]Wang M,Gong Q H,Ficek Z,He Q Y 2015Sci.Rep.5 12346

[35]Wang M,Gong Q H,Ficek Z,He Q Y 2014Phys.Rev.A90 023801

[36]Palomaki T A,Teufel J D,Simmonds R W,Lehnert K W 2013Science342 710

[37]DeJesus E X,Kaufman C 1987Phys.Rev.A35 5288

[38]Vidal G,Werner R F 2002Phys.Rev.A65 032314

[39]Plenio M B 2005Phys.Rev.Lett.95 090503