广义相对论的牛顿近似

(天津市南开区职工大学，天津 300102)

爱因斯坦的广义相对论是现代引力理论，是人类思想史的重大突破。从理论的高度而言，它理所当然应当能够涵盖传统的引力理论，即牛顿的万有引力定律。牛顿引力理论是在低速、静止状态下引力性质的必然体现，是经过严格的实验证明的。如果广义相对论运用到低速、静止状态下的情形时不能自动退化为万有引力定律，就不能体现广义相对论的正确性。因此，这一问题是十分重要的。本文准备就这一问题进行探讨。

一、静态引力场中能量—动量张量的表现形式

(1)

解爱因斯坦方程的关键是确定方程式右边的能量—动量四维张量，这个张量在不同的情况下会有不同的表现形式。在静态情况下的某一个孤立的引力源，其能量—动量四维张量的表现方式应当是这样的。

TAB=ρuAuB

(2)

在静态引力场中，由于

u0=C

uA=uB=0(当A或者B不等于0时，此时引力源没有速度或者速度可以忽略不计)

这样就有：

T00=ρu0u0=ρc2

(3)

T=g00T00=-T00=-ρc2

(4)

TAB=ρuAuB=0(除非A=B=0)

(5)

二、静态引力场中的爱因斯坦方程

将上述张量带入爱因斯坦方程(1)，由于是静态场，除了时间的流动之外没有其他维度的运动，因此(1)式只有00方向的分量。

(6)

这里我们需要注意到弱场条件，即时空虽不是非常平直但其变化比较平缓，这样的情况就符合弱场条件。弱场条件实际上满足很大一部分时空的实际情况，当然无法符合黑洞的时空结构。这种情况下，广义相对论可以看做是对牛顿时空的一级修正。这里有gAB=ηAB+hAB，其中|hAB|≪1

(7)

由(7)可以看到，由于是闵可夫斯基度规，是弱引力修正项。由于弱引力场的特殊情况，可以有：

ηAB=ηAB

(8)

hAB=hAB

(9)

(10)

(11)

(12)

(13)

考虑到闵可夫斯基度规是非连续的常量，求导为0，

η，A=η，B=η，D=0

(14)

所以(13)式演变为：

(15)

由于(15)式中的

-hCD(hDA，B+hDB，A- hAB，D)→0

(16)

这是由于h作为弱引力修正项已经足够小，其乘积可以忽略不计，所以(15)式变为：

(17)

三、静态引力场中爱因斯坦方程的解

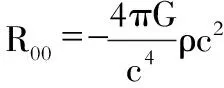
(6)

根据里契张量式：

(18)

因为(18)中右式的后两项是2阶无限小量，可以忽略，这样就有：

(19)

所以

(20)

根据

(17)

得到(取A=0，B=C，同时由于ηCD必须有C=D，否则为0)

(21)

(22)

在这里，如果C≠0，非时间维度，那么静引力场中其他维度不随时间变化，对其他维度求导为0，所以

hC0,C=0；h0C，C=0

(23)

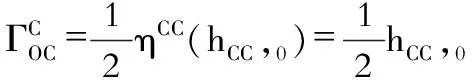
(24)

这是由于，ηCC=1，(当C≠1时)，ηCC=-1，当C=1时。但是，由于是静态引力场，所以hCC，0也为0，这是由于弱引力修正项同样不随时间变化，用时间对其求导结果依然是0。所以，终究有

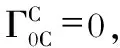
(25)

同样由于是静态弱引力场，弱引力修正项同样不随时间变化，如果用时间对其求导结果依然是0。同时，由于η的性质，必须有指标C=D，则

(26)

(27)

为了明显和方便起见，以常用的时间符号t代替指标C，得到：

(28)

再根据

(20)

得到：

(29)

四、静态引力场中爱因斯坦方程的解与万有引力定律的对比

由(29)式，再根据

(6)

就有

(30)

根据

(28)

得到：

(31)

整合一下数学表达式，就有：

(32)

其中，

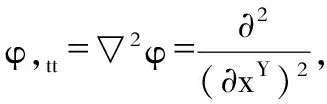
(33)

是我们熟知的若引力修正项，牛顿万有引力场的解是弱引力场下的唯一解。由此，我们可以确认：

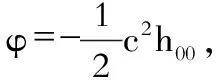
(34)

这样(32)式就化为牛顿引力场的泊松方程的形态：

(35)

以上事实说明，爱因斯坦方程在弱引力场条件下的解与牛顿的万有引力定律是一致的。广义相对论涵盖了万有引力定律。

五、万有引力定律的泊松表达式

(一)众所周知，牛顿万有引力定律的公式是

(36)

现在与广义相对论对接的是牛顿引力场的泊松方程的形态：

(35)

现在想说明的是(35)如何转化为(36)

首先，万有引力场的场强

(37)

如果引力源是一个连续体，体内任意一处的微质量元是

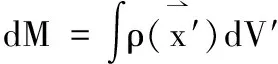
(38)

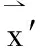
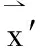
(39)

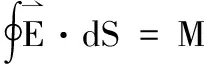
(40)

(41)

就是

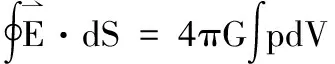
(43)

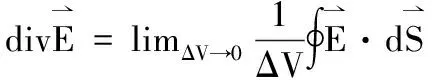
(44)

就会有：

(45)

(二)另外一方面：由于静态引力场是保守力场，就是说，引力对引力场中的物体做功的多少与物体的运动路径无关，只与物体的起始和终止的位置有关。所以单位质量的物体在静态引力场中由A点移动到B点，静态引力场对物体所做的功是：

(46)

此时引力势(单位质量的引力势能)必然下降，导致

(47)

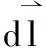
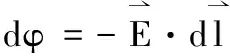
(48)

同时，

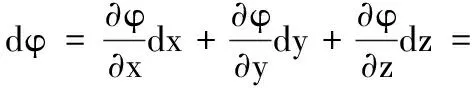
(49)

根据(48)和(49)，引力场强度等于引力势的负梯度，

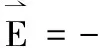
(50)

再根据

(45)

得到

(51)

其中：

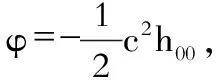
(34)

这就是万有引力定律的泊松表达方式。

上述事实说明，万有引力定律只是爱因斯坦引力场方程在静态、缓变的弱引力场中的近似表达方式。然而，广义相对论问世以后较长一段时间，由于天文学研究领域的局限性，广义相对论只被看成是牛顿引力定律在很小数量级上的修正。没有被足够重视。随着现代天文学的发展，这种情况才有了根本性的改变。

参考文献：

[1]唐肇华，刘素芸，翁甲强编著.广义相对论导论[M].桂林：广西师范大学出版社，1997.

[2]郭硕鸿编著.电动力学[M].北京：人民教育出版社，1980.

[3]费保俊编著.相对论与非欧几何[M].北京：科学出版社，2005.