用于四角固支的三角形瓦楞衬垫静态缓冲特性分析

王小芳，孙建明，李 昭，李华杰，孙旭东（河南科技大学，河南洛阳471023）

瓦楞纸板作为绿色环保的包装材料，在缓冲包装领域得到了普遍应用，它不仅具有良好的抗压性能和缓冲性能，而且价格低廉，方便回收再利用。为了更好地利用瓦楞纸板，让瓦楞纸板在缓冲包装领域发挥更加广泛的作用，有必要对传统瓦楞结构进行优化设计并研究其缓冲性能及规律，从而提高瓦楞缓冲包装的设计效率，提升瓦楞缓冲结构的保护性能[1-3]。

1 三角形支撑型四角固支瓦楞缓冲结构

基于现有瓦楞缓冲结构原型（如图1所示），提出了一种四角固支型局部瓦楞缓冲设计方案[4-7]。该结构特征如下：缓冲结构的四个角以特定的折叠形状对产品进行主要支撑，中间以瓦楞挡板对产品辅助固定，这种结构能够有效地支撑和固定产品，不仅避免了产品与外包装箱接触导致破坏，而且节省瓦楞材料、具有良好的缓冲性能，这种形式即四角固支瓦楞缓冲结构。三角形瓦楞衬垫成型结构简单，且稳定性好，故提出了三角形支撑型四角固支瓦楞缓冲结构，其每个支点均为楞向一致的三面承重形式（如图2所示）。本文对这种典型的结构形式进行简化，以主要的三角形支撑结构单元为研究对象，构建其缓冲结构试验模型，设计动态压缩试验，为后期合理设计三角形支撑型四角固支瓦楞缓冲结构尺寸提供依据。

2 静态缓冲试验模型

研究缓冲结构的动力学性能，衡量其对产品的保护能力，是通过试验测试来完成的。缓冲结构的性能测试分为静态压缩和动态压缩两种[8-9]。静态压缩性能测试是评价缓冲结构在产品堆码、存储等静止状态下承受静应力作用时的性能，通过沿厚度方向对试样逐渐增加载荷，并测试压载荷以及试样变形量，曲线拟合得到三角形瓦楞缓冲结构的压力—应变曲线[10]，再消除材料尺寸的影响，经过换算，得到其应力—应变曲线、缓冲系数—最大静应力曲线。

图1 四角固支瓦楞缓冲结构

图2 用于四角固支的三角形缓冲衬垫单元

本文所采用的三角形瓦楞缓冲结构的力学特性具有非线性特征（如图3所示）。缓冲厚度为t的瓦楞结构所受外力F与其压缩变形量x之间不是线性关系，且曲线与横坐标之间的面积对应缓冲结构的变形能[11-12]。

图3 瓦楞缓冲结构的非线性变形曲线

缓冲结构的变形能E可表示为：

式中，F表示试样所受压缩力；x表示试样压缩形变量。

单位厚度的瓦楞结构所吸收的变形能为E/t，此值与外力F之比表示缓冲结构的缓冲效率。即：

式中，E表示试样变形能；F表示试样所受压力；x表示试样形变量。

缓冲效率能够反映试样的缓冲性能，但在缓冲包装设计过程中，常用的参数是它的倒数，称为缓冲系数C。

在设计缓冲包装时，应选择缓冲系数较小的缓冲结构，以便节省用量。缓冲系数C与F、t、E三个参数有关，缓冲结构的缓冲系数，需要通过试验来测定。

3 静态压缩试验

3.1 瓦楞试样准备

瓦楞试样材料采用弹性较好、抗压强度高的UV齿形B型瓦楞纸板，具体配材及性能参数如表1所示。

表1 瓦楞纸板配材及性能参数

由于四角固支瓦楞缓冲结构的支撑处是瓦楞方向受力，因此试样在制作时，应保证楞向与承载方向一致。瓦楞纸板制作成等边三角形结构单元（如图4所示）。本次试样结构的边长a分为40mm、60mm、70mm、80mm、100mm五种规格，并将其的厚度t统一制作为50mm，同时每组试样的数量不少于3个。试验参照GB/T 4857.2-9包装温湿度调节处理中规定的方法，利用HC-302K型恒温恒湿箱进行处理，环境温度（25±2）℃，相对湿度（50±2）%。

图4 三角形瓦楞缓冲衬垫试样

3.2 试验原理及方法

静态压缩试验参考“GB 8168-2008包装用缓冲材料静态压缩试验方法”[13]进行，试验步骤采用方法B。试验前，首先对三角形瓦楞样品进行厚度测量，将测试厚度作为试验的原始厚度（T）。再用100N的载荷对样品进行预压5min，卸去载荷后，在三角形结构每条边上测量其三边的厚度，求出平均值，并精确到0.1mm。然后调整试验装置，在试样的正上方添加配重块，待百分表示数稳定后，记录变形量。

4 试验数据处理与曲线绘制

通过对所得的每组三角形瓦楞缓冲结构试样的数据测量、取样，得到试样的压缩力—形变量数据，再经过数据运算处理，可以得到应力—应变曲线，及缓冲系数—最大应力曲线。

4.1 试验数据

静态压缩试验过程中，对三角形瓦楞试样结构的加压速度极慢，近似于静载。在处理数据时，对同一载荷下的每组试样的变形量记录并求出平均值，作为该载荷下试样的变形量。以边长40mm的三角形缓冲结构试样为例，表2记录了其在不同载荷下的平均变形量。

表2 a=40mm三角形瓦楞试样在相应载荷下的平均变形量

4.2 压力—应变曲线[14]

压缩应力的计算见式（4）。其中，σ—静应力，单位为Pa；F—压缩载荷，单位为N；A—试样的承载面积，单位为mm2。

试样的压缩应变计算见式（5）。其中，ε—应变；Δt—试样的变形量，单位为mm；t—试样的初始厚度，单位为mm。

经过数据处理与计算，可得a=40mm三角形瓦楞缓冲结构的应力—应变曲线，如图5所示。

图5 a=40mm三角形缓冲结构应力—应变曲线

同理，可得到其他边长瓦楞缓冲结构的应力—应变曲线，如图6所示。

图6 不同边长a的三角形缓冲结构应力—应变曲线

4.3 缓冲系数—最大静应力曲线[15-16]

根据应力—应变曲线，经数值积分求得变形能后可算出相应的缓冲系数。表3为a=40mm三角形瓦楞缓冲结构静态缓冲系数按 ΔEn=（Δε×Δ）σ/2+Δε×σn-1差分格式数值积分的数据处理结果，并据此可绘制该三角形瓦楞结构的静态缓冲系数—最大静应力曲线（如图7所示）。

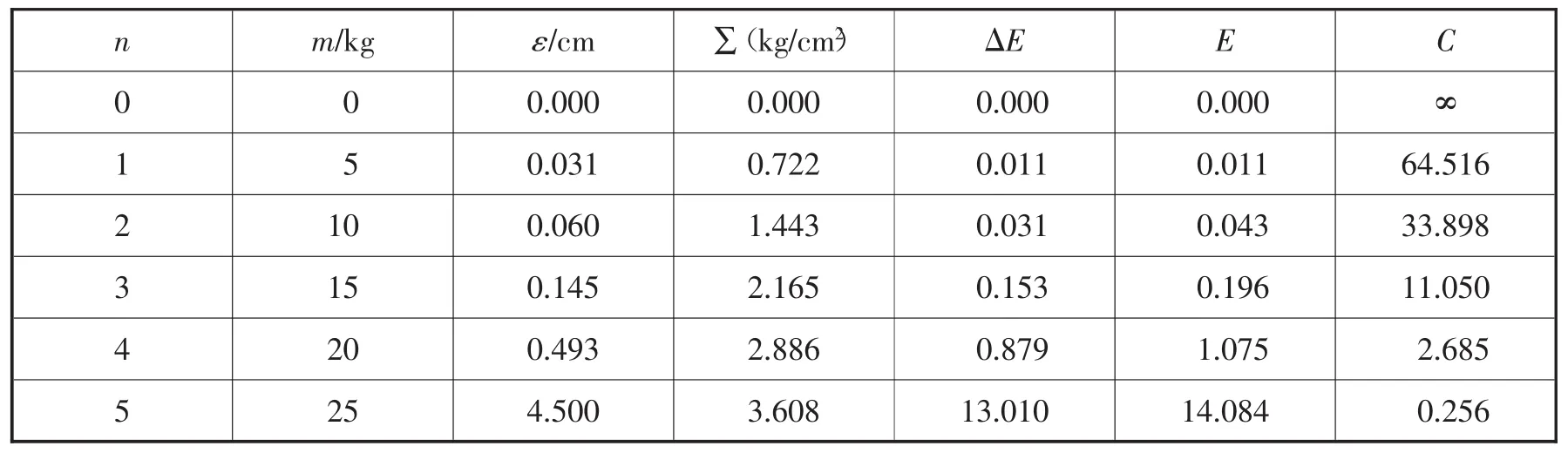
表3 a=40mm三角形瓦楞结构静态缓冲系数数据

图7 a=40mm三角形缓冲结构静态缓冲系数—最大静应力曲线

同理，可得到其他边长规格瓦楞缓冲结构的静态缓冲系数—最大静应力曲线，如图8所示。

5 静态缓冲特性分析

通过对不同边长三角形瓦楞缓冲衬垫试样进行静态压缩试验，发现该结构具有较好的抗压能力，能够承受较大的静态载荷。试验中，受制造工艺过程以及外界环境的影响，瓦楞纸板试样数据表现有一定差距，但不影响纸板性能的总体趋势。

（1）由于材料性质的原因，三角形瓦楞结构的静态压缩规律不同于EPS等塑料泡沫材料，该结构不存在最小缓冲系数。由静态缓冲系数—最大静应力曲线可知，该结构的缓冲系数随着静应力的增大而逐渐减小，最终趋于零。

（2）在一定载荷下，三角形瓦楞缓冲结构的形变是缓慢、连续的。当载荷较小时，试样的形变量较小，并能够快速稳定；但当载荷增加到一定程度时，试样变形量连续、缓慢的增加，至形变量稳定的时间较长。

（3）试样的压溃是由于受压边局部屈服而导致其内在结构发生破坏，失去继续承受更大载荷的能力。比较不同边长试样最终的压溃载荷可知，试样的边长越大，其最终的压溃载荷越大，表明其静态抗压性能越强。

（4）通过观察数据和对五组三角形瓦楞缓冲试样的应力—应变曲线研究发现，瓦楞试样为弹塑性结构。试样结构在压溃前分为两个不同的阶段：第一阶段类似于线弹性阶段，应变随着应力的增加大致呈线形增长的趋势；第二阶段呈现出塑性变形状态，曲线斜率逐渐平缓下来，这一状态下，应力增大到一定程度，试样被压溃，不存在曲服状态。表明当压缩载荷到达一定程度时，试样的抗压性能会大幅降低，失去支撑和缓冲能力。

（5）由曲线的走势及试验数据可知，当试样的应变小于5%时，应力和应变大致呈线性关系，结构的变形处于弹性阶段；随着载荷增加，应力增大，应力和应变呈现出明显的非线性关系；应变接近20%时，应力达到瓦楞结构的抗压强度极限，瓦楞结构被压溃。

6 结束语

本文提出了一种四角固支瓦楞缓冲包装结构，对其进行力学分析并简化模型，以四个角的三角形缓冲衬垫为研究对象。四角固支瓦楞缓冲设计属于局部缓冲结构，通过对关键四角的三角形基元结构构建静态试验模型，设计静态压缩试验方案，得到了不同压载荷下试样的变形量数据。在此基础上，曲线拟合得到该缓冲结构的应力—应变曲线，再消除材料尺寸的影响，得到其应力—应变曲线及缓冲系数—最大静应力曲线。试验表明，用于四角固支的三角形瓦楞缓冲结构衬垫具有较好的抗压能力，能够承受较大的静态载荷。更进一步，研究成果可用于四角固支瓦楞缓冲结构的开发和设计，为此类缓冲结构尺寸设计提供理论依据，促进瓦楞缓冲结构的发展、推广和应用。

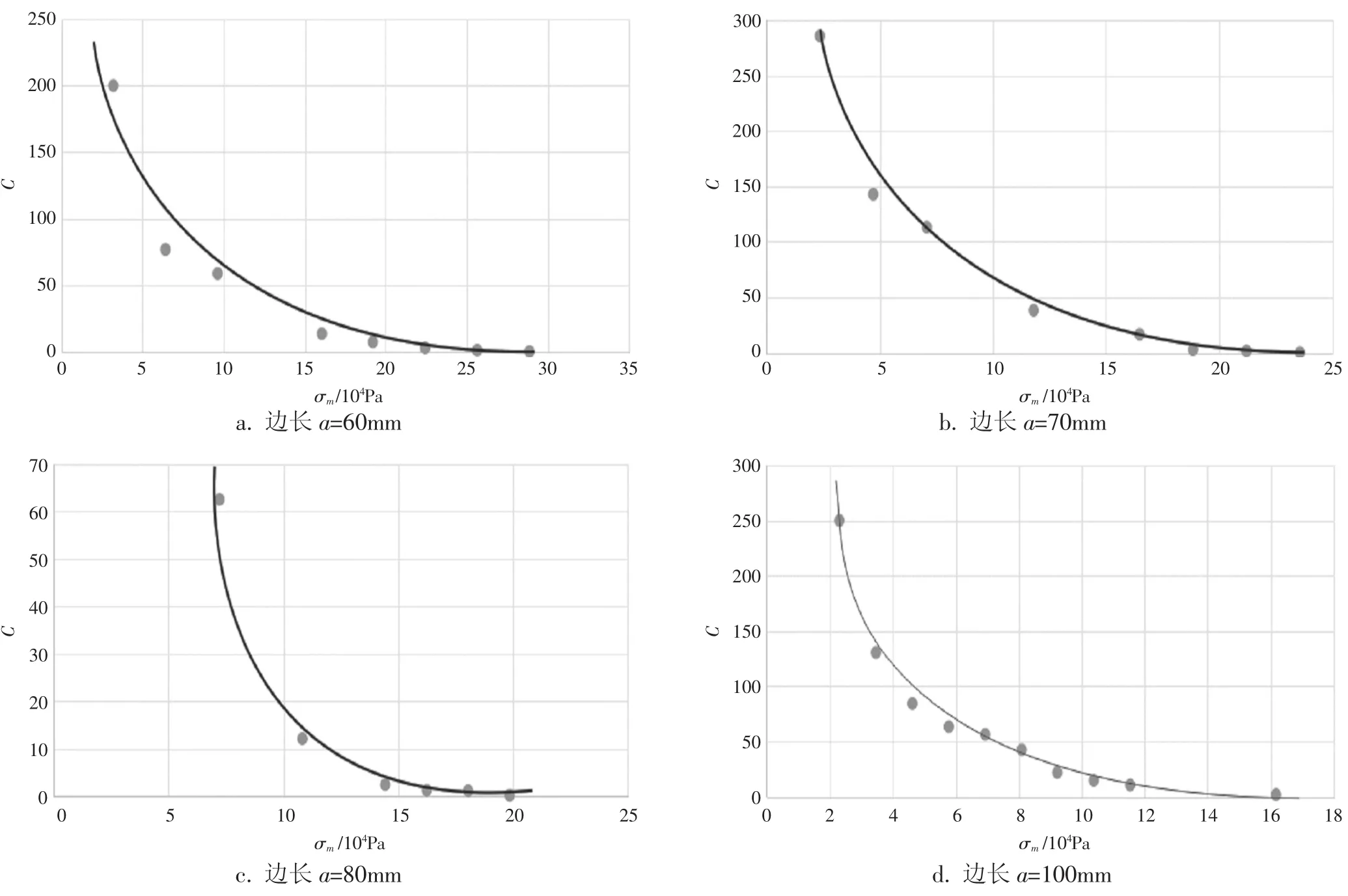
图8 不同边长a的三角形缓冲结构静态缓冲系数—最大静应力曲线

[1]刘艾，赵英芹，王玉龙,等.白酒包装件跌落有限元分析与优化设计[J].包装工程，2014(17):22-26.

[2]吴凯.绿色设计在包装领域的应用研究[D].曲阜：曲阜师范大学（硕士学位论文），2014.

[3]郑守斌，田大钢.快递包装中存在的问题及对策研究[J].物流科技，2015,38(1):123-124,132.

[4]TOMAS NORDSTRAND.Analysis and Testing of Corrugated Board Panels into the Post-buckling Regime[J].Composite Structures,2004(2):198-199.

[5]BLANCOLINI M.E,BRUTTI C.Numerical and Experimental Investigation of the Strength of Corrugated Board Packages[J].Packaging Technology and Science,2003(2):47-60.

[6]郭彦峰，许文才，付云岗,等.双瓦楞纸板衬垫结构的动态缓冲特性分析[J].包装工程，2008(4):7-9.

[7]郭彦峰，付云岗，马宴苹.折叠型双瓦楞纸板衬垫动态缓冲特性的试验研究[J].包装工程，2008(2):1-3.

[8]方婷.缓冲包装材料缓冲性能的研究[D].天津：天津科技大学（硕士学位论文），2013.

[9]孙聚杰.包装衬垫疲劳强度与疲劳缓冲性能的研究[D].无锡：江南大学（硕士学位论文），2007.

[10]都学飞，欧阳效卓，张汪年.EPS缓冲材料的静态压缩性能的试验研究[J].包装工程，2012(3):39-41,45.

[11]段艳健.瓦楞纸箱的屈曲和后屈曲研究[D].无锡：江南大学（硕士学位论文），2012.

[12]方艳平.瓦楞纸箱抗压试验研究与有限元分析[D].广州：暨南大学（硕士学位论文），2011.

[13]国家质量监督检验检疫总局，国家标准化管理委员会.GB/T 8168-2008包装用缓冲材料静态压缩试验方法[S].北京：中国标准出版社，2008.

[14]田金琛.瓦楞纸板缓冲结构件的缓冲性能研究[D].无锡：江南大学（硕士学位论文），2014.

[15]曾克俭，刘珊.蜂窝纸板动态缓冲性能分析研究[J].包装工程，2014(17):15-18.

[16]马宴苹.AB型双瓦楞纸板衬垫缓冲性能的试验研究[D].西安：西安理工大学（硕士学位论文），2007.