基于灰度关联分析法的卷积神经网络算法优化

刘梦雅，毛剑琳

(昆明理工大学 信息工程与自动化学院，云南 昆明 650500)

近年来，深度学习的发展使得机器学习取得了重要突破。其中，卷积神经网络 (CNN)在图像处理等方面的研究成果十分瞩目。它不但可以像人类视觉系统一样逐层提取得到图像的深层特征，提高网络的识别率；而且它提取到的特征具有较强的平移不变性，解决了由于图像变换引起的特征提取不准确的问题[1]。由于存在很多优点，目前卷积神经网络在虹膜识别、人脸识别、图像识别、语音识别等许多方面有着广泛的应用。

Lee等人[2]使用分层生成模型改进卷积神经网络来处理高维图像，大幅提高了准确率；Alex等[3]在处理图像识别问题时，构建了一种大型深层卷积神经网络，经测试发现，识别率得到了明显提高。目前提出的很多改进算法都取得了良好的识别效果，但对训练数据量的要求仍然较大，如果数据量较小就会导致卷积神经网络前几层得不到充分训练。为解决这一问题，权值的初始化操作是一个改进方向，文献[4]提出利用稀疏自动编码器学习输入图像的特征以初始化卷积神经网络的卷积核，之后文献[5]提出采用 PCA 改进初始权值的方法，但效果不佳，所以滤波器初值的优化仍然比较困难。

此外，卷积核的大小、池化模型以及特征图的个数都会影响CNN的运行速度和识别率。文献[6]比较了卷积核大小为19、15、11、7、3共5种情况下的实验结果，并得出结论：卷积核较小的情况更能拟合原始变化趋势，但是时间消耗巨大。文献[1]对不同池化模型进行了比较学习，并提出了一种改进的池化模型，使识别率得到了一定的提高。文献[7]比较了不同特征图个数下的识别率，发现当特征图的个数较少时，网络能够提取到的特征较少，使得识别率较低；但如果特征图的个数太多，识别率会有所提高，但会使网络的结构变复杂，训练时耗也会增大，还有可能出现过度训练现象。所以卷积神经网络隐层特征图数的确定至关重要。

本文提出了一种基于稀疏自动编码器和灰度关联分析法的卷积神经网络优化算法。首先，通过稀疏自动编码器产生一组滤波器集合作为卷积核的初始权值[8]，实验数据显示，卷积核初始权值的设定降低了初始均方误差。其次，引入灰度关联分析法筛选特征图，通过设定阈值确定隐层特征图个数，挑选出对输出层结点影响较大的特征图，删除部分对输出影响偏小的特征图。实验结果表明，在迭代次数较小的情况下，算法可以降低误识率，验证了算法的有效性。

1 卷积神经网络

卷积神经网络是一种深层神经网络，一般来说，它的基本结构包括5层，分别是输入层、卷积层、子采样层、全连接层和输出层。每层由多个二维平面构成，每个平面又由多个神经元构成。基本结构如图1所示。

原始输入图像首先经过卷积层，与卷积核进行卷积操作，得到一组卷积层特征图集合。这些特征被提取后，它们彼此间的位置关系不会再发生变化，所以卷积神经网络模型具有平移不变性。这些特征图再与子采样层的池化模型进行池化操作，对特征图进行二次特征提取。池化操作可以降低输入特征图的数据量，还可以避免出现过度训练现象。完成卷积和池化之后，把最后一层子采样特征图全部展开，重组成一个一维列向量(全连接层)，该一维列向量和输出层采用全连接的方式连接。

卷积神经网络通过输入特征图的感受域与卷积核进行卷积提取局部特征，和全连接方式相比，使得网络的参数大幅减少。计算时，多个卷积核分别对图像的不同感受域进行卷积，提取出多个特征图(每个卷积核卷积得到一幅与之对应的特征图)，此时，卷积核参数对所有的感受域而言都是不变的，所以大幅减少了训练参数，提升了网络的学习性能。但卷积神经网络在训练过程中仍有许多环节需要优化。在训练数据量不充足的情况下，CNN前几层网络的参数就不能得到较好的训练；但如果选用特别多训练数据又会导致网络训练速度缓慢，所以在适当数据量的情况下训练出较优的网络前层参数很重要。

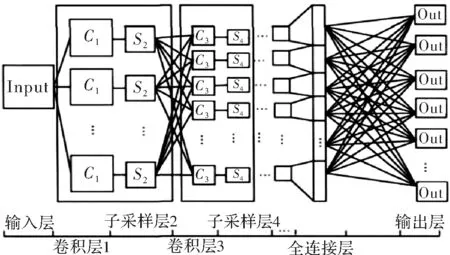
图1 卷积神经网络结构图

2 基于稀疏自动编码器进行无监督预训练

针对上述问题，本文采用稀疏自动编码器对初始特征图进行无监督预训练，得到一组能较好反映初始特征图特征的滤波器集合。将这组滤波器集合作为CNN的C1层卷积核，能有效降低网络的误识率。

稀疏自编码器(Sparse Autoencoder)可以自动从初始特征图中学习出它的特征，提炼出比原始数据更精炼的特征描述。用稀疏编码器提取的特征在实际运用中往往比原始数据更有助于网络的训练，其网络结构如图2所示。

图2 稀疏自动编码器结构图

稀疏自动编码器本质上是一个只具有一层隐含层的BP神经网络，其基本思想是使输出等于输入，使得编码器学习出输入特征图的另一种表达方式。BP神经网络在训练过程中，最终输出结果是与标签比对，并计算损失代价函数，而稀疏自动编码器没有预先设置好的标签，与网络输出对比的是输入本身。所以，稀疏自动编码器的训练过程与BP神经网络一致，也就是一种“信号正向传播，误差反向传播”的过程[9]，具体过程如下。

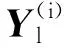
(1)

其中，f函数为激活函数，一般取tanh函数或者sigmoid函数，本文测试采用sigmoid函数。

稀疏自动编码器的目标函数为

y(i)=x(i)

(2)

可以通过最小化以下代价函数(3)，实现式(2)，即使输出值尽可能等于输入值

(3)

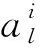
(4)

在原始的代价函数中加入一项额外的惩罚因子稀疏性限制条件以实现稀疏性，可以选择如式(5)形式的惩罚因子[10]，该表达式也被称为相对熵

(5)

ρ通常是一个较小的值，一般接近于0(如ρ=0.05)，表示神经元j的平均活跃度为0.05。此时的代价函数更新为

(6)

其中，β是稀疏性惩罚因子的权重。

上述部分是正向传播过程，接下来要对误差进行反向传播以实现权值的更新。采用的方法是和神经网络一致的BP反向传播算法[11]。权值更新公式如下

(7)

(8)

其中，α为学习率。不断迭代上述“信号正向传播，误差反向传播”的过程，实现权值的更新，直到算法收敛为止。最终得到的参数集Wl就是预训练的卷积核参数集。

3 基于灰度关联分析法优化CNN结构

卷积神经网络特征图的个数对网络的结构和识别效果均有很大的影响，很多情况下都是依靠开发者的经验选择[12]。本文采用灰度关联分析法对卷积神经网络的结构进行优化，以此确定卷积神经网络特征图的个数。

灰度关联分析法(Grey Relational Analysis, GRA)是著名学者邓聚龙首创的灰色系统理论中的经典方法[13]。GRA的基本思想是量化特征图的几何状态，再计算出参考序列和比较序列之间的关联度。关联度较大时，比较序列的几何发展情况与参考序列更为接近。GRA能够挖掘系统内部的关联度，计算量也比较小，能比较方便地应用到神经网络结构的优化中。

本文使用的CNN网络结构由两个卷积层和两个子采样层组成。卷积层经过池化操作得到子采样层的特征图，所以它们的个数相等。因此，只需要确定子采样层的特征图个数。在本次试验中，仅对S4层的特征图个数进行优化，下面是GRA优化卷积神经网络结构的步骤[14]。

假设输入层输入个数为N，对应的标签就是参考序列y,为(y1,y2,y3,…,yN)。假设S4层的特征图个数为n,每个特征图的输出即比较序列ti,为 (ti(1),ti(2),ti(3),…,ti(N)),i=1,2,3,…,n。一般情况下，GRA的第一步是对数据进行归一化处理，但由于卷积神经网络特征图的输出经过sigmoid函数处理后范围在0～1之间，所以可以直接求出比较序列与参考序列之间的关联系数，计算公式如式(9)所示。

(9)

其中，ρ为分辨率系数，在0～1之间，一般取0.5。

由于每个特征图均有多个特征系数，所以有必要将这些关联系数集中成一个值，即关联度，计算公式如(10)所示。

(10)

以上求出了n个特征图的输出与对应的标签之间的关联度，然后对关联度进行排序，设定关联度阈值。小于阀值的特征图可以考虑将其删除，仅保留关联性较大的特征图，以此得到最优的隐层特征图个数[15]。

4 卷积神经网络优化算法流程

本文提出的改进后的CNN算法流程图如图3所示。算法步骤如下：

(1)导入训练集与测试集，设定CNN的初始网络结构并对网络参数进行初始化；

(2)利用稀疏自动编码器预训练，得到CNN网络的第一个卷积层所对应的卷积核的初始参数；

(3)通过式(1)计算得到C1层的特征图；

(4)通过下采样层对C1层进行池化，得到S2层的特征图；

(5)与步骤(3)和(4)相似，得到C3层和S4层；

(6)将S4层所有的特征图展开成列向量，采用全连接的方式，经过分类器得到每个特征图对应的识别结果；

(7)提取S4层的特征图数据，并将每个特征层对应的识别结果作为灰度关联分析法的比较序列，对应的真实标签作为参考序列，计算各特征图与识别结果的关联度。选择关联度大于阈值的特征图，然后对CNN结构进行优化；

(8)在优化后的CNN网络结构下，重复步骤(1)～(6)，直到损失函数的值小于预设的阈值，或者达到最大迭代次数；

(9)利用测试集对训练过的网络进行测试，计算出误差率。

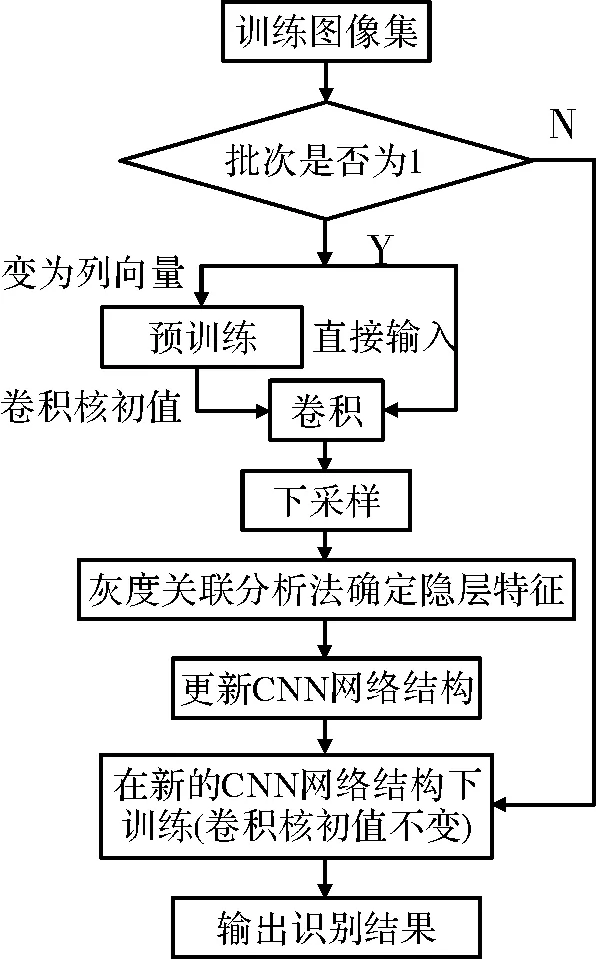
图3 优化后的CNN算法流程图

5 仿真实验及分析

本文利用全球手写数字MNIST数据集对改进后的CNN进行训练和测试。共有70 000条数据，选取60 000条数据进行网络的训练，其余数据进行测试。实验环境为Windows10，算法的实现平台为Matlab(2012a)。

试验中设置的CNN结构与参数如下：网络结构为两个卷积层和两个子采样层交替连接；C1层的隐藏特征图个数为6,C3层的隐藏特征图个数初始值为24，下采样层的特征图个数与对应的卷积层一致；卷积核尺寸为5×5，子采样层的池化模型为2×2；C1层卷积核初始化为稀疏自动编码器学习得到的滤波器集合，每层的偏置均初始化为0，其它权值初始值为设定范围内的任意值，在此不一一赘述。传统的CNN、预处理后的CNN以及基于GRA的改进CNN分别迭代一次后测试出的误识率如表1所示。

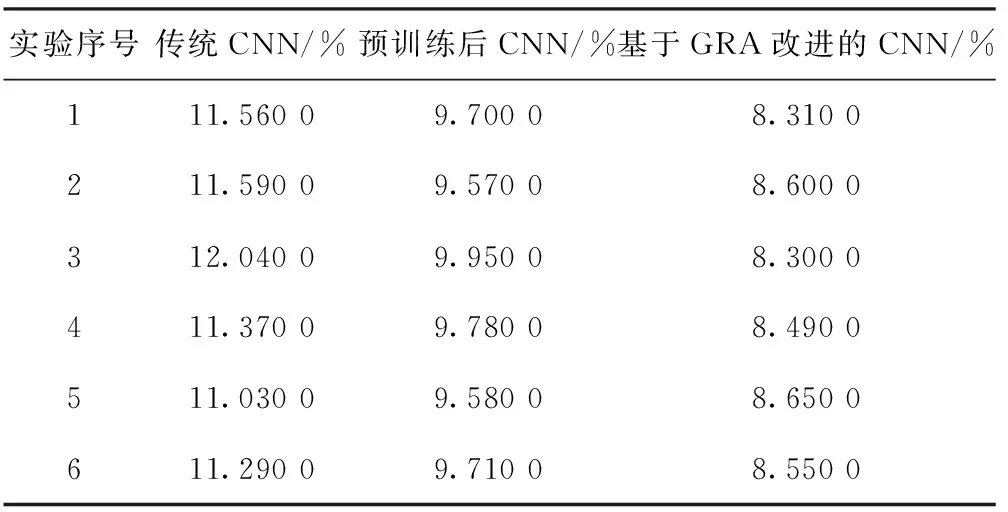
表1 3种算法迭代一次后的误识率

由表1可知，对传统的卷积神经网络进行无监督预训练后，误识率降低了约2%；再结合GRA对网络进行优化，误识率又降低了约1.2个百分点。所以，本文提出的改进算法在提高误识率方面确实有效果。

本次试验的C1层设置了6个隐藏特征图，所以在稀疏自动编码器进行预训练时，设置的中间层节点数为6。为使训练结果更形象得展示出来，试验对训练结果进行了可视化操作，稀疏自动编码器的训练结果如图4所示，GRA根据计算出的关联度选择特征图的过程如图5所示。

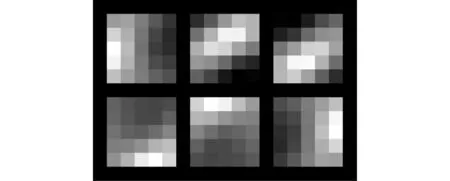
图4 稀疏自动编码器训练的滤波器集合

由图4和图5可知，稀疏自动编码器训练出了6个5×5大小的滤波器，提取出了能够较好反映原始输入图像特征的卷积核，GRA完成关联度排序后，会选择大于关联度阈值的特征图进行训练，这两步的引入为误识率的降低提供了可能性。

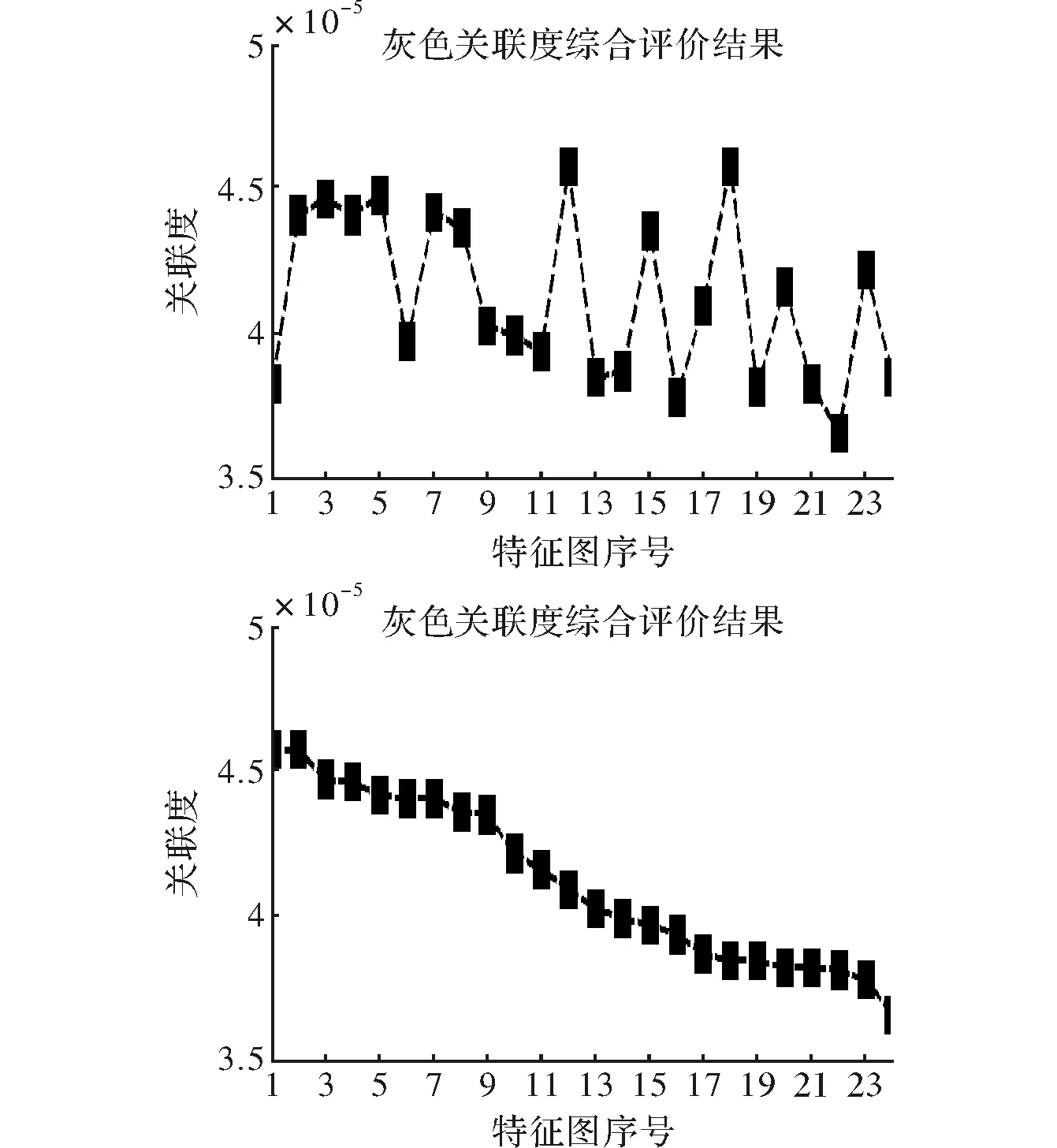
图5 灰度关联分析法对特征图进行关联度排序

除此之外，试验过程中Matlab绘出的均方误差图还说明随着预训练和GRA的引入，CNN的初始均方误差逐渐减小，由传统CNN的1.7到预训练CNN的1.3再到基于GRA改进CNN的1.18。均方误差的下降趋势也得到了改善，从图6可以直观的发现，改进后的算法均方误差下降迅速，收敛速度也有所提高。图6(a)描述的训练过程明显可见，在批次200～500之间出现了一个平台期，这段时间均方误差的下降趋势大幅减缓；图6(b)在批次200～400之间时均方误差的下降趋势也出现了减缓现象，但较图6(a)已经有了改进；图6(c)的训练过程中这一现象已基本消失。

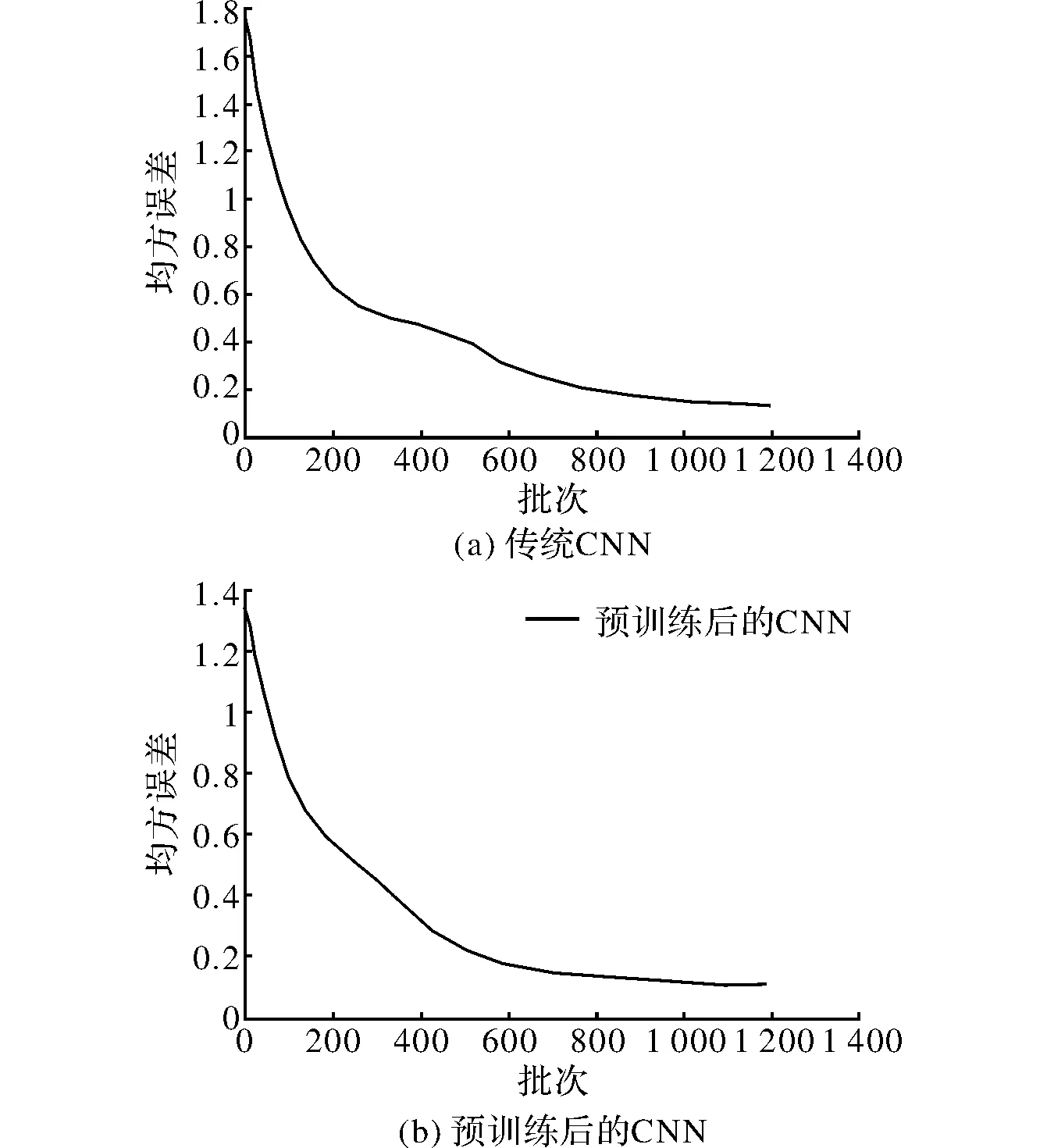
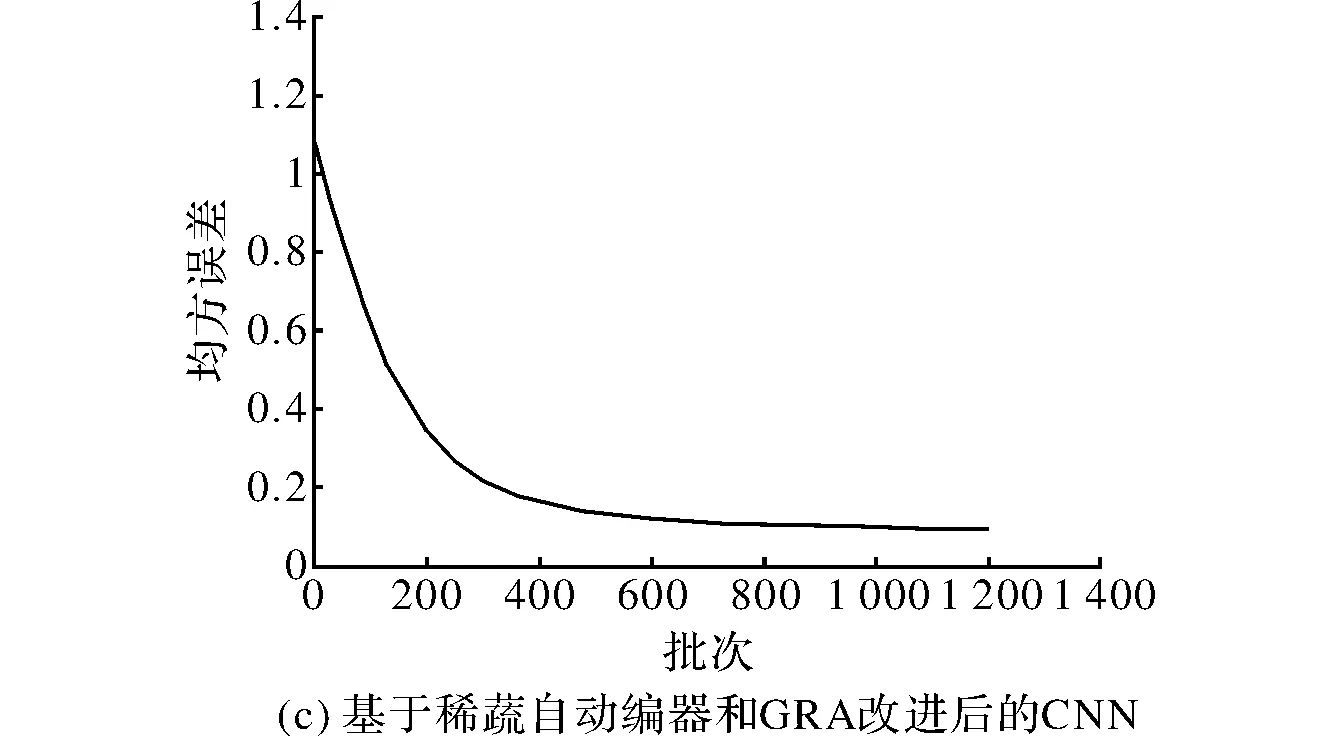
图6 3种CNN算法的均方误差

6 结束语

本文提出的改进的CNN算法，首先通过稀疏自动编码器对网络进行预训练，解决了卷积神经网络前层得不到充分训练的问题。然后，在对隐藏特征图的选择上，引入了灰度关联分析法，对卷积神经网络的结构进行了优化。试验结果表明，改进后的算法提高了传统CNN的识别率，对收敛速度也有一定的提高。但是，如果在数据量很大的情况下，改进后的算法就不再占优势，最终的识别结果差别不大。60 000条数据迭代10次时，3种CNN的识别结果均在98%左右。所以，本文提出的改进算法适用于数据量较小的情况，在这种情况下，可以较快地提高卷积神经网络的识别率。

[1] 刘万军,梁雪剑,曲海成.不同池化模型的卷积神经网络学习性能研究[J].中国图象图形学报,2016,21(9):1178-1190.

[2] Lee H,Grosse R,Ranganath R,et al.Convolutional deep belief networks for scalable unsupervised learning of hierarchical representations [C]. Montreal:Proceedings of the 26thAnnual International Conference on Machine Learning,ACM,2009.

[3] Alex K,Ilya S,Hinton G E.ImageNet classification with deep convolutional neural networks[EB/OL].(2015-02-10)[2017-05-13]http://papers.nips.cc/paper/4824-imagenet-Classification-withdeep-convolutional-neural-networks.pdf.

[4] Kavukcuoglu K,Sermanet P,Boureau Y,et al. Learning convolutional feature hierarchies for visual recognition[C].Vancouver:Proceedings of 2010 Advances in Neural Information Processing System Conference,Neural Information Processing System Foundation,2010.

[5] 史鹤欢,许悦雷,马时平,等.PCA预训练的卷积神经网络目标识别算法[J].西安电子科技大学学报:自然科学版,2016,43(3):175-180.

[6] 张贵勇.改进的卷积神经网络在金融预测中的应用研究[D].河南:郑州大学,2016.

[7] 李媛媛.卷积神经网络优化及其在图像识别中的应用[D].沈阳:沈阳工业大学,2016.

[8] 张文达,许悦雷,倪嘉成,等.基于多尺度分块卷积神经网络的图像目标识别算法[J].计算机应用,2016,36(4):1033-1038.

[9] 雒玉玺.稀疏自动编码器及其加速算法的研究[D].兰州:兰州大学,2014.

[10] 邓俊锋,张晓龙.基于自动编码器组合的深度学习优化方法[J].计算机应用,2016,36(3):697-702.

[11] 毕艳亮,宁芊,雷印杰,等.基于改进的遗传算法优化BP神经网络并用于红酒质量等级分类[J].计算机测量与控制,2016,24(1):226-228.

[12] Husken M.Structure optimization of neural networks for evolutionary design optimization[J]. Soft Computing-a Fusion of Foundations, Methodologies and Applications,2005,9(1):21-28.

[13] 唐万梅.BP神经网络网络结构优化问题的研究[J].系统工程理论与实践,2005(10):95-100.

[14] 杨延璞,陈登凯,顾蓉,等.基于色彩案例和灰度关联分析的产品配色设计方法[J].图学学报,2016,37(4):509-513.

[15] 王丽君,于莲芝.基于卷积神经网络的位置识别[J].电子科技,2017,30(1):104-106.