基于SVT变换的改进PCA多光谱图像融合

戎凯旋，韩新力，张学攀，芦存博

(1.中国电子科技集团公司第五十四研究所，河北 石家庄 050081;2.中国电子科技集团公司第二十二研究所，山东 青岛 266000；3.钱学森空间技术实验室，北京 100094)

由于传感器局限性，使得搭载有多光谱和全色传感器的光学卫星获得的卫星图像具有互补性[1]，即低空间分辨率的多光谱图像(Multispectral Image, MS)具有丰富的光谱信息，而高空间分辨率的全色图像(Panchromatic Image, PAN)光谱信息贫乏。实际应用中，高空间分辨率的多光谱图像更有助于进行图像理解与解译[2]，比如，在测绘领域，可以用于国土规划与探测；在军事领域，可以用于特征提取与特定目标检测等[3]。利用图像融合[4-5]手段，将多光谱和全色图像融合以获取高分辨率多光谱图像的技术即为多光谱图像融合(Multispectral Image Fusion)。这种技术关键是在提高多光谱图像空间分辨率的同时也要尽可能保持原有光谱信息不变，即不引起光谱失真(Spectral Distortion)[6]。

1 SVT变换

给定高斯径向基核函数(Gaussian Radial Basis Function, RBF)K(x,xj),j=1,2,…,N

(1)

其中，x是长度为N的向量，σ为扩展参数。根据式(2)计算出N×N的矩阵Ω

Ωij=k(X,XJ)+iij/γ,i=1,2,…,N

(2)

利用式(3)即可计算出N×N的矩阵Q

(3)

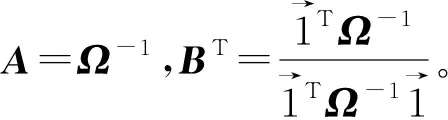
将支撑值滤波器在图像处理领域推广，针对不同空间分辨率的图像，通过在基本支撑滤波器中填充零的方式即可构造出一系列多尺度支撑值滤波器。相关文献已表明[9-10]，利用其对图像进行滤波，可以将图像中一系列的显著性特征提取出来。由于此类多尺度滤波器的非下采样性、各向异性以及移不变性的特点，给定一幅图像P，可以将P分解为高频细节信息Sj(j=1,2,…,r)和低频近似信息Pr+1相加的形式[8]：

(4)

其中，r表示分解层数，Sj=SVj*Pj，Pj+1=Pj-Sj,P1=P。其中SVj表示支撑值滤波器，*表示卷积。按照(4)式将细节信息与近似信息简单相加即可实现图像重构。

2 PCA融合

假设多光谱图像具有d个波段，每个波段图像大小为R×C，将每幅图像按照行优先一维化处理得到矢量化数据矩阵Y={ms'1, ms'2,…,ms'd}∈d×(R×C)。利用公式(5)计算其d×d的协方差矩阵covY

covY=(Y-E(Y))·(Y-E(Y))T

(5)

假设特征值λ1≥λ2,…,≥λd，对应的d×d变换矩阵为H={e1,e2,…,ed}，其中ei为λi对应的特征向量。按照公式(6)对Y实施变换

Y*=H(Y-E(Y))

(6)

经过上述变换后，Y*中第一主分量方差最大，包含了多光谱图像中大量的空间特征信息，而其他分量保留了多光谱图像的光谱信息。利用式(7)将全色图像与第一主分量做直方图匹配

(7)

3 基于SVT变换的改进PCA融合算法

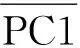
(8)

(9)

(10)

针对高低频分量，分别设计相应的融合规则进行融合。

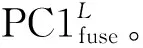
(11)

其中，σPANL和σPC1L分别表示PANL和PC1L的标准差。

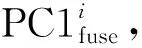
(12)

其中(m,n)表示像素位置，PC1fuse通过式(13)即可构造出来。

(13)

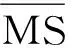
4 实验结果与分析

本文利用IKONOS(IK)和QuickBird(QB)卫星数据进行实验，并对实验结果进行讨论分析。其中IKONOS卫星多光谱和全色图像空间分辨率分别为4.0 m和1.0 m，QuickBird卫星多光谱和全色图像空间分辨率分别为2.0 m和0.5 m。图1给出了本文使用的四组图像数据，空间尺寸大小均为256×256。

图1 遥感源图像

利用传统PCA融合算法和基于SVT变换的融合算法[11]作为对比算法，其中SVT算法和本文算法的分解层数r设置为2[12]，SVT滤波器参数N，σ和γ分别设置为5，0.3和1[11]。利用相关系数(Correlation Coefficient，CC)[13]测量两幅图像的相关性，对于仿真数据实验，利用光谱角映射(Spectral Angle Mapper，SAM)[14]和整体相对合成误差(Erreur Relative Global Adimensionnelle de Synthese，ERGAS)[14]测量光谱失真，利用基于四元数理论的指标(Quaternion Theory-based Quality Index，Q4)[15]测量空间和光谱整体质量。对于真实数据实验，利用无需参考图的质量评价指标(Quality No Reference，QNR)[16]，Dλ和DS，其中Dλ测量光谱失真，DS测量空间失真，QNR综合测量空间和光谱的整体质量。CC，SAM，ERGAS，Q4，Dλ，DS和QNR的理想值分别为1，0，0，1，0，0和1。

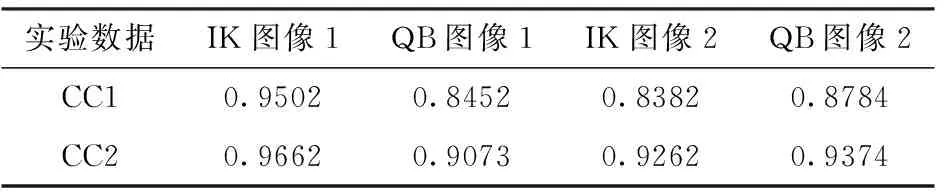
表1 相似性指标

图2 PC1fuse图像

图3给出了利用四组实验数据得到的融合结果，其中前两列为仿真数据结果，后两列为真实数据结果。对比图1可以看到，3种算法都提高了图1中多光谱图像的空间分辨率，与原多光谱图像相比，融合图像颜色没有发生明显变化，并且空间结构信息也与图1中全色图像一致。具体可以看到，图3前两列仿真数据结果的山棱、道路、建筑物，以及后两列真实数据结果的地形纹理和楼群边缘都很清晰。

图3 遥感图像结合结果

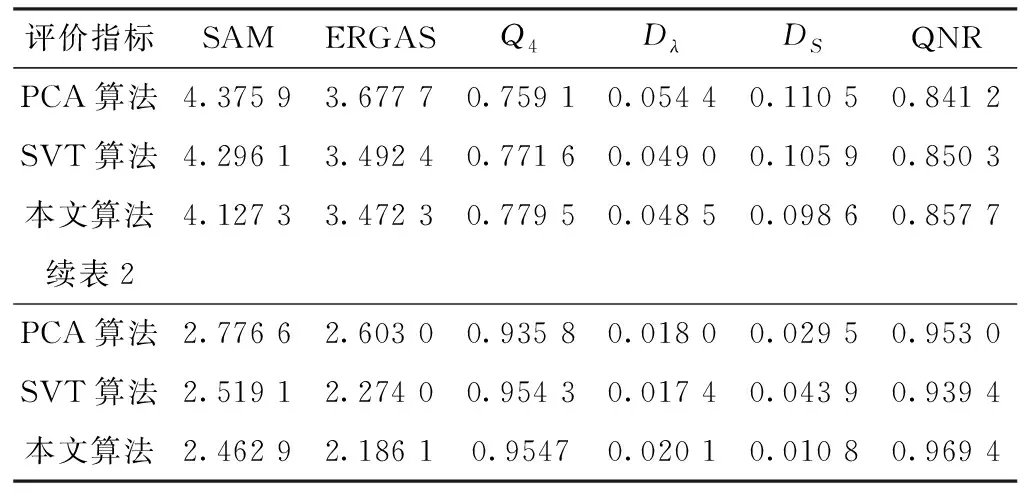
评价指标SAMERGASQ4DλDSQNRPCA算法4.375 93.677 70.759 10.054 40.110 50.841 2SVT算法4.296 13.492 40.771 60.049 00.105 90.850 3本文算法4.127 33.472 30.779 50.048 50.098 60.857 7续表2PCA算法2.776 62.603 00.935 80.018 00.029 50.953 0SVT算法2.519 12.274 00.954 30.017 40.043 90.939 4本文算法2.462 92.186 10.95470.020 10.010 80.969 4

5 结束语

针对传统PCA多光谱图像融合算法引起的光谱失真，本文利用SVT变换设计了一种融合策略来构造空间结构信息。实验分析表明，本文方法构造的PC1fuse更加相似于被替换的分量PAN，使得PC1fuse更适合于多光谱图像融合。与此同时，传统PCA融合算法的性能也得到了提升。本文下一步计划将图像的邻域相关性考虑进来，并设计基于此的高频信息融合规则，以进一步研究邻域相关性对算法性能的影响。

[1] 那彦,任梦乔.基于引导滤波的遥感图像融合算法[J].电子科技,2016,29(8):121-123.

[2] Xu Q,Zhang Y,Li B.Recent advances in pansharpening and key problems in applications[J]. International Journal of Image & Data Fusion,2014,5(3):175-195.

[3] 刘学,程大江,王峰,等.融合多重信息的图像局部不变特征描述[J].无线电通信技术, 2017,43(4):52-55,100.

[4] 那彦,焦李成.基于多分辨分析理论的图像融合方法[M].西安:西安电子科技大学出版社,2007.

[5] 李晓芬,金炜,安凯圣.基于小波变换和彩色变换的多聚焦图像融合[J].无线电通信技术,2015,41(2):85-88.

[6] Thomas C,Ranchin T,Wald L,et al.Synthesis of multispectral images to high spati al resolution: a critical review of fusion methods based on remote sensing physics[J].IEEE Transactions on Geoscience & Remote Sensing,2008,46(5):1301-1312.

[7] Jr P S C,Kwarteng A Y.Extracting spectral contrast in landsat thematic mapper im age data using selective principal component analysis[J].Photogrammetric Engineering & Remote Sensing,1989,55(3):339-348.

[8] Sheng Z,Shi W Z,Liu J,et al.Multisource image fusion method using support value transform[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society,2007,16(7):1831-9.

[9] Yang S,Wang M,Jiao L.Fusion of multispectral and panchromatic images based on support value transform and adaptive principal component analysis[J].Information Fusion,2012,13(3):177-184.

[10] 吴赟.压缩感知测量矩阵的研究[D].西安:西安电子科技大学,2012.

[11] Zheng S,Shi W Z,Liu J,et al.Remote sensing image fusion using multiscale mapped LS-SVM[J].IEEE Transactions on Geoscience & Remote Sensing,2008,46(5):1313-1322.

[12] Pradhan P S,King R L,Younan N H,et al.Estimation of the number of decomposition levels for a wavelet-based multiresolution multisensor image fusion[J].IEEE Transactions on Geoscience & Remote Sensing,2006,44(12):3674-3686.

[13] Karathanassi V,Kolokousis P,Ioannidou S.A comparison study on fusion methods using evaluation indicators[J]. International Journal of Remote Sensing,2007,28(10):2309-2341.

[14] Vivone G,Alparone L,Chanussot J,et al.A critical comparison among pansharpening algorithms[J].IEEE Transactions on Geoscience & Remote Sensing,2015,53(5):2565-2586.

[15] Alparone L,Baronti S,Garzelli A,et al.A global quality measurement of pan-sharpened multispectral imagery[J].IEEE Geoscience & Remote Sensing Letters,2004,1(4):313-317.

[16] Alparone L,Aiazzi B,Baronti S,et al.Multispectral and panchromatic data fusion assessment without reference[J].Photogrammetric Engineering & Remote Sensing, 2015,74(74):193-200.