基于振动测试的海洋平台结构简化模型

，，，

(1.东北石油大学，黑龙江 大庆 163318；2.大庆油田有限责任公司采油工程研究院，黑龙江 大庆 163712)

固定式海洋平台通过打桩的方法固定于海底，在长期服役过程中，由于受到腐蚀、疲劳、碰撞及恶劣的海洋环境等影响，平台结构会产生损伤，给海上石油生产带来风险。为了确保平台结构安全、降低维修成本及延长服役期限，国内外广泛开展了海洋平台结构损伤识别与健康监测技术研究工作[1-2]，以加强平台结构的完整性管理[3-4]。

目前，基于振动模态分析技术的结构损伤识别是一种通过结构的响应或动态特性的变化来对结构的整体性能进行损伤检测的方法。其核心思想是：结构一旦出现损伤，其物理参数(刚度、质量、阻尼等)将随之发生变化，相应地会导致结构的动态特性(模态参数)或响应的变化，根据这些指标的变化，就可以确定结构损伤发生的位置及程度。用于结构损伤识别的模态参数有固有频率、模态振型、模态振型曲率、柔度矩阵等。经理论研究表明[5]：结构的模态参数对刚度矩阵的影响与频率的平方成正比，而对柔度矩阵的影响与频率的平方成反比。所以只需低阶模态参数即能获得较高精度的柔度矩阵，弥补了在模态测试中结构高阶模态较难测得的缺陷。

在现役海洋平台结构的损伤识别与健康监测中，由于平台结构复杂、节点众多，水下部位振动传感器不易布置等因素，导致实测模态空间不完备问题突出[6]。因此，基于振动测试的海洋平台结构模型的简化就显得尤为重要。为此，根据低阶模态能较高精度地识别海洋平台结构柔度矩阵的特点，引入平台各层刚体运动的假设，利用海洋平台结构三维有限元模型，按柔度方法将平台简化为x、y向平动的串联多质点模型；通过平台水面以上传感器的布置，采用GUYAN振型扩展方法来估计未测量水下部位的振型值，解决实测模态信息不完备问题，为海洋平台结构损伤识别与健康监测提供便利。

1 简化模型

根据海洋平台结构的有限元模型计算结果，在建立简化模型时，仅考虑实际结构x与y方向的横向模态，不考虑各模态之间交叉的影响。在水平载荷的作用下，海洋平台各层的横截面作为刚体而产生运动，不发生变形，平台结构中立柱与斜杆完全处于弹性阶段[7]，见图1。

1.1 简化模型的质量

海洋平台结构简化模型按层进行结构离散，每层质点考虑x和y两个方向的平动质量，各层质点将层间质量的上半部分集中于上一质点，将层间质量的下半部分集中于下一质点。各质点的质量由有限元软件计算获得。

1.2 简化模型的刚度

按柔度方法简化模型基本步骤[8]：设海洋平台结构的分层数为i，每层的关键点数为j，在各层关键点的x和y方向分别依次施加1/j的单位力，从而可得到各节点x和y两个方向的线位移uij、vij，节点位移向量为

{fij}={uij,vij}

(1)

在简化模型中，该层对应的位移为

{fi}={ui,vi}

(2)

将位于平台同一层上各节点线位移值求和再平均，得到海洋平台结构多自由度简化模型(图2b)。模型中各层具有2个方向的线位移即柔度系数，集成各层的柔度系数得到海洋平台结构简化模型的柔度矩阵F，对其求逆，得到简化模型的刚度矩阵K，即

K=F-1

(3)

1.3 简化模型的动态特性分析

考虑无阻尼自由振动时，简化模型振动微分方程的特征值方程为

(K-λM)φ=0

(4)

式中：K为结构刚度矩阵；M为结构质量矩阵；φ为结构正则化振型；λ为结构固有频率的平方，即λ=ω2，rad/s，f=ω/(2π)，Hz。

求解特征值方程的特征值和特征向量，可得到海洋平台结构简化模型各阶频率和振型。

1.4 简化模型振型扩展

由于传感器只能在水面以上的结构上布置，水面以下海洋平台结构的振动情况即水下结构的模态振型无法知道。通过模态振型扩展方法，可使振动测试获得的试验模态自由度数扩展到数值模态的自由度数，实现基于振动测试识别海洋平台结构损伤之目的。

1.4.1 振型扩展方法

对于式(4)，按振动测点和扩展点进行分解得

式中：m为振动测点总数，s为扩展点总数。

根据式(5)可得到

φs=-(Kss-λMss)-1(Ksm-λMsm)φm

(6)

当忽略惯性作用时，式(6)变为

(7)

此式为Guyan静态扩展法[9]。

从式(7)可直接从已知测点的振型向量得到待扩展点的振型向量，然后按测点序号组集全节点振型矩阵。

1.4.2 模态置信准则MAC[10]

(8)

式(8)表示，MAC越大，说明2个振型的相关程度越好，反之越差。

2 数值计算与分析

对某海洋平台结构有限元模型和简化模型进行模态分析，并根据水面以上传感器测试结果，应用GUYAN方法，估算海洋平台水面以下结构的振型信息。

2.1 简化模型有限元分析

2.1.1 海洋平台结构基本参数

1)环境参数：水深80.0 m。

2)材料参数：弹性模量取200 GPa，泊松比取0.3，密度取7 800 kg/m3。

3)几何参数：平台总高100.0 m，水面以上结构高度18.0 m，泥面以下结构高度2.0 m。平台上甲板面积18.0×11.0 m2，海洋平台底部面积20.0×15.0 m2。甲板平面框架单元尺寸：截面积0.06 m2，高度0.3 m，宽度0.2 m。水平甲板单元厚度0.02 m。

上部甲板框架立柱的尺寸：直径0.5 m、壁厚0.02 m和直径0.3 m、壁厚0.015。海洋平台桩腿尺寸：0～82 m区域，直径1.2 m、壁厚0.03 m；82～100 m区域，直径0.8 m、壁厚0.02 m。

2.1.2 有限元模型与简化模型

某海洋平台结构简化模型见图2。

该平台结构有限元模型见图2a)，结构离散为409个节点，2 454个自由度。根据结构特点，按平台每层作为一个区域，共分为6个区域，每个区域x向有1个自由度、y向有1个自由度，这样原结构简化为各方向6个自由度多质点简化模型。其中简化模型的质点高度和质量见表1。

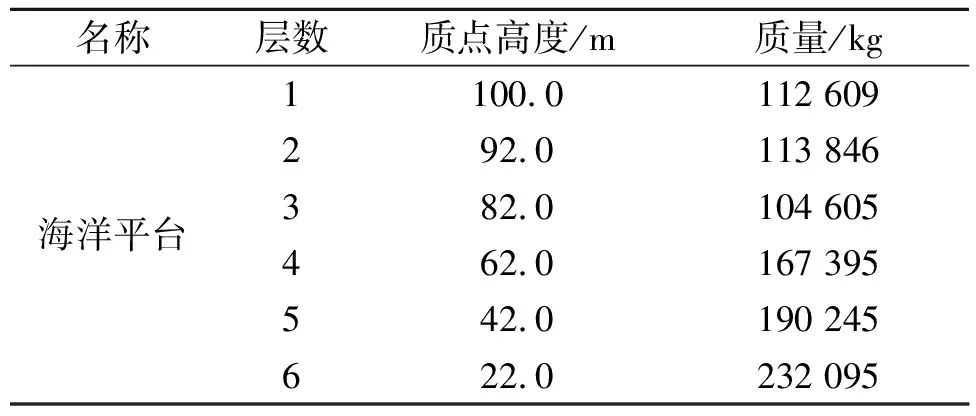
表1 海洋平台结构简化模型参数

2.1.3 有限元模型与简化模型模态参数

根据海洋平台结构三维有限元模型计算得到的简化模型质量(见表1)和柔度矩阵F，由式(3)可得到简化模型刚度矩阵K，根据式(4)求得简化模型的模态参数。结构有限元模型与简化模型在x和y向的固有频率fx和fy见表2。由表2可见，两者固有频率的误差最大为1.514 4%。

表2 有限元模型与简化模型固有频率(Hz)比较

2.2 简化模型振型扩展

由图2b)可见，传感器布置在水面以上一、二层平台的甲板上，此时平台x、y向的平动响应可以测得，即为主自由度。其余各层扩展点对应的自由度为从自由度，通过振型扩展方法，应用式(7)可得到其余4层从自由度(扩展点)的模态振型，并在振型中对质量进行了归一。图3为实测海洋平台结构x、y方向4阶振型的实测值与应用Guyan法的估算值对比图。

由图3a)、3b)表明，第1阶、第2阶模态未测试自由度的振型值得到了很好的估计，其与真实振型的MAC值为1，模态最大误差为0.696 6%。由图3c)、3d)估算的第3阶、第4阶振型MAC值与模态相对误差列于表3。

表3 Guyan方法前4阶振型与FEM前4阶振型的MAC值

由表3可见，利用Guyan方法在海洋平台结构低阶模态振型扩展上具有较高的精度，可满足工程应用要求。

3 结论

1)针对固定式海洋平台结构复杂、节点众多等特点，依据海洋平台各层刚体运动的假设，利用海洋平台三维有限元模型，按柔度方法将平台简化为x、y向平动的串联多质点模型。经实例计算，简化模型与有限元模型两者计算结果吻合较好，验证了简化模型的合理性。

2)在海洋平台振动测试中，通过平台水面以上传感器的布置，采用GUYAN振型扩展方法估计未测量水下部位的振型值，并通过MAC验证该方法的正确性。

上述方法对于海洋平台结构损伤识别与健康监测具有重要的意义。

[1] 刘杰鸣,李绂,黄维平,等.浅海导管架平台结构损伤诊断试验研究[J].海洋工程,2011,29(4):37-42

[2] FAN Wei, QIAO Pizhong. Vibration-based damage identification methods: a review and comparative study[J]. Structural Health Monitoring,2011,10(1)：83-111.

[3] API RP 2SIM. Structural Integrity Management of Fixed Offshore Structures[S]. American Petroleum Institute,2011.

[4] Narayanan Sambu Potty, Mohammad Kabir B. Mohd Akram. Structural integrity management for fixed offshore platforms in malaysia[J].International Journal of Civil,Structural,Construction and Architectural Engineering,2009,3(10)：18-26.

[5] PANDEY A K, BISWAS M. Damage detection in structures using changes in flexibility[J]. Journal of Sound and Vibration,1994,169(1)：3-17.

[6] HOSSEINLOU F, Mojtahedi A. Developing a robust simplified method for structural integrity monitoring of offshore jacket-type platform using recorded dynamic responses[J].Applied Ocean Research,2016,56:107-118.

[7] HASSAN H M, LOTFI A, DOLATSHAHI K M, et al. Inverse vibration technique for structural health monitoring of offshore jacketplatforms[J].2017,62:181-198.

[8] EI-REEDY M A. Offshore structures design, construction and maintenance[M]. Elsevier Pte Ltd.,2012.

[9] O’CALLAHAN J, AVITABILE P, RIEMER R. System equivalent reduction expansion process[C]. 7th International Modal Analysis Conference, LAS Vegas,January 1989:29-37.

[10] EWINS D J. Modal testing：Theory, practice and application [M]. 2nd ed. Baldock,Hertfordshire,England：Research Studies Press,2000.