液气-液喷射器尺寸设计方法
云发
(大连理工大学能源与动力学院 大连 116024)
喷射器主要由喷嘴、混合室、喉管、扩散室和吸入室组成,最根本的特性是工作、引射两股流体在质能转化的过程中不消耗机械功。Sun Dawen[1]提出喷射器的几何形状和尺寸必须随工况而变化,才能实现在不同运行工况下使喷射制冷循环取得最佳COP。
有关喷射器的初期研究多建立在实验的基础上,数值模拟模型以定常面积混合理论和等压混合理论为主。20世纪中叶至21世纪初期,液-液喷射器的研究有了较大进展,气-气喷射器由于在模拟模型中加入凝结与非等熵流动的影响也有了与实验数据契合度较高的理论成果,气-液喷射器的研究由于多相流的发展也取得了较多的理论成果。19世纪中叶,德国学者W. J. M. Rankine[2]最先提出了喷射器理论设计方法。在此理论基础上,S. B. Riffat等[3]提出了定压混合和定常面积混合两种理论,对部分结构简化后的喷射器进行了一维模型计算并对结果进行了实验验证。G. M. Carlomagno等[4-5]研究了喷射器出口壅塞对喷射器性能的影响,并提出结构优化的方法。Yan Jiwei等[6]实验研究了喷射器应用于R134a喷射制冷系统,并对COP随工质的变化进行了定性分析。陈亮等[7]研究了两相流喷射器内的射流发展过程,沿引射流体的流动方向分段对射流压力进行分析并得到喷射器的喷射系数和出口背压随冷凝温度与蒸发温度的变化特性。张金锐等[8]实验研究了新型CO2喷射器,结果证明:喷射系数为0.4~0.8、喷射器出口压力和喷射器引射端压力比为1.09~1.20时,喷射器的工作效率最高。夏在超等[9]结合CFD数值模拟与实验研究了喷射器结构对其性能的影响,结果证明在给定工作参数条件下,存在一个最佳喉嘴距使喷射系数达到最大,同时喷射器性能随扩散室的扩散角的增加而降低。张于峰等[10]在考虑了实际流体热力学性质、混合效率和激波等因素的基础上,建立了喷射器热力学模型,结果表明对于确定几何参数的喷射器,喷射系数主要取决于膨胀比与压缩比,二者分别随膨胀比的增加而增大,随压缩比的增加而减小。
此外,也有一些学者研究了两相喷射器及新型喷射制冷系统。王菲等[11]建立了两相喷射器热力学模型,以R141b为工质进行了相关性能的研究,结果表明:相比于等压混合模型,对混合室采用恒面积混合模型进行设计计算更合理。王征等[12]结合涡流管与喷射器提出一种新型制冷系统并进行了热力学分析,结果表明:新型制冷系统性能优于普通喷射制冷系统和闪蒸气旁通两级压缩制冷系统。李海军等[13]通过求解二维N-S方程模拟了蒸气喷射器内的流动混合过程,验证了喷射器内喷嘴出口后,膨胀波(压缩波)经混合层反复折射、转化、衰减的过程,以及在扩压室入口会产生斜激波的理论预测。戚大威等[14]使用了5种工况对喷射压缩蒸气制冷循环系统进行计算,结果表明此系统在低温工况下节能效果最优,制冷量最大可提高29%,压缩机功耗最大可降低65%,COP最大可提高63%。郭建等[15]提出使用等马赫数梯度法设计喷射器,依据该方法设计的喷射器同样包含喷嘴等关键组件,只是在设计形式上进行了优化和实用性上做出了一定的改良。
喷射器在发展过程中逐渐被划分为单相、两相两个主要研究领域。在实际工业应用中,工作流体为两相混合物的情况多有发生,国内外关于液气-液喷射器的研究文献较少。在工程应用中,喷射器的结构和尺寸设计不合理会直接影响喷射器的工作性能,不同于液-气喷射器与气-液喷射器,液气-液喷射器的工作流体是两相流体,这为喷射器的设计与内部流动研究增加了困难。但由于其具有结构简单、运行可靠、密封性能好,使混合、传能、传质及流体输送相结合等优点,在化工及环境保护等行业,有着广泛的应用价值。所以,有关液气-液喷射器尺寸设计方法的研究具有很大的应用价值。
1 设计方法
本文在喷射器内部流动过程及建立喷射制冷循环热力学模型过程中,为便于分析按照以下假设来简化模型:1)忽略制冷系统中的管路、冷凝器和蒸发器内的压力降及喷射器内的所有摩擦损失;2)用均相流模型描述制冷剂的状态,喷射器的工作制冷剂为气液均匀混合流体(忽略两相间的速度滑移),引射制冷剂为饱和相;3)忽略混合室内的制冷剂相变,即在引入修正系数的情况下假设该单制冷剂液气-液喷射器为液-液喷射器;4)流体在流动过程中经历的压缩与膨胀过程也是绝热的(壁面绝热)。
液-液喷射器尺寸设计方法已有较为成熟的发展,经过多年的实际应用日趋完善。液气-液喷射器与液-液喷射器的最大不同体现在工作流体的液气混合液中气相与液相介质之间的相对运动,以及气相介质由于压力变化而产生的膨胀与压缩,由于本设计假设混合室中不存在相变,即把流体处理为均相物质(比容等根据质量含气率与体积含气率代入修正),在传统液-液喷射器尺寸计算方法的基础上,于喷嘴段尺寸设计中引入修正系数δ的思路是可行的。
1.1 流动基本规律
1)气液两相喷射器内部流体的能量守恒方程:
ip+μih=(1+μ)ic
(1)
2)气液两相喷射器内部流体的质量守恒方程:
Mc=Mp+Mh=Mp+μMp=(1+μ)Mp
(2)
3)喷射器混合室中流体的动量守恒方程:
φ2(Mpwp+Mhwh)-Mcwc
=pcfc-ph(fc-fp1)-pp1fp1
(3)
4)随着气液两相之间传热传质过程的进行,混合室的末端发生了凝结激波,即流体流动需遵循激波方程[16]。
1.2 尺寸设计方法
在现有理论和实验研究的基础上,依据液-液、气-液喷射器的设计理论引入修正系数δ。由于液气-引液的过程中液态工作流体不易被压缩,而低含气率的液气混合物在均相流模型里可视为非弹性介质,所以计算方法倾向于液-引液过程,为表明内部确实存在微量相变,且考虑到本实验选用工质R22的物理特性,工作喷嘴的出口截面积由式(4)确定:
(4)
喷射器混合室的最佳截面积公式:
(5)
轴向尺寸,即喷嘴离混合室的距离lc和混合室的长度lm由式(6)确定:
当喷射系数μ≤0.5时,即当自由流束不超出始段时:
(6)
当喷射系数μ≥0.5时,即当自由流束不只包含始段,而且还包含基本段时:
(7)
其中,喷射系数μ可在工作流体、引射流体压力、温度及混合流体压力确定的情况下,根据已有经验公式计算得出。

图1 喷射式制冷系统循环Fig.1 Jet refrigeration system cycle
扩散室的双边扩张角的角度范围常取8°~10°,因此扩散室的长度lK可以根据角度确定:
lK=(6~7)(dc-d3)
(8)
扩散器的出口截面面积按下式确定:
(9)
本文的气液两相喷射器尺寸设计考虑到实验用铜管的直径,对扩散室出口直径进行了调整。为方便实验对比以确定最佳修正系数,在理论值的基础上选取临近的几组数据,分别在理论数值的基础上加上修正系数δ=0.85、0.95、1.00、1.05、1.15,得出5组喷射器尺寸如表1所示。由于喉嘴距过小会造成喷嘴出口自由流束过度膨胀撞击混合室壁面,所以在一定范围(<1.12倍)内适当增大喉嘴距。
2 实验研究
2.1 系统设计
为提出一种更为精确的液气-液喷射器尺寸设计方法,修正系数可以通过实验选取最优值,也可以通过计算机数值模拟实现。在已有液气-液喷射器相关实验中,工作流体由液气射流压缩器提供,引射流体由离心泵提供,通过闸阀调节工作压力、吸入压力和流量。液气射流压缩器提供工作流体具有结构简单等优点,同时存在工作流体含气率不可控等缺点。本文使用的喷射器尺寸是在定工况条件下设计的,考虑到可以通过设置压缩机入口制冷剂压力等工况,控制冷凝器工作工况,进而通过物性计算得知喷射器工作流体的含气率等必要参数,采用封闭循环系统的实验方式验证实验。

表1 对比实验的喷射器理论尺寸Tab.1 The ejector theoretical dimensions of comparison test
喷射式制冷系统循环如图1所示,主要由压缩机、冷凝器、喷射器、节流阀、蒸发器、气液分离器组成。喷射器的工作流体为针阀节流后的制冷剂液气混合物,满液式蒸发器内的制冷剂液体为引射流体,混合流体进入满液式蒸发器,蒸发器中的气体流入压缩机。工作流体通过引射液态制冷剂实现降温降压,引射流体被引射后进入蒸发器开始下一次局部循环。实验台如图2所示,主要实验部件为3 HP单冷空调,功率为1 900 W,电压为220 V,体积66 cm×68 cm×44 cm;采集卡为研华USB-4 711 A,16路模拟输入通道,12位分辨率,8路DI,8路DO,2路AO和1路32位计数器;实验采用金属管浮子流量计,测量范围为0~1 000 L/h和0~500 L/h(20 ℃水),压力损失7 kPa,电流20 mA;温度传感器供电电压9~36 V,精度等级±0.5 ℃。

图2 实验台Fig.2 Test bench
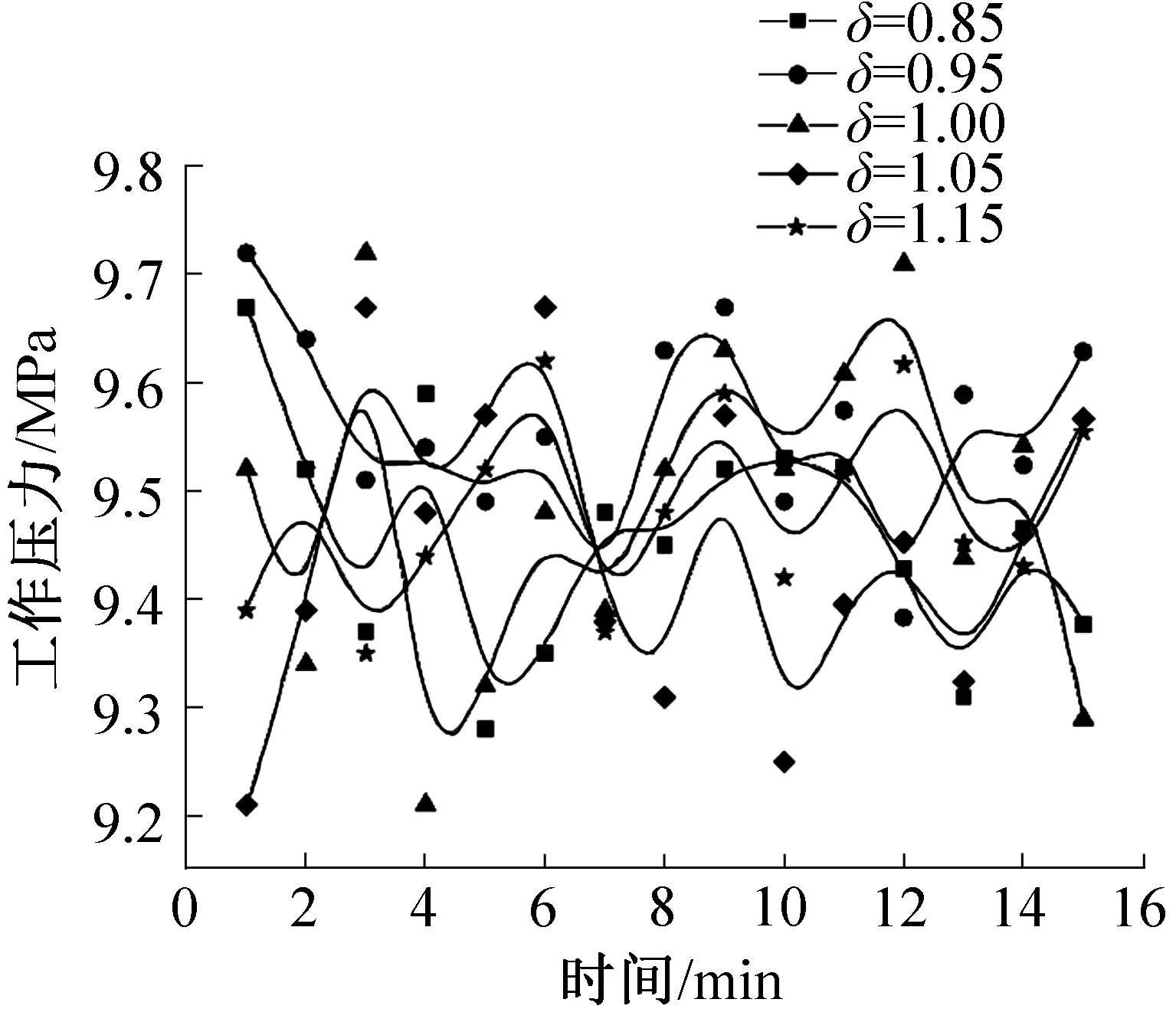
图3 制冷系统在5组喷射器下的工作压力Fig.3 The working pressures of the refrigeration system in the five ejectors
2.2 实验数据分析

图4 制冷系统在5组喷射器下的引射压力Fig.4 The discharge pressures of the refrigeration system in the five ejectors
本文设计工况为:工作压力0.95 MPa,引射压力0.45 MPa,混合压力0.5 MPa,喷射系数为0.3。系统运行稳定后,根据5组喷射器在相同时间节点下测得的工作压力、引射压力、混合压力绘制了B-spline曲线,分别如图3~图5所示。择优标准如下:1)曲线稳定性越高越好,与设计工况的偏差越小越好;2)喷射系数越大越好。曲线自身的稳定性通过方差大小来判断,在保证曲线自身稳定的基础上再比较均值与设计工况之间的偏差,这是因为把喷射器引入传统制冷循环的首要作用是保证系统仍能稳定工作,在此基础上再比较循环效率的提升,即喷射系数的大小。
由图3可知,5组数据的稳定性及与设计工况之间的标准差相差不大。但由图4与图5可以看出,不同喷射器尺寸下的制冷循环工况存在较大差异,需要借助标准差与均值进一步分析,如表2所示。

表2 实验数据自身稳定性分析及相对设计工况的偏差Tab.2 The stability analysis of the experimental data and the relative deviation of the design conditions
由表2可知,对比工作压力与设计工况,δ=0.95、1.15时的数据偏差最小且自身相对稳定;对比引射压力及混合压力与设计工况,δ=0.85、0.95时的稳定性和偏差明显优于其他组数据。通过喷射系数进一步比较二者的区别,图6所示为5组喷射器尺寸下的喷射系数。

图5 制冷系统在5组喷射器下的混合压力Fig.5 The mixing pressures of the refrigeration system in the five ejectors

图6 制冷系统在5组喷射器尺寸下的喷射系数Fig.6 The injection coefficient of the refrigeration system in the five ejectors
由图6可知,δ=0.85、0.95时喷射器的引射系数明显高于其他3组,且均与设计工况非常接近。由表3可知,δ=0.95时的喷射系数高于δ=0.85,故可认为δ=0.95时的喷射器尺寸最优。根据表3中5组喷射器尺寸下的喷射系数平均值,绘制如图7所示的折线图。由图7可知,喷射器的喷射系数在修正值δ=0.95时达到最高,然后逐渐下降。

图7 5组喷射器尺寸下的喷射系数平均值变化Fig.7 Variation curve of average injection coefficient in five groups of injectors
制冷管路的内摩擦不可避免的造成压头损失,虽然实验台整体采取了保温措施,但仍存在不可逆热损失,这些都是实验误差的重要来源。压缩机、蒸发器、冷凝器等未按照额定工况进行工作也可能是造成实验结果存在偏差的客观因素。需要指出的是,不同工况下,喷射器尺寸会随之变化,而本文修正系数的寻优主要通过实验方法实现,即不同工况下修正系数会有所不同。由于微型喷射器的加工难度限制,本文未对更多工况下修正系数的寻优进行实验研究,且修正系数的插入不仅消除喷嘴出口两相滑移对于流动的影响,也能弥补在计算方程推导过程中引入过多经验系数造成的误差,导致修正系数一定不会与系统工况呈函数关系变化,即不同工况下均需进行独立的修正系数最优值选取。

表3 5组喷射器尺寸下的喷射系数及其与设计工况的偏差Tab.3 The injection coefficient of five ejector sizes and the deviations from the design conditions
3 结论
使用喷射器与满液式蒸发器代替传统蒸气压缩制冷循环中的干式蒸发器,在新型喷射制冷系统运行工况为工作压力0.95 MPa,引射压力0.45 MPa,混合压力0.5 MPa时,对δ=0.85、0.95、1.00、1.05、1.15进行修正系数择优,结果表明:δ=0.95时,各测点工况符合设计工况,且实验所得喷射系数均值与经验公式计算值误差小于3%。采用喷射系数为验证因子来选取最佳喷嘴尺寸修正系数。以液-液、气-液喷射器的设计及理论推导为基础,在喷嘴段的计算中引入修正系数的尺寸设计方法具有充分的可行性。
符号说明
ip——工作流体的比焓,kJ/kg
ih——引射流体的比焓,kJ/kg
ic——混合流体的比焓,kJ/kg
μ——喷射系数
Mp——工作流体的质量流量,kg/s
Mh——引射流体的质量流量,kg/s
Mc——混合流体的质量流量,kg/s
φ2——混合室入口截面处的速度系数
wp——工作流体在缩放喷嘴出口截面的流速,m/s
wh——引射流体在混合室入口截面的流速,m/s
wc——混合流体在混合室出口截面的流速,m/s
pp1——工作流体在缩放喷嘴出口截面的静压力,Pa
pc——混合出口截面上混合流体的静压力,Pa
ph——引射流体的静压力,Pa
fc——混合室出口截面面积,m2
fp1——工作流体进入混合室时所占的截面积大小,m2
Gp——流量,kg/s
Δpp——喷嘴中的压力降,Pa
Δph——喷嘴中的压力降,Pa
Δpc——喷嘴中的压力降,Pa
vp——工作流体的比容,m3/kg
φ1——速度修正系数,本文取经验数值φ1=0.95
vh——引射介质的比容,m3/kg
vc——混合介质的比容,m3/kg
s——系统阻力,即喷射器所克服的阻力,kg/m7
lc——喷嘴离混合室的距离,mm
lm——混合室的长度,mm
lK——扩散室的长度,mm
a——实验常数,本文工况下取a=0.18
d1——工作喷嘴的出口直径,mm
d3——喷射器喉部直径,mm
dc——扩散器的出口截面直径,mm
δ——修正系数
ρc——混合室流体密度,kg/m3
下标
p——工作流体
h——引射流体
c——混合流体
m——代数,无实际意义
[1] SUN Dawen. Variable geometry ejectors and their applications in ejector refrigeration systems[J]. Energy, 1996, 21(10):919-929.
[2] RANKINE W J M. On the mathematical theory of combined streams[J]. Proceedings of the Royal Society of London, 1870, 19:90-94.
[3] RIFFAT S B, JIANG Liben, GAN Guohui. Recent development in ejector technology-a review[J]. International Journal of Ambient Energy, 2005, 26(1):13-26.
[4] CARLOMAGNO G M, IANIRO A. Thermo-fluid-dynamics of submerged jets impinging at short nozzle-to-plate distance: a review[J]. Experimental Thermal & Fluid Science, 2014, 58(10):15-35.
[5] ADDY A L, DUTTON J C, CMIKKELSEN C. Supersonic ejector-diffuser theory and experiments[J]. 1982.
[6] YAN Jiwei, CHEN Guangming, LIU Chengyan, et al. Experimental investigations on a R134a ejector applied in a refrigeration system[J]. Applied Thermal Engineering, 2017, 110:1061-1065.
[7] 陈亮, 刘敬辉, 陈江平, 等. 两相流喷射器流动模型研究[J]. 制冷学报, 2010, 31(2):26-31. (CHEN Liang, LIU Jinghui, CHEN Jiangping, et al. Study on flow model of two phase flow injection[J]. Journal of Refrigeration, 2010, 31 (2):26-31.)
[8] 张金锐, 吴静怡, EIKEVIK T M, 等. 二氧化碳喷射器运行效率的实验研究[J]. 制冷学报, 2016, 37(3):74-80. (ZHANG Jinrui, WU Jingyi, EIKEVIK T M, et al. Experimental investigation of R744 ejector efficiency[J]. Journal of Refrigeration, 2016, 37(3):74-80.)
[9] 夏在超, 李建新, 高德, 等. 几何结构对喷射器性能影响的CFD分析及实验研究[J]. 制冷学报, 2014, 35(3):45-49. (XIA Zaichao, LI Jianxin, GAO De, et al. CFD analysis and experimental study on the effect of geometries for the performance of an ejector[J]. Journal of Refrigeration, 2014, 35(3):45-49.)
[10] 张于峰, 赵薇, 田琦, 等. 喷射器性能及太阳能喷射制冷系统工质的优化[J]. 太阳能学报, 2007, 28(2):130-136. (ZHANG Yufeng, ZHAO Wei, TIAN Qi, et al. Investigation on performance of ejector and optimal refrigerants for solar ejector refrigeration system[J]. Acta Energiae Solaris Sinica, 2007, 28(2):130-136.)
[11] 王菲, 吕恒林, 冯伟, 等. 压缩/喷射制冷循环中两相喷射器性能[J]. 化工学报, 2012, 63(10):3094-3100. (WANG Fei, LYU Henglin, FENG Wei, et al. Performance of two-phase ejector in compression/ejection refrigeration cycle[J]. CIESC Journal, 2012, 63(10):3094-3100.)
[12] 王征, 李涛, 吴孔祥, 等. 一种利用喷射器和涡流管的新型制冷系统[J]. 工程热物理学报, 2012, 33(11):1843-1848. (WANG Zheng, LI Tao, WU Kongxiang, et al. The new refrigeration system with vortex tube and ejector[J]. Journal of Engineering Thermophysics, 2012, 33(11):1843-1848.)
[13] 李海军, 沈胜强. 蒸汽喷射制冷系统中喷射器内特殊流动现象的研究[J]. 工程热物理学报, 2006, 27(3):454-456. (LI Haijun, SHEN Shengqiang. Study on special phenomena in the ejector used in an steam ejector refrigeration system[J]. Journal of Engineering Thermophysics, 2006, 27(3):454-456.)
[14] 戚大威, 柳建华, 张良, 等. 蒸汽压缩/喷射制冷系统喷射器设计及节能分析[J]. 制冷学报, 2014, 35(1):103-108. (QI Dawei, LIU Jianhua, ZHANG Liang, et al. Ejector design and energy-saving analysis of vapor compression/ejection refrigeration system[J]. Journal of Refrigeration, 2014, 35(1):103-108.)
[15] 郭建, 沈恒根, 梁珍, 等. 喷射器结构改进方法及其CFD分析[J]. 低温与超导, 2009, 37(1):63-66. (GUO Jian, SHEN Henggen, LIANG Zhen, et al. Improvement on ejector design and CFD modelling[J]. Cryogenics and Superconductivity, 2009, 37(1):63-66.)
[16] SMOLLER J. Shock waves and reaction-diffusion equations[M]. Springer-Verlag, 1983.

