人工环境实验室送风风道结构的计算、验证及评价
(1 南京师范大学能源与机械工程学院 江苏省能源系统过程转化与减排技术工程实验室 南京 210042; 2 合肥通用机械研究院 合肥 230071)
随着国家节能减排政策的实施,空调制冷设备的能效要求也越来越高,因此对相关设备的性能测试愈发重要[1]。人工环境实验室作为检测各类空调制冷设备的测试装置,在采集被测试空调制冷设备样机(以下简称样机)性能数据时必须为样机提供均匀稳定的工况,样机周围的环境与标准工况越接近波动越小,得到测试结果的不确定度就越低[2]。国内外各类空调制冷设备的标准[3-5]详细说明了样机的实验工况条件及允许的变动幅值,以单元式空气调节机为例,GB/T 17758—2010中风冷型单元式空气调节机额定制冷的实验工况最大变动幅值为±1 ℃,平均变动幅值为±0.3 ℃。美国标准ANSI/ARI 210/240—2008中最大允许误差为2 ℉(1.1 ℃),平均允许误差为0.5 ℉(0.28 ℃)。人工环境实验室内部流场的均匀性越好,样机周围温度梯度波动越小,实验工况越稳定,因此研究人工环境实验室内部流场均匀性具有实际意义。
由于风道内部的静压作用[6-7],送风气流会通过实验室送风风道的各个出风口到达测试区域,因此人工环境实验室内部流场情况与送风风道各风口的出风量紧密相关,为均衡各风口的出风,国内外学者对其进行了研究。国外对变截面风道的研究主要集中在管内流体流动的计算模型与管道物性参数上,Li Tianyu等[8-9]对变截面管道进行了光滑曲管有限元处理,建立了任意形状的局部截面的运动学模型,通过沿弯曲管轴线挤压局部截面得到全局三维弯管,对4种弯管进行了数值模拟,并通过商业有限元程序包对模拟结果进行了验证,建立了变壁厚管结构管道单元计算模型。G. H. R. Kefayati等[10]优化了管内流体计算模型,探讨了屈服应力和水利直径对已有Bingham模型的影响并提出了相应的改进方式。滕琴等[11]介绍了变风口面积等截面与等风口面积变截面两种送风风道的均匀送风方式,并对设计计算进行了说明,举例展开了实际应用的计算方法和考虑因素,阐述了两者的适合场所与特点。李素玲等[12]在此基础上对变截面送风风道设计计算进行了详细的说明与推理,并优化了计算公式。肖婷等[13]利用计算流体力学的方法对变截面风管管内的气流组织进行了数值模拟研究,结果表明雷诺数越大,风管内的静压分布越均匀,送风均匀性越好;同时证实了变化风道截面面积对整个管内静压分布的平衡作用是均匀送风的主要原因。
但上述研究都是直接提出风道均匀送风的变截面方式,未对如何得到这种均匀变截面的方式进行充分的讨论说明,也未对这种方式与其他的改进方式进行对比分析;另一方面,目前的研究只是简单地将各风口的出风量进行对比,并未对送风风道提出一个合理的评价标准;上述研究只是对变截面送风风道进行了解析计算与模拟分析,并未对其实际结果进行测试验证。本文针对上述问题,以某人工环境实验室为基础,将原有的方形送风风道作为对照组,运用上述变截面送风原理对其分别进行了30°斜坡送风风道、45°斜坡送风风道、60°斜坡送风风道、等高度连续斜坡送风风道与等风量连续斜坡送风风道5种型式的结构设计,运用解析计算的方法得到上述6种送风风道在同一送风条件下各风口截面的出风速度,并通过实验对计算结果进行了验证,最后对送风风道提出了送风均匀性、送风效率与综合指标值3种评价指标,并得到了工程中人工环境实验室易于实现且具有有益效果的送风风道结构方式。
1 人工环境实验室结构
图1所示为某人工环境实验室室外侧结构,规格为7 400 mm(长)×6 200 mm(宽)×5 700 mm(高);送风口尺寸为1 110 mm×1 110 mm;回风口的尺寸为2 000 mm×800 mm;送风门的尺寸为700 mm×1 800 mm;送风百叶窗的尺寸为1 000 mm×1 600 mm;回风百叶窗的尺寸为1 500 mm×600 mm;两侧送风静压层的宽度为600 mm;上部回风静压层高度为700 mm。
实验室采用两侧送风上部回风的送回风方式,送风气流由室外空气处理机组从送风口送入静压腔体内,再由送风门送入送风静压层,通过送风百叶窗进入测试区域,经由回风百叶窗送到回风口。

图1 人工环境实验室室外侧结构Fig.1 Outdoor structure of the artificial environment laboratory
2 不同送风风道结构的设计与计算
流体在管内流动有沿程阻力与局部阻力[14-17],因此沿着空气流动方向,送风风道侧壁各风口的流速逐渐减小,对应的各风口出风量也逐渐减少,但由于送风风道在空间上的限制,而各个出风口的面积相等,可以通过变化风道的截面面积来实现各风口的近似均匀出风。在计算送风风道时,为了简化计算作如下假设:
1)用风口截面的平均流速和截面的平均静压代表该风口截面的流速和静压;
2)送风气流在送风风道中的流量系数及沿程阻力系数均为常数;
3)空气的流动仅由风道中的静压引起;
4)将第一个出风口截面的平均风速作为风道的平均送风风速。
图2所示为以图1的人工环境实验室送风风道为基础设计的带有等面积送风口的6种结构送风风道,风道除了送风口与各个出风口外其它位置是封闭的,各个结构的风道长度相等且各个送风口之间的距离相等,沿着风道长度方向的各送风口面积相等。
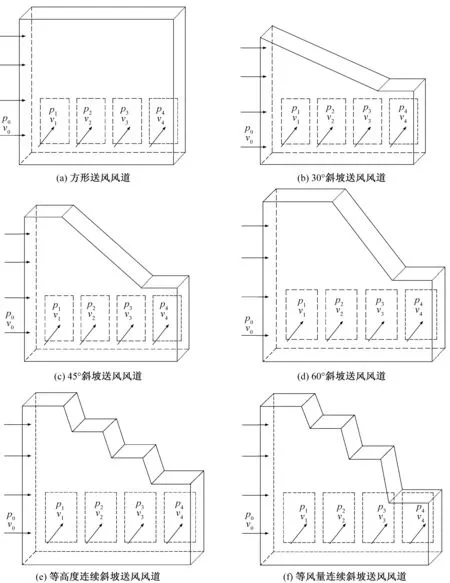
图2 6种典型送风风道结构Fig.2 Six structures of typical air supply duct
根据流体运动的能量方程[7],对于图2(a)~(e)所示的5种结构送风风道,推导出第i个和第i+1个风口中心截面的能量方程为:
(1)
式中:pi,pi+1分别为截面i和截面i+1的平均静压,Pa;vi,vi+1分别为截面i和截面i+1平均空气流速,m/s;ρ为空气密度,kg/m3;η为静压复得系数,一般取0.5~0.8;λ为沿程阻力系数,取决于流体雷诺数与风道粗糙度;li为i截面和i+1截面间的距离,m;Di为风道在i截面和i+1截面间的平均当量直径,将Di的值作为为Di和Di+1的平均值;a,b为局部阻力项和沿程阻力项的修正常数。
对于送风风道,若静压pi已知,则第i个送风口截面的送风速度为:
vi=μ(2pi/ρ)0.5
(2)
式中:μ为送风口流量系数。
根据式(2),若v1已知,便可以算出第一个送风口处的静压p1,再根据具体型式的风道尺寸依次迭代便可求出各个送风口的静压,从而得出各风口的送风速度。
对于图2(f)所示的等风量连续斜坡送风风道,已知各风口的出风量来计算出各个截面的高度,而对于结构(a)~(e)是已知结构求解各个风口的风量,故将式(1)的沿程阻力与局部阻力合成Δpi,则相邻两个出风口的能量方程可简化为:
(3)
式中:Δpi为风口i与风口i+1间的压降,即局部阻力与沿程阻力之和。
因各风口风量一致,而送风口面积一致各风口风速相等,再根据式(2)可得:
pi+1=pi
(4)
结合式(3)、式(4)得:
(5)
又因:
(6)
结合式(5)、式(6)可得:
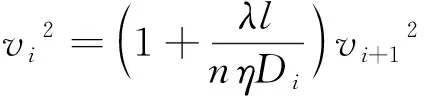
(7)
由于等风量连续斜坡送风风道的全部风量均由各个风口送出且每个风口的风量相等,则:
(8)
式中:Qi为风口i的风量,m3/s;Q0为入口风量,m3/s;n为风口数。
因此,等风量连续斜坡送风风道各出风口截面的水平隔板的高度为:
(9)
式中:bi为风口i处的风道高度,m;a为风道的宽度,m。
3 不同送风风道结构的计算结果与实验验证
3.1 不同送风风道的计算结果
图2中送风风道长度l=5.4 m,风道进口宽度a=0.6 m,高度b=5.0 m,送风口n=4,静压复得系数η=0.75,风道粗糙度Δ=0.15 mm,流量系数μ=0.65,取第一个出风口截面的平均风速为2 m/s,风道宽度a保持不变;对于3种倾斜导流板,图2(b)~(d)中右端水平板的长度为1.5 m,高度为2.6 m,倾斜板的角度分别为30°、45°和60°,其他条件相同;图2(e)中右端水平板的长度为1.5 m,高度为2.6 m,中间板的长度为1 m,中间隔板的竖直距离为0.84 m。
根据上述条件,该送风风道的入口处当量直径为1.07 m,因此该送风条件下空气的雷诺数为1.55×106>4 000为湍流,该雷诺数结合风道的粗糙度查莫迪图[18]可得式(1)与式(7)中沿程阻力系数λ=0.013,进一步结合式(1)和式(2)可得到5种结构下各风口的风速,结果如表1所示,表中a,b乘以20倍带入式(1)计算。
对于图2(f)的等风量连续斜坡送风风道,首先用式(7)计算出该风道各个风口截面的平均速度,再用式(8)计算出各风口的出风量,最后通过式(9)可得各风口截面隔板的高度,计算结果如表2所示。
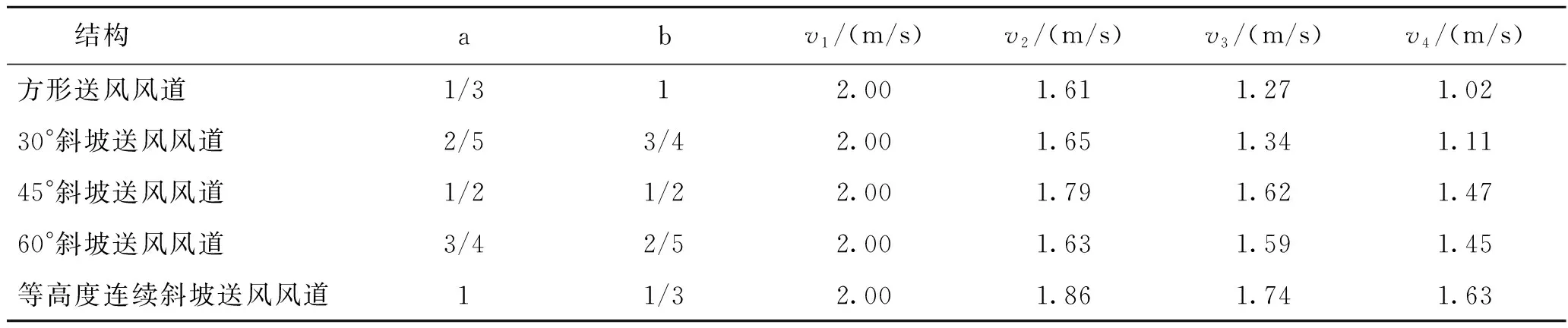
表1 不同风道结构的阻力修正常数与计算结果Tab.1 Drag coefficient and calculated results of different air duct structures

表2 等风量连续斜坡送风风道设计的计算结果Tab.2 Calculation results of continuous air supply duct with equal air volume
3.2 不同送风风道的实验验证
为了验证上文提出的近似计算方法结果的准确性,并为进一步推广该计算方法提供参考,需要测量图2中6种结构的各风口截面的实际风速。风速的测量采用Testo 416风速计,该仪器配备固定式16 mm直径叶轮探头,连接伸缩手柄,最长890 mm。该风速仪的量程为1~40 m/s;风速测量的不确定度Δ仪为±(0.2±1.5%×测量值)m/s,即文中3.3节中的系统不确定度ΔA。
由于本文的计算结果为各风口截面的平均速度[19-21],因此需要对截面的多个测点进行测试并计算平均速度,风道风口截面的宽度为定值600 mm,将其分成2段,各个结构的截面高度是不断变化的,取截面高度的1/5为一段进行划分,60°斜坡送风风道侧视图如图3所示,具体的测点布置如图4所示。每种结构的送风风道都有10个区域,取每个区域的中心作为该区域的测试值,每个测点测量3次,每次间隔10 s,取3次测试平均值作为该区域的测量值,最后将10个区域的平均值作为该截面速度的最终测量值,最终测试结果如图5所示。
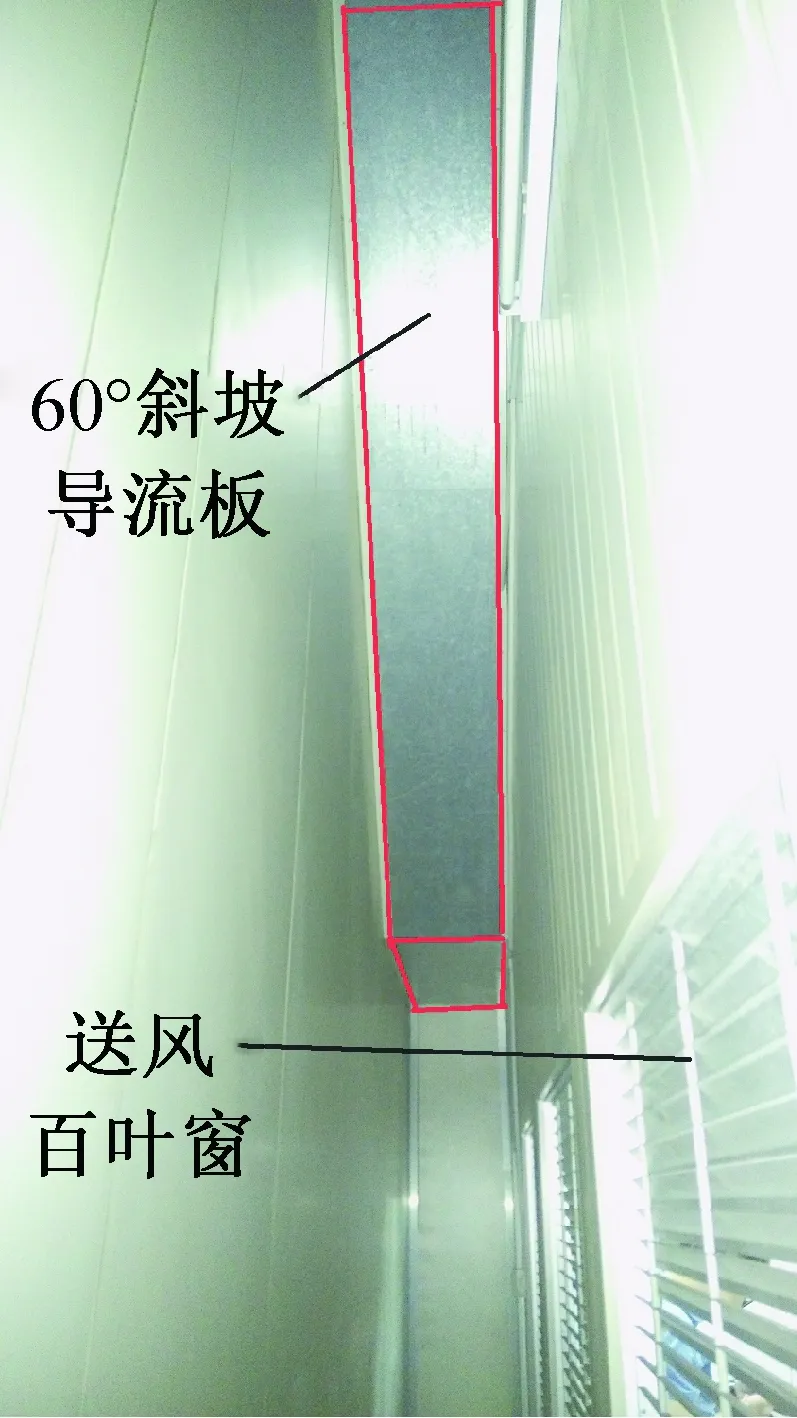
图3 60°斜坡送风风道侧视图Fig.3 Side view of 60° slope air supply duct

图4 60°斜坡送风风道内部测点布置Fig.4 Layout of measuring points in 60° slope air supply duct
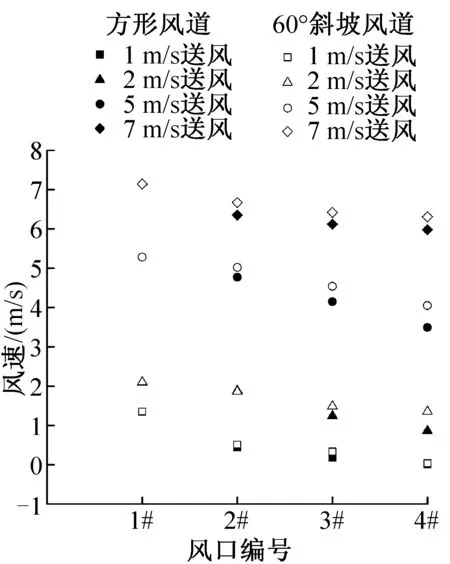
图5 方形风道与60°斜坡风道不同送风速度实测Fig.5 Actual velocity measurement of square duct and 60°slope air supply duct
当送风平均风速过小时[22-23],风道内部静压很小,造成离送风处远的出风口衰减至无风速的现象;当送风平均风速过大时,风道内部静压过大,造成相邻出风口截面平均风速相差很小,虽然能保证送风风道内部风速的均匀性,但会造成最后一个出风口的返流速度过大。上述两种状况下,变化风道的结构便会无意义,因此需要对送风风速有一定要求。本实验通过改变入口风速测量方形送风风道与60°斜坡送风风道各风口截面平均风速的大小以选择该风道结构下合理的送风速度范围,结果表明送风平均风速为2~6 m/s时变化送风风道结构对各风口截面风速分布效果显著。
3.3 理论计算与实验结果对比
对比3.1中计算得到的6种结构送风风道各风口速度的结果与3.2实测得到的结果,如图6所示。

图6 6种结构送风风道各风口截面风速计算与实测结果对比Fig.6 Comparison of calculated cross section wind velocity and measured results of six types of air supply duct
通过图6可以计算得出实测值与计算值的最大相对误差为16.35%,误差在可接受范围内,说明该种对于送风风道近似计算的方法具有一定的推广价值,故本文第4节的指标评价采用3.1节中的计算结果进行分析。图6中计算值的各风口风速下降有一定的梯度性,但实测值中1#风口与2#风口之间、3#风口与4#风口之间的风速下降趋势较计算值小,而2#风口与3#风口的风速下降趋势较计算值更为显著。
依据我国测量的行业标准JJF1059—2012[24],测量不确定度的定义是:与测量结果相关联的一个参数,用以合理地表征测量结果的分散性。不确定度值指测量结果偏离实际情况的程度,用分散性尺度来评价测量结果质量,综合了全部误差因素对实验结果的影响。不确定度分析理论[25-26]是误差理论的进一步发展,主要按不确定度来源分为系统不确定度和随机不确定度,系统不确定度可以根据经验、资料或仪器说明书评定,而随机不确定度可以根据直接测量样本标准差来获得,计算方法如式(10),计算结果如表3所示,最大不确定度为0.182,表明本文实验得到的测量值离散程度在可接受范围内,准确度较高。
(10)
式中:ΔX为合成不确定度,即最终所求不确定度值;ΔA为系统不确定度,取ΔA=Δ仪;ΔB为随机不确定度。

表3 6种送风风道结构的实测结果的不确定度Tab.3 Uncertainty of measured results of six typesof air supply duct
4 送风风道的指标评价
4.1 均匀性指标
送风风道的不均匀性[27-28]具体表现在各出风口的风速与平均送风风速的差异上,本文以不均匀系数作为不同结构送风风道的均匀性指标,其值越小表明该结构送风风道的均匀性越好,第i个出风口的送风不均匀系数σi用式(11)计算,进一步可以用各风口不均匀系数的平均值来代表该种结构风道结构的不均匀系数,计算结果如表4所示。
(11)


表4 均匀性评价指标下6种结构送风风道的不均匀系数Tab.4 Uniformity coefficients of six types of air supply duct under the uniformity evaluation index
4.2 送风效率(压降)指标
风道的送风效率[29-31]具体表现在各出风口的静压与平均送风静压的差异上,本文以送风压降系数作为不同结构送风风道的送风效率指标,其值越大表明该结构下送风风道的送风效率越高,第i个出风口的送风压降系数ηi用式(12)计算,进一步可以用各风口压降系数的平均值来代表该种结构风道结构的压降系数,计算结果如表5。
(12)

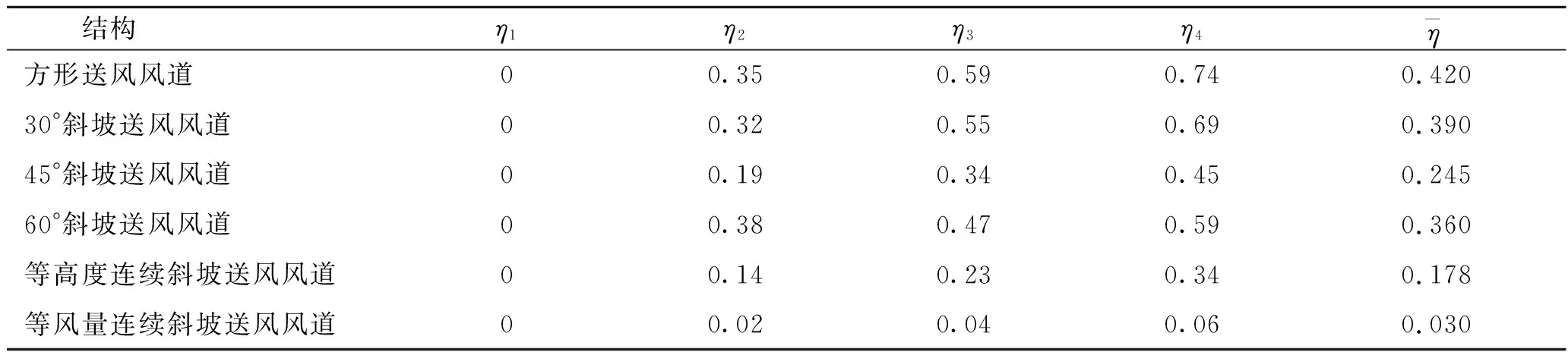
表5 送风效率评价指标下6种结构送风风道的压降系数Tab.5 Pressure drop coefficient of six air supply duct under the evaluation index of air supply efficiency
表5为6种结构送风风道的压降系数,其值越小,说明送风风道各出风口之间的压力变化越小,排出相等风量所需时间越长。结果表明,方形送风风道的送风效率最佳,压降系数为0.420;均匀送风风道的送风效率最差,压降系数仅为0.030。
4.3 综合指标
送风风道的综合指标即在考虑各风口均匀送风的前提下,考虑送风效率,即压降系数,由于两者对风道的有效效果相背,将各种结构的压降系数平均值与不均匀系数平均值的比值作为该种结构的综合指标ζ,如式(13),计算结果见表6。
(13)

表6为6种结构送风风道的综合评价指标,其值越大,说明送风风道在送风均匀性与送风效率上综合效果越优。结果表明,60°斜坡送风风道的综合指标最佳,ζ=2.28;均匀性最佳的等风量连续斜坡送风风道的综合指标略低,ζ=2.00。

表6 6种结构送风风道的综合指标ζTab.6 Comprehensive index value of six types ofair supply duct
5 结论
本文以某人工环境实验室为基础,将原有的方形送风风道作为对照组,进行了30°/45°/60°斜坡送风风道、等高度/等风量连续斜坡送风风道5种型式的结构设计,对这6种结构进行同一送风速度下各风口截面出风速度的理论计算,并通过实验对计算结果进行了验证,最后对送风风道提出了送风均匀性、送风效率与综合指标3种评价指标,主要结论如下:
1)该人工环境实验室原有方形送风风道的不均匀系数为0.265,压降系数为0.420,综合指标为1.58;等高度连续斜坡送风风道的不均匀系数为0.098,压降系数为0.178,综合指标为1.82;等风量连续斜坡送风风道的不均匀系数仅为0.015,压降系数为0.030,综合指标为2.00。
2)对于3种角度的斜坡式送风风道,30°斜坡送风风道的不均匀系数为0.235,压降系数为0.390;综合指标为1.66;45°斜坡送风风道的不均匀系数为0.145,压降系数为0.245,综合指标为1.69;60°斜坡送风风道的不均匀系数为0.158,压降系数为0.360,综合指标为2.28。
3)若以均匀性作为送风风道的评价指标,则等风量连续斜坡送风风道的效果最佳,仅考虑风道送风均匀性时选取该结构设计;若以送风效率作为送风风道的指标,则方形送风风道的压降最大,仅考虑风道送风效率时选取该结构设计;若从综合指标值出发,60°斜坡送风风道的综合效果最佳,该结构设计不仅综合考虑了送风均匀性与效率且较等风量连续斜坡送风风道的制作工程量大大减少,工程上人工环境实验室推荐使用该结构设计,且可推荐的送风速度范围为2~6 m/s。
4)对于本文提出的送风均匀性指标、送风效率指标与综合指标3种评价方式,综合评价指标同时兼顾了送风风道的均匀性与送风效率,送风风道在采用该指标时在达到一定送风均匀性要求的前提下会有相应的送风效率要求,减少了空气处理设备的运行时间,起到减少能耗的作用。
本文受江苏省教育厅高校自然科学基金(15KJD470001)资助项目。(The project was supported by the Higher Education Institutions of Jiangsu Province (No.15KJD470001).)
[1] 李晓凤, 马一太, 闫秋辉. 房间空调器的热力完善度分析[J]. 制冷学报, 2013, 35(1):18-23. (LI Xiaofeng, MA Yitai, YAN Qiuhui. Analysis of thermal integrity of room air conditioner[J]. Journal of Refrigeration, 2013, 35(1):18-23.)
[2] SHEN Chao, CIRONE C, WANG Xinlei. Uncertainty analysis: design of a fouling test device for the liquid-to-refrigerant heat exchangers[J]. Applied Thermal Engineering, 2015, 85(6):148-159.
[3] 单元式空气调节机:GB/T 17758—2010[S]. 北京:中国标准化出版社, 2010. (Unit air conditioner:GB/T 17758—2010[S]. Beijing: China Standardization Press, 2010.)
[4] 单元式空调器:JIS B8616—2015[S]. 东京:日本工业标准调查会, 2015. (Package air conditioners:JIS B8616—2015[S]. Tokyo: Japanese Industrial Standards Committee, 2015.)
[5] Performance rating of unitary air-conditioning and air-source heat pump equipment:ANSI/ARI 210/240—2008[S]. Arlington: Air Conditioning and Refrigeration Institute, 2008.
[6] SHOKRI V, ESMAEILI K. Comparison of the effect of hydrodynamic and hydrostatic models for pressure correction term in two-fluid model in gas-liquid two-phase flow modeling[J]. Journal of Molecular Liquids, 2017, 237:334-346.
[7] 罗惕乾. 流体力学[M]. 北京:机械工业出版社, 2017. (LUO Tiqian. Fluid mechanics[M]. Beijing: Mechanical Industry Press, 2017.)
[8] LI Tianyu. On the formulation of a 3-D smooth curved pipe finite element with arbitrary variable cross-section[J]. Thin-Walled Structures, 2017, 117:314-331.
[9] LI Tianyu. On the formulation of a pipe element for a pipe structure with variable wall thickness[J]. Ocean Engineering, 2016, 117:398-410.
[10] KEFAYATI G H R, HUILGOL R R. Lattice Boltzmann method for the simulation of the steady flow of a Bingham fluid in a pipe of square cross-section[J]. European Journal of Mechanics-B/Fluids, 2017,65:412-422.
[11] 滕琴, 杨冬冬, 田奇勇, 等. 送风风道均匀送风的设计计算[J]. 流体机械, 2003, 31(1):310-313. (TENG Qin, YANG Dongdong, TIAN Qiyong, et al. Design and calculation of air supply duct with uniform air supply[J]. Fluid Machinery, 2003, 31(1): 310-313.)
[12] 李素玲, 赵韩, 史敏. 实验室均匀送风风道设计的近似计算[J]. 流体机械, 2004, 32(2):39-40. (LI Suling, ZHAO Han, SHI Min. Approximate calculation of uniform air supply duct design in laboratory[J]. Fluid Machinery, 2004, 32(2):39-40.)
[13] 肖婷, 李林, 梅硕俊, 等. 变截面风管均匀送风的气流组织CFD模拟[J]. 湖南工业大学学报, 2016, 30(2):13-20. (XIAO Ting, LI Lin, MEI Shuojun, et al. CFD simulation of air distribution in uniform air supply with variable section air duct[J]. Journal of Hunan University of Technology, 2016, 30(2):13-20.)
[14] 周东一, 石楚平, 肖飚, 等. 一种新型低温送风口的设计与实验研究[J]. 制冷学报, 2008, 29(5):33-38. (ZHOU Dongyi, SHI Chuping, XIAO Biao, et al. Design and experimental study of a new type of low temperature air outlet[J]. Journal of Refrigeration, 2008, 29(5):33-38.)
[15] 张继东. 空气幕均匀送风风道优化设计及仿真[D]. 天津:天津大学, 2005. (ZHANG Jidong. Optimal design and simulation of air curtain uniform air supply duct[D]. Tianjin: Tianjin University, 2005.)
[16] KORNILOV V L. Current state and prospects of researches on the control of turbulent boundary layer by air blowing[J]. Progress in Aerospace Sciences, 2015, 76:1-23.
[17] 王友君, 穆广友, 姜海英, 等. C型地铁列车次风道出风均匀性研究[J]. 东华大学学报(自然科学版), 2015, 41(5):689-691. (WANG Youjun, MU Guangyou, JIANG Haiying, et al. Study on air distribution uniformity of secondary air duct of C metro train[J]. Journal of Donghua University (Natural Science Edition), 2015, 41(5):689-691.)
[18] 付祥钊. 流体输配管网[M]. 北京:中国建筑工业出版社, 2016. (FU Xiangzhao. Fluid pipeline network[M]. Beijing: China Construction Industry Press, 2016.)
[19] REN Guorui, LIU Jinfu, WAN Jie, et al. Measurement and statistical analysis of wind speed intermittency[J]. Energy, 2017, 118:632-643.
[20] 张忠斌, 黄虎, 杜垲, 等. 隔板装置对恒温水箱的性能影响分析(2)实验验证[J]. 太阳能学报, 2016, 37(3):651-657. (ZHANG Zhongbin, HUANG Hu, DU Kai, et al. Effect of baffle configurations on the performance of thermostatic water tank (Ⅱ) experimental verification[J]. Acta Energiae Solaris Sinica, 2016, 37(3):651-657.)
[21] HARRIS R I. The level crossing method applied to mean wind speeds from “mixed” climates[J]. Structural Safety, 2017, 67:54-61.
[22] 栾茹, 王佳. 送风速度对室内气流分布影响的数值模拟[J]. 制冷学报, 2007, 28(5):31-35. (LUAN Ru, WANG Jia. Numerical simulation of the influence of air speed on indoor air distribution[J]. Journal of Refrigeration, 2007, 28(5):31-35.)
[23] 蔡宁, 黄晨, 曹伟武. 大空间下送风分层空调的同步求解模型的研究[J]. 制冷学报, 2011, 32(3):42-47. (CAI Ning, HUANG Chen, CAO Weiwu. Study on synchronous solving model of air supply stratified air conditioner in large space[J]. Journal of Refrigeration, 2011, 32(3):42-47.)
[24] 测量不确定度评价与表示:JJF1059—2012[S]. 北京:中国标准化出版社, 2010. (Measurement uncertainty evaluation and expression:JJF1059—2012[S]. Beijing: China Standardization Press, 2010.)
[25] ZIRKEL-HOFER A, PERRY S, FAHR S, et al. Improved in situ performance testing of line-concentrating solar collectors: Comprehensive uncertainty analysis for the selection of measurement instrumentation[J]. Applied Energy, 2016,185:298-312.
[26] CHOIA M K, HUH H, JEONG S, et al. Measurement uncertainty evaluation with correlation for dynamic tensile properties of auto-body steel sheets[J]. International Journal of Mechanical Sciences, 2017, 130:174-187.
[27] RAMADAN M, KHALED M, HAGE H E, et al. Effect of air temperature non-uniformity on water-air heat exchanger thermal performance-toward innovative control approach for energy consumption reduction[J]. Applied Energy, 2016, 173:481-493.
[28] BLECICH P. Experimental investigation of the effects of airflow nonuniformity on performance of a fin-and-tube heat exchanger[J].International Journal of Refrigeration, 2015, 59:65-74.
[29] 吴小舟, 孙雪丰, 王沣浩. 辐射空调房间供暖期室内热环境及通风效率实验研究[J]. 制冷学报, 2017, 38(1):40-46. (WU Xiaozhou, SUN Xuefeng, WANG Fenghao. Experimental study on indoor thermal environment and ventilation efficiency in a radiant air conditioning room during heating[J]. Journal of Refrigeration, 2017, 38 (1):40-46.)
[30] YOU Wei, SHEN Jialei, DING Wowo. Improving wind environment of residential neighborhoods by understanding the relationship between building layouts and ventilation efficiency[J]. Energy Procedia, 2017, 105:4531-4536.
[31] CONG H Y, WANG X S, ZHU P, et al. Improvement in smoke extraction efficiency by natural ventilation through a board-coupled shaft during tunnel fires[J]. Applied Thermal Engineering, 2017, 118:127-137.

