例题选择的标准
彭凌云
例题几乎是每节数学课必需的。虽然教材上有例题,但不是每个例题都是好的,有些甚至是不妥当的,教师必须结合教学的实际,选择更好的例题。因此,如何选择例题,老师们常常伤透脑筋,总是花费很多时间寻找自己认为好的例题。那么,好的例题的标准是什么?我们有必要探讨,以便老师们在选择例题时尽快找到,或者自己也能够编制。
一、难度不大
不论是新课还是复习课,例题难度要小,不能选择难度大的题作为例题。这是因为课堂教学要关注绝大多数孩子的数学学习状况。如果太难,大多数孩子听不懂,久而久之,数学差生就出现了。可以说,相当一部分数学差生就是因为例题没学好造成的。因此,合理地把握例题的难度,使每个学生都能参与到学习中,这是值得老师们关注的一个问题。
例如,一年级左右的学习,小孩子在没学之前能够分清左与右,学了之后,反倒分不清了,这是什么原因造成的?老师们常出这样的题:如下图,2号左边是几号?右边是几号?
学生犯难了:自己有左右,到底如何去看2号的左边、右边呢?要区分好这一点,小孩子要反复试验,通过站一站、看一看、辨一辨才能分得清。
同样地,学生解题能力的形成与提高,不是靠难题训练出来的,而是靠思维方法的长期熏陶。因此,课堂不宜讲难题,而要多讲思考方法,要让学生独立思考,慢慢体会解题的奥妙。
二、思路灵活
新课中的例题是为熟悉新学知识服务的,但往往显得呆板,作用单一。因此,教师需要尽量选用既能巩固所学知识,又体现灵活思路的例题,才能引领学生从不同角度思考所学知识,发挥例题的价值。
例如,我国古代数学名著《算法统宗》中有如下问题:“远望巍巍塔七层,红光点点倍加增,共灯三百八十一,请问尖头几盏灯?”意思是:一座7层塔共挂了381盏灯,且相邻两层中的下一层灯数是上一层灯数的2倍,则塔的顶层共有灯()。
A.1盏B.3盏C.5盏D.9盏
这道题在数学总复习时可以选用。解题的方法既可用算术方法,也可用方程,还可以用画图、列举等方法。
设顶层灯的盏数是单位1,則381÷(1+2+4+8+ 16+32+64)=3。因此,选B。
当然,设顶层有x盏灯,则有
x+2x+4x+8x+16x+32x+64x=381。
解得x=3。
还可以这样想:381=3×127,127是质数。而381是7个数相加,且后一个数是前一个数的2倍,那么第一个数是后面每一个数的约数,所以第一个数是3。这种方法十分巧妙,教师在指导学生分析解题思路时,要告诉学生善于分析题中数据,也许能够发现意想不到的方法。
三、趣味多多
趣题一般是数学家创作的,背后有故事。孩子们大多都崇拜数学家。对这些趣题,他们容易产生解题的兴趣———我也来试试,看看自己的智慧。孩子们兴趣浓,积极性就高,思维自然就容易动起来,不会讨厌数学。
如教完路程、速度、时间这一内容后,教师可以给出题目:一个人带一只狗在1000米长的路上来回跑。人与狗同时从路的一端出发,人跑的速度是每分钟100米,狗跑的速度是每分钟300米。狗到达另一端后,立即返回,碰到人后又返回到另一端,如此继续跑下去,直到人到达另一端为止。在整个过程中,狗跑了多少米?
据说这是苏步青先生(文中第一幅像)在日本留学时,有人故意试试苏先生的题(数据有改动,意思一样的)。学生可以先独立思考,肯定难以解答。很多人想采用分段的方法算出狗跑的路程,然后相加。这样做的话,将是非常复杂的。实际上,要求狗跑的路程,已知狗跑的速度是每分钟300米,那只要知道狗跑的时间就行了。而狗跑的时间与人跑的时间是相等的,显然,人跑的时间是1000÷100=10(分钟),那么狗跑的路程是10×300=3000(米)。
又如,在讲三角形内角和是180毅时,大家都是采用剪、拼、量的办法。我们不妨试试下面拼的方法(如图所示),也就是用6个完全一样的三角形按图中的方式拼出来,容易知道内角和是180毅。这是公元前6世纪古希腊数学家泰勒斯采用的方法。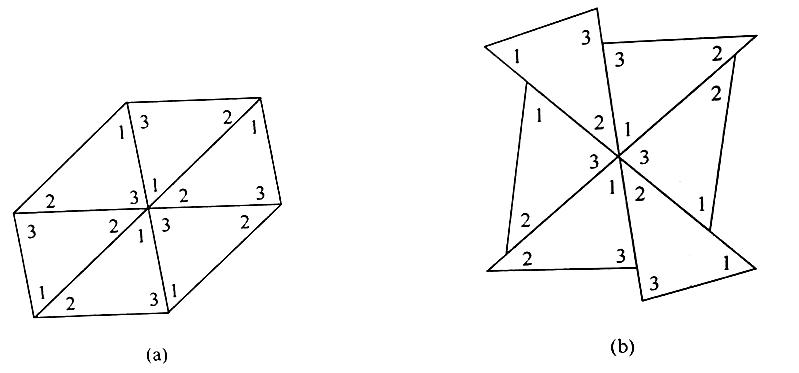
当然,还可列出一些标准来选择例题。如果按照上面的三条进行选择,选出的例题基本上是好的例题,我们的教学也会因此而更加生动、更加有效率。
(作者单位:长沙市岳麓区博才卓越小学)

