CAPM财务评估模型的参数研究

■崔 劲 豁秋菊

一、CAPM模型简介

CAPM模型（Capital Asset Pricing Model，资本资产定价模型）是在Markowitz均值-方差模型的基础上，由Sharpe等经济学家提出的资产收益率与风险在均衡状态下的关系模型，Markowitz与Sharpe因其研究获得了1990年诺贝尔经济学奖。

该模型认为，任何风险资产的均衡收益率都等于无风险收益率加风险溢价，用公式表示为：

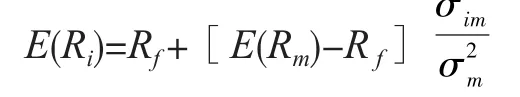
其中，E(Ri)为风险资产i的均衡收益率，Rf为无风险资产的收益率即无风险收益率，E(Rm)为市场投资组合的期望收益率，［E(Rm)-Rf］称为市场风险溢价，σim和分别是风险资产与市场投资组合之间的协方差及市场投资组合的方差。若令则上式变为：

由于CAPM模型是在一系列假设下推导出的数理经济模型，其中的参数都是理论抽象化的假设，使得CAPM模型的应用在国内外实务操作中都遇到了困难，如无风险收益率的选取、市场风险溢价的确定等，只有确定了这些参数才能通过CAPM模型得出折现率，进而完成资产的估值。

二、无风险利率的确定

在实证研究以及价值评估中，利用国债到期收益率作为无风险利率是最为常见且最为合理的。然而，从国债到期期限上来看，有短期国债（如30天）、中期国债（5年）、长期国债（10年、20年、30年等），选择何种期限的国债到期收益率作为无风险利率需要根据评估对象的具体情况来确定。

如果评估对象是一个短期投资项目，并预计到期以后套现退出，此时可以根据投资周期选择期限匹配的国债到期收益率，确定无风险收益率。

如果评估对象是一家持续经营企业或者一项长期股权投资，通常选择长期国债到期收益率作为无风险收益率并以此测算股权风险溢价。但在实际操作中，是选择10年、20年还是30年期的国债到期收益率，则需要谨慎研究。尽管不同期限的长期国债到期收益率之间呈现较为相似的走势（图1），但不同期限的收益率之间还是存在较为明显的差异（图2），而且期限差异越大，收益率差异也越大。

实际操作中，由于很难实现用各个期限的国债到期收益率及相应的市场风险溢价对各期现金流进行折现，因此一般可以估计企业未来净现金流现值发生的平均期间，并以此期限作为无风险利率及市场风险溢价的平均期限时间，即现金流持续期（或称“久期”）：

图1

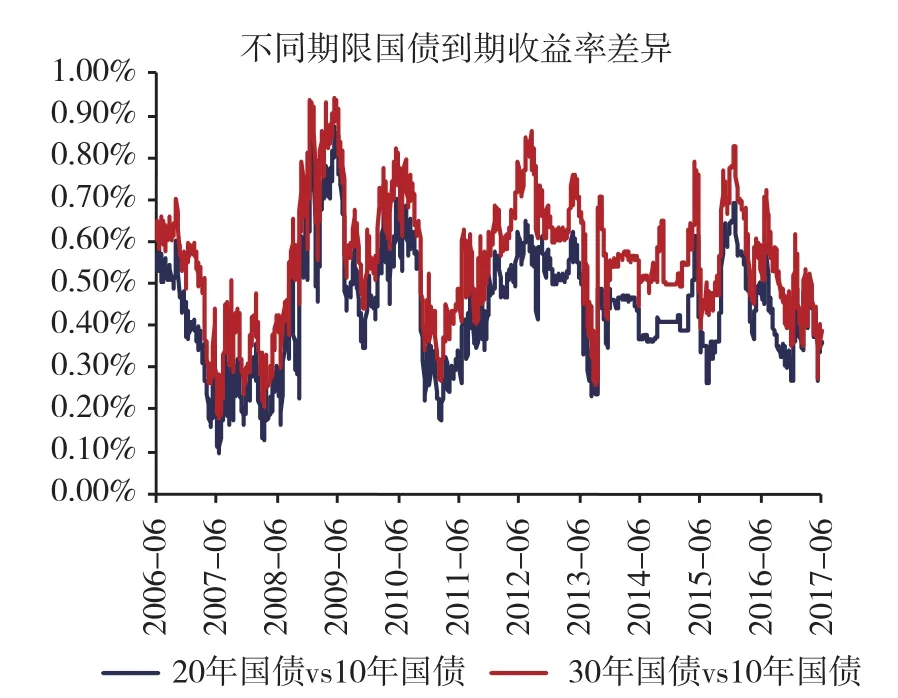
图2

其中，ct为各期现金流现值，p为各期现金流现值之和，即

例如，评估一家中国企业的持续经营价值时，假设评估基准日企业的现金流为100万元，且未来现金流将经历先快速增长后进入稳定的阶段，折现率为10%，企业可持续经营时间大约为100年（企业经营至第50年时，剩余各期现金流现值对整体净现值贡献十分微小）。在这样的假设前提下，该企业现金流现值之和为1,999.81万元，平均持续期为13.24年。若对折现率以及快速增长期的增长率作敏感性分析，可以得到不同的久期结果（表1）。

表1 久期敏感性分析

由表1可以看出，折现率越大久期越小，现金流增长率越高久期越大。另外，表1也基本反映了企业价值评估时现金流现值的平均发生时间，因为：第一，久期与评估基准日时点的企业现金流规模没有关系，不受企业规模大小的影响；第二，以EBITDA作为企业现金流的近似指标，可以发现2011-2015年中国全部A股的EBITDA平均增长率为9.56%，最高年份为13.27%，最低年份为6.37%，由此可以推断企业未来10年预期增长率大概处于6%～10%的范围；第三，中国长期国债到期收益率大约为3%，市场风险溢价大约7%，企业贝塔假设与市场波动相近，取值为1，则股权成本大约为10%；将1年期以上平均长期贷款利率作为债务成本，大约是5%。一般来说，公司权益市场价值大于债务市场价值。在这些假设条件下，中国企业的资本成本WACC（或折现率）取值范围大约是7%～10%，如表2所示。

表2 中国折现率取值

综上，若将企业未来10年增长率以及折现率分别限定在6%～10%和7%～10%左右的水平，那么企业未来现金流现值的平均发生期间大约是12-18年（如表3黄色填充部分）。进一步分析中国A股全部上市公司在2015年的资本结构可以发现，剔除数据缺失的样本，剩余的2,400家上市公司的股权市场价值占企业总体价值的比重大约在90%～95%左右，折现率的取值范围可以缩小至9%～10%，此时这个平均期限比较靠近10至15年（表3中红色虚线框部分）。换言之，10年期或15年期比较接近中国的股权资本投资平均有效期（久期），因此选择10年期或15年期国债到期收益率作为无风险收益率比较符合中国实际。

表3 中国的股权资本投资平均有效期（久期）

美国学者通常将国债到期收益率的期限选择为20年，我们依然可以从久期的概念出发，探寻使用20年的合理性。美国长期国债到期收益率约为2%，市场风险溢价在5%左右，同样假设企业贝塔趋近于1，则股权成本约为7%；美国1年期以上平均贷款利率约2%，即债权成本为2%左右，考虑到税率（约40%）的影响，则美国企业折现率取值范围是4%～7%，如表4所示。

表4 美国折现率取值

另外，美国2011-2015年上市公司EBITDA平均增长率为8.64%，最高年份为11.85%，最低年份为6.31%，推测企业未来预期增长率大概处于6%～8%的范围。综合美国企业收益增长率以及折现率取值范围，其未来现金流现值平均发生期间大约为16-26年，如表5黄色部分。进一步考察美国近3,700家上市公司在2015年的资本结构可以发现，美国上市公司权益价值占企业总体价值的比重大约为70%～75%，折现率的取值范围可以进一步缩小至5%～6%，此时现金流现值的平均发生时间更加接近20年（表5中红色虚线框部分）。因此，对于美国企业，选择20年期国债到期收益率较10年期的更加合理。

表5 美国的股权资本投资平均有效期（久期）

美国10年期与20年期国债到期收益率走势及差异如图3、图4所示，二者走势基本一致，但数值上存在较为明显的差异，因此选择适合的国债期限对无风险收益率的衡量非常重要。

图3

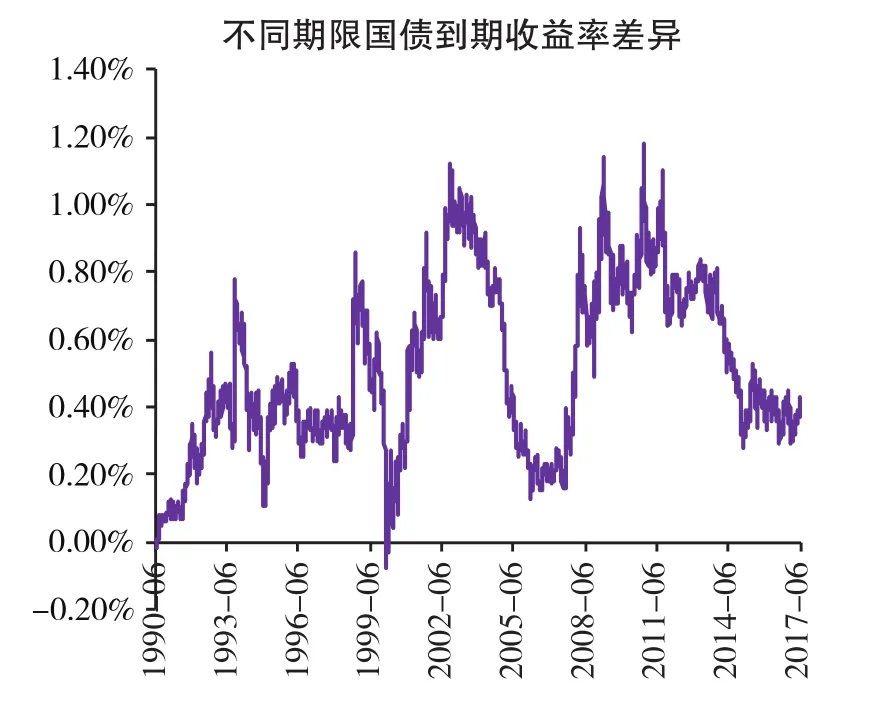
图4

三、市场风险溢价的确定

市场风险溢价是指市场期望回报超过无风险收益率的部分。理论界对市场风险溢价的研究，大都采用历史股票指数在一定时期内的平均市场收益率减去无风险收益率获得。我们对中国市场风险溢价的测算是在美国市场风险溢价的基础上调整而来：

中国市场风险溢价＝美国股票市场风险溢价＋中国股票市场违约贴息＝美国股票市场风险溢价＋中国违约补偿额×（σ股票/σ国债）

上述调整方法通常会遇到以下几个问题：一是为何不直接通过中国股票市场数据测算中国市场风险溢价；二是测算美国市场风险溢价时，数据期间及测算方法如何选择；三是中国股票市场违约贴息如何确定。

（一）通过发达国家数据进行风险溢价调整的原因

相较于发达国家的股市发展历史，中国股市成立时间较短。从各国指数的历史收益率来看，中国股市的波动较为剧烈，远未达到发达国家的稳定程度。

1. 美国股市收益率走势

美国在1927-1945年之间经历了历史上最为严重的经济大萧条和二次世界大战，股市表现出了较为明显的波动，如果剔除这段时期的影响，美国股市在近70年都较为稳定。

2. 加拿大股市收益率走势

加拿大股市与美国股市呈现相似特征，即1945年之前的一段时期股市波动较大，之后则较为稳定，加拿大股市成立时间较早，同样也受到了二战的影响。

图5

图6

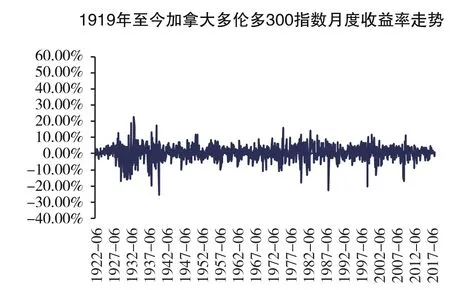
图7

图8

3. 欧洲（德、英、法）及日本股市收益率走势

欧洲股市起源很早，如英国股市起源于17世纪末，但发展初期均经历了股票交易品种少，股市不够成熟、交易不活跃的局面，之后两次世界大战以及世界金融危机更使欧洲股市受到重创。二战之后，欧洲股市进行了一系列的金融政策和股票市场改革，才有了现在的成熟与稳定（图9、图10、图11）。

相较于欧洲，日本股市发展较晚，在20世纪70年代以前，日本证券市场发展缓慢，之后日本金融国际化促进了日本证券市场的迅速发展，股市不断趋于成熟、稳定（图12）。这说明一国股市的稳定性与其股市发展的成熟度有关，也与该国经济的发展程度密切相关，需要经历较长时间的市场考验。

图9

图10

图11

图12

综上可以看出，无论是美国、加拿大还是欧洲、日本，其股市在成熟稳定之前都经历了相当长的发展与改革过程，之后才保持一种相对稳定的态势。中国作为新兴市场国家，虽然经济总量位居世界前列，但经济发展程度或发达程度与上述主要发达国家之间还存在显著差距，中国股市发展至今也只有20多年，目前仍处于不成熟、不稳定阶段，波动较大。

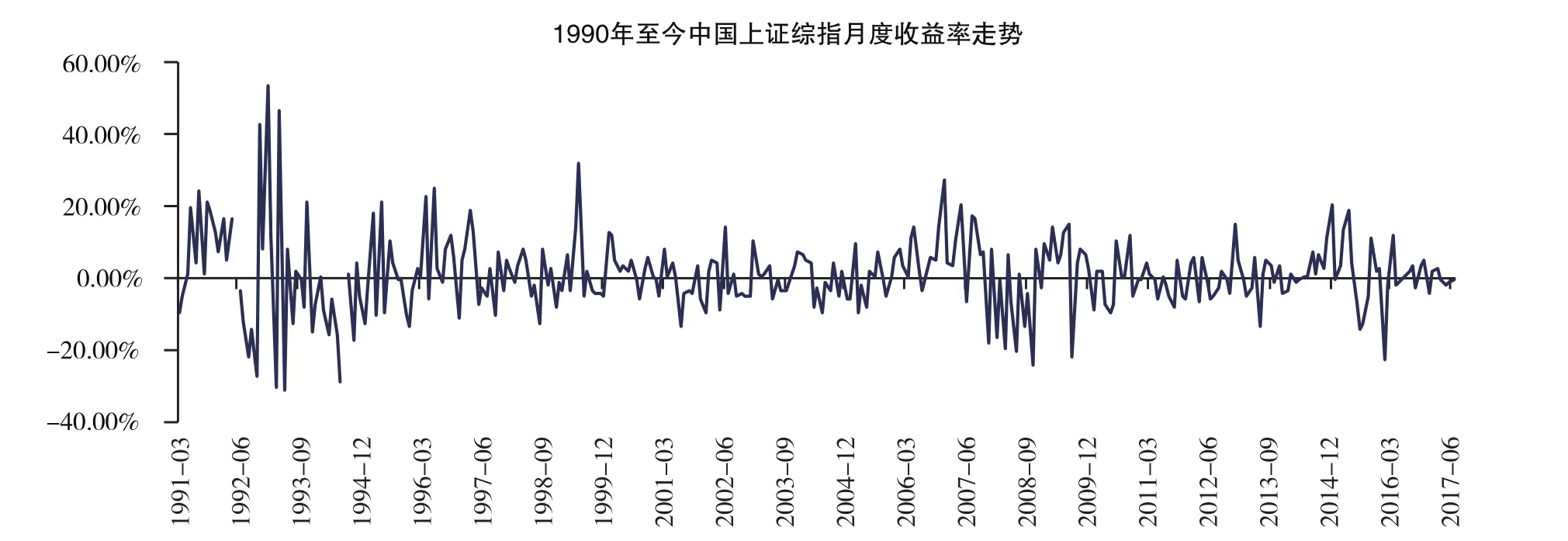
图13

上述各国股市收益率的走势图从直观上表明中国股市的波动率远远大于发达国家。再由各国历史收益率的波动数据（方差）来看，无论是否剔除经济大萧条及二战对发达国家股市的影响，中国的波动率都远远大于这些国家，波动率平均数值是发达国家的3倍左右。

表6 未剔除发达国家受经济大萧条及二战时期的影响之前

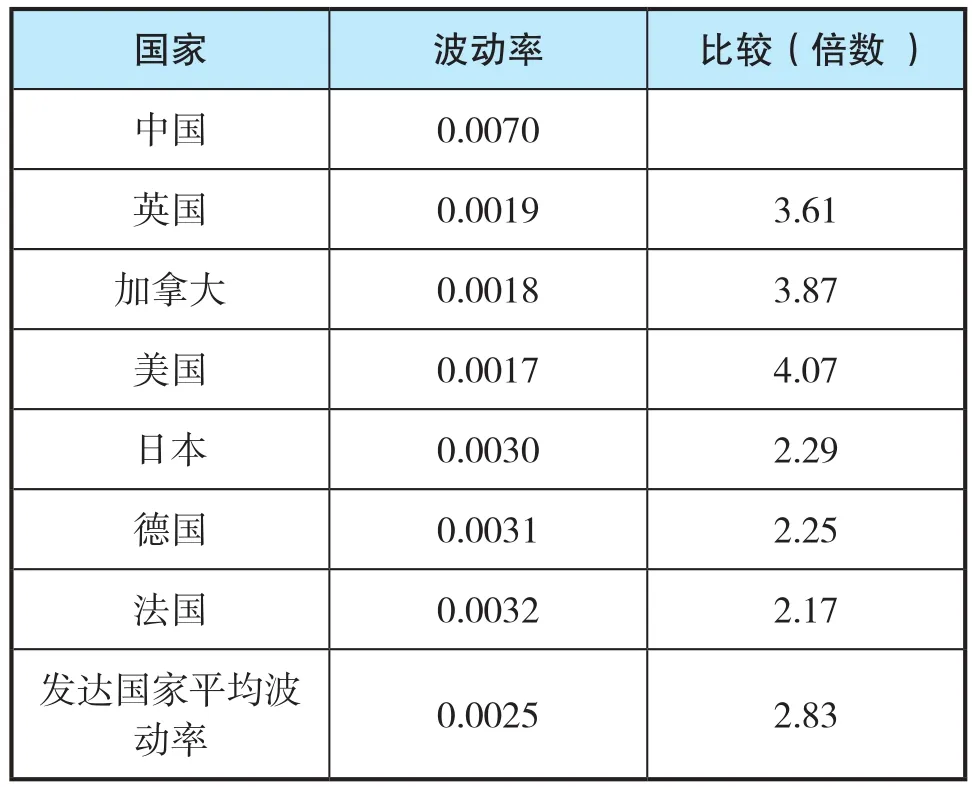
表7 剔除发达国家受经济大萧条及二战时期的影响之后

由上述分析可以看出，中国股市的成熟程度远远低于发达国家，因此直接利用中国股市的历史数据测算市场风险溢价并不能够准确反映市场未来的收益率及风险，用来作为折现率的输入参数去对未来现金流进行折现也是不合理的。美国作为发达国家的代表，在国际资本市场中常被作为基准国对其他国家的收益及风险进行衡量，所以选择通过美国的市场风险溢价调整得到中国的市场风险溢价是相对合理的。

（二）美国市场风险溢价的测算

1. 历史数据期间的选择

市场平均收益率（或市场风险溢价①如未特别说明，美国市场平均收益率及市场风险溢价的测算采用的都是SP500指数。）的测算对所选历史数据的时间区间非常敏感（表8），因此选择合适的数据区间对合理反映市场预期收益至关重要。

表8 市场平均收益率（或市场风险溢价）

一般来说，所选数据时段越长越好，无论是从统计意义还是从经济意义上来说，数据时段越长，观察样本越多，就越能够平滑少数极端值对最终结果的影响，收益就越稳定，进而会更加准确地反映市场实际收益水平。美国股市从1926年起即有交易数据，且其发布和现在的SP500发布方式是一致的，尽管如此，选择1926年作为起始点测算市场平均收益率仍然存在不妥之处：

第一，1929-1935年美国经历了历史上最为严重的经济大萧条，该时期产能过剩，消费降低，经济极度萎缩。

第二，1939-1945年属于二次世界大战时期，全球经济及股市均遭受了不可估量的重创。

第三，美国在1942-1951年经历了一段异常低利率（长期国债收益率远低于通货膨胀率，1949年除外）的时期：二次世界大战期间，美国财政部为了减少财政成本，人为地将利率控制在较低的水平，这一现象直至1951年4月才被消除。较低的债券收益率会导致更高的股权收益率。

因此，利用SP500测算市场平均收益率或市场风险溢价，最佳起始点应当是1951年之后，此后利率实现市场化，美国经济及股市都表现出长期的稳定性（表9），我们将测算市场平均收益率及市场风险溢价的起始点定在1952年。

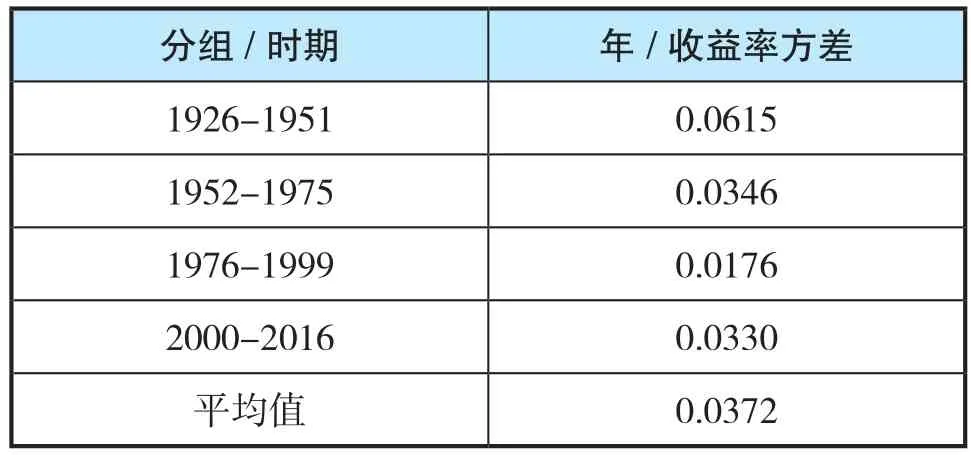
表9 美国市场波动性

2. 美国市场测算结果

对美国2015年以来的市场数据进行测算，得到各基准日的美国市场风险溢价，如表10所示。

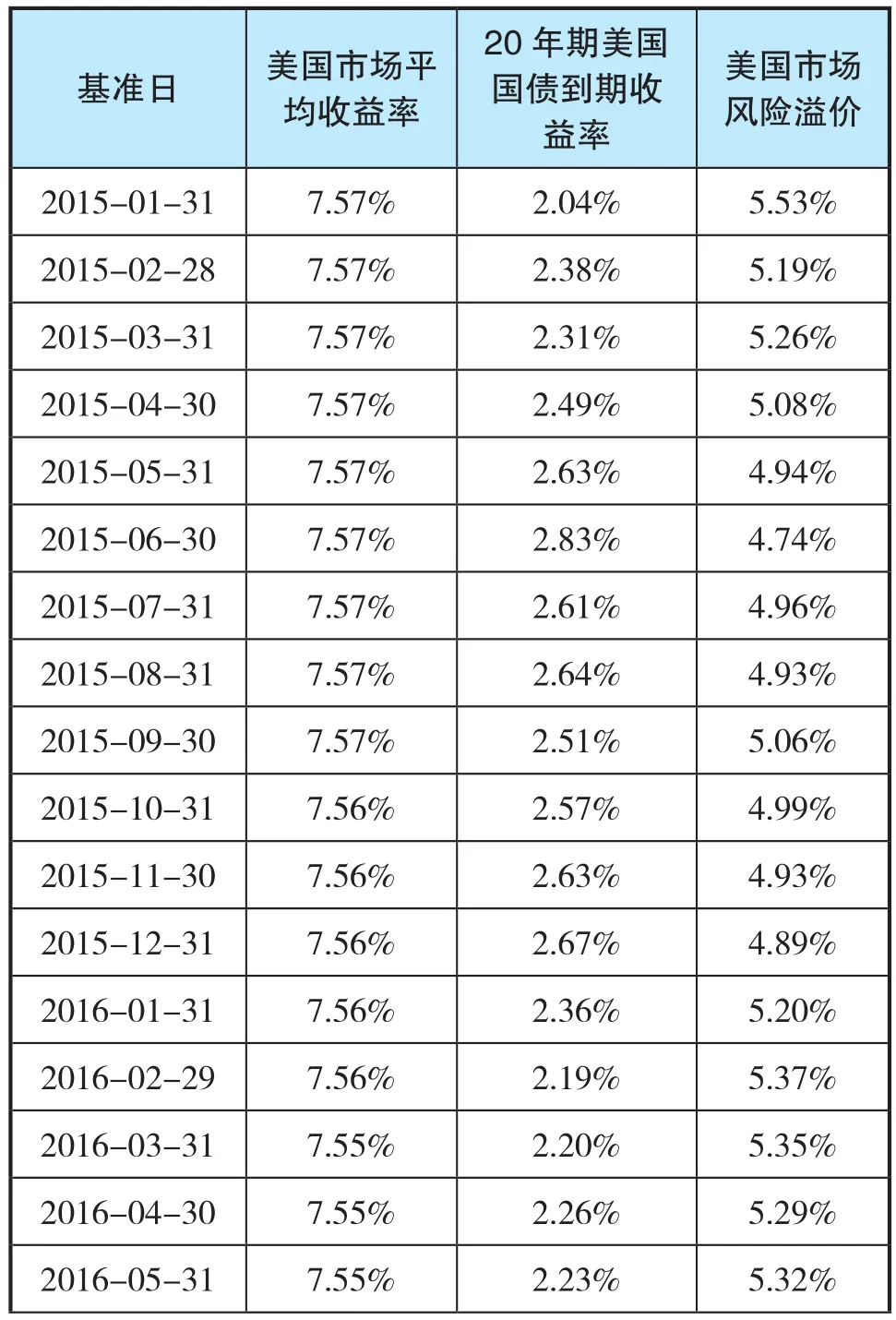
表10 美国市场风险溢价

续表

（三）中国市场违约贴息的测算

目前直接测算股票市场违约贴息尚没有成熟的做法，一般通过债券违约补偿额进行股票市场风险调整（σ股票/σ国债）进行测算，国际上有权威评级机构（如穆迪、标普）对各国政府债券进行评级，由此可以获得债券违约贴息额。

对于σ股票/σ国债的取值，国外学者常用1.5倍表示股票波动相对债券波动的程度，目前这一比值也被广泛应用于中国市场。然而，我们认为1.5倍或许不能够准确地反映中国股票波动风险相对债券波动的程度，因为：

第一，1.5倍是以几十个新兴市场国家为研究对象，反映的是新兴市场国家股票市场波动相对债券市场波动的平均水平，而中国经济体量与运行方式与普通新兴国家有很大差异，中国股市相对债券市场的实际波动程度也有其特点；

第二，股票市场及债券市场会随着经济结构变化而发生变化，股票市场相对债券市场的波动程度同样会发生变化，而保持1.5倍一直不变就无法反映股票市场和债券市场随经济周期变化而发生的合理变动；

第三，国外学者在测算这一比值时，股票市场与债券市场的波动程度采用的是短期数据（如2年），较短的数据时段难以有效反映股市和债市在稳定发展时期的合理波动水平。

因此，我们有必要研究中国自身的股票市场相对债券市场的波动程度。

中国股市在成立之初（1993年之前）波动较大，中间经历了2007-2009年的金融危机以及2015年的股市大涨和暴跌，如图14所示。

为避免股市大涨大跌对其波动风险的衡量，可以剔除这段时期的影响，重新考察股市相对债券波动的程度，如表11所示。

图14

表11 中国股市与债市波动性

由表11可以看出，不管是否剔除股市剧烈波动时期的影响，中国股市的波动程度相对债券市场的波动程度都远远大于1.5倍。由于σ股票/σ国债反映的是股市和债市在运行相对稳健时期二者的风险比较，经济正常的周期性波动二者的相对波动程度影响较小，因此我们认为近期使用2.3倍对于中国市场来说是更为合理的选择。基于上述分析结果，中国市场风险溢价水平测算结果如表12所示。

表12 中国市场风险溢价

续表

四、研究结论

通过本文对无风险收益率及市场风险溢价的研究，可以得出以下几个结论：

第一，通过对企业未来现金流净值平均发生时间（久期）的研究发现，对于中国市场来说，选择10年期或15年期国债到期收益率作为无风险利率比较符合中国企业的实际，而对于美国市场，无风险收益率的确定，选择20年期国债的到期收益率则更为合理。

第二，中国股票市场与发达国家相比，还存在较大的差距，这一差距不仅仅是股市成立时间，更多的是一国的经济发展成熟度，中国股市的频繁波动性使得直接利用中国股票市场数据测算中国市场的风险溢价是不合适的，而通过成熟国家（如美国）的市场风险溢价进行调整获得则更为合理。

第三，美国在1951年之前经历了经济大萧条、二次世界大战以及异常低利率等重大事件的影响，将测算市场平均收益率（或市场风险溢价）的起始点定在1951年之后更为合理。

第四，在利用美国市场风险溢价调整计算中国市场风险溢价的过程中，中国股票波动相对债券市场波动的程度应该结合中国金融市场实际情况，剔除股市剧烈波动时期的影响，中国的股市风险大约是债券市场风险的2.3倍。