作商法、作差法与二元函数

安徽省肥东县第一中学 郑金成

近年来，高中试题常出现以大学知识为背景的情况。二元函数是微积分中的常见内容，有时它也会改变面貌出现在高中习题中。笔者认为，在解决这一类问题时，如何将二元函数转化为一元函数是关键。通常可以用换元法，将两个变量的商或差进行整体换元是解决这类问题的有效方法。本文就以笔者见到的一些蕴含二元函数知识的习题为例，来谈谈应对这一类题目的方法，仅供大家参考。

例 1、已知

（1）是否存在 x0∈R+，使 F（x0，2）=2？请说明理由；

（2）若对任意的 x，y∈R+，恒有 F（x，y）≥0，请求出a的取值范围。

解：（1）略。

（2）转化为求二元函数的最小值问题。

方法1：（巧用基本不等式）考虑到所以有，所以

当分子或者分母的系数发生改变时，例如改为即可。

方法2：（将二元问题转化为一元问题） 因 为 x，y∈R+， 故，令，则有：于是，二元函数就转化为一元函数的问题了，这个方法也是笔者在本文中强调的方法。接下来可以通过将分子进行配凑成2+4t的形式用基本不等式求最小值；也可以用求导的方法来解决，这里就不再赘述了。

例2、（2011年合肥市高三第三次教学质量检测理21）已知函数f（x）=（x+k）lnx（k是常数）。

（1）若f（x）是增函数，试求k的取值范围；

（2）当k=0时，是否存在不相等的正数a、b，满足。若存在，求出；若不存在，说明理由。

解：（1）略。

（2）k=0时，不妨假设存在 a＞b＞0符合题意，即

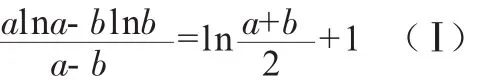
这是一个含有两个变量的方程式，如何将上式转化为只含有一个变量，即将其整理为关于的方程式成了解决该题的关键，有了这个意识后，这道压轴题就迎刃而解了，具体操作步骤如下：

上式转化为

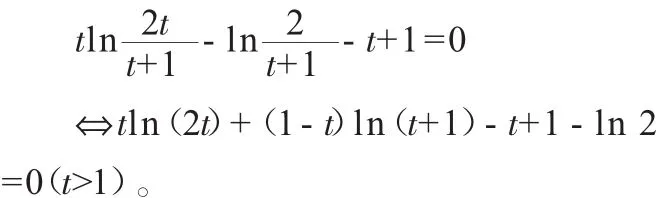
构造函数g（t）=tln（2t）+（1-t）ln（t+1）-t+1-ln 2（t＞1），这样就将原问题转化为了一元函数 g（t）在（1，+∞）上有没有零点的问题，接下来对g（t）进行求导判断单调性即可，属于高中生能解决的范畴。

这是一道学生课下问的习题，本题需要设出P、Q两点的横坐标，是一个二元问题，该学生的盲点就是不知如何将二元问题转化为一元问题。

解：设P、Q两点的横坐标分别为x1和 x2，且 0＜x1＜x2。

假设C1在点M处的切线与C2在点N处的切线平行，

令

上式转化为

构造函数则h（′t），所以 h′（t）在（0，1）上单调递减，所以 h（t）＜h（1），t∈（0，1）所以方程（Ⅱ）在（0，1）上无解，原问题得到证明。

[1]蔡小雄.孙惠华.新课标高中数学竞赛通用教材（高二分册）.浙江大学出版社，2013.7.