气隙尺寸对高压异步电动机磁场及性能的影响

，,,

(卧龙电气南阳防爆集团股份有限公司，河南南阳 473008)

0 引言

对于大、中型高压异步电动机而言，气隙尺寸的选取对电机设计至关重要，通常气隙尺寸希望选取的小一些，以降低空载电流，提高功率因数；但气隙过小，除影响机械可靠性外，还会使谐波磁场及谐波漏抗增大，导致最大转矩减小。而增大气隙后，随着气隙磁导的变小，谐波磁场的作用会减弱，附加损耗、电磁力均减小，对削弱电磁噪声也有一定的好处[1-4]。

然而，应用传统路法并不能精确地计算出气隙尺寸对电机内磁场、电机参数特征量及性能的影响。时步有限元法可以充分考虑到齿槽效应、饱和效应等影响电机性能的各种因素，从而准确获得气隙磁场分布，为分析气隙尺寸对电机性能的影响提供有效的计算方法。本文以一台高压异步电动机为例，首先通过建立二维场-路耦合的电机数学模型和物理模型，其中磁场与外电路采用直接耦合方式，对具有不同气隙尺寸(单边气隙分别为2.5mm、3.0mm、3.5mm、4.0mm)的电机进行了时步有限元分析，从理论分析和数值仿真两个角度详细分析气隙尺寸对电机气隙磁密分布、电机运行性能以及电机附加损耗的影响，对比分析了电机参数随不同气隙尺寸的变化趋势，所得结论为合理的选择气隙尺寸提供了一定的理论依据。

1 电机二维全域电磁场模型

1.1 高压异步电动机的模型及基本数据本文研究的高压异步电动机，基本数据见表1。

表1 高压异步电动机基本数据

为了研究不同气隙尺寸对电机性能的影响，同时考虑电机端部结构的复杂性，为减小计算模型尺寸及有限元剖分数量，本文分别建立了单边气隙分别为2.5mm、3.0mm、3.5mm、4.0mm时电机的二维电磁场计算模型，如图1所示。

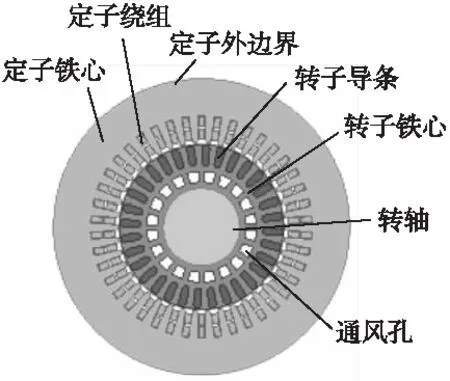
图1 高压异步电动机二维电磁场计算模型

图2 高压异步电动机剖分图

1.2 电磁场的基本方程

首先建立场-路耦合时步有限元模型，磁场与电路直接耦合，端部效应以端部阻抗的形式在外电路中予以考虑，根据求解条件及要求给出如下假设[5]

(1)铁心轴向有效长度内的电磁场按照二维场来处理，计算模型中定、转子内外边界的漏磁忽略不计；

(2)忽略位移电流及其影响，忽略电网电压中的高次谐波分量及定子绕组中的集肤效应；

(3)不计相间和槽间绝缘的影响；

(4)材料为各向同性，材料的磁导率均匀且不计磁导率随温度的变化；

(5)忽略磁性槽楔的导电性，不计由此产生的电气损耗。

基于上述文中假设，在计算的二维场中，由矢量磁位AZ表示的电机二维瞬态电磁场的边值问题为

(1)

式中，AZ—磁矢位；JZ—传导电流密度；μ—磁导率；σ—电导率；t—时间。

将式(1)依据变分原理化为条件泛函方程，然后对条件泛函方程离散化，在满足相应边界条件的基础上对多元方程组进行求解。在实际求解时，为了提高计算精确度，对不同的区域采取不同的剖分精确度，高压电机的剖分图，如图2所示。

2 气隙为不同数值时对电机气隙磁场的影响

当电机旋转运行时，定、转子齿槽相对位置是不断变化的，而随着气隙尺寸的改变，气隙磁导也会相应发生变化，磁动势的变化势必会影响气隙内磁密分布和磁密数值的改变[6、7]。本文分别对不同气隙尺寸电机内电磁场进行了有限元数值计算，并对气隙磁密进行了提取以及数值的傅里叶分解，单边气隙为2.5mm、4.0mm时气隙磁密值如图3所示。

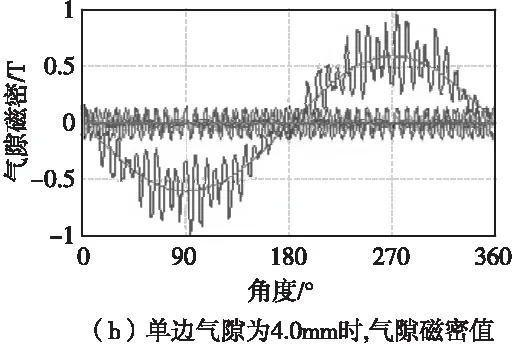
图3 不同单边气隙时，电机内气隙磁密值

由图 3(a)、图3(b)可见，具有不同单边气隙时的电机内气隙磁场数值波动大小不一，单边气隙为2.5mm时电机内磁场数值波动较大；伴随着气隙尺寸的增大气隙磁密分布波动幅值明显减小，这表明气隙磁密由于齿槽存在而产生的磁密不均匀现象得到了改善。由图 3(a)、图3(b)还可得出，当单边气隙为2.5mm时气隙磁密的最大值为1.24T，单边气隙为4.0mm时气隙磁密的最大值为0.98T；而相比于气隙4.0mm，气隙为2.5mm时气隙磁场的谐波含量较为丰富，这是由于气隙愈小气隙磁导相对越大，高次谐波磁势产生的气隙谐波磁场也越明显，高次谐波磁场的数值也就越大。

为了考察不同气隙时电机谐波含量的分布，给出了单边气隙为2.5mm、3.0mm、3.5mm、4.0mm时电机内气隙磁密的数值分解，如图4所示。

图4 不同单边气隙时，电机内气隙磁密的谐波含量

由图4可以看出，随着气隙尺寸的增加基波磁密值略有降低，而定、转子一阶齿谐波磁密值随着气隙尺寸的增加降低的速度较明显。

为了更加直观的分析不同气隙尺寸对电机气隙磁场的影响情况，本文通过对气隙磁密值进行了数学的傅里叶分解，定量的分析了不同气隙对电机内气隙磁密的影响，分析数据见表2。

表2 不同单边气隙时，电机内气隙磁密谐波含量幅值/T

由表2中的数据可知，单边气隙为3.0mm、3.5mm、4.0mm的电机额定负载运行时，气隙磁密基波幅值较气隙为2.5mm时分别降低了0.71%、1.58%、2.22%；相比31次转子齿谐波磁密幅值分别降低了9.55%、18.72%、28.27%，33次转子谐波磁密幅值分别降低了9.79%、10.85%、15.21%；而41次定子齿谐波磁密幅值分别降低了10.68%、20.57%、27.42%，43次定子齿谐波磁密幅值分别降低了11.02%、21.81%、29.88%。

由以上数据可知，随着气隙尺寸的增大，电机内气隙磁场的谐波含量整体有降低的趋势，其中定、转子齿谐波磁密幅值降低的尤为明显，但同时基波幅值也略有下降。而气隙中的谐波磁场一直是产生附加损耗、噪声、振动的主要因素，增大气隙尺寸可以有效改善气隙磁密分布，降低谐波磁密幅值，从而电磁噪声和振动会得到大的改善。因此，合理的选择气隙尺寸，对改善电机内磁场的分布及降低谐波含量有重要作用。同时，由气隙磁密谐波分解可以得出各次齿谐波磁密幅值，是准确计算电机损耗、性能参数的基础。

3 不同气隙对电机损耗、性能及电磁力波的影响

3.1 对电机表面损耗的影响

定子开槽引起的气隙磁导齿谐波磁场会在转子表面产生表面损耗，反之也是。由电机定、转子铁心开槽导致的气隙磁导不均匀，会在气隙磁场中产生大量的谐波，而谐波是产生铁心附加损耗的主要原因，包括表面损耗和脉振损耗。本文对比计算 了当电机气隙尺寸变化时的铁心表面附加损耗。由于定子开槽在转子表面形成的损耗为[8]

(2)

式中，t1、t2、b02—定子齿距、转子齿距、槽口宽；Z1、D2、lt2—定子槽数、转子铁心外径、铁心长度；B01—定子开槽引起的齿谐波磁密幅值，由有限元计算所得气隙磁密谐波分解求得。

计算不同气隙长度时电机转子表面损耗如表3所示，由文中的谐波傅里叶分解可知定、转子的二阶齿谐波磁密幅值均较小，因此，转子的表面损耗分别只计算了一阶齿谐波时的对应数值。

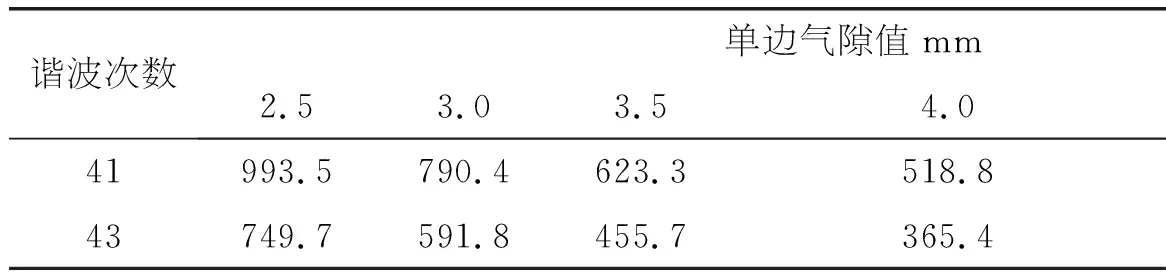
表3 不同气隙时转子表面损耗/W

需要说明的是，一般感应电机中，由于转子开槽，在定子铁心表面也会产生附加铁耗，在样机中，由于转子槽口尺寸为0，相对于气隙长度而言很小，因而忽略了由于转子开槽而在定子铁心表面产生的附加损耗。由表3可见，随着气隙尺寸的增大，电机转子表面损耗大幅下降，这是由于气隙增大后，减小了槽型对气隙磁场分布的影响，改善了气隙磁场的正弦度，从而减小了电机铁心表面损耗。

3.2 对电机铁耗、定转子焦耳损耗的影响

具有不同气隙尺寸电机额定工况运行时，电机内电磁场磁密分布及饱和程度的不同，不仅会对电机的铁耗产生影响；与此同时，磁密谐波含量、电流(包括谐波电流)的数值变化也会对定子绕组、转子导条的焦耳损耗产生影响；表4给出了不同气隙时，电机铁耗、定转子绕组损耗的变化情况。

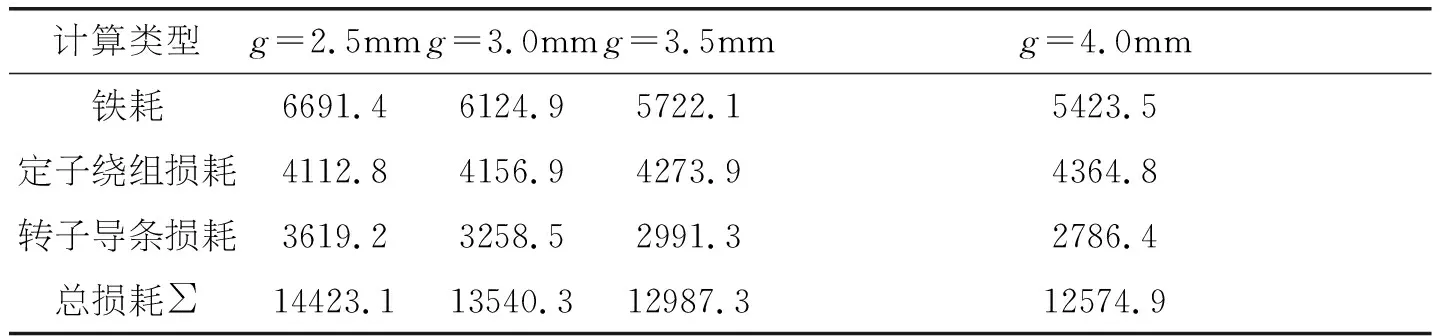
表4 不同气隙时，电机内损耗/W

由表4可得，随着电机气隙尺寸的变大，铁耗值减小，这是因为气隙变大电机铁心内磁密(包括基波、谐波)值降低所导致的。相应的定子绕组焦耳损耗随着气隙的变大，数值上略有增加，但是损耗数值增长的速度却不快(相比铁耗而言)，原因是随着气隙的变大，一方面功率因数降低，会导致定子电流增大，另一方面气隙变大定子电流谐波含量也相应降低。转子导条的损耗值随着气隙的变大，降低的也相对明显。而以上三项总损耗，随着气隙的变大降低的较明显。因此，在功率因数、电机的性能方面满足用户要求的情况下，合理的选择并放大气隙尺寸，对电机的损耗、发热会带来好处，从而延长电机的使用寿命。

3.3 对电机性能的影响

不同气隙尺寸的变化对电机性能的影响如表5所示。

表5 不同气隙时，电机性能指标

由表5可知，随着气隙尺寸的变大，电机的起动电流、起动转矩值略有降低，但降低的幅度较小。而功率因数随着气隙的变大，降低的的幅度较为明显，数值上影响较大。与此同时，额定电流值也会随着气隙的变大有增加的趋势，但电流数值的变化程度会受到电机效率、功率因数的影响[9，10]。

3.4 对径向电磁力波的影响

对于功率较大的高压异步电动机而言，振动和噪声也是倍受关注的问题。振动和噪声不但影响电机本身的使用寿命、也影响其拖动设备的工作质量和效率，同时也严重的污染了人们的生活环境并对人体造成危害。

电磁噪声是电机运行过程中定、转子磁场相互作用产生的一系列电磁力波引起定、转子铁心振动而产生的。不同气隙尺寸的选择可以有效的抑制电磁噪声。

根据麦克斯韦应力张量法，得出作用在电机定子或转子上的径向力密度和切向力密度为[11、12]

(3)

(4)

其中，引起电机振动和噪声的主要是电磁力的径向分量。根据式(3)计算电机负载运行时，不同气隙尺寸下电机一对极下电磁力波分布对比如图5。

图5 不同气隙时，径向电磁力密度

由图5中的数据得出，单边气隙为2.5mm、3.0mm、3.5mm、4.0mm电机额定负载运行时，径向电磁力波的幅值分别为4.9×105N/m2、4.3×105N/m2、3.9×105N/m2、3.6×105N/m2；相比2.5mm气隙时，气隙为3.0mm、3.5mm、4.0mm电机内径向电磁力波幅值分别降低了12.2%、20.4%、26.5%。由此可以看出，随着气隙尺寸的增大，可以有效降低电机运行时的径向力波的幅值，从而对优化电机的电磁噪声和振动起到非常好的效果。

4 实测数据与计算结果的比较与分析

基于场-路耦合时步有限元法对所建的电机的数学模型进行求解，可以获得样机稳态工况运行时的性能参数及起动性能的计算值。气隙为2.5mm时，样机的额定运行时定子额定电流、起动时的定子电流、起动转矩计算值及实测值，如表6所示。

表6 样机稳态运行参数计算值和实测值

由表6可知，定子额定电流计算值与实测值的误差为-2.0%，定子起动电流计算值与实测值的误差为3.7%，起动转矩值与实测值的误差为-4.26%。由此可知计算值与实测值比较接近，计算值与实测值的误差小于5% ，满足计算精度的要求验证了所建模型的准确性。

5 结语

通过场-路耦合的时步有限元法，定量分析了不同气隙尺寸对电机内气隙磁场、电磁力波、损耗及性能的影响。计算结果表明，随着气隙尺寸的增大，可以有效的改善气隙磁密的分布、减小了谐波含量、降低了表面损耗和减小径向电磁力。但是，随着气隙尺寸数值的增加，电机的功率因数降低的较明显，而起动转矩、起动电流略有降低，额定电流值略有增加。因此，在电机设计合理的选择气隙尺寸的过程中，必须综合考虑气隙尺寸对电机电磁参数和性能的影响，使电机产品性能达到最优。

[1] 电机内的电磁场[M]．北京：科学出版社，1998．

[2] 胡敏强，黄学良．电机运行性能数值计算方法及其应用[M]．南京：东南大学出版社，2003．

[3] 段晓田，张新燕，张俊，等.双馈风力发电机电磁场计算与分析[J].电网技术，2012，36(2):231-236.

[4] MIKAMI H，IDE K，ARAI K，et al. Dynamic harmonic field analysis of a cage type induction motor when magnetic slot wedges areapplied[J]. IEEE Transactions on Energy Conversion，1997，12(4):337-343.

[5] 梁艳萍，陈晶． 磁性槽楔对高压感应电动机电磁参数和性能的影响[J]． 电机与控制学报，2010，14(3) : 1-5．

[6] 李隆年．电机设计[M]．北京：清华大学出版社，1992．

[7] B. 海勒尔，V. 哈马塔. 异步电机中谐波磁场的作用[M]. 北京:机械工业出版社，1982.

[8] 李海成， 王庆东， 尹志华.中小型笼型异步电机杂散损耗的降低措施[J]. 电机与控制应用，2015，42(4):70-74.

[9] 严登俊，刘瑞芳，胡敏强，等．鼠笼异步电机起动性能的时步有限元计算[J]．电机与控制学报，2003，7(3)：177-190．

[10] 李军，刘颖，许自贵，等. 层压型磁性槽楔的性能及其对电机性能的影响[J]. 中国电机工程学报，2005，25(16):126-131.

[11] 王荀，邱阿瑞．笼型异步电动机径向电磁力波的有限元计算[J]. 电工技术学报，2012，27(7):109-117.

[12] 刘海龙. 大型感应电动机电磁力及振动特性分析[D]. 沈阳:沈阳工业大学，2007.