考虑相关性的串联系统动态机会成组维修优化

徐孙庆, 耿俊豹, 魏曙寰, 刘凌刚

(1. 海军工程大学舰船动力工程军队重点试验室, 湖北 武汉 430033;2. 海军工程大学动力工程学院, 湖北 武汉 430033)

0 引 言

多部件系统存在3种相关关系:经济相关性、结构相关性、随机相关性[1]。这些相关性的存在使得单部件的维修策略并不总是适合多部件的维修决策,因此机会维修被引进应用在多部件维修领域。文献[2]首先提出机会维修模型,文献[3]进一步分析了相关性对维修工作的影响,提出从时间相关性、故障相关性、结构相关性和功能相关性4个方面描述多部件系统的维修相关性。在多部件系统维修优化领域,成组维修已经被成功引进、发展、应用在一些机械系统,通过利用短期信息(部件故障或性能退化)改变原有维修计划,建立动态模型实现维修优化[4-6]。文献[7]提出动态分组的模型,使维修能够实时更新,但是根据文献[8]研究,该模型的成立受限于维修时间可忽略且在规定时间内任一部件至多进行一次预防性维修的假设。为了解决上述问题,文献[9-10]对该模型进行了拓展,但维修资源的限制还未进行考虑。由于动态规划的方法不能很好解决分组过程的非确定性多项式(non-deterministic polynomial,NP)难问题,粒子群算法[11]、遗传算法[12]、蚁群算法[13]等被引进用于解决组合难题。在实际应用方面,文献[14-15]将滚动计划的动态机会维修策略应用于风电机组维修,但只考虑部件间的经济相关性。文献[16-23]对动态成组维修进行了系列研究,包括在可用度、维修资源、维修时间等方面的限制加以考虑的情况下,对不同的相关性模型进行维修优化研究,并且讨论了复杂系统结构的一些情况,推进了相关理论的研究。文献[24]对多部件的相关性模型加以研究,并用蒙特卡罗方法进行仿真,但样本数较少,且在单独考虑这种相关性时,现有的机会维修策略可能会导致次优的解决方案。文献[25]针对部件的3种相关性利用Gamma过程进行仿真建模。文献[26]以更新周期内平均维修费用最小为目标建模,并借助Matlab用枚举法加以实现。

系统部件大多处于一种动态变化的环境之中,现有文献研究基于无限时域的静态模型的较多,即使部分文献考虑了动态特性,但并没有考虑到部件间的多种相关性。因此,本文提出一种新的基于动态成组的经济、结构相关性维修模型,建立基于相关性的自适应的机会维修策略,将长期计划与短期计划相结合,从而能够依据最新的任务要求或系统状态更新维修方案,得到高效的维修计划。

1 相关理论

考虑由n个部件组成的串联系统,任一部件故障都将导致系统故障。由于多数故障的发生具有随机性,为了防止系统故障出现,制定维修策略时必须考虑对随机故障的处理,因此预防性维修与故障维修都是必要的维修手段。本文假设所有维修资源是充足的。

1.1 单部件维修费用

(1)

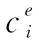
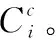
1.2 经济相关性

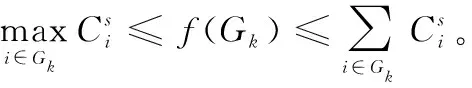
1.3 结构相关性

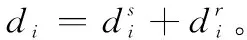
(2)

2 机会成组维修模型

相对于各部件单独维修费用之和,部件间存在的相关性使得成组维修的费用会少。为了寻找最优分组结构,得到最低系统维修费用,文献[4]引进了滚动计划,便于决策者能在长期计划的基础上依据新信息制定短期计划。本文进一步考虑维修时间的影响,提出将机会成组维修分为4个阶段进行实施,如图1所示。

图1 机会成组维修方法Fig.1 Grouping based opportunistic maintenance approach

首先根据各部件参数进行部件级优化,确定有限时域内各部件的维修间隔期及维修费用率;其次在此基础上制定试行维修计划,此时不考虑部件的相关关系;随后针对部件间的经济相关性和结构相关性构造模型,进行系统级维修优化,确定有限时域内最佳成组维修时间;最后根据新信息及滚动计划,实时更新维修计划,从而得到最佳维修方案。

2.1 阶段1:部件级维修优化

本阶段的目标是找到每个组件的最佳预防性维修周期。假设一个由n部件构成的串联系统,任一部件故障都将导致系统停机,各部件间的故障互相独立。以威布尔分布为例来描述组件的故障行为。部件i的故障率λi(t)为

(3)

式中,βi为形状参数;ηi为尺度参数。

记Ci(x)为部件i的维修费用。当部件i在时刻x发生故障,对其进行最小维修,则Ci(x)为

(4)

式中,λi(t)为部件i的故障率。由式(3)、式(4)得

(5)

如果部件i在x时刻进行预防性维修,则其在[0,x+dt]时段内的预期费用为

(6)

根据更新理论,部件i的平均维修费用如式(7)所示。

(7)

(8)

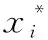
(9)

(10)

2.2 阶段2:试行维修计划

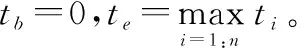
记ti1为部件i第一次维修时间为

(11)

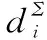
(12)

2.3 阶段3:系统级维修优化

本阶段的目标是为了寻找系统机会维修的最佳方案,从而使得总的维修费用最小。每次维修都是将一个组合Gk里的部件同时替换。每个组Gk同时维修节省的成本可划分为3个部分。

(1) 惩罚成本

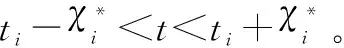
(13)

式(13)也可以表示为

(14)

记PGk(t)为成组维修的总惩罚费用,优化维修的时间记为tGk,此时PGk(t)取得最小值

(15)

(2) 拆装节省成本,记为S(Gk)

(16)

(3) 停机损失节省成本,记为D(Gk)

当多个部件的预防性维修工作同时进行,可减少系统的停机时间,从而使得总停机损失降低。

D(Gk)=Cu·g(Gk)

(17)

Gk的节省费用为

(18)

如果QGk>0,则称Gk为成本有效组。维修决策组合G1,G2,…,Gs是G的互斥子集,其中

(19)

2.4 阶段4:维修计划的动态更新

由于部件间存在经济相关性和结构相关性,可用本文方法利用相关性进行分组维修优化。对维修活动进行分组优化,意味着部件维修时间的提前或延后。同一分组里的所有部件同时进行维修活动,分组里部件的维修时间从阶段2单部件优化得到的维修时间提前或推迟至阶段3得到的成组维修时间,使系统的维修成本最小。

大多数成组维修模型是建立在无限时域的基础上,这些模型属于静态分析,无法根据新信息及时调整维修计划。在有限时域内,采用滚动计划的方法,阶段3得到的维修计划,可依据环境条件变化和计划执行情况,动态地调整维修计划和更新维修周期。此外,在一个计划周期结束时,新的维修计划与维修周期需要确定,因此重新返回阶段2确定各部件在新的维修计划周期内的维修时间。

3 遗传算法

求解n部件系统分组优化属于NP难问题,采用精确的方法去寻求n部件的所有分组结果会耗费大量时间,特别是当部件数量n较大时[27-28]。根据文献[29]研究,当部件数量为16时,应用动态规划方法求解,计算机计算运行时间将超过50天,而采用遗传算法仅需要86.07 s,由此可见遗传算法在处理多部件优化组合计算时的优越性,因此本文引进遗传算法进行优化分组求解。

遗传算法作为一种通用的搜索策略,经常被用于求解优化组合问题[30]。遗传算法的主要步骤包括编码、产生初始群体、个体适应度评估、选择策略、交叉策略、变异策略。本文编码采用数组表示,初始群体为100,交叉概率为0.80,变异概率为0.02,当迭代次数达到规定值4 000次时终止,以节省费用最高的组合作为最优解。

4 案例分析

以一个10部件的系统为例,其停机损失为1 000元/天,假设故障率服从两参数的威布尔分布,各部件参数如表1所示。

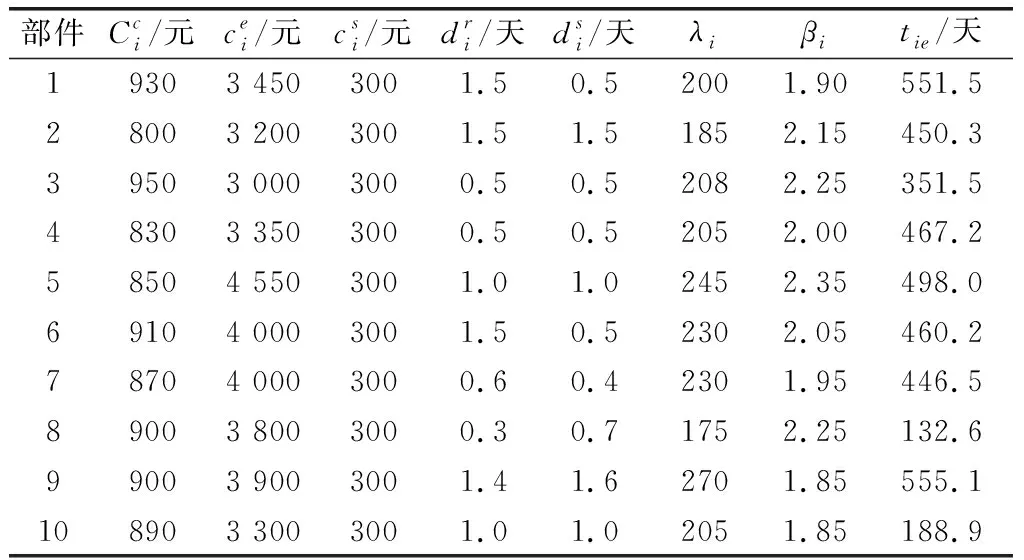
表1 系统各部件参数

4.1 部件级维修优化

当不考虑相关性时,根据式(9)、式(10)对系统各部件进行维修优化,可得各部件的最佳维修间隔时间、最小费用率及各部件维修时间,如表2所示。

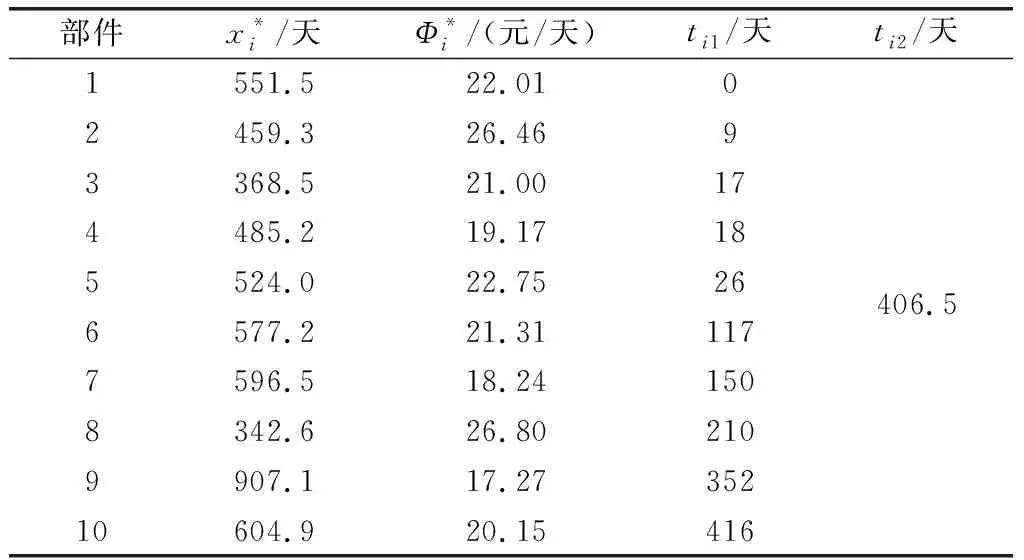
表2 单独维修优化值

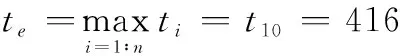
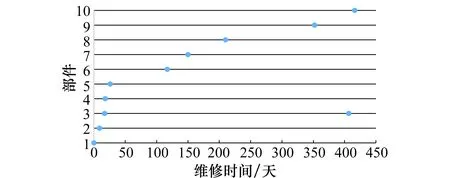
图2 各部件维修时间Fig.2 Maintenance time of each component

4.2 考虑相关性的系统级维修优化

考虑动态成组维修策略,运用遗传算法进行求解,所得优化分组情况如表3所示。

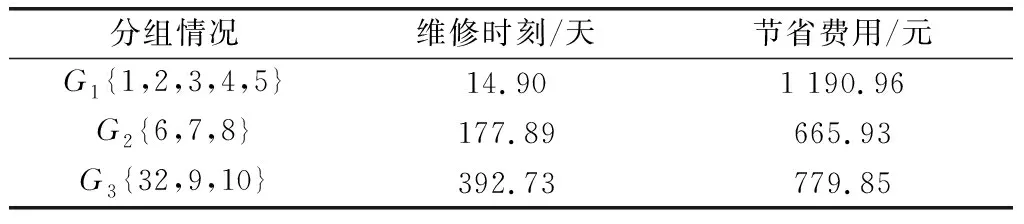
表3 只考虑经济相关性的优化分组

分组后维修时间如图3所示。

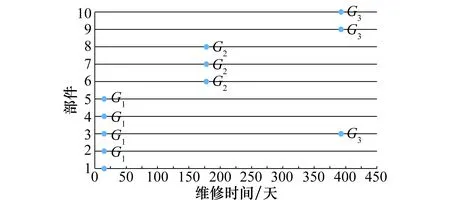
图3 分组维修时间Fig.3 Grouping maintenance time

图3描绘了不考虑结构相关性时分组维修的维修时间。由表3可得,仅考虑经济相关性时,与单独对部件维修优化相比,系统节省维修费用为2 636.74元,节省费用占原维修费用的2.95%。

由于结构相关性的存在,可使部件同时维修时所需的维修时间减少,从而降低维修费用,因此需同时考虑结构相关性与经济相关性时。表4、表5分别显示了不同结构相关性系数下节省维修费用、维修时间的数值。

表4 不同相关性系数下节省时间

综合表4、表5数据不难发现,部件间的结构相关性对维修时间的节省有较大影响,当且仅当部件间的结构相关性系数为50%时,应用本文方法可节省维修时间2.45天,与不考虑结构相关性相比,维修时间降低12.89%;从费用方面考虑,减少维修费用5 086.74元,与不考虑相关性情况相比,费用降低5.68%;与仅考虑经济相关性的情况相比,也即结构相关性系数为0时的情况相比,维修费用较仅考虑经济相关性的情况又降低了2 450元。

表5 不同相关性系数下节省费用

为了更加直观的展示相关关系,图4、图5描绘了系统部件的结构相关性系数与维修节省时间、维修节省费用的关系。

图4 不同结构相关性系数下节省时间Fig.4 Saving time with different dependence parameter

图5 不同结构相关性系数下节省费用Fig.5 Saving cost with different dependence parameter

结构相关性系数为0可代表仅考虑经济相关性的情况,从图4、图5中不难发现,随着部件间的结构相关性系数增加,节省的维修时间与维修费用也随之增加。同时考虑经济相关性和结构相关性的情况下,当结构相关性系数为0.9时,节省费用为7 046.74元,与只考虑经济相关性节省的2 636.74元相比,又减少了4 410元,而且维修时间减少了4.41天。若只考虑经济相关性可能得到次优的维修计划,因此将结构相关性也加入到组合策略中,才能得到更科学的维修策略。

5 结 论

本文同时考虑部件的经济相关性和结构相关性,提出多部件系统的机会成组维修决策优化模型;考虑长期计划不能实时更新维修计划所带来的缺陷,采用滚动计划方法,提出自适应的动态维修模型,将长期计划与短期计划相结合,能够根据新信息实时地更新维修计划。此外,针对成组维修过程中部件数量n较大造成的NP难问题,应用遗传算法对各部件进行动态分组,根据得到的最优化维修结构分组进行维修不仅降低系统的维修费用、减少了维修所用时间,还能够很好地解决NP难问题。案例表明,同时考虑经济、结构相关性,将得到更优的维修策略,因此本文提出的方法值得在工程中应用。

参考文献：

[1] THOMAS L. A survey of maintenance and replacement models for maintainability and reliability of multi-item system[J]. Reliability Engineering, 1986, 16(4): 297- 309.

[2] BERG M. Optimal replacement policies for two-unit machines with increasing running costs[J]. Stochastic Processes and Their Applications, 1976, 4(1): 89-106.

[3] 杨元, 黎放, 侯重远, 等. 基于相关性的多部件系统机会成组维修优化[J]. 计算机集成制造系统, 2012, 18(4): 827-832.

YANG Y, LI F, HOU C Y, et al. Opportunistic group maintenance optimization of multi-unit system under dependence[J]. Computer Integrated Manufacturing Systems,2012,18(4):827-832.

[4] BOUVARD K, ARTUS S, BÉRENGUER C, et al. Condition-based dynamic maintenance operations planning and grouping. Application to commercial heavy vehicles[J]. Reliability Engineering and System Safety, 2011, 96(6): 601-610.

[5] SHAFIEE M, FINKELSTEIN M. A proactive group maintenance policy for continuously monitored deteriorating systems: application to offshore wind turbines[J]. Proceedings of the Institution of Mechanical Engineers Part O Journal of Risk and Reliability, 2015, 229(5): 373-384.

[6] HORENBEEK A V, PINTELON L. A dynamic predictive maintenance policy for complex multi-component systems[J]. Reliability Engineering and System Safety, 2013, 120(12): 39-50.

[7] WILDEMAN R E, DEKKER R, SMIT A. A dynamic policy for grouping maintenance activities[J]. Econometric Institute Research Papers, 1997, 99(3): 530-551.

[8] NGUYEN H S H, VAN P D, IUNG B, et al. A dynamic grouping maintenance strategy for geographically dispersed production systems[C]∥Proc.of the International Conference on Mathematical Methods in Reliability, 2017.

[9] WANG Y, PHAM H. A multi-objective optimization of imperfect preventive maintenance policy for dependent competing risk systems with hidden failure[J]. IEEE Trans.on Reliability, 2011, 60(4):770-781.

[10] NGUYEN K A, DO P, GRALL A. Condition-based maintenance for multi-component systems using importance measure and predictive information[J]. International Journal of Systems Science Operations and Logistics, 2014, 4(1): 228-245.

[11] 於世为,魏一鸣,诸克军.基于粒子群-遗传的混合优化算法[J].系统工程与电子技术,2011,8(8):265-274.

YU S W, WEI Y M, ZHU K J. Hybrid optimization algorithms based on particle swarm optimization and genetic algorithm[J]. Systems Engineering and Electronics, 2011, 8(8): 265-274.

[12] HEISSCZEDIK D. Introduction to genetic algorithms[J]. Energija, 2014, 3(1):63-65.

[13] 李积英, 党建武. 基于量子空间的蚁群算法及应用[J]. 系统工程与电子技术, 2013, 35(10): 2229-2232.

LI J Y, DANG J W. Ant colony algorithm and application based on quantum space[J]. Systems Engineering and Electronics, 2013, 35(10): 2229-2232.

[14] 苏春,陈武.基于滚动窗口方法的风力机动态机会维修优化[J].机械工程学报,2014,50(14):62-68.

SU C, CHEN W. Dynamic opportunistic maintenance optimization for wind turbine system based on rolling horizon approach[J]. Journal of Mechanical Engineering, 2014, 50(14): 62-68.

[15] 苏春,陈武.考虑部件经济相关性的风力机系统状态维修优化[J].东南大学学报(自然科学版),2016,46(5): 1007-1012.

SU C, CHEN W. Optimization of condition based maintenance for wind turbine system considering economic dependence among components[J]. Journal of Southeast University (Natural Science Edition), 2016, 46(5): 1007-1012.

[16] DO P, VU H C, BARROS A, et al. Maintenance grouping for multi-component systems with availability constraints and limited maintenance teams[J]. Reliability Engineering and System Safety, 2015, 142: 56-67.

[17] DO P, VU H C, BARROS A, et al. Opportunistic maintenance based on multi-dependent components of manufacturing system[J].CIRP Annals-Manufacturing Technology,2016, 65(1): 401-404.

[18] VAN P D, HAI C V, BARROS A, et al. Grouping maintenance strategy with availability constraint under limited repairmen[J]. IFAC Proceedings Volumes, 2012, 45(20): 486-491.

[19] HAI C V, VAN P D, BARROS A, et al. Dynamic grouping maintenance for complex structure systems with non-negligible replacement time[J]. IFAC Proceedings Volumes, 2012, 45(31): 79-84.

[20] VAN P D, BARROS A, BéRENGUER C, et al. Dynamic grouping maintenance with time limited opportunities[J]. Reliability Engineering and System Safety, 2013, 120(120): 51-59.

[21] HAI C V, DO P, BARROS A. A stationary grouping maintenance strategy using mean residual life and the birnbaum importance measure for complex structures[J]. IEEE Trans.on Reliability, 2016, 65(1): 217-234.

[22] HAI C V, DO P, BARROS A, et al. Maintenance planning and dynamic grouping for multi-component systems with positive and negative economic dependencies[J]. IMA Journal of Management Mathematics, 2015(2):145-170.

[23] HAI C V, VAN P D, BARROS A. A comparison of different maintenance grouping strategies for multi-component systems with complex structure[C]∥Proc.of the European Safety and Reliability Conference, 2015.

[24] GENG J, AZARIAN M, PECHT M. Opportunistic maintenance for multi-component systems considering structural dependence and economic dependence[J]. Systems Engineering and Electronics, 2015, 16(3): 493-501.

[25] 葛小凯, 胡剑波, 张博锋. 考虑依赖性的多部件系统状态维修优化仿真建模[J]. 航空学报, 2013, 34(8): 1854- 1863.

GE X K, HU J B, ZHANG B F. Simulation modeling for condition based maintenance optimism of multi-component systems with dependencies[J].Acta Aeronautica et Astronautica Sinica,2013,34(8): 1854-1863.

[26] 宋之杰, 常建美, 侯贵宾, 等. 多部件串联系统机会维修策略优化[J]. 机械设计与制造, 2015, 1(4): 259-262.

SONG Z J, CHANG J M, HOU G B, et al. Optimized opportunistic maintenance strategy for multi-components series system[J]. Machinery Design and Manufacture, 2015, 1(4): 259-262.

[27] LI P, SHRIVASTAVA A, MOORE J, et al. B-bit minwise hashing for large-scale learning[J]. Computer Science, 2011, 54(8): 101-109.

[28] MOGHADDAM K S, USHER J S. Sensitivity analysis and comparison of algorithms in preventive maintenance and replacement scheduling optimization models[J]. Computers and Industrial Engineering, 2011, 61(1): 64-75.

[29] DO P, VU H C, BARROS A, et al. Maintenance grouping strategy for multi-component systems with dynamic contexts[J]. Reliability Engineering and System Safety,2014,132:233-249.

[30] MEMBER S A S, NON-MEMBER B K, MEMBER M G. Optimal design of two-stage logistics network considered inventory by boltzmann random key-based GA[J]. IEEJ Trans.on Electrical and Electronic Engineering, 2010, 5(2):195-202.