多重不确定因素影响的高端装备研制任务仿真建模
张西林, 谭跃进, 杨志伟
(1. 国防科技大学系统工程学院, 湖南 长沙 410073; 2. 江苏师范大学商学院, 江苏 徐州 221116)
0 引 言
高端装备是指技术含量高、涉及学科多、资金投入大、具有高附加值、服役寿命长,一般需要跨领域、跨行业、跨区域的多个企业共同协作才能完成的一类技术装备,如航空航天装备、海洋工程装备、轨道交通装备、卫星、智能制造装备等。高端装备研制任务通常包含许多子任务,子任务之间存在串行、并行、重叠和耦合等关系,而且任务网络复杂、随机性大、影响因素多、返工迭代多。各个子任务的成功概率、完成时间、消耗成本、返工迭代次数等都存在着一定的不确定性,需要综合考虑这些因素,以便对其工期、成本、风险等进行更准确的预测、评估和控制。
计划评审技术(program evaluation and review technique,PERT)是美国研制北极星导弹时提出并发展起来的一种网络计划技术,主要用于项目的工期优化、关键路线识别、敏感性分析等。文献[1-2]利用PERT网络模型研究了项目管理和装备研制的工期估算问题。但是PERT是一个确定性的网络,而且不允许存在回路,难以对高端装备研制任务的迭代、重叠等进行描述。图示评审技术(graphical evaluation and review technique,GERT)方法可以将研制任务或项目的各个活动的参数设为随机分布,而且网络中允许存在自环和回路。文献[3-6]利用GERT网络模型从不同角度研究了复杂装备研制问题。但是GERT无法描述高端装备研制任务中的子任务重叠和学习曲线。
文献[7]将设计结构矩阵(design structure matrix,DSM)应用到复杂系统分析与管理,DSM在产品的流程优化、协同设计、风险分析等领域得到了广泛的应用[8-10]。DSM用方阵表示项目中活动之间的串行、并行、耦合和重叠等关系,能够有效解决流程分析建模、仿真与优化等问题。文献[9-10]结合不同实例分别研究了DSM的应用,指出研究DSM需要结合图论、网络分析、复杂网络等理论。文献[11]首次构建了基于DSM的产品研发流程架构仿真模型,奠定了基于DSM的研发任务仿真的基础,该模型可以分析不同流程下的进度、风险,但是未考虑资源约束。文献[12-14]通过模型分析了不同项目属性对重叠策略的影响,研究了如何确定产品开发过程中的最优重叠策略。文献[15]基于演化DSM和灵敏度DSM模型衡量重叠活动之间的交互强度。文献[16]在分析上下游活动依赖性的基础上,提出了不同重叠策略下量化产品设计演化过程的评估模型。高端装备研制过程中不可避免地会涉及到迭代过程,迭代具有积极的作用,但同时会增加研制任务的工期和成本[17-18]。当产品研制过程中允许活动返工时,产品研发工期和方差难以估计,文献[19]提出了一种研发工期和方差的估计和分析方法。文献[20]研究了结构复杂度对成本和工期的影响。文献[21-22]综合考虑返工的不确定性、返工风险等因素,采用遗传算法优化DSM。文献[23]考虑了复杂产品研发过程中活动的返工迭代、随机重叠、学习效应等多种不确定关系,建立了其仿真模型。文献[24]构造了一种基于装配特征对的装配建模与仿真集成框架。文献[25]在DSM分析的基础上,基于仿真方法评估产品架构对可演化性的影响。文献[26]综合利用DSM和网络分析方法研究了项目实施过程中任务之间的交互。文献[27]构建了能够反映产品研发过程变化的DSM网络,并提出了基于多层次建模与仿真的产品开发流程管理方法。文献[28]开发了一个离散事件仿真模型,用来分析产品设计过程中返工迭代和变更传播的影响。文献[29]在资源受限条件下,考虑节点之间的多种关系,实现了基于DSM的项目网络仿真。文献[30]考虑返工和学习效应等因素,基于离散事件仿真估计资源受限研发项目的工期。
当前文献在进行研制任务仿真时,主要考虑了其子任务的顺序、并行、重叠、返工迭代等关系,没有考虑子任务的自环和失败。在高端装备研制任务中,很多子任务都需要高新技术突破,完成时间、能否成功等都存在一定的不确定性,需要进一步考虑其子任务的自环和失败。本文在当前研究的基础上,考虑了子任务的自环、失败等因素,对高端装备研制任务进行仿真建模,使得仿真模型能够更真实地反映研制任务的实际过程。
1 高端装备研制任务仿真问题及子任务关系描述
1.1 问题描述
一般来说,高端装备研制任务可参考的历史数据、信息较少,没有类似的成功案例可供借鉴,其研制过程的不确定性更大。由于受到多种因素的影响,各个子任务完工所需的工期和成本会在一定范围内波动。某子任务完工引发的后续子任务及其执行方式是不确定的,例如,某子任务完工可能会引发自身返工或其他若干子任务的返工,也可能引发其紧后子任务的执行,而且其后续子任务可能是重叠或非重叠执行。各个子任务会存在一定的随机失败风险。在整个研制任务执行过程中,由于资源是有限的,子任务之间可能会存在资源冲突。为了实现整个研制任务的工期最短、成本最小、失败率最低等目标,需要对整个研制任务过程进行分析、优化,由于问题的复杂性高和众多的不确定性,难以用数学模型求解分析。因此,本文用一定的分布或概率描述各个子任务工期、成本及子任务之间关系的不确定性,采用离散事件仿真建模的方法对研制任务进行仿真和优化。通过仿真,能够更直观地表示研制任务执行过程中子任务的工期和成本的不确定性、子任务之间的各种关系以及执行过程中的返工迭代、重叠、失败、学习效应等,从而能够有效把握整个研制任务的工期、成本等,并可以在此基础上对各影响因素进行深入分析。
1.2 DSM、返工、重叠及学习曲线的量化表示
1.2.1 DSM的量化表示
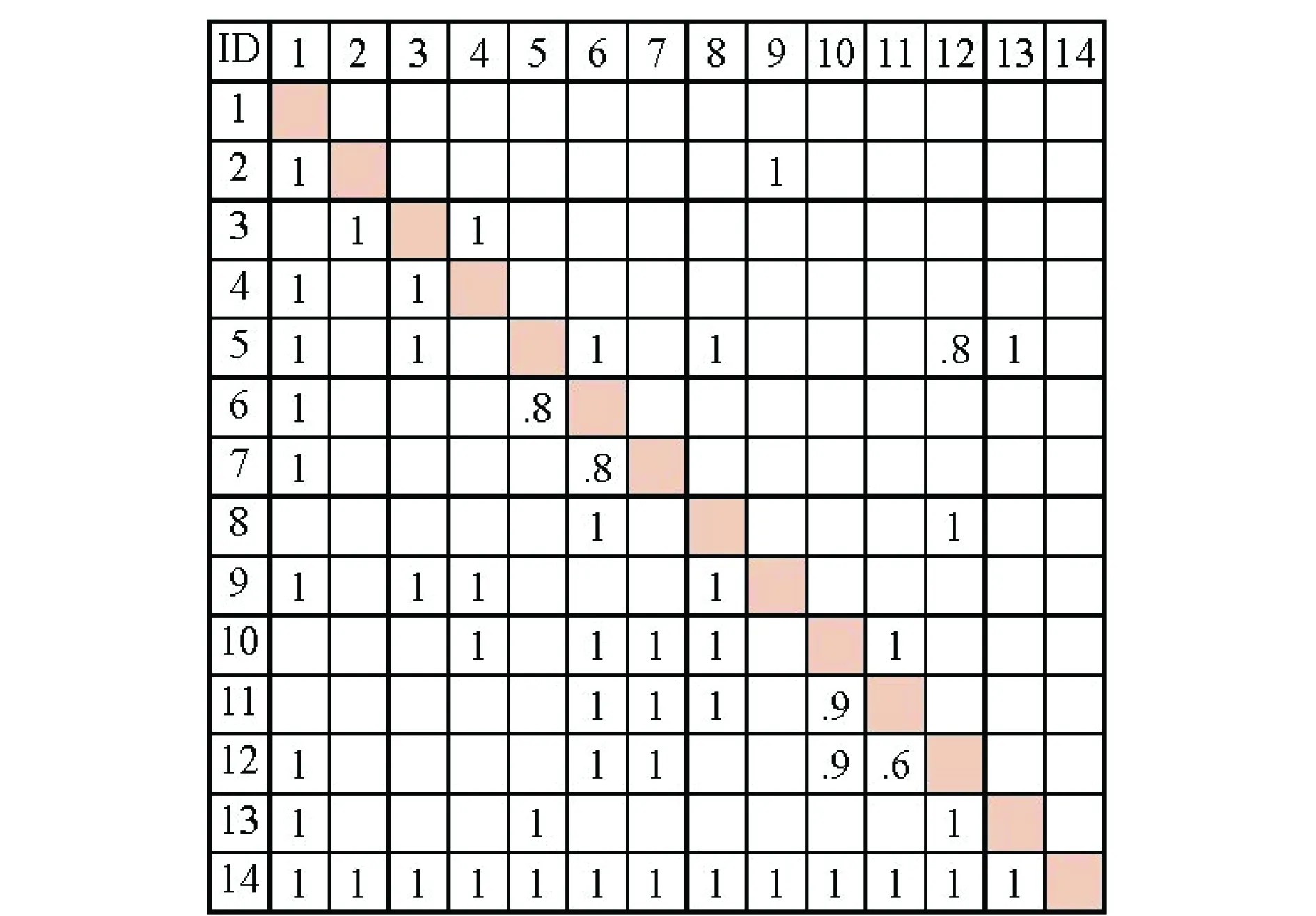
DSM的元素表示该元素对应的列任务向对应的行任务输出或者支持信息。给定n个子任务Ti(i=1,2,3,…,n)构成的研制任务过程,则DSM中各行各列对应的元素表示子任务与子任务之间的关系,矩阵中的元素Aij表示子任务Tj输出信息给子任务Ti。DSM各元素的取值定义为:DSMij=0表示子任务i与子任务j之间不存在紧前紧后关系;DSMij=1表示子任务i是子任务j的紧后任务;DSMij=p,p∈(0,1)表示子任务i与子任务j重叠执行的概率是p。
1.2.2 返工概率矩阵和返工影响矩阵
返工概率矩阵描述了返工迭代的不确定性,以一定的返工概率进行表示。其元素RPij表示子任务j引发子任务i发生返工的概率,其中i,j=1,2,3,…,n。某子任务每完成一次返工迭代,其存在错误的概率降低、产生的新信息减少,再次发生返工的概率也会随之降低。一般来说,两个子任务之间的关系越复杂,返工子任务越难以按照返工要求完成,再次返工的概率也就越大。因此,其返工概率降低系数就越大;反之,其返工概率降低系数就越小。第k次由子任务j引发子任务i发生返工的概率可表示为
(1)
式中,RPij(0)为子任务j引发子任务i返工的初始返工概率;RPLij为子任务j引发子任务i返工的概率降低系数。
返工影响矩阵表示当发生返工时,对返工子任务的影响程度。其元素RIij表示子任务j引发子任务i发生返工时,子任务i返工的工作量占其原工作量的比例,其中i,j=1,2,3,…,n。
1.2.3 学习曲线
学习曲线表示同一子任务每重复执行一次,完工所需工作量的减小程度。学习曲线的大小与子任务的复杂性有关,一般来说,子任务的复杂性越高,熟练该子任务的速度越慢,重复执行时所需的工作量越大,其学习曲线值就越大;反之,其学习曲线值就越小。LCi表示子任务i每次返工所需的工作量占其上次完工所需工作量的比例,其中i,j=1,2,3,…,n。子任务i第k次返工所需的工期和成本分别可表示为
(2)
(3)
式中,Di、Ci分别为子任务i的工期、成本。
由于每次返工需要子任务之间的信息交流、作业准备等活动,所需的工作量不能无限小,假设某子任务返工所需的工作量降低到一定程度后,以后每次返工所需工作量是固定的。
1.2.4 重叠比例矩阵和重叠影响矩阵
子任务重叠是把紧后子任务提前开始与紧前子任务进行部分并行执行,因此子任务重叠条件判断时,只有重叠概率以及资源约束两个条件都满足,才能重叠执行,而且紧前子任务开始执行之前紧后子任务不能开始执行。
重叠比例矩阵表示子任务发生重叠时允许的重叠程度。ORij表示当子任务i与子任务j发生重叠时,允许的重叠时间与子任务i工期的比,其中i,j=1,2,3,…,n。子任务i与子任务j的重叠量可表示为
OAij=min(Di×ORij,Dj)
(4)
重叠影响矩阵表示由于重叠执行引发的重叠返工程度。OIij表示当子任务i与子任务j发生重叠时,需要的重叠返工量与重叠量的比,其中i,j=1,2,3,…,n。子任务i与子任务j的重叠返工量RWij=OAij×OIij,相应的子任务i的实际工期和实际成本分别为
ADi=Di+RWij
(5)
(6)
1.3 子任务自环的量化表示
自环是子任务自身的返工。当某子任务完工后,进行验收,确定子任务是否达到要求,如果达到要求,继续进行后续子任务;如果没有达到要求,需要进行自身的返工。自环的发生具有随机性,发生自环的概率和返工影响分别在返工概率矩阵和返工影响矩阵的对角线位置进行表示。
在返工概率矩阵中,对角线元素RPii表示该元素发生自环的概率,其中:0≤RPii<1。RPii取0,表示不会发生自环;RPii取(0,1)之间的数值,表示以一定的概率RPii发生自环。在返工影响矩阵中,对角线元素RIii表示该元素发生自环时,所引起的子任务i的额外工作量的消耗量占该子任务初始工作量的比例,其中0≤RIii<1。在RPii=0的对应矩阵位置,RIii取0,表示不会发生自环;在0 高端装备研制任务的很多子任务需要高新技术突破,不能确保子任务一定能够成功完成,因此,子任务会存在着失败的可能。子任务失败往往会给整个研制任务带来毁灭性的风险,因此,在仿真过程中,需要考虑子任务失败。本文假设如果某个子任务失败,后续子任务无法继续进行,造成整个研制任务的失败,本次仿真以“任务失败”的形式结束。子任务每执行一次,会取得一定的技术突破,进行该子任务返工时,其失败概率降低,因此子任务的失败概率会随着该子任务返工次数的增加而降低。一般来说,子任务的复杂性越高,在重复执行时其失败概率的降低程度越小,其失败率降低系数越大;反之,其失败率降低系数越小。子任务i第k次执行时,其失败的概率可以表示为 (7) 式中,FPi(0)为子任务i的初始失败率;FPLi为子任务i的失败率降低系数。 在高端装备研制任务执行过程中,当多个子任务并行执行时,可能会存在资源冲突,需要进行资源占用的优先级排序。在仿真模型中,假设存在一定数量的可循环使用资源(例如人员、机器设备等),子任务执行过程中会占用一定数量的资源,子任务完工时,释放其占用的资源。 由于资源的限制,子任务之间可能会存在资源的竞争,为了缩短研制任务工期和降低研制任务成本,需要按照一定的规则进行资源占用的优先级排序。本文在传统方法的基础上提出了“改进的加权资源利用率与优先关系”(improved weighted resource utilization ration and precedence,IWRURP),同时考虑子任务的紧后子任务数量、可能引发返工子任务的数量、资源占用量、工期、是否属于返工等因素。一般来说,某子任务的紧后子任务数量和可能引发返工的子任务的数量越多,需要其信息的子任务数量就越多,该子任务需要优先执行。某子任务的工期越长,成为关键子任务的可能性越大,为了缩短总工期,其所需的资源需要优先满足。当返工子任务与首次执行子任务产生资源冲突时,首次执行子任务通常为当前完工子任务的紧后子任务,如果先执行紧后子任务,返工子任务的完工可能会引起紧后子任务的再次返工,因此返工子任务的优先级应高于首次执行的子任务。IWRURP的计算公式为 (8) 式中,ωi(0<ωi<1,i=1,2,3)为各因素的权重,且ω1+ω2+ω3=1;j为子任务的编号;Nj为子任务j的紧后子任务数与可能引发的返工子任务数之和;rj为子任务j的资源需求量;R为资源总量;L1、L2为优先级因子。 基于上述模型和分析过程,采用DSM对高端装备研制任务网络进行描述,采用离散事件仿真模型进行仿真,使用Matlab编程实现。模型输入信息为子任务工期、成本、所需资源、DSM等。某一时点上的子任务完工触发状态的转变,状态包括各子任务完工、正在执行、排队等待等。研制任务仿真的关键变量如表1所示,单次仿真运行流程图如图1所示。 表1 仿真过程中的关键变量 图1 单次仿真运行流程图Fig.1 Flow chart of a single run simulation 每次仿真运行,可以得到相应的工期T和成本C,为了得到稳定的时间和成本分布,需要多次运行仿真。仿真不断运行,直到m次运行与m-b次运行的统计量的差距稳定到一定精度α,可认为仿真输出结果稳定。仿真运行稳定时,工期T需要满足如下表达式: (9) (10) 对于成本C,采用同样的方法求出其输出结果稳定时相应的运行次数。实际仿真次数取工期T和成本C仿真输出结果稳定时的运行次数的最大值,即m=max(nT,nC)。 以某无人机研制任务为例进行算例分析,该研制任务包括14项子任务,各子任务的工期、成本、所需资源、学习曲线及失败概率数据如表2所示。假设各子任务的工期和成本均服从三角分布,用Tria(Do,Dm,Dp)描述各子任务工期的分布,其中Do为最乐观工期,Dm为最可能工期,Dp为最悲观工期;用Tria(Co,Cm,Cp)描述各子任务成本的分布,其中C0为最乐观成本,Cm为最可能成本,Cp为最悲观成本。在每次仿真运行时,用蒙特卡罗方法分别抽取各子任务的工期和成本。该无人机的研制任务的DSM如图2所示,返工概率及返工影响矩阵如图3所示,重叠比例及重叠影响矩阵如图4所示。 文献[11]中为任务可中断的仿真模型。任务不可中断是指某子任务开始执行,必须一直执行到该子任务完工,中间不允许中断;任务可中断是指某子任务开始执行后,如果有必要,在执行过程中可以中断一段时间,然后再继续执行。有些情况下,为了降低研制成本和返工次数,任务可中断是有必要的,例如图5中:子任务T3是子任务T4和T5的紧前子任务,子任务T3完工后,子任务T4和T5并行执行,子任务T5的工期大于子任务T4的工期,子任务T4完工引发子任务T3返工。这时,为了避免子任务T3完工时引发子任务T5返工,子任务T5可以暂时中断执行,等子任务T3完工后再继续执行。任务可中断相对于任务不可中断,可以降低成本、减少返工次数,但是任务可中断会减少子任务的并行执行,从而导致整个研制任务工期增大。 表2 研制任务的部分输入数据 图2 研制任务的DSMFig.2 DSM of the development tasks 图3 返工概率及返工影响矩阵Fig.3 Rework probability and rework impact matrix 图4 重叠比例及重叠影响矩阵Fig.4 Overlap rate and overlap impact matrix 考虑自环和失败,在子任务可中断条件下,研制任务仿真模型的某次运行过程的甘特图如图5所示。图中子任务T2、T8、T13在发生了自环;子任务T3、T4、T5等发生了返工,例如子任务T12完工引发了T8返工,T8返工引发了T10和T11返工,T10返工又引发了T11和T12返工;子任务T5发生了中断执行;T6与T5、T11与T10、T12与T10重叠执行。 经过多次仿真运行测试,仿真运行5 000次,相对精度α可达到0.000 1。为便于与文献中的仿真模型进行比较,本文首先使用了文献中的数据进行仿真,仿真结果与具有代表性的文献[11,23]的仿真结果比较如表3所示,“本文(不可中断)”是指使用本文构建的不可中断仿真模型;“本 文(可中断)”是指使用本文构建的可中断仿真模型;“数据1”是文献中的数据(不考虑子任务发生自环和失败);“数据2”是考虑子任务发生自环和失败的数据。使用本文构建的仿真模型,分别使用“数据1”和“数据2”仿真输出的子任务执行次数统计如表4所示。 图5 某次研制任务仿真运行的甘特图Fig.5 Gantt chart for the simulation of a development task 数据模型工期/天均值标准差成本/千美元均值标准差数据1文献[11]1381463763文献[23]13118.5920451本文(不可中断)135.17.8660.850.4本文(可中断)136.18.0658.748.5数据2本文(不可中断)144.310.0697.260.3本文(可中断)145.510.4695.058.7 表4 仿真输出的各子任务平均执行次数 本文仿真模型允许子任务重叠,而文献[11]没有考虑子任务重叠,通过允许子任务重叠可以缩短整个研制任务工期,因此本文仿真得到工期均值小于文献[11]的工期均值;但是子任务重叠会引发重叠返工,相应会增加子任务的完成时间和成本,因此本文仿真得到的成本比文献[11]的成本高。文献[23]对返工进行了限制,规定当返工改进程度小于一定值时,则不再进行返工,而本文规定只要引发返工就一定执行,因此本文使用“数据1”时仿真得到的工期均值大于文献[23]的工期均值。本文在仿真模型中定义了更多的运行规则,因而本文仿真输出数据的标准差小于文献中的标准差。仿真输出结果比较表明,本文的仿真模型能够真实反映研制任务的运行情况。 高端装备的研制成功具有重大意义,一般来说研制成功越早,越可能带来重大价值。由表3中的仿真数据可知,任务可中断虽然可以降低成本,但降低幅度很小,而且会增加工期,因此,对于高端装备研制任务来说,更适用于采用任务不可中断模式。以下使用任务不可中断、“数据2”的仿真输出数据进行分析: (1) 自环对研制任务的影响 对仿真输出的研制任务成功时的数据进行分析,由于不包括研制任务失败时的数据,相当于消除了失败因素的影响,单独考虑自环因素。研制任务成功时工期均值为144.3天、成本均值为697.3千美元,分别比不考虑子任务自环和失败时的均值增加了6.8%和5.5%,子任务总的执行次数由21.23次增加到26.87次,增加了26.6%。数据分析表明,考虑子任务自环时,研制任务工期、成本及返工次数均比不考虑自环时有所增加。 (2) 子任务失败对研制任务的影响 由仿真输出数据可知,研制任务失败次数为490次,失败率为9.8%,失败时消耗的工期均值为49.9天、费用均值为215.5千美元。如果把研制任务失败消耗的时间和费用分摊到研制任务成功的工期和成本,研制任务工期均值为149.8天、成本均值为720.6千美元,比不考虑子任务返工和失败时分别增加了10.9%和9.0%,比单独考虑自环时分别增加了3.8%和3.4%。考虑子任务失败时,虽然每个子任务失败的概率非常小,但是整个研制任务的失败风险已经比较高;如果对研制任务失败时消耗的时间和成本进行分摊,会使研制任务的平均工期和成本均有较大程度的增加。 (3) 风险分析 风险的种类很多,这里讨论任务失败、超期、超支等风险。文献[11]计划工期和成本分别为130天和630千美元,本文考虑了自环,因此需要更长的工期和更多的成本,假设计划工期和计划成本分别为145天和700千美元。根据仿真结果,研制任务成功时工期、费用的频次直方图和累积曲线分别如图6、图7所示。研制任务成功时,实际工期超过计划工期的概率为43.7%,实际成本超过计划成本的概率为42.2%,实际工期和实际成本均未超过计划要求的概率仅为41.4%。虽然单个子任务的失败风险很低甚至无失败风险,但是仿真结果表明的整个研制任务成功的概率仅为90.2%,研制任务成功且在计划工期和成本内完成的概率仅为37.3%,研制任务成功但会发生超期、超支的概率为52.9%。因此,考虑自环和失败的情况下,高端装备研制任务具有更高的风险。 图6 工期的频次直方图和累积曲线Fig.6 Frequency histogram and cumulative curve of the duration 图7 成本的频次直方图和累积曲线Fig.7 Frequency histogram and cumulative curve of the cost (4) 任务复杂性对研制任务的影响 高端装备研制任务的复杂性与整个任务网络的拓扑结构、子任务的复杂性、子任务之间关系的复杂性等因素有关。把子任务(子任务之间关系)的复杂性水平划分为极度复杂(完全不可知)、高度复杂、中度复杂、轻度复杂、简单化(完全确定)等五个等级,不同的复杂性水平对应不同的失败率降低系数、学习曲线、返工概率降低系数等仿真参数。为了明显体现复杂性对研制任务的影响效果,我们假定每次仿真时所有子任务的复杂性水平相同。根据子任务的复杂性水平、子任务之间关系的复杂性水平,分别给失败率降低系数、学习曲线、返工概率降低系数等参数赋予[0,1]之间的数值。 根据仿真数据绘制任务复杂性对研制任务影响图如图8所示。 图8 复杂性对研制任务的影响Fig.8 Influence of complexity on development tasks X轴表示子任务的复杂性水平,Y轴表示子任务之间关系的复杂性水平,Z轴分别表示研制任务的工期、成本、失败率等。可见,随着子任务复杂性水平的增高,整个研制任务的工期、成本均会增大,研制任务的失败率也会增大。随着子任务之间关系复杂性水平的增高,整个研制任务工期、成本均会增大,失败率也会有一定程度的增大,但相比子任务复杂性水平影响下失败率的增大幅度较小。同时,当子任务的复杂性水平和子任务之间关系的复杂性水平增高时,整个研制任务工期、成本的不确定性程度变大,工期、成本的方差均会增大。 高端装备研制任务中,子任务自环、返工迭代、重叠执行、失败以及资源冲突等因素都会对研制任务的工期、成本等产生影响。本文构建了考虑多重不确定影响因素的高端装备研制任务仿真模型,假定子任务自环、返工迭代、重叠执行、失败等均以随机概率发生,并考虑了学习效应,更能有效反应高端装备研制任务的真实运行情况。在此基础上,根据算例仿真输出数据对该研制任务的工期、成本、风险、复杂性影响等进行了分析。本文提出的仿真模型可用于估计工期、成本、返工次数、失败率、各子任务花费的时间和成本、复杂性对研制任务的影响、资源对研制任务的影响等信息,从而能够帮助高端装备研制任务管理者更好地预测、评估和控制研制任务过程。 参考文献: [1] HAHN E D. Mixture densities for project management activity times: a robust approach to PERT[J]. European Journal of Operational Research, 2008, 188(2): 450-459. [2] 王涛, 蔡建峰. 航空复杂产品项目活动时间混合分布估算模型的改进[J]. 运筹与管理, 2012, 21(4): 214-219. WANG T, CAI J F. Improved mixture densities for the activity time estimation in aviation complex product project[J]. Operations Research and Management Science,2012,21(4):214-219. [3] WU Y, PAN X, KANG R, et al. Multi-parameters uncertainty analysis of logistic support process based on GERT[J]. Journal of Systems Engineering and Electronics, 2014, 25(6): 1011-1019. [4] NELSON R G, AZARON A, AREF S. The use of a GERT based method to model concurrent product development processes[J]. European Journal of Operational Research,2016,250(2):566-578. [5] 刘红旗, 方志耕, 陶良彦. 复杂装备研制项目进度规划GERT网络“反问题”模型[J]. 系统工程与电子技术, 2015, 37(12): 2758-2763. LIU H Q, FANG Z G, TAO Y L. Complex equipment development project planning GERT network “inverse problem” model[J]. Systems Engineering and Electronics, 2015, 37(12): 2758-2763. [6] 陶良彦,刘思峰,方志耕,等.基于多层次GERT的复杂产品研制进度规划“超冲突均衡”博弈模型[J].控制与决策,2014,29(11): 2002-2010. TAO Y L, LIU S F, FANG Z G, et al. “Super-conflict equalization” game model for complex product development scheduling based on multi-level GERT[J].Control and Decision,2014,29(11):2002-2010. [7] STEWARD D V. The design structure system: a method for managing the design of complex systems[J]. IEEE Trans.on Engineering Management, 1981,28(3): 71-74. [8] FANG C, MARLE F. Dealing with project complexity by matrix-based propagation modelling for project risk analysis[J]. Journal of Engineering Design, 2013, 24(4): 239-256. [9] BROWNING T R. Applying the design structure matrix to system decomposition and integration problems: a review and new directions[J]. IEEE Trans.on Engineering Management, 2001, 48(3): 292-306. [10] BROWNING T R. Design structure matrix extensions and innovations: a survey and new opportunities[J]. IEEE Trans.on Engineering Management, 2016, 63(1): 27-52. [11] BROWNING T R, EPPINGER S D. Modeling impacts of process architecture on cost and schedule risk in product development[J]. IEEE Trans.on Engineering Management, 2002, 49(4): 428-443. [12] LIN J, CHAI K H, WONG Y S, et al. A dynamic model for managing overlapped iterative product development[J]. European Journal of Operational Research, 2008, 185(1): 378-392. [13] LIN J, CHAI K H, BROMBACHER A C, et al. Optimal overlapping and functional interaction in product development[J]. European Journal of Operational Research,2009,196(3):1158-1169. [14] LIN J, QIAN Y, CUI W, et al. Overlapping and communication policies in product development[J]. European Journal of Operational Research, 2010, 201(3): 737-750. [15] YANG Q, YAO T, LU T, et al. An overlapping-based design structure matrix for measuring interaction strength and clustering analysis in product development project[J]. IEEE Trans.on Engineering Management, 2014, 61(1): 159-170. [16] ZHANG D, BHUIYAN N. A study of the evolution of uncertainty in product development as a basis for overlapping[J]. IEEE Trans.on Engineering Management, 2015, 62(1): 39-50. [17] WYNN D C, ECKERT C M. Perspectives on iteration in design and development[J]. Research in Engineering Design, 2017, 28(2): 153-184. [18] MEIER C, BROWNING T R, YASSINE A A, et al. The cost of speed: work policies for crashing and overlapping in product development projects[J]. IEEE Trans.on Engineering Management, 2015, 62(2): 237-255. [19] NASR W, YASSINE A, KASM O A. An analytical approach to estimate the expected duration and variance for iterative product development projects[J]. Research in Engineering Design, 2016, 27(1): 55-71. [20] REBENTISCH E, SCHUH G, RIESENER M, et al. Assessment of changes in technical systems and their effects on cost and duration based on structural complexity[J]. Procedia Cirp, 2016, 55: 35-40. [21] 杨青, 吕杰峰. 基于DSM返工风险评价矩阵的项目优化与仿真[J]. 系统工程理论与实践, 2010, 30(9): 1665-1671. YANG Q, LÜ J F. Project optimization and simulation based on DSM rework risk evaluation matrix[J]. Systems Engineering-Theory & Practice, 2010, 30(9): 1665-1671. [22] COOK I, COATES G. Optimising the time-based design structure matrix using a divide and hybridise algorithm[J]. Journal of Engineering Design, 2016, 27(4/6): 306-332. [23] 李洪波,徐哲.考虑活动随机重叠和资源冲突的复杂产品开发流程仿真建模[J].系统工程与电子技术,2012,34(7): 1412-1418. LI H B, XU Z. Simulation modeling of complex product deve-lopment process considering stochastic activities overlap and resource conflict[J]. Systems Engineering and Electronics, 2012, 34(7): 1412-1418. [24] ZHANG J, XU Z, LI Y, et al. Framework for the integration of assembly modeling and simulation based on assembly feature pair[J]. International Journal of Advanced Manufacturing Technology, 2015, 78(5/8): 765-780. [25] LUO J. A simulation-based method to evaluate the impact of product architecture on product evolvability[J]. Research in Engineering Design, 2015, 26(4): 355-371. [26] COLLINS S T, YASSINE A A, BORGATTI S P. Evaluating product development systems using network analysis[J]. Systems Engineering, 2009, 12(1): 55-68. [27] KARNIEL A, REICH Y. Multi-level modelling and simulation of new product development processes[J]. Journal of Engineering Design, 2013, 24(3): 185-210. [28] MAIER J F, WYNN D C, BIEDERMANN W, et al. Simulating progressive iteration, rework and change propagation to prioritise design tasks[J]. Research in Engineering Design, 2014, 25(4): 283-307. [29] CHO S H, EPPINGER S D. A simulation-based process model for managing complex design projects[J]. IEEE Trans.on Engineering Management, 2005, 52(3): 316-328. [30] ABDELSALAM H M, RASMY M H, MOHAMED H G. A simulation-based time reduction approach for resource constrained design structure matrix[J]. International Journal of Modeling & Optimization, 2014, 4(1): 51-55.1.4 子任务失败的量化表示
2 返工优先的资源冲突处理规则
3 仿真算法设计

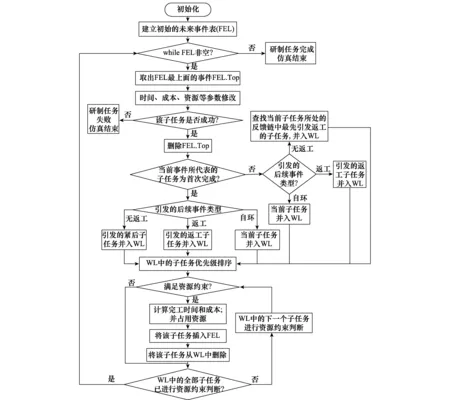
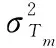
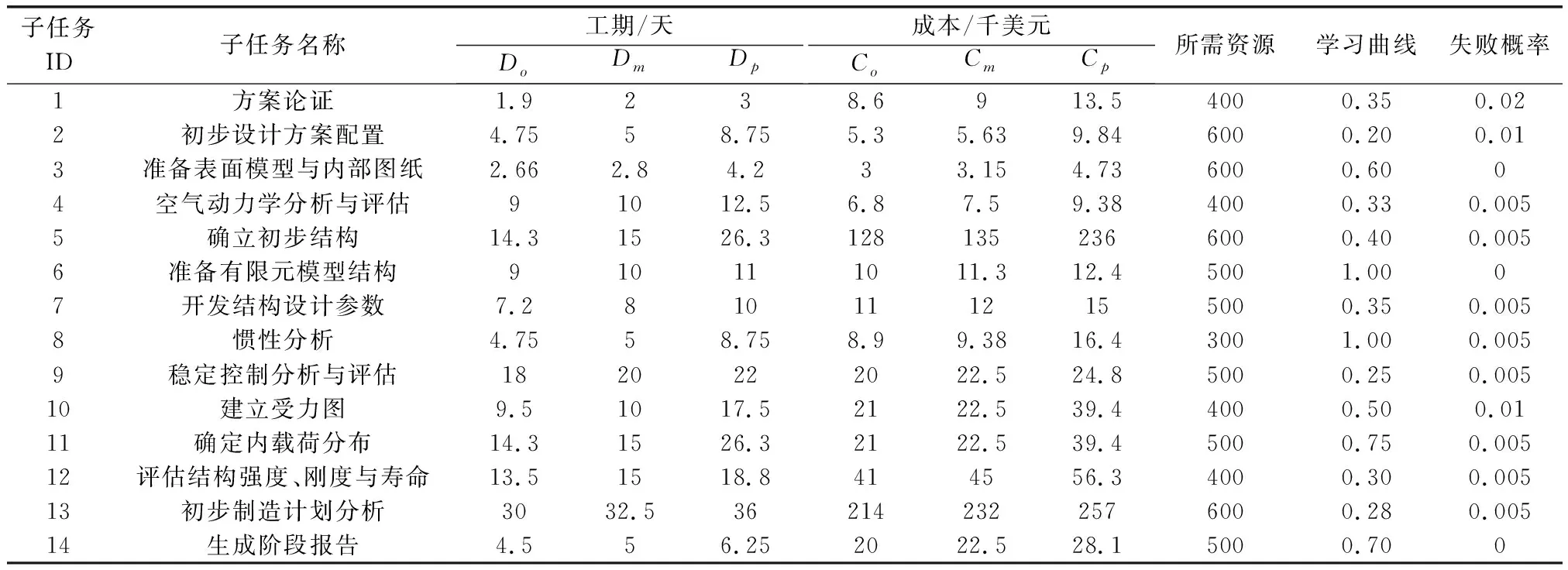
4 算例研究
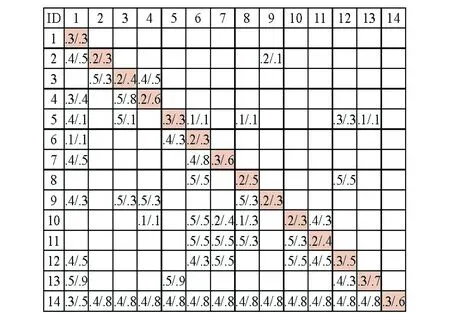
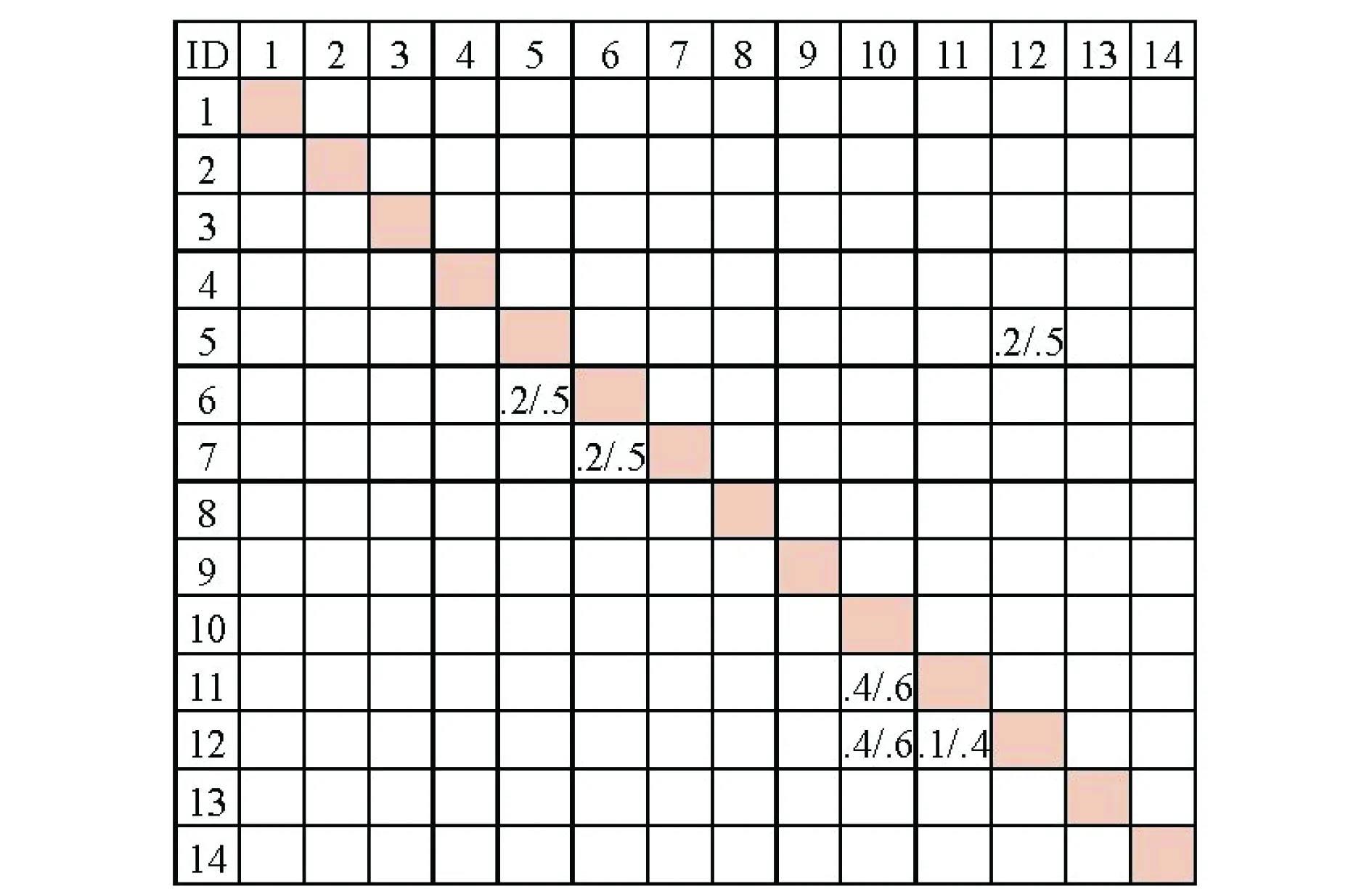
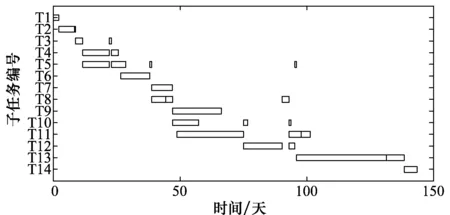
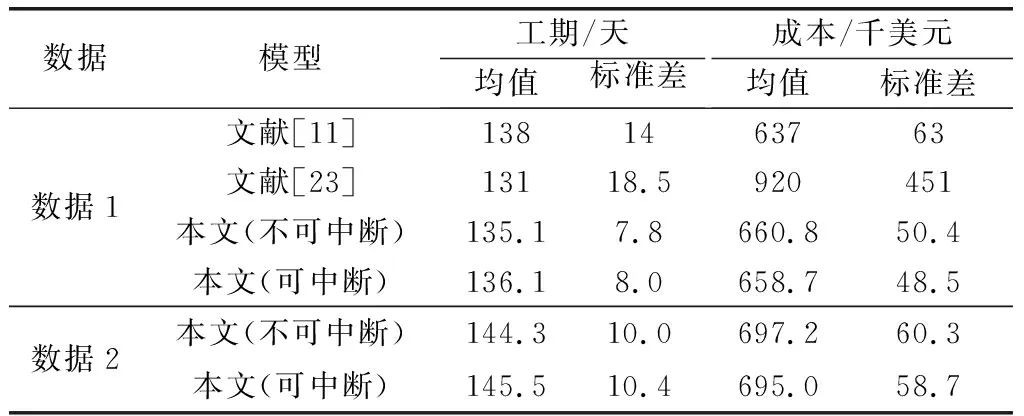

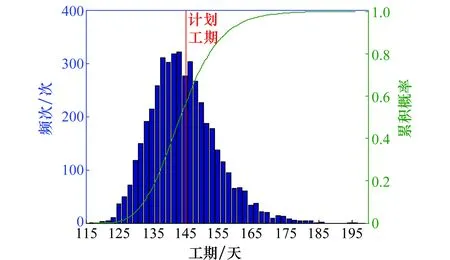
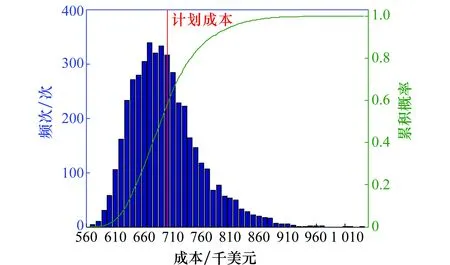
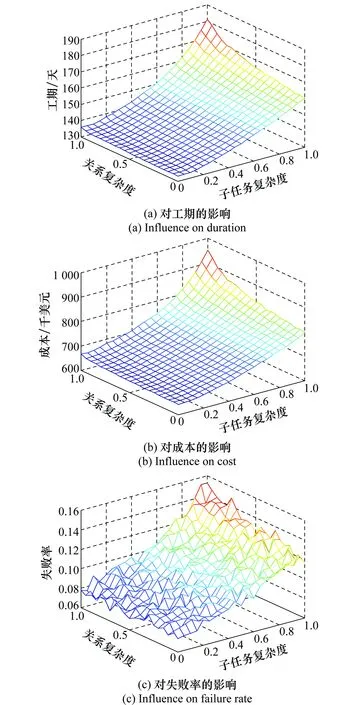
5 结 论

