面向突防的多约束滑翔弹道优化设计

许强强, 葛健全, 杨 涛, 陶 烨, 黄 浩

(国防科技大学航天科学与工程学院, 湖南 长沙 410073)

0 引 言

在导弹突防过程中,隐身性能发挥着重要的作用,提高隐身技术一方面可从降低自身特征信号入手,另一方面则是通过弹道规划,降低雷达探测概率。因此,采取快速通过雷达探测区、反导防御区的战术规避技术,能够有效增加高超声速助推滑翔飞行器打击目标的突然性,提高突防性能。如何在弹道设计过程中描述此类路径(本文定义为辐射型禁飞区)约束则是首要解决问题。

目前对于路径约束的研究主要侧重于禁飞区建模方面,Timothy等[1]在平面地球的模型下,建立了无限长圆柱的禁飞区模型并设计了最优轨迹;在此基础上,相关学者对该禁飞区模型下的轨迹优化[2-5]、制导[6-9]等方面内容进行了研究。陈小庆等[10]则是基于球面模型的基础上利用球面三角形原理建立了无限长圆柱的禁飞区模型;谢愈等[11]建立了半椭球的禁飞区模型,张梦樱[12]基于立体几何原理在地心系下建立了禁飞区的半椭球空间几何数学模型。

这样的模型一方面难以反映飞行器可以进入但存在一定的暴露危险的特征;另一方面绝对的边界锁定使得求解更加困难,甚至无法得到最优解。同时,在实际作战过程中,雷达探测区域半径较大,采用上述模型将对飞行器横侧向机动能力提出严峻挑战。

为更准确方便地处理辐射型禁飞区约束,本文根据将禁飞区内威胁量化的思想[13],将禁飞区约束转化为与威胁系数积分相关的目标函数,并通过分析雷达探测模型,建立辐射型禁飞区内的威胁模型,然后得到辐射型禁飞区约束对应的最优控制问题模型。

最后考虑到实际飞行距离长、空域广、速域宽等特点,飞行器受到严峻的动压、过载、热流等过程约束的影响,飞行轨迹将被限制在较为狭窄的范围。对于此种同时含有端点约束、过程约束、路径约束等多约束下的轨迹优化问题可以归结为强非线性、多阶段、多约束的最优控制问题,其求解十分困难。伪谱法作为求解复杂最优控制问题的工具,近年来得到迅速发展。本文基于hp-自适应Radau伪谱法、借鉴逐步增加约束方法完成对此轨迹优化问题求解,得到优化的滑翔段弹道。

1 数学模型

1.1 再入动力学模型

忽略地球的自转和非球形影响,在极坐标系下建立高超声速滑翔飞行器的再入运动方程[14]:

(1)

式中,m为飞行器质量;g为重力加速度;r=R+h为地心距,r为地球半径,h为飞行器高度;λ为地理经度;φ为地理纬度;V为飞行器速度;θ为当地速度倾角;σ为速度偏角(参考方向为当地正北方向);ν为飞行器的倾侧角;L为升力;D为阻力。升力L和阻力D的表达式分别为

(2)

式中,ρ为空气密度;ρV2/2为动压头;ρ0e-β(r-r0)为指数大气模型;Cl为升力系数;Cd为阻力系数;S为飞行器特征面积。

1.2 端点约束

对于初始状态,通常为固定值;而终端约束通常是由飞行任务和末制导交接班要求所决定,若要使飞行器到达指定点,则需对位置参数:地心距、地理经度、地理纬度进行约束,即

(3)

根据作战任务要求,还需要对末端攻击速度和攻击角度进行限制,即

(4)

1.3 控制变量约束

控制变量取为飞行器的攻角α和倾侧角ν,其约束为

(5)

1.4 过程约束模型

飞行器再入过程约束通常包括:动压约束、法向过载约束、驻点热流约束。根据基本的气动力热的理论,结合相关的工程估算技术,得到过程约束模型如下:

(6)

(7)

(8)

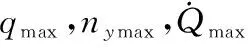
1.5 威胁模型与性能指标函数

针对辐射型禁飞区内不同的空间位置所对应的威胁不同,提出如下假设:任意位置上的威胁可以通过单位时间内该位置上的威胁系数来量化。相应的问题就转化为如何确定禁飞区内任意位置的威胁系数,即禁飞区的威胁模型。

相关研究[15]表明,雷达发现目标的概率与目标位置对应的信噪相关,假设在雷达覆盖区内,任意位置的威胁系数与该位置的信噪比成正比,即:

Rk∞S/N

(9)

式中,Rk为威胁系数;S/N为雷达的信噪比。

理想情况下雷达的信噪比为

(10)

式中,Ps是无气象干扰时的接收信号功率;N是雷达噪声功率,视为常数。

由雷达方程可以求出:

(11)

式中,Pt,G,δ,λ分别为雷达的发射机功率、天线的增益、目标的雷达截面积以及工作波长,在目标飞行器和雷达都确定的情况下都可以视为常数;Rd为理想情况下的雷达作用距离,即雷达与目标飞行器的距离。

令

则有

进一步有

其中当雷达和目标飞行器都确定的情况下,K和N均可视为常数,理想情况下信噪比与距离的关系如图1所示。

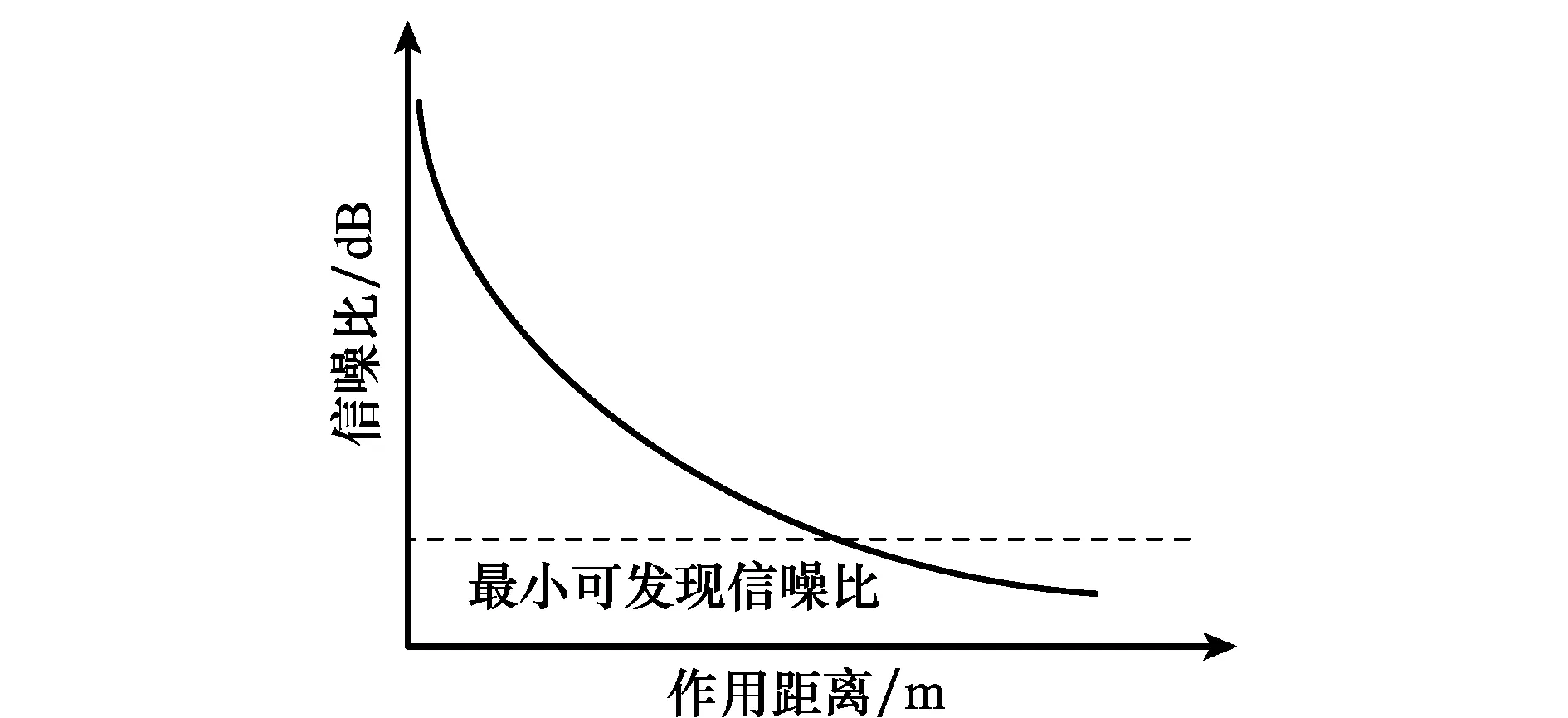
图1 理想情况下信噪比与作用距离的关系图Fig.1 Signal to noise ratio vs. distance in ideal conditions

又威胁系数Rk∞S/N,所以

(12)

式中,C为比例系数,可根据实际情况由用户确定。

为了便于计算,定义威胁系数因子:

(13)

理想情况下,在雷达和目标飞行器都确定的情况下,Cr为常数,由雷达系统确定。

得到威胁系数Rk表达式如下:

(14)

这里,为了计算的方便,假设雷达的探测距离为无穷远,当Rd很大,则Rk很小,其对积分结果的影响很小,故可以对Rk进行全弹道积分,由此得到基于威胁系数积分的弹道优化性能指标函数如下:

(15)

从该函数可以看出,全程威胁积分越小,则需飞行器与雷达的距离越远,相应地会增加飞行距离;而飞行距离的增加,使得飞行时间延长,全程威胁积分增加。因此,存在一个飞行时间和作用距离的组合使得全程威胁积分最小。显然,该性能指标函数成功地将飞行时间和绕飞距离两个指标综合到了一起,为辐射型禁飞区的处理提供了便利。

2 求解策略

2.1 hp-自适应Radau伪谱法

近年来,由于伪谱法具有收敛半径大、对初值不敏感、收敛速度快等特点,被广泛应用于飞行器轨迹优领域中,并取得了一定的研究成果[16]。hp-自适应Radau伪谱法结合了优化网格数目(h方法的计算稀疏性)和增阶(p方法的快速收敛性)两方面的优势,能够较好地处理具有多约束条件下的最优控制问题[17]。Radau伪谱法的基本原理是:将每一个网格区间上的状态变量和控制变量在众多LGR(Legendre-Gauss-Radau)点上进行离散,并将离散点作为节点,进而创建Lagrange插值多项式,以拟合近似状态变量和控制变量。通过对全局插值多项式得到的状态变量进行求导,来近似状态变量对时间的导数,从而可以将系统的动力学微分方程约束转化为代数约束,性能指标中的积分则由Radau积分进行计算。由于全局当前网格区间的终端状态为下一网格区间的初始状态,由此避免了全局Radau伪谱法中终端状态的积分过程。通过上述一系列步骤,可以将原有的最优控制问题变为非线性规划问题(nonlinear programming,NLP)。

Radau伪谱法的求解具体步骤可参考相关文献[18-19],本文不再详述。其中将Bolza型性能指标函数中的积分项用LGR积分近似,得到近似性能指标函数如下:

J=Φ(X0,t0,Xf,tf)+

(16)

式中,Φ为非积分项指标;g为积分项指标的被积分项。

对于本文,性能指标函数如式(15)所示。

2.2 逐步增加约束方法

考虑多约束条件下飞行器轨迹优化问题比较复杂,直接采用伪谱法求解难以得到优化结果。故借鉴于文献[12],采用逐步增加约束的方法,将具有较少约束问题的优化结果作为下一步的优化初值进行迭代,流程如图2所示。

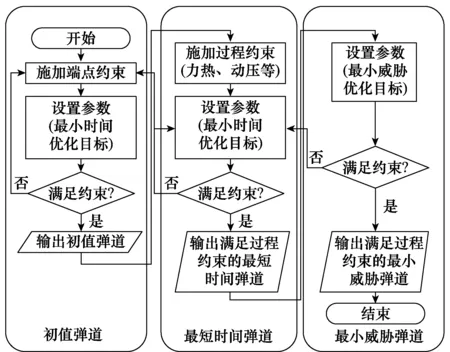
图2 逐步增加约束方法流程图Fig.2 Flow chart of adding constraints

其具体步骤为:

步骤1基于前面建立的最优控制问题的模型,添加必要的端点约束并配置好数值算法,以最短时间为优化目标,得到满足端点约束的最优弹道,验证目标可达性;

步骤2在步骤1的模型基础上添加飞行过程约束,以步骤1的优化结果作为求解初值,以最短时间为优化目标,保证在过程约束下目标可达性;

步骤3在步骤2的基础上,添加辐射型禁飞区约束,将性能指标函数改成威胁最小,以步骤2中最短时间弹道为初值,求解绕过禁飞区时的威胁最小弹道。

3 仿真结果及分析

3.1 仿真条件

取飞行器质量为1 500 kg,参考面积1 m2。严格来讲,气动系数通常与飞行高度、马赫数和攻角三者相关,可表示为三者的函数。但在高超声速条件下,飞行器的气动系数遵循马赫数无关原理[20],可以认为气动系数仅随攻角变化,本文中取飞行器的气动系数与攻角的关系为

(17)

式中,Cl,Cd分别为飞行器的升力系数和阻力系数;α为飞行器攻角。

具体仿真参数如表1所示。同时,由于Cr=1,计算过程中,为了降低计算难度、提高计算效率,本文采用无量纲化的方法,取长度的单位长度为地球半径,取质量的单位质量为飞行器质量。

表1 多约束条件设置

3.2 优化结果及分析

本文仿真选择最短时间弹道和最小威胁弹道作对比。优化目标分别为

Jtime=tf

(18)

(19)

(1) 绕飞情况对比

最短时间弹道和最小威胁弹道的结果如图3所示,实线表示的是最短时间弹道,虚线表示的是最小威胁弹道,可以很明显的看出飞行器成功绕过禁飞区中心。

图3 最短时间弹道和威胁最小弹道对比图Fig.3 Comparison diagram of minimum time trajectory and minimum threat trajectory

对时间最短弹道和威胁最小弹道的威胁系数积分,结果分别为

Jmin time=3.773 1e-18

(20)

Jmin risk=8.646 1e-22

(21)

从积分结果对比可以看到威胁最小弹道的威胁系数积分与最短时间弹道的相差10-4量级,从这一方面也说明了这种辐射型禁飞区的处理方式是正确有效的。

通过简单的理论分析可以得到,对于固定中心的辐射型禁飞区,由于威胁系数与距离的关系,若使全程的威胁积分最小,可在两个方面做出变化:一是增大飞行器与禁飞区中心的径向距离,二是考虑到时间对积分的影响,当威胁系数相对较大时,提高飞行器速度,缩短通过高威胁区域时间。

从图3(b)可以看出,飞行器比较靠近禁飞区时的经度范围为35°～45°,两条弹道对应的飞行时间范围为500～900 s。

下面将结合图中两弹道信息的对比分析上述缩小全程威胁积分的2个方面分别的体现:

①从图3(a)的平面轨迹对比中可以很明显的看出,在接近禁飞区中心时,最小威胁弹道与中心的水平距离明显增大,相对减小了威胁系数;

②从图3(c)的高度时间变化关系对比中可以看出,在500～900 s的范围内,最小威胁弹道的高度总体要比最短时间弹道的高,但是差别无水平距离明显;

③从图3(d)的速度时间变化关系对比,显然地最小威胁弹道的速度要高于最短时间弹道,对应的就是如果在覆盖区内飞过同样的距离,最小威胁弹道用时更短,威胁积分也更小。

通过上述分析,最小威胁弹道的仿真结果所体现的绕飞途径与理论分析相吻合,这也进一步验证了本文中建立的辐射型禁飞区的威胁模型和将辐射型禁飞区约束转换为与威胁积分相关的性能指标函数的处理方法的正确性。

(2) 约束满足度和可行性分析

最小威胁弹道的过程约束和控制变量随时间的变化关系如图4所示。

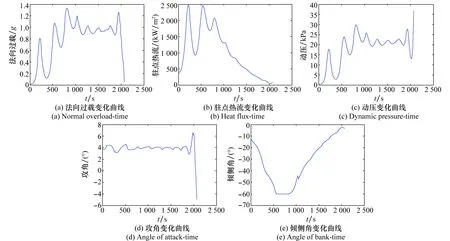
图4 最小威胁弹道的过程约束和控制变量变化曲线Fig.4 Curves of process constraints and control variables in minimum threat trajectory

关于过程约束,由图4(a)～图4(c)可知,法向过载、驻点热流和动压均满足给定的约束范围。

关于控制变量,攻角大部分时间稳定在4°附近,仅在结束时变化较大,这也是符合飞行器滑翔段保持小攻角飞行的特征;倾侧角在全程为负值,在绕飞阶段达到极值,这也符合飞行轨迹左倾且在绕飞阶段曲率较大的特征。

关于终端约束,最小威胁弹道能准确到达终点(60°E,35°N),且Hf=20 km,同时速度也满足给定的终端速度范围。

综上,最小威胁弹道能够满足所给定的过程约束,同时其优化得到的控制变量的变化在给定约束范围之间,故最小威胁弹道是可行的。

4 结 论

本文面向助推滑翔飞行器突防,对多约束条件下的滑翔段弹道进行了优化设计。针对传统路径约束建模的不足,建立了辐射型禁飞区模型。采用了逐步增加约束的方法,利用hp-自适应Radau伪谱法对滑翔段弹道进行了优化设计,成功得到了满足相关约束且使全程威胁积分最小的优化弹道,达到了快速突防的目的。并且结果弹道反映的信息与理论分析一致,也证明了本文中建立的威胁模型和针对辐射型禁飞区时处理方法的正确性,为面向突防的滑翔段弹道优化设计提供了有效的方法。

参考文献：

[1] JORRIS T R, COBB R G. Three-dimensional trajectory optimization satisfying waypoint and no-fly zone constraints[J].Journal of Guidance, Control, and Dynamics, 2009, 33(2): 551-572.

[2] WANG L, XING Q H, MAO Y F. Reentry trajectory rapid optimization for hypersonic vehicle satisfying waypoint and no-fly zone constraints[J]. Journal of Systems Engineering and Electronics, 2015, 26(6): 1277-1290.

[3] ZHAO D J, SONG Z Y. Reentry trajectory optimization with waypoint and no-fly zone constraints using multiphase convex programming[J].Acta Astronautica, 2017, 137: 60-69.

[4] MAO Y F, ZHANG D L, WANG L. Reentry trajectory optimization for hypersonic vehicle based on improved Gauss pseudospectral method[J]. Soft Computing, 2016, 21(16): 1-10.

[5] LIU X F, SHEN Z J, LU P. Entry trajectory optimization by second-order cone programming[J]. Journal of Guidance Control & Dynamics, 2015, 39(2): 1-15.

[6] LIANG Z X, LIU S Y, LI Q D, et al. Lateral entry guidance with no-fly zone constraint[J].Aerospace Science & Technology,2017,60: 39-47.

[7] ZHANG D, LIU L, WANG Y J. On-line reentry guidance algorithm with both path and no-fly zone constraints[J]. Acta Astronautica, 2015,117: 243-253.

[8] LIANG Z X, REN Z, BAI C. Lateral reentry guidance for maneuver glide vehicles with geographic constraints[C]∥Proc.of the Control Conference, 2013: 5187-5192.

[9] GUO J, WU X Z, TANG S J. Autonomous gliding entry guidance with geographic constraints[J]. Chinese Journal of Aeronautics, 2015, 28(5): 1343-1354.

[10] 陈小庆,侯中喜,刘建霞. 高超声速滑翔飞行器再入轨迹多目标多约束优化[J]. 国防科技大学学报,2009,31(6):77-83.

CHEN X Q, HOU Z X, LIU J X. Multi-objective optimization of reentry trajectory for hypersonic glide vehicle with multi-constraints[J].Journal of National University of Defense Technology, 2009, 31(6): 77-88.

[11] 谢愈, 刘鲁华, 汤国建. 多约束条件下高超声速度滑翔飞行器轨迹优化[J]. 宇航学报,2011,32(12):2499-2504.

XIE Y, LIU L H, TANG G J. Trajectory optimization for hypersonic glide vehicle with multi-constraints[J]. Journal of Astronatics, 2011, 32(12): 2499-2504.

[12] 张梦樱, 唐乾刚, 韩小军, 等. 复杂约束条件下的再入轨迹迭代求解方法[J]. 兵工学报,2015, 36(6): 1015-1023.

ZHANG M Y, TANG Q G, HAN X J, et al. Iterative method to solving re-entry trajectory optimization with complex constraints[J].Acta armamentarii, 2015, 36(6):1015-1023.

[13] VIAN J L, MOORE J R. Trajectory optimization with risk minimization for military aircraft[J]. Guidance, 1989, 12(3): 311-317.

[14] VINH N X. Optimal trajectories in atmospheric flight[M]. New York: Elsevier Scientific Publishing Company, 1981.

[15] 丁鹭飞,耿富录.雷达原理[M].西安:西安电子科技大学出版社, 2003: 128-134.

DING L F, GENG F L. Principle of radar[M].Xi’an: Xidian University Press, 2003: 128-134.

[16] 王海涛,李军营,梁立威,等.基于hp自适应Radau伪谱法的再入飞行器轨迹优化[J].科学技术与工程,2015,15(2):165-171.

WANG H T, LI J Y, LIANG L W, et al. Track optimizing for reentry vehicle based on hp- adaptive radau pseudospectural method[J]. Science Technology and Engineering,2015,15(2): 165-171.

[17] 刘鹤鸣,丁达理,黄长强,等.基于自适应伪谱法的UCAV低可探测攻击轨迹规划研究[J].系统工程与电子技术,2013,35(1): 78-84.

LIU H M, DING D L, HUANG C Q, et al. UCAV low observable attacking trajectory planning based on adaptive pseudospectral method[J].Systems Engineering and Electronics,2013,35(1):78-84.

[18] CHRISTOPHER L D, WILLIAM W H, ANIL V R. An hp-adaptive pseudospectral method for solving optimal problems[J].Optimal Control Applications and Methods,2011,32:476-502.

[19] CAMILA C F, ANIL V R. Direct trajectory optimization and costate estimation of state inequality path-constrained optimal control problems using a radau pseudospectral method[C]∥Proc.of the AIAA Guidance,Navigation,and Control Confe-rence, 2012.

[20] 雍恩米,唐国金,陈磊.基于Gauss伪谱方法的高超声速飞行器再入轨迹快速优化[J].宇航学报, 2008, 29(6): 1766-1772.

YONG E M, TANG G J, CHEN L. Rapid trajectory optimization for hypersonic reentry vehicle via gauss psedospectral method[J].Journal of Astronautics,2008,29(6):1766-1772.