多变量离散灰色幂模型构建及其优化研究

丁 松, 党耀国, 徐 宁, 王俊杰, 耿率帅

(1. 南京航空航天大学经济与管理学院, 江苏 南京 211106;2. 南京审计大学管理科学与工程学院, 江苏 南京 211815)

0 引 言

针对经济社会生活中广泛存在的多变量非线性系统建模问题,众多学者对其展开了深入研究,主要方法是采用以概率论为基础的多元统计分析技术[1],而该方法受限于大样本的原始数据(样本量大于30),而对于小样本量的经济社会问题则难以有效解决。为了解决“贫信息、少数据”多变量不确定系统的分析、建模、预测与控制问题,文献[2]提出了多变量灰色GM(1,N)预测模型。GM(1,N)模型本质上是描述一个系统行为特征变量受到N-1个影响因素作用的因子分析模型,能够对受到多因素影响的贫信息系统趋势进行预测,因此学者对其进行优化与拓展,并成功应用到交通、农业、能源、管理等多个领域。

文献[3]将驱动项视为灰常量,为解决传统模型的模拟预测问题提供了一种有效方法,并在后续研究中得到广泛应用;文献[4]研究了数乘变换对GM(1,N)模型参数的影响;针对GM(1,N)模型的时间响应函数和背景值不精确,以及建模精度不高等问题,已有学者对其参数进行了优化,取得一些有价值的成果;文献[5]利用残差修正技术和新型背景值优化方法,提出了具有全适性的GM(1,N)模型,能够适应多种特征序列建模;文献[6]发现传统GM(1,N)模型的近似时间响应式会产生难以接受的实验误差,通过引入灰色控制参数和利用卷积积分技术求解出模型的精确解,随后,提出两种改进模型[7-8],增强了新模型对多种特征序列的建模效果;文献[9]利用Simpson公式构造GM(1,N)模型的新算法,探究估计参数的新思路。在对驱动因素改善方面,文献[10]研究虚拟驱动变量对系统行为的作用效果,构建了基于虚拟驱动项的多变量离散模型;文献[11]对驱动因素变化趋势进行建模,并将其与系统行为变量建模相融合,实现对我国粮食产量趋势的直接预测;文献[12]通过引入驱动控制函数反映各因素在不同阶段对系统变量的差异化作用效果;文献[13]在驱动项中加入灰作用量和线性控制项,增强传统模型对线性序列的适应性。

另外,部分学者将GM(1,N)模型与其他模型相结合,提出了新的拓展模型,进一步丰富多变量灰色模型体系。文献[14]将单变量离散模型拓展到多变量,并与传统GM(n,h)对比分析,研究其相关性质;文献[15]构建时滞多变量离散灰色预测模型,并利用灰色扩维技术和灰色关联分析方法对时滞参数进行估计;文献[16]提出了分数阶累加模型,并在武汉市科技投入与经济增长的时滞关系研究中取得较好应用效果;文献[17]提出了多变量灰色GM(1,N)幂模型及其派生模型,提升对多变量非线性系统特征序列的建模效果。文献[18]从建模机理、参数估计和模型结构3个角度分析传统GM(1,N)存在的缺陷,并通过引入线性修正项和灰作用项到模型构建中,克服传统模型缺陷,并在材料张力的预测中验证模型效果。文献[19]优化GM(1,N)模型的时间响应函数,并预测我国未来CO2的排放量。

现有文献对灰色多变量模型参数优化及其拓展进行了较为深入的研究,一定程度上提升了多变量模型的建模效果,但实际应用中,优化模型及传统模型依然会存在较大的建模误差,产生上述问题的原因主要包括两个方面:①模型结构与系统行为特征的不匹配,灰色GM(1,N)模型及其改进模型在结构上均属于线性结构,而对于绝大多数实际问题系统的结构均呈现非线性特征,因此,利用线性结构模型解决非线性问题往往会产生不合理误差;②驱动因素作用的复杂性和不确定性,传统模型默认了驱动因素自始至终对主系统产生相同强度的作用效果,而实际系统运行过程中,随着系统自身及驱动因素的演化发展,各驱动因素在系统的不同发展阶段所发挥的作用不尽相同,不对各阶段驱动因素作用机制进行分析必然会导致较大的模型误差;因此,基于以上问题,作者在灰色建模机理基础上,提出多变量离散灰色幂模型,以非线性结构模型解决复杂的非线性预测问题,并基于各驱动因素在不同阶段对系统行为变量的差异化作用效果,构建多阶段驱动控制的多变量离散灰色幂模型,最后通过对我国粮食产量进行预测的案例,说明本文模型在解决非线性、多变量、少数据系统建模问题时的优越性和有效性。

1 多变量离散灰色幂模型的构建及其优化模型

1.1 多变量离散灰色幂模型构建及求解

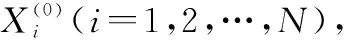
(1)

为多变量离散灰色幂模型,记为DGPM(1,N),其中b1,b2,…,bN+1为DGPM(1,N)模型的参数。

则参数列的最小二乘法估计满足:

(2)

(2) 模型的还原值为

(3)

上述新模型实现了差分形式与微分形式的统一,能够有效避免传统模型中二者间转换的跳跃性误差,并且依靠自身动态特性,反映驱动因素序列对系统行为变量的同步作用效果。若白化信息充分,即幂指数已知时,可以利用模型进行非线性建模预测。该模型能避免离散与连续模型转换时的误差,并利用非线性幂模型结构解决非线性问题。但从模型结构上看,该模型默认各驱动因素在系统运行过程中时刻对主系统行为序列产生同强度的影响,未考虑各阶段驱动因素作用效果的差异性。事实上,随着系统的演化发展,各时间阶段起主导作用的驱动因素可能会发生变化,各驱动因素作用时效和强度也不尽相同。因此,本文在DGPM(1,N)模型基础上,构造多阶段驱动控制的多变量离散灰色幂模型。

1.2 多阶段驱动控制的多变量离散灰色幂模型构建及求解

(4)

为多阶段驱动控制的多变量离散灰色幂模型,记为MDGPM(1,N),其中di+1(k)=μ(k-di+1,1)-μ(k-di+1,2),0≤di+1,1≤di+1,2为驱动因素Xi的控制项,μ(k)为阶跃函数,di+1,1,di+1,2分别为驱动因素Xi+1的开始和结束作用时间;γ=(γ2,γ3,…,γN)为幂指数,反应驱动因素对系统行为的非线性作用关系。

从定义2可以看出,MDGPM(1,N)模型为原DGPM(1,N)模型中的每个驱动因素添加了相应的驱动控制项di+1(k),di+1(k)为矩形函数,包含始末两个点参数di+1,1,di+1,2,通过对始末点参数的识别,能够判断该驱动因素对主系统行为的作用机制,真实反映建模意义。

证明当di+1,1=0且di+1,2→+∞时

di+1(k)=μ(k-di+1,1)-μ(k-di+1,2)=μ(k)

证毕

定理3表明,系统运行过程中,若所有驱动因素从开始至结束始终对系统行为序列产生强度相当的影响,则MDGPM(1,N)模型与DGPM(1,N)模型等价。进而表明本文模型是在驱动因素作用机制信息不断白化条件下对多变量模型的进一步拓展与丰富。

则参数列的最小二乘法估计满足:

(5)

(2) 模型的还原值为

(6)

证明(1)利用数学归纳法当k=1时,

结论成立。

假设当k=m时结论成立,即可得

根据定义2中的式(4)可以得到

因此,当k=m+1时结论也成立,故定理得证。

证毕

1.3 多变量离散灰色幂模型的幂指数优化

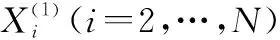
(1) 对于DGPM(1,N)型,可以通过以下非线性规划模型求解幂指数

(7)

(2) 对于MDGPM(1,N)模型,可以通过以下非线性模型求解幂指数

(8)

对于DGPM(1,N)模型,可以借助LINGO软件或者粒子群、遗传算法等智能算法求解最优幂指数γ=(γ2,γ3,…,γN),然后利用定理2进行建模预测。而对于MDGPM(1,N)模型,需要先对驱动控制项进行识别,之后才能进行幂指数优化,再利用定理5进行建模预测。关于多阶段驱动因素控制项识别方法,将在下节进行详细阐述。

2 驱动因素控制项识别及建模步骤

从上面的建模过程可以看出,驱动因素作用机制是影响MDGPM(1,N)模型精度的重要因素之一。在实际建模过程中,各驱动因素的始末作用时期和强度是未知的,需要通过不断增加白化信息来对各参数进行估计。因此,本文模型基于对已有白化信息的充分分析,探讨驱动控制项参数的识别路径。

2.1 多阶段驱动因素控制项参数识别方法

鉴于认知水平和理论有限,本文仅讨论了白化信息较为充分情况下驱动因素控制项的参数识别方法,而对于缺乏白化信息的情况,文献[12]则利用非线性优化建模,结合智能算法算法加以信息补全和参数识别,但该思路缺乏论述和理论依据,并且未在实例中加以讨论,实用性和有效性有待商榷。因此,本文将先对系统结构较为清晰状况下的驱动参数识别方法进行研究,后续将进一步探索信息匮乏情况下驱动参数识别。

当已知系统行为状态或驱动因素作用的白化信息,我们可以根据历史经验事先给出驱动因素作用信息。这类白化信息主要包括主导影响因素在不同时间阶段对主系统作用效果的变化,如不同时间阶段对粮食产量的影响主导因素变化、不同阶段对CO2排放影响的主导能源消费种类差异等等。这类影响因素作用效果发生变化的数据类型,本文提出的MDGPM(1,N)模型更有优势。针对这类数据类型,将主系统行为序列和驱动因素序列分为若干子序列,通过分析系统行为序列子序列与各驱动因素序列子序列间的相关性,确定主导驱动因素的作用机制。

定义3设点集P={P1,P2,…,Pm|1≤Pi≤n,},Pi为整数,将主系统行为序列和驱动因素序列Xi(i=1,…,N)划分为m+1个子序列,分别记为

(9)

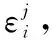
di(k)=μ(k-pj-1-1)-μ(k-pj)

若Xi为第j,j+1,…,j+q时段的主驱动因素序列,则di(k)=μ(k-pj-1-1)-μ(k-pj+q)

定义3根据掌握的白化信息,利用灰色关联分析方法,确定各时段上对主系统行为序列影响作用较大的主驱动因素,进而利用定义2获得的驱动因素控制函数,然后利用MDGPM(1,N)模型进行预测。当主系统行为信息较为充分,驱动因素作用机制较为明确时,该方法行之有效,具有较准确的实际应用意义。

大量研究表明，槐耳具有抗肿瘤活性，可以抑制血管及肿瘤形成、抗肿瘤耐药、抑制癌转移、激活免疫系统以及诱导凋亡等[10，11]。最近也有研究报告，槐耳清膏能诱导乳腺癌细胞发生自噬及凋亡，其机制可能是通过抑制MTOR/S6K通路有关[12]，另有研究结果表明，槐耳清膏对胃癌MKN-45细胞增值及凋亡均有影响[13]，但能否影响her-2阳性胃癌细胞自噬尚未见相关报道。

2.2 MDGPM(1,N)模型的建模步骤

综上所述,MDGPM(1,N)模型的建模与预测过程可以分为以下步骤:

步骤2若系统运行的白化信息较为充分,则根据定义3识别驱动因素控制项的时间参数和确定主要驱动因素,然后利用式(8)对幂指数进行优化求解。

步骤3根据定理4求解模型参数b,再依据定理5计算主系统行为序列的模拟值,并进行精度效果检验。若误差超出许可范围,转入步骤1,重新分析驱动因素及控制参数。

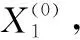
3 实例分析

对我国粮食产量进行准确高效地预测,有利于实现新常态下我国经济的稳定增长。通过研究我国粮食产量现有历史数据可以发现,我国粮食产量的发展由于经历了多种因素的影响,呈现出波动增长的态势。为了能准确分析近阶段我国粮食产量发展的趋势,我们主要研究2003年以后我国粮食产量的变化。2003年以后,由于中央认识到以前政策措施存在的不足,积极调整政策,使得我国粮食产量一直保持稳定增长。尤其是以2008年为转折点,当年我国全面取消农业税,9亿中国农民的种粮积极性收到极大鼓舞。并且,中央财政还持续加大强农惠农支持力度,实行粮食生产补贴等一系列惠农政策。因此,建立模型时,充分考虑我们粮食产量增长的特点,选择2003-2015年数据为模拟预测数据,并以2007年为分界点对我国粮食产量进行建模研究。

为了检验本文模型的效果,以2003-2013年数据作为建模数据,2014-2015年数据作为检验数据,数据来源为《中国统计年鉴》。通过对历史文献资料的研究发现,对粮食产量产生影响的因素及其测量值如表1所示,记粮食产量(万吨)、耕地灌溉面积(千公顷)、农业机械总动力(万千瓦)、化肥施用量(万吨)、粮食播种面积(千公顷)分别为X1～X5。为了避免不同指标数据数量级差异带来的模型建模误差,在建模前需对数据进行初值化变换,所有建模过程均采用变换后的数据,获得模拟预测结果后,再进行数据还原处理。初值化后数据如图1所示,从中可以看出粮食产量与各影响因素间呈现典型的非线性特征,因此比较适合本文模型进行建模。根据定义2建立MDGPM(1,N)模型为

(10)

图1 系统行为变量和驱动因素初值化后的趋势图Fig.1 Initialized values of system behavior variable and driving factors

通过上述分析可知,粮食产量序列和各驱动因素序列的白化信息比较充分,可以利用定义3识别主驱动因素及其作用控制项函数。因此,以2007年为分界年,分别研究2003-2007年、2008-2012年各驱动因素对粮食产量的影响程度,计算各驱动因素与粮食产量的关联度见表2。

表2 各驱动因素与粮食产量的关联度计算结果

关联度阈值选为r=0.75。根据定义5可知,2003-2007年间对粮食产量影响较大的驱动因素为X3和X4,而2008-2013年的主驱动因素为X2和X4。驱动因素作用机制分析结果表明,2003-2007年间农业机械化和化肥使用程度的提升是粮食产量增加的主要影响因素,而2008年之后,农业机械化达到一定规模后,随着农业机械化程度达到一定水平后会出现边际效应递减现象;随着我国人口的快速增长对粮食需求的增加,以及伴随着工业化和城市化的不断推进,造成灌溉水资源出现短缺,使得耕地灌溉面积成为新时期影响粮食产量的重要因素。而作为化肥使用,一直是我国粮食产量保持增长趋势的基础,随着化肥技术和品质的不断提升,土地贫瘠现象的加重,粮食产量对其依赖程度也不断提高,这与我国当前农业种植现状是比较吻合的。根据以上分析,可以得到各驱动因素的控制函数为

因此,式(10)所示模型转化为

(11)

根据定理4求得模型参数为

b1=-1.027 2,b2=-0.014,b3=-0.001,

b4=0.002 2,b6=1.067 6

γ2=0.357 9,γ3=1.995 3,γ4=1.144 4

MDGPM(1,N)模型为

(12)

根据上述拓展模型模拟2003-2013年粮食产量结果如表3所示,再利用2014-2015年的X2和X4数据,代入式(12)进行粮食产量预测。为了对比模型的性能,本文还选取了DGPM(1,N)、GM(1,N)和DGM(1,N)建模,所得模型分别为

DGPM(1,N)模型为

GM(1,N)模型的白化方程为

DGM(1,N)模型为

表3 4种模型模拟和预测结果

4个模型的建模效果对比如图2所示。

从各模型的建模效果来看,本文提出的多变量离散灰色幂模型在模拟和预测阶段均取得了较好的精度,在充分分析驱动因素对粮食产量作用机制的基础上,进一步提高了建模精度。离散DGPM(1,N)模型的两项误差分别为2.35%和5.72%,实现了高精度的平稳模拟和预测。在对驱动因素进行多阶段划分后,识别两阶段的主导因素并建模,取得了模拟和预测误差分别为0.65%和3.39%的良好效果,远高于其他3种模型。鉴于本文在通过均值化处理建模数据后,数据变动幅度不大,使得传统GM(1,N)模型也取得了不错的预测效果,但对于影响因素变幅较大的数据序列GM(1,N)模型难以适应,不满足其建模假设条件,这些在以往文献中已得到验证[20]。而多变量离散模型,虽然一定程度上能克服模型转化误差,但其未充分考虑驱动因素的多阶段特征,并且适合具有固定增长速度的序列建模,对于呈现非线性特征的序列建模性能较差,因此建模平均误差为10.27%,预测误差为9.87%,不适合用于粮食产量预测。另外,从图2的误差分布图可看出,两种传统多变量模型精度波动程度大于本文的两种多变量离散幂模型,预测效果不稳定。因此,综合对比4种模型模拟预测效果和误差分布图,通过分析粮食产量驱动因素的多阶段作用机制,构建非线性结构的多变量灰色幂模型,能够持续降低建模和预测误差,本文方法更适合用于我国粮食产量的未来预测。

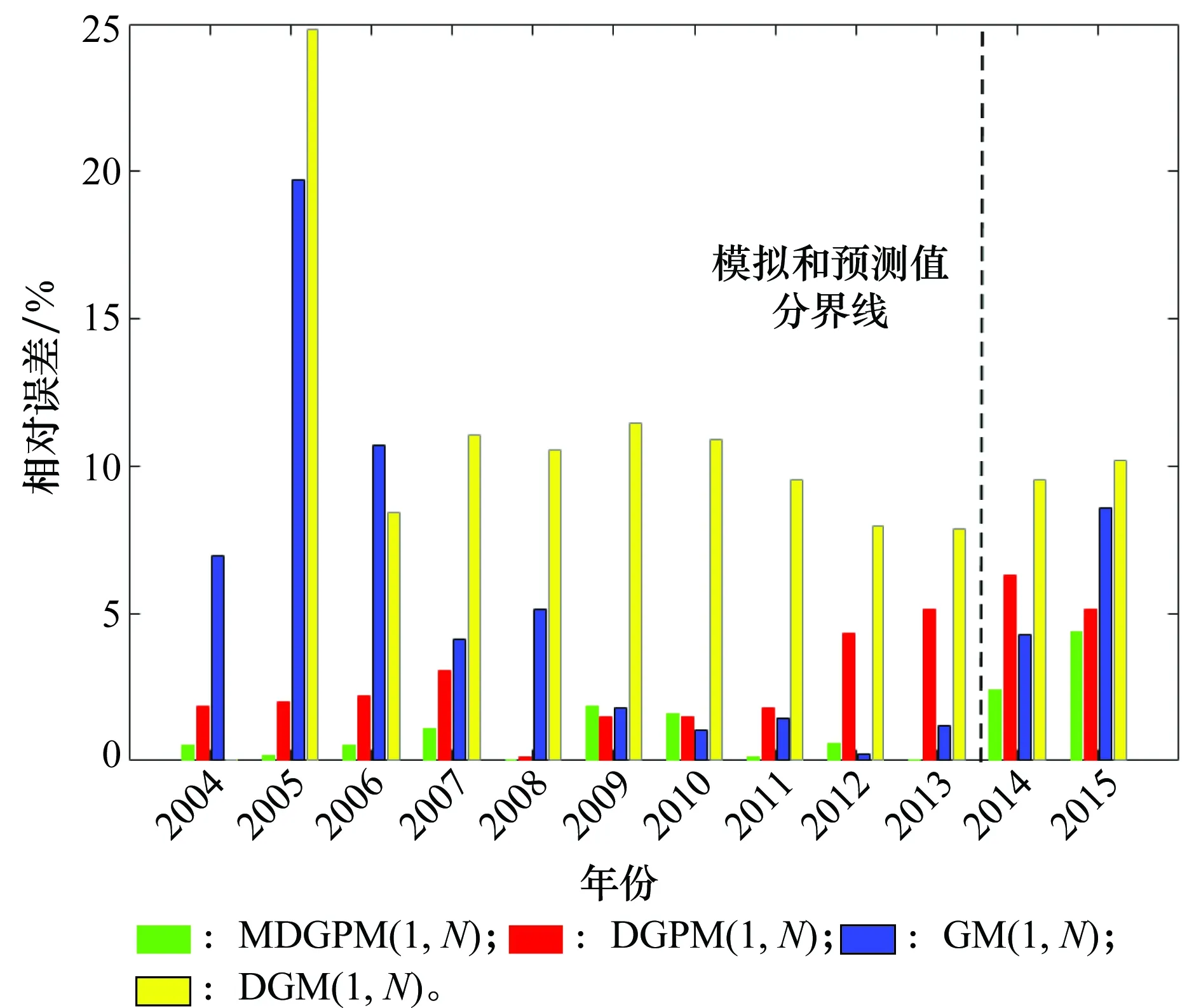
图2 4种模型模拟和预测误差分布图Fig.2 Error analysis of the four competing models

4 结 论

多变量灰色预测模型是解决多变量少数据系统预测问题的重要途径,通过不断白化系统信息,找到系统行为趋势规律,进而通过微分方程进行模拟和预测。针对现实生活中广泛存在的非线性多变量系统预测问题,本文将传统的多变量灰色离散模型拓展为含有幂指数项的离散模型,并探索幂指数及模型参数的求解路径,克服过去利用线性结构模型解决非线性问题的局限。通过对系统行为序列和驱动因素序列的多阶段划分,明晰各阶段驱动因素的作用机制,并且在利用平均相对误差最小条件下非线性约束模型对参数进行识别,求解驱动控制参数和体现非线性作用的最优幂指数。最后,通过对我国粮食产量的数据进行建模,发现本文MDGPM(1,N)模型能够有效识别不同阶段主导因素作用效果差异,更精确描述我国粮食产量与各影响因素间的非线性作用关系,进而显著改善对我国粮食产量模拟和预测效果。未来,可以开展对信息缺乏时驱动因素作用项的识别研究,将灰度信息白化或结合其他智能手段确定驱动参数,进一步拓展新模型的应用范围。

参考文献：

[1] 党耀国,米传民,钱吴永.应用多元统计分析[M].北京:清华大学出版社,2012.

DANG Y G. MI C M. QIAN W Y. Applied multivariate statistical analysis[M]. Beijing: Tsinghua University Press, 2012.

[2] DENG J L. The control problem of grey systems[J]. System Control Letter, 1982, 1(5): 288-294.

[3] 刘思峰,党耀国,方志耕.灰色系统理论及其应用[M].北京:科学出版社,2010.

LIU S F, DANG Y G, FANG Z G. Grey system theory and its application[M]. Beijing: Science Press, 2010.

[4] 肖新平,宋中民,李峰.灰色技术基础及其应用[M].北京:科学出版社,2005.

XIAO X P, SONG Z M, LI F. Grey technology and its application[M]. Beijing: Science Press, 2005.

[5] GUO H, XIAO X P, FORREST J. A research on a comprehensive adaptive grey prediction model CAGM(1,N)[J]. Applied Mathematics and Computation, 2013, 225(1): 216-227.

[6] TIEN T L. The indirect measurement of tensile strength of material by the grey prediction model GMC(1,N)[J]. Measurement Science Technology 2005, 16(16): 1322-1328.

[7] TIEN T L. Forecasting CO2 output from gas furnace by grey prediction model IGMC(1,N)[J]. Journal of the Chinese Society of Mechanical Engineers, 2010, 31(1): 55-65.

[8] TIEN T L. The indirect measurement of tensile strength by the new model FGMC(1,N)[J].Measurement, 2011, 44(10): 1884-1897.

[9] 何满喜,王勤.基于Simpson公式的GM(1,N)建模的新算法[J].系统工程理论与实践,2013, 33(1): 199-202.

HE M X, WANG Q. New algorithm for GM(1,N) modeling based on Simpson formula[J]. Systems Engineering-Theory & Practice, 2013, 33(1): 199-202.

[10] ZHANG K. Multivariate discrete grey model base on dummy drivers[J].Grey Systems:Theory and Application,2016,6(2): 246-258.

[11] 丁松,党耀国,徐宁.基于驱动变量增长趋势的TGM(1,N)预测模型[J].系统工程,2015,33(3):149-153.

DING S, DANG Y G, XU N. TGM(1,N) prediction model based on trends of driving variables[J]. Systems Engineering, 2015, 33(3): 149-153.

[12] 张可.基于驱动控制的多变量离散灰色模型[J]. 系统工程理论与实践, 2014, 34(8): 2084-2091.

ZHANG K. Multi-variables discrete grey model based on driver control[J].Systems Engineering-Theory & Practice,2014,34(8):2084-2091.

[13] ZENG B, LUO C, LIU S, et al. A novel multi-variable grey forecasting model and its application in forecasting the amount of motor vehicles in Beijing[J]. Computers & Industrial Engineering,2016,101:479-489.

[14] 谢乃明,刘思峰.多变量离散灰色模型及其性质[J].系统工程理论与实践,2008,28(6): 143-150.

XIE N M, LIU S F. Research on the discrete grey model of multi-variables and its properties[J]. Systems Engineering-Theory & Practice, 2008, 28(6): 143-150.

[15] 张可, 曲品品. 时滞多变量离散灰色模型及其应用[J]. 系统工程理论与实践, 2015, 35(8): 2092-2103.

ZHANG K, QU P P. Delay multi-variables discrete grey model and its application[J]. Systems Engineering-Theory & Practice, 2015, 35(8): 2092-2103.

[16] 毛树华,高明运,肖新平. 分数阶累加时滞GM(1,N,τ)模型及其应用[J]. 系统工程理论与实践, 2015, 35(2): 430-436.

MAO S H, GAO M Y, XIAO X P. Fractional order accumulation time-lag GM(1,N,τ) model and its application[J]. Systems Engineering-Theory & Practice, 2015, 35(2): 430-436.

[17] WANG Z X, YE D J. Forecasting Chinese carbon emissions from fossil energy consumption using non-linear grey multivariable models[J].Journal of Cleaner Production, 2017, 142: 600-612.

[18] ZENG B, LUO C, LIU S, et al. Development of an optimization method for the GM(1,N) model[J]. Engineering Applications of Artificial Intelligence, 2016, 55: 353-362.

[19] DING S, DANG Y G, LI X M, et al. Forecasting Chinese CO2 emissions from fuel combustion using a novel grey multivariable model[J].Journal of Cleaner Production,2017,162:1527-1538.

[20] PAI T, CHIOU R, WEN H. Evaluating impact level of different factors in environmental impact assessment for incinerator plants using GM(1,N) model[J].Waste Management,2008,28(10): 1915-1922.