基于多结构元素形态滤波和EMD的轴承故障诊断*
郑小霞,贾文慧,王靖,任浩翰
(1.上海电力学院 自动化工程学院,上海 200090;2.上海东海风力发电有限公司,上海 200090)
0 引言
滚动轴承作为海上风电机组的关键零件,其健康状况对整个风机的运行状况会产生很大影响,据统计,约 29%左右的机械故障与轴承损伤有关[1]。因此,需要对滚动轴承进行及时的状态监测和故障诊断。而在实际情况下,设备的工况十分复杂、伴随其启动过程会出现强转速波动而且发生故障时会有冲击干扰,所以获取到的振动信号会被多种噪声污染[2]。因此在故障诊断前需要先对要研究的信号进行降噪处理。
形态滤波被称为一类新型非线性滤波方法,具有很强的脉冲干扰抑制能力,所以被广泛运用于信号处理中。胡爱军等提出了单一尺度结构元素的形态学滤波器,用于去除振动信号的噪声[3];姜万录等提出了一种迭代自适应多尺度形态分析(IAMMA)的滤波方法,对振动信号进行多尺度形态差值迭代运算,达到滤除噪声成分的目的[4];刘俊峰等引入了一种多结构元素的滤波方法对大地电磁中的噪声进行消除[5]。但上述形态滤波方法应用于含多噪声的实际振动信号分析时,在结构元素与尺度的选择上都存在各自的局限性,当前仍欠缺将其两者有效结合的方式。经验模态分解(Empirical Mode Decomposition,EMD)是由Huang等人提出的一种非线性时频分析方法[6],在信号特征获取方面具有独特的优势,近年来被广泛运用于轴承的故障诊断中[7-8]。
本文针对实际现场振动信号的特点,在单一元素多尺度形态滤波的基础上进行改进,提出了多结构元素的多尺度形态滤波的方法,并运用EMD分解法对滤波后的信号处理,获得更加准确的固有模态函数( Intrinsic Mode Function,IMF) 分量,以到达准确诊断的目的。并将构造的方法运用到标准以及实际海上风机的轴承故障诊断中,其诊断结果证明了此方法是有效的。
1 多结构元素的多尺度形态滤波
数学形态学通常以集合来描述目标信号,其思想是找到合适的某种形态元素来量度并获取非线性信号中的形状,考察信号各部分之间的联系,从而达到对信号综合分析、全面识别并从中选取有效信号的目的[9]。目前普遍应用的是多尺度形态滤波器,这种方法在组合的过程中,仅选用一种结构元素,因此可针对性的去除某种噪声。而从现场风机所获取到的实际信号经常会受到不止一种噪声的干扰(如脉冲噪声、白噪声等),该滤波器无法达到全面滤波的效果。因此本文基于多尺度滤波的思想,构造了由几个不同结构元素的多尺度滤波器组合成的滤波器,可以利用不同元素的特点更好的滤除多种噪声,便于进行故障的诊断。
1.1 形态滤波器的构造
考虑到不同结构元素对噪声敏感度不同的特点,根据实际风电采集的振动数据包含噪声的多样性,构造了由多个结构元素组合而成的形态滤波器,如图1所示。
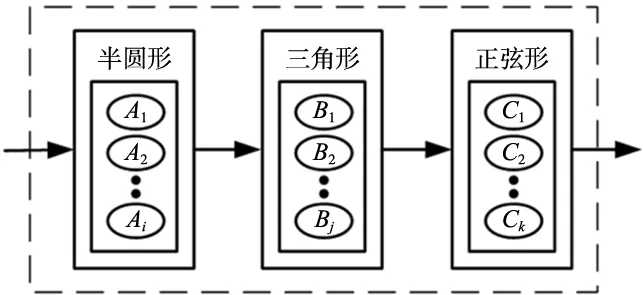
图1 多结构元素的多尺度形态滤波器
图1中A1~Ai表示半圆形的多尺度滤波器,B1~Bj表示三角形的多尺度滤波器,C1~Ck表示正弦形的多尺度滤波器。首先利用半圆形结构元素的不同尺度的形态滤波器对信号进行处理,然后按照一定的权重系数将不同尺度得到的结果进行组合,得到新的信号,并将其作为下一个结构元素三角形的输入信号,重复上述过程,直至正弦形结构元素对信号进行处理,得到的结果即为降噪处理后的信号。
选取不同大小的i元素各自对原始信号数据滤波,设有s个结构元素,尺度分别设为i={i1,i2,…,in},可得到n个尺度下的系列处理信号:
(1)
将不同的尺度处理后的数据信号按照一定的权重组合,由此i元素的输出数据信号可表示为:
(2)
式中,wik为各尺度下的权重系数,eik为各尺度下滤波误差。
1.2 结构元素的选取
形态滤波的效果与结构元素的选取有很大的关系,应依据原始信号数据的特点和要突出信息的特征来选择具体的形状和尺度。
(1)结构元素形状的选取
不同的结构元素对各类的噪声敏感度不同,一般最好选择具有某种凸性的结构元素,如圆形、三角形,正弦形等,其滤波的能力较强,而且不同的元素其针对的噪声类别也不同。例如:要想更好的去除白噪声,一般选用半圆形的元素,而三角形的元素主要针对脉冲噪声;振动信号一般会周期性变化,类似于正弦信号,故需要一个正弦形的滤波器。综上考虑本文利用三种不同元素(半圆形、三角形、正弦形)的滤波器进行级联,以达到全面滤波的效果。
(2)结构元素尺度的选取
在数学形态滤波中,结构元素的大小与噪声分量的大小是相互对应的,即尺度较大的元素可以滤除大分量干扰,反之也成立。而元素复杂度增加,长度增大,计算量也会随之增大;反之则减小。本文根据信号中待提取的信号特征信息,选取合适的n个尺度,进行组合滤波,产生n个形态滤波分量,按照公式(2)进行组合,避免在结构元素长度选取过程中的偶然性误差。
1.3 滤波性能判别指标
当轴承发生故障时,各因素的影响将产生周期性冲击信号,峭度、偏斜度等对冲击信号都特别敏感,是评判轴承故障特征提取能力的重要指标。文献[10]中对正常状态和故障状态的齿轮信号进行时域分析,计算7个时域特征并作图,从图中可以看出偏斜度的变化幅度很小,很难进行判断。由于风电场现场环境比较恶劣,所测得的振动信号除包含有用的特征信息外还存在大量的噪声干扰,信噪比和均方根误差是评价去噪性能的常用指标。文献[11]中运用信噪比作为评价其去噪性能的唯一指标,在基于系数校正的改进阈值去噪的算法中,与标准算法相比,使用软阈值时,信噪比只增加了0.3632dB,使用硬阈值时增加了0.6042 dB,其变化不是很明显。本文选用信噪比与偏斜度定义了一个新的指标J,用来判定去噪的性能,其公式如下:
(3)

2 故障诊断流程
EMD是一种普遍运用于分析非线性、非平稳信号的时频处理方法,其依据信号自身的局部特征信息进行自适应分解,得到一系列具有不同时间特征尺度的IMF,能够进行自适应的多分辨率分析[12]。本文引入EMD对形态滤波去噪后的信号进行处理,进而判断故障的具体类型,其具体流程如图2所示。

图2 故障诊断流程
(1)根据原始信号的特点选择合适的结构元素和尺度构造多结构元素的多尺度形态滤波器。
(2)利用(1)中构造的形态滤波器对信号进行降噪预处理,去除信号中多余的噪声信号,为故障诊断做准备。
(3)计算去噪后信号的全部极值点,并用三次样条插值的方法对极值序列进行处理,得到信号的两条包络线e+(t)和e-(t)。
(4)计算平均包络线:m(t)=[e+(t)+e-(t)]/2,并提取信号的细节d(t)=x(t)-m(t)。
(5)判断是否符合IMF的两个条件,若不符合则记x(t)=d(t),重复进行步骤(3)~步骤(5),直到满足条件为止。此时,d(t)为一个IMF,记为imf1。
(6)记残余分量r1(t)=x(t)-imf1为新的待分解信号,重复步骤(3)~步骤(5),得到第二个IMF,记imf2,此时,余项为r2(t)=r1(t)-imf2。反复进行以上的过程,直至残余部分ri(t)满足永远单调变化或者总小于某一阈值的条件时,该分解过程结束。
(7)对上述得到的IMF做包络分析,得到其包络谱图,从中找出可以表征故障具体类型的特征频率,进而判断故障的具体类型。
3 仿真研究
为了验证本文所提出的方法可以有效的去除噪声以及其与EMD结合后可以准确的进行故障诊断,利用美国凯斯西储大学(CWRU)实验室的标准振动信号数据和某风电场实际采集到的信号进行仿真验证。
3.1 标准轴承信号仿真分析
本文采用的是标准轴承振动信号数据,具体选定在带有一马力的负荷状况下,轴的转动速度为1772r/min,其中传感器采样频率为12000Hz。通过传感器和编码器采集的振动信号时域波形以及对其进行传统的FFT分析后的幅值谱图如图3所示。故障制造在滚动轴承的外圈部位,故障的直径为21mils,图4为发生故障情况下,信号的时域波形以及FFT变换后的频谱。

图3 正常信号的时域波形和频谱
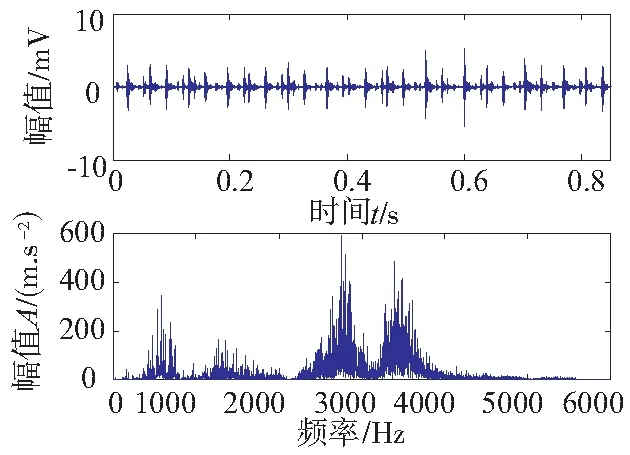
图4 故障信号的时域波形和频谱
从图3中可以看出正常工作时,其时域波形平稳,没有大波动。而图4中存在很大的周期性冲击脉冲,使得信号的振动幅度变大,形成了一串震荡的阻尼衰减波,因此可以初步判断其运行在故障状态。根据相关的公式可以得到轴承的故障频率分别为:外圈104.56Hz,内圈157.94Hz,滚动体137.48Hz。运用EMD对该信号处理,可以得出IMF的包络谱图如图5所示。

图5 故障信号IMF包络图
图5中出现频率为106.2Hz,135.5Hz,153.1Hz的信号,与外圈、内圈和滚动体的故障频率相近似,无法准确判断其故障的具体类型。
根据形态滤波结构元素宽度和高度的选取原则及标准轴承信号的特点,多次试验选取L=3~12。运用多结构元素的多尺度形态滤波对故障信号进行处理,得出其信噪比,偏斜度,以及诊断因子的值如表1所示。

表1 判别指标
由表1可得,与单元素的形态滤波器相比,运用本文的方法可使信噪比增大,偏斜度减小,判别指标J也有明显的提高,由此表明该方法的滤波效果更好。用EMD方法对噪声去除后的信号分解分析,可以得出 IMF的包络谱图,如图6所示。

图6 形态滤波—EMD后的IMF包络图
与图5相比,从图6中可以看出频率为106.2Hz 的信号特别突出,与外圈故障时所求得的特征频率104.56Hz相近,由此可以判断为轴承外圈故障,进而可以看出该方法可以降低信号中的噪声,提取出有效信号。
3.2 实际海上风电场轴承信号仿真分析
本文采用的实际现场数据是某海上风机的轴承数据。当时发电机平均转速为680r/min),通过计算可以得出轴承的故障频率分别为:外圈40.6277Hz,内圈为61.3723Hz,滚动体 53.4197Hz。图7为某天下午5点轴承信号时域的波形以及FFT变换后的频谱。

图7 风电场实际信号时域波形和频谱
从图7中可以看出其波形中有周期性冲击信号,但不是很明显,频率能量分部不是十分集中,可以判断轴承处于故障初期状态。运用EMD对上述信号进行处理,可以得出其IMF的包络谱如图8所示。
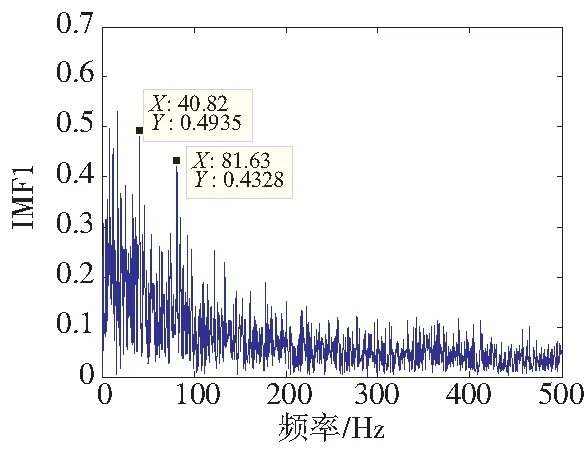
图8 EMD分解后的IMF包络谱图
从图8中能找到外圈故障的特征频率,但含有其它分量,无法准确诊断其故障的具体类型。按照形态滤波选择结构元素尺度时的原则及实际风机数据的特征,多次试验选定L=3~8。对信号进行多结构元素的多尺度形态滤波处理,得出其信噪比,偏斜度,以及判别指标的值如表2所示。

表2 判别指标
由表2可得出,与单元素的形态滤波器相比,运用本文方法处理后信噪比增大,偏斜度减小,进而判别指标J也有明显的提高,由此说明该方法的去噪效果更好。运用EMD方法对噪声去除过的信号进行分解,可以得出其IMF的包络谱,如图9所示。

图9 形态滤波—EMD后的IMF包络图
与图8进行对比,图9中可以更明显的突出40.82Hz的信号,而且其二倍频,三倍频的信号均有出现,所以可以准确判断轴承为外圈故障,与后期现场故障记录显示的该机组存在外圈故障相一致,进而验证了与单一元素的多尺度形态滤波方法相比,本文方法可以有效的去除噪声信号,进行准确的故障诊断。
4 结束语
为解决海上风电场现场釆集到的实际振动信号受到多种噪声干扰的问题,本文提出了多结构元素的多尺度形态滤波算法,并将其与EMD结合用于轴承的故障诊断。诊断结果表明: 该算法与单元素的形态滤波方法相比,能更好的抑制噪声,减少噪声的干扰,提高了EMD分解的准确度,进而更精确地得到关于故障特征的信息,可以更确切的判断出所发生故障的具体类型。
[参考文献]
[1] 胡耀斌, 厉善元, 胡良斌. 基于神经网络的滚动轴承故障诊断方法的研究[J]. 机械设计与制造, 2012(2):187-189.
[2] 曹冲锋, 杨世锡, 杨将新. 大型旋转机械非平稳振动信号的EEMD降噪方法[J]. 振动与冲击, 2009, 28(9):33-38.
[3] 胡爱军,唐贵基,安连锁.基于数学形态学的旋转机械振动信号降噪方法[J].机械工程学报,2006,42(4):127-130.
[4] 姜万录,李扬,郑直,等. 基于迭代自适应多尺度形态滤波的滚动轴承故障诊断[J]. 中国机械工程,2015(23):3192-3199.
[5] 刘俊峰, 邓居智, 陈辉,等. 基于多结构元素形态滤波的大地电磁去噪[J]. 物探与化探, 2014(1):109-114.
[6] Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A Mathematical Physical & Engineering Sciences,1998,454(1971):903-995.
[7] 王龙, 沈艳霞, 季凌燕. 基于小波降噪和EMD方法的风力发电系统齿轮箱故障诊断[J]. 江南大学学报:自然科学版, 2012, 11(2):159-162.
[8] 王录雁, 王强, 张梅军,等. 基于EMD的滚动轴承故障灰色诊断方法[J]. 振动与冲击, 2014(3):197-202.
[9] 赵春晖,孙圣和. 一类多结构元素并行复合形态滤波器[J]. 哈尔滨工业大学学报,1997,29(2):64-67.
[10] 刘旭鹏.基于振动信号分析的旋转机械故障诊断方法研究[D]. 天津:天津理工大学,2014.
[11] 焦新涛. 小波分析及其在齿轮箱故障诊断中应用研究[D].广州:华南理工大学,2014.
[12] 王少锋, 王戈, 王建国,等. 基于EMD与自相关的能量算子解调机械故障诊断[J]. 机械设计与制造, 2016(6):174-178.

