高功率密度柴油机气门间隙故障信号提取
畅志明,续彦芳,杨海涛,傅湘雨,杨贵春
(1.中北大学 能源动力工程学院,太原 030051;2.中国北方发动机研究所,天津 300400)
0 引言
高功率密度柴油机包含很多的运动机构的同时其结构紧凑复杂。工作过程中振动激励源多、频率分布广, 平时长时间,高负载,如果采用直接测量法得到的振动信号是一个典型的非平稳信号[1-2]。目前大多数对内燃机的振动信号特征提取方法适用于一些单缸,激励源少的内燃机的简易故障诊断。但是对高功率密度柴油机振动信号处理和提取效果不是很理想[3]。而且一般的信号处理方法, 对提取出的故障特征表征具有模糊性, 不能直观地分辨出故障的类型, 本文应用以模糊数学为理论基础的聚类分析方法结合信息熵进行特征提取为解决此类模糊性问题提供了一种新的途径。
1 实验方案设计
本实验以某高功率密度柴油机为研究对象,对其缸盖上端面布置测试点进行信号采集,测试与处理系统如图1所示。该测试点选取是根据内部主要构件活塞高速运动冲击,进气门开启及关闭撞击的基本运动形态,结合内燃机固有振动特性和传递关系,进行测点优化布置,最终在内燃机第6缸盖上端面上布置测点。采用经过机械滤波器处理的耐高温加速度传感器,避开阻尼部件,对内燃机的燃烧过程产生的冲击振动进行测试。同时,在喷油泵齿轮轴上安装脉冲传感器采用频率20kHz的等时间采样方法来标定1 缸压缩上止点。在测试过程中将第6缸排气门间隙设置为0.4,0.5,0.6,0.7mm,通过对气门间隙微调影响其工作状况。其中0.4mm为正常状态。
在实验中选用了计算机便携式DASP (Data Acquisition & Signal Processing-数据采集和信号处理) 系统采集记录测点的冲击加速度响应信号。
本实验进行空负载下不同的气门间隙造成的不同的信号振动。按照正常气门间隙、故障气门间隙一、故障气门间隙二、故障气门间隙三,4种工况依次进行工作,采集内燃机振动信号。
2 内燃机信号预处理
4种工况下内燃机振动信号采样点数如图2所示。

(a)正常 (b) 故障一

(c) 故障二 (d) 故障三图1 内燃机振动信号Y方向时域图
从图1可以看出,高功率密度柴油机的振动信号具有很强短时、瞬态、冲击特性,能量在燃烧后出现峰值,然后开始衰减。如果采用传统的经验模态分解(EMD),会导致固有模态分量(IMF)存在着比较严重的模态混叠现象。本文所用的EEMD 是经验模态分解的改进算法,利用了高斯白噪声具有频率均匀分布的统计特性。在原始振动信号中加入高斯白噪声,信号将表现在不同尺度上的连续性,促进了信号的抗混分解[4-6],有效解决了EMD方法中由于IMF的不连续性而造成的模式混淆现象。使用聚合经验模态分解的方法来进行降噪预处理使后续的信号表达出更为有用的信息。
2.1 EEMD分解步骤
(1)首先对总体的平均次数M进行初始化,后加入白噪声幅值,m=1;
(2)对原始振动信号应用EMD处理,进行第m次分解。
①对已知的幅值白噪声nm(t)叠加在信号x(t)上:
xm(t)=x(t)+nm(t)
(1)
xm(t)的意义为第m次加噪后的信号;nm(t)代表第m次加入的白噪声。
②用经验模态分解加噪信号xm(t),可以得到一组IMF分量cm,n(n=1,2,3…N)。其中cm,n为第m次分解得到的第n个IMF分量。
③如果m (2) 其中,n=1,2,3,…,N,m=1,2,…,M。 (3)记录N个IMF分量M次分解的平均值yn,最终作为的IMF分量[7-8]。 图2 正常工况时内燃机缸盖振动信号EEMD分解结果 以正常气门间隙柴油机机振动信号为例,经过简单的去趋势项后采用EEMD对振动信号进行分解得到各IMF分量,但各分量也包含一些噪声等非有用信号,通过IMF分量与原始信的相关性来选取需要重构的IMF分量,提高重构信号的有效性。采用EEMD对振动信号进行分解后如图2所示。 其中各IMF分量和原始振动信号的相关系数Rx,RIMF1…RIMFK,其计算公式如下: (3) 归一化计算公式为: (4) 其中,N—信号点数;j—第j个IMF量。 通过式中分析,分量与原始信的相关性来选取需要重构的IMF分量,来达到提高重构信号的有效性的效果。本文采用EEMD对振动信号进行分解,计算各分量与原始信号的自相关系数。通过每种工况下随机进行 4 次测试,在12个实验的样本中提取的特征参数,如表1所示。表中 1~3 为排气门间隙0.4mm时的数据; 4~6为排气门间隙0.5mm时的数据; 7~9为排气门间隙0.6 mm; 9~12为排气门间隙0.7 mm时的数据。 表1 不同样本特征参数对比 表1显示出, 在同一工况下采集的不同样本, 通过聚合经验模态分解以后, 能量的分布有一定的相似性。但是,经不同工况下采集的振动信号通过聚合经验模态分解以后, 其中相应层的能量分布表达出一定的差异性。对不同工况下的信号聚合经验模态分解后, 相应层代表的物理意义表现为一定的差异性,与不经任何处理的信号中提取气门间隙的故障特征相比, 利用聚合经验模态的预处理方法能够在样本容量有限的情况下增加故障特征向量的维数, 为提高故障识别的准确率奠定基础。 由于内燃机工作时的振动信号是非线性的而且有一定的分形特征。同时分形维数可以在一定程度上刻画信号填充空间的能力,假如其中信号发生某些干扰,导致了填充空间的能力就会发生变化,同时导致信号的分形维数就也会发生相应的变化。所以在高功率密度内燃机的故障诊断中引进分型几何来提取信号的结构特征——分形维数,可作为一种有广泛发展前景的故障诊断方法。目前研究理论来讲,单重分形的分形维数一般包括:豪斯道夫(Hausdorff)维数、信息维数、自相似维数、盒维数、关联维数、李雅普诺夫(Lyapunov)维数等。因为关联维数可以很好地反映时间序列的动态过程,但噪声对关联维数的影响比较大。因此通过采用EEMD方法将内燃机的振动信号分解为不同频段的IMF分量来提取关联维数。 模糊熵一般定义为[9]: (1)其中对N点序列{u(i):1≤i≤N}构造m维向量: (5) (6) (3)表达函数: (7) (4)定义模糊熵为: (8) 当N为有限值时,式(8)表示为: FuzzyEn(m,n,r,N)=lnφm(n,r)-lnφm+1(n,r) (9) 通过上式可以发现,模式维数m和相似容限r贯穿整个计算过程,因此,他们的选择对于模糊熵的计算非常重要。通过大量实验表明,m=1或2,r=0.1Std~0.25Std(Std是x(i),i=1,2,…,N的标准差)才能保证有效的统计特性和较小的误差。 依据采样定理,为保证信号采样后不失真,采样频率须大于信号中最高频率两倍。实验采样频率为20kHz,故N=200故取m=2,r=0.2Std,为获取尽量多信息,计算式取较小的整数值,故取n=2。 图3分别为正常,故障1,故障2和故障3四种工况原始振动信号的关联维数。由图3可知原始振动信号关联维数存在比较严重地混叠现象,区分困难。 图3 原始振动信号的关联维数 图4是原始振动信号经过EEMD分解重构后的关联维数。可以看出,经过EEMD分解后选取的分量对故障特征信息的干预的噪声起到了抑制作用,在图中可以明显看出低嵌入维数和嵌入维数2~16之间可以实现有效的分离,四种工况的关联维数可以实现良好的分类识别并且区分明显。 图4 EEMD分解重构的关联维数 同时,经过分析四种工况的原始信号的模糊熵同样存在很大的交叉和重叠,图6列出聚合经验模态法分解后的第一个IMF分量的模糊熵。由图5可知,经过聚合经验模态法分解后,各种工况之间第一个IMF分量模糊熵可以明显地表现信号的特征。正常工况的IMF分量模糊熵最大,这是因为在内燃机正常工况下的振动信号随机性大,无规律,模糊熵最大。 图5 第一个IMF分量的模糊熵 最后,本文通过采用嵌入维数为10的关联维数和分量的模糊熵组成组合特征向量来进行高功率密度柴油机的气门间隙故障诊断。通过组合特征参量(每种工况八组数据,共32组)取每种工况的前四组数据,共16组数据作为训练样本对RBF神经网络进行训练,其余16组作为测试样本,进行测试,诊断正确率为87.5%。下表为分别采用模糊熵、分形维数和组合特征三种不同参数性能比较。由表可知,应用EEMD分形维数模糊熵的气门间隙故障诊断方法的精确率更高。 表2 采用不同特征参数的性能对比 % 通过聚合经验模态分解得到的相关系数区分性较强,能十分有效区分真实IMF分量和包含噪声的IMF分量,将真实分量重构达到了降噪的目的。分析柴油机气门间隙故障振动信号分析结果表明: EEMD 对解决非线性、非平稳问题具有很好的效果, 经过 EEMD 分解后得到的各 IMF 突出了原信号不同的局部特征信息, 通过对各 IMF 的分析, 提取出能够描述故障信息的特征变量即各层所占能量比该能量比可以有效地描述不同振动故障特征, 结合分形模糊熵特征值, 能准确地对高功率密度柴油机气门间隙进行状态识别与故障诊断, 同时对内燃机的其他复杂故障的特征提取和故障诊断提供了新的手段。 [参考文献] [1] 吴震宇,袁惠群,李沈. 基于EMD和模糊聚类的柴油机故障诊断[J]. 东北大学学报(自然科学版),2009,30(12):1784-1787. [2] 张俊红,王健,毕凤荣,等. 基于EMD和时频分析的低振动机体结构优化研究[J]. 振动与冲击,2014,33(3):117-144. [3] S Deng,Seng-Yi Lin,We-Luan Chang. Application of Multiclass Support Vector Machines for Fault Diagnosis of Field Air Defense Gun [J].Expert System with Application, 2011, 38:6007-6013. [4] 陈仁祥,汤宝平,吕忠亮.基于相关系数的EEMD转子振动信号降噪方法[J].振动、测试与诊断,2012,32(4):542-546. [5] 李兆飞,柴毅,李华峰.多重分形的振动信号故障特征提取方法[J].数据采集与处理,2013,28(1):237-243. [6] 李兵,张培林,任国全,等.形态学广义分形维数在发动机故障诊断中的应用[J].振动与冲击,2011,30(10):208-211. [7] Wu Z H,Huang N E. Ensemble empirical mode decomposition:a noise assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):7-12. [8] 杨明伦,邵华.基于EEMD和IMF能量分布的刀具破损识别[J].组合机床与自动化加工技术,2013(4):54-58. [9] 邓艾东,赵力,包永强.基于模糊熵的转子碰摩声发射信号的识别[J].机械工程学报,2010,46(3):71-75.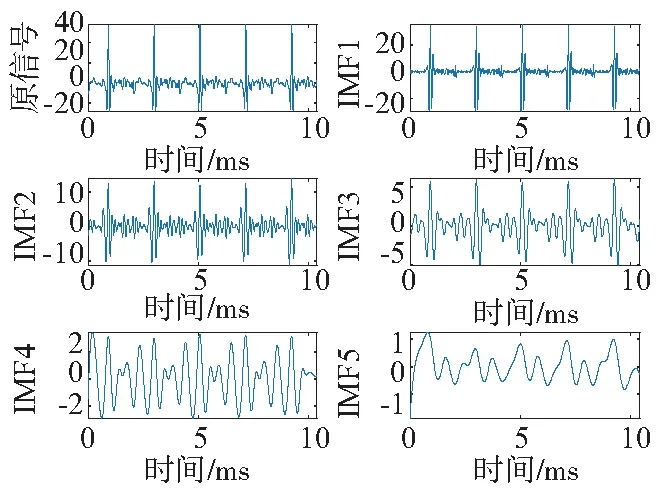
2.2 计算相关系数:

3 分形模糊熵特征值的提取方法

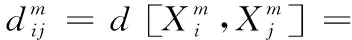
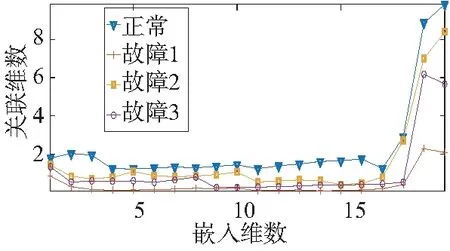
4 应用

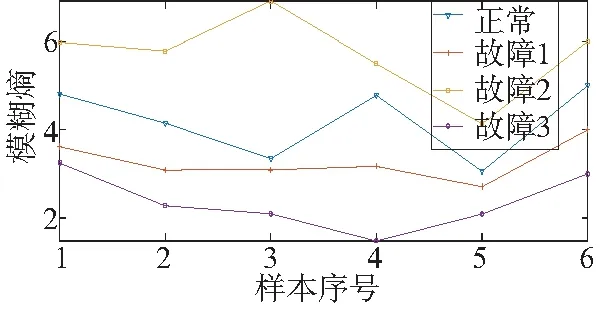

5 结论
——内燃机4.0 Highest Efficiency and Ultra Low Emission–Internal Combustion Engine 4.0

