一个广义Camassa-Holm方程的行波解*
涂郗,丘梅清,陆小钏,赖承栋,吴艾霞
(佛山科学技术学院数学与大数据学院,广东佛山528000)
随着近代物理学和数学的发展,早在1834年由英国科学家Russell发现的孤立波现象近20多年引起了人们的极大关注,人们对这一现象的研究兴趣与日俱增。这是因为一方面孤立子具有粒子和波的许多性能,在自然界中有一定的普遍性,利用孤立子理论也成功解释了许多物理上长期用经典理论未能解答的现象;另一方面,随着孤立子问题的深入探究,孤立子的数学理论也应运而生,并已初步形成比较完善的理论体系。
孤立子理论自1965年由Zabusky和Kruskal对孤立子(soltion,简称孤子)命名后得到了迅速的发展。究其原因是孤波现象无处不在,从天上涡旋星系的密度波、线、超流氦-3、超导Josephson结、磁学以及基本的粒子等等,都与我们上文提到的孤子有关。随着社会的发展,描述孤立波现象的方程不只有KdV方程,还有Burgers方程,Sine-Gordon方程,KP方程,Camassa-Holm(CH)方程等等。
1993年,美国阿尔莫斯国家实验室的科学家Camassa和 Holm[1]在研究浅水波运动规律时用Hamiltonian方法得到一个浅水波模型:
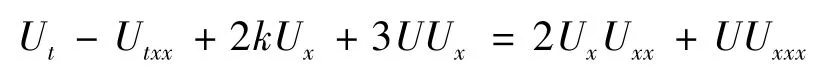
其中U是x方向上流体速度(或水的自由表面的高度),k是与临界浅水波波速相关的一个参数,下标表示偏导数。
CH方程是完全可积系统,具有哈密顿结构和无穷多守恒律[1-3],是一类非常奇特且重要的孤立波方程,且是一个小振幅的浅水波模型,当k=0是孤立子具有尖峰性质,当k≠0时孤立子无尖峰性质[1]。CH方程是第一个被发现能同时描述波裂现象和孤立子现象的浅水波方程 ,并且可以作为Euler方程自由边界问题的近似模拟。正是因为CH方程具有这些特性,许多数学家和物理学家对此产生极大的兴趣,它的数学研究也已取得大量的成果,如适定性[4-8],行波解[9-10]等。关于 CH方程的推广也得到了一些结果[11-15]。
本文要研究的方程恰是CH方程的推广,是一类特殊的广义的Camassa-Holm方程,也是完全可积的浅水波方程[16],即

其中U为流速。类似于CH方程,这个方程完全可积且可以很好地描述波裂现象和孤立子现象,且存在扭结解(波本身及其关于空间变量的一阶导数有界但二阶导数却在有限时间内产生奇性)[14-15]。Rehman,Gambino和 Roy Choudhury研究了该方程的行波解[17]。
在数学物理领域内,完全可积系统和浅水波模型的研究一直是热点,许多物理数学家对此保持极高的关注。从数学的角度来看,可积系统具有无穷多个守恒律。而守恒律是物理学中用于描述现实世界的基本定律,因此从数学理论推导出来的可积系统必定与现实世界存在着某种联系。我们对这些新型的可积系统进行深入的研究,这有助于人们更清楚地理解和认识客观世界。从物理学和工程学的角度看,靠近陆地的水波都可以近似的看成是浅水波。浅水波理论的研究,对实际应用是非常有帮助的。例如,海洋中最重要的一种现象:海啸。此外孤立子的轨道稳定性是数学家和物理学家最关注的问题,也值得我们深入研究,故本项目的研究在数学理论和实际应用中都有重要的意义。
对于本文要研究的特殊的广义的Camassa-Holm方程,我们用直接积分的方法计算出这个方程的所有初等积分形式,并分别讨论了c1≠0,且c2≠0与c1=c2=0两种情况下方程的积分形式,其中在计算当c1≠0,且c2≠0的其中一种Δ<0的情况时,采用了天珩公式来计算方程的积分形式。
方程(1)等价于下述方程

令 ξ=x-ct,则U(t,x)=V(ξ)。方程(2)可化为:

对ξ进行二次积分,并化简得

1 一般情况下行波解的积分表达式

(a)当Δ>0时,方程(4)有实数解:

即方程(3)有实数解:

令Vξ=0,该方程无解,故无积分表达式。
(b)当Δ=0时,方程(4)有2个实数解。
(I)方程(4)的第 1个实数根为X1=,即方程(3)有实数解

这是一个一元三次方程。令

由卡尔丹公式可得:
① 当Δ1>0时,方程(5)有解:
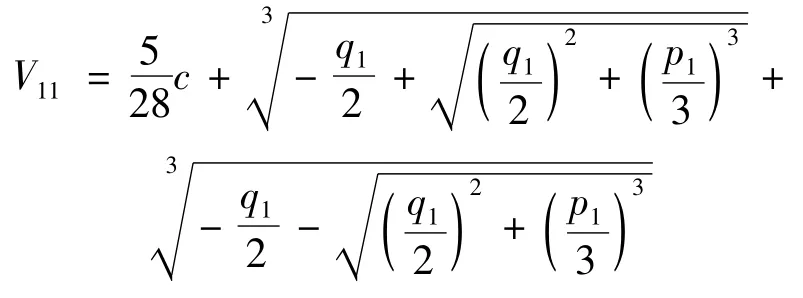
则其行波解的积分形式为
(i)当V11>0时,

(ii)当V11<0时,

②当Δ1=0时,方程(5)有2个实数根:第1个实数根为
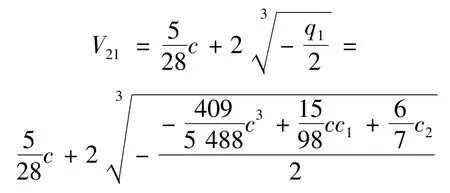
则其行波解的积分形式为
(iii)当V21>0时,
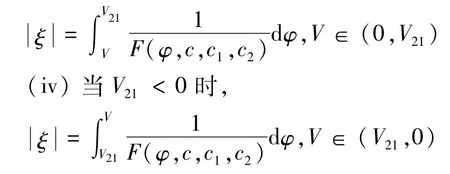
第2个实数根为

则其行波解的积分形式为

③当Δ1<0时,方程(5)有3个实数根:第1个实数根为

则其行波解的积分形式为
(vii)当V31>0时,

第2个实数根为

则其行波解的积分形式为
(ix)当V32>0时,

第3个实数根为

则其行波解的积分形式为
(xi)当V33>0时,

(II)方程(3)第二个实数根为
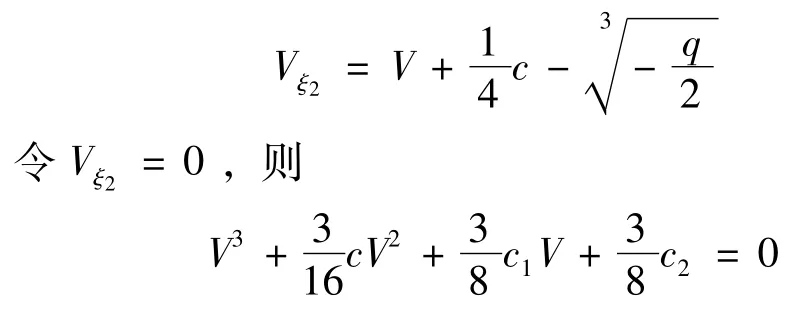
这也是一个一元三次方程,同理情况(I),我们可以得到在此情形下的积分形式。
(c)当Δ<0时,方程(5)有3个解。
(III)方程(3)的第1个实数根为:

令Vξ1=0,我们发现,满足以下方程


这是一个一元九次方程,由天珩公式可知,当时,该方程(6)有一实数根为

即方程Vξ1=0存在一解:

则其行波解的积分形式为

(IV)方程(3)的第2个实数根为

令Vξ2=0,我们可以得到满足一个一元九次方程,同样由天珩公式可知该方程的实数根,故同理可得到积分表达式。
(V)方程(3)第3个实数根为
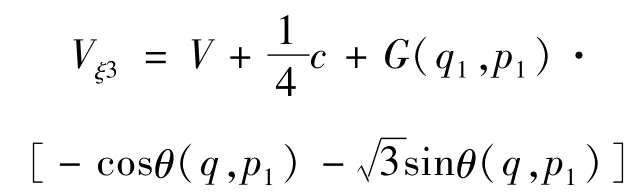
这种情况与情况(III)和情况(IV)相似,这里就不一一阐述。
2 特殊情况下行波解的积分表达式
当c1=c2=0时,

(a)当Δ=c(16V+3c)<0时,该一元三次方程只有1个实数根:
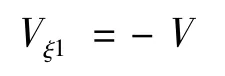
令Vξ1=0,则V=0为非极限零点,故无积分表达式。
(b)当Δ=c(16V+3c)=0时,该一元三次方程有2个实数根。
第1个实数根为

第2个实数根为

令Vξ2=0则V=为非极限零点,故无积分表达式。
(c)当Δ=c(16V+3c)>0时,该一元三次方程有3个实数根。
第1个实数根为

第2个实数根为

第3个实数根为
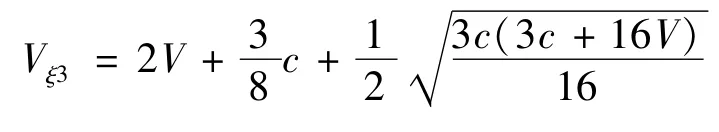
① 令Vξ2=0,得
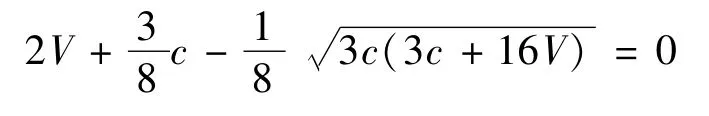
该方程等价于
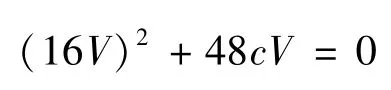
可得V=0,V=-,其中V1为极限零点,V2为非极限零点。其方程行波解的根的积分表达式为
(i)当c>0时,

(ii)当c<0时,

可得V1=0,V2=-,其中V1为极限零点,V2为非极限零点。其方程行波解的根的积分表达式为
(iii)当c>0时,

[1]CAMASSA R,HOLM D D.An integrable shallow water equation with peaked solitons[J].Phys Rev Lett,1993,71(11):1661-1664.
[2]CONSTANTIN A.The Hamiltonian structure of the Camassa-Holm equation[J].Exposition Math,1997,15(1):53-85.
[3]FUCHSSTEINER B,FOKASA S.Symplectic structures,their Bäcklund transformations and hereditary symmetries[J].Physica D Nonlinear Phenomena,1981,4(1):47-66.
[4]CONSTANTIN A.Existence of permanent and breaking waves for a shallow water equation:a geometric approach[J].Ann Inst Fourier,2000,50(2):321-362.
[5]CONSTANTIN A,ESCHER J.Global existence and blow-up for a shallow water equation[J].Annali Della Scuola Normale Superiore Di Pisa Classe Di Scienze,1998,26(2):303-328.
[6]CONSTANTIN A,ESCHER J.Well-posedness,global existence,and blowup phenomena for a periodic quasilinear hyperbolic equation[J].Comm Pure Appl Math,2015,51(5):475-504.
[7]DANCHIN R.A note on well-posedness for Camassa-Holm equation[J].J Differential Equations,2003,192(2):429-444.
[8]DANCHIN R.A few remarks on the Camassa-Holm equation[J].Differential Integral Equations,2001,14(8):953-988.
[9]赵小山,李震波.Camassa-Holm方程丰富的行波解[J].天津职业技术师范大学学报,2011,21(1):65-66.ZHAO X S,LIZ B.Abundant traveling wave solutions of Camassa-Holm equations[J].Journal of Tianjing University of Technology and Education,2011,21(1):65-66.
[10]田立新,许刚,刘曾荣.Camassa-Holm方程凹凸尖峰及光滑孤立子解[J].应用数学和力学,2002,23(5):60-69.TIAN L X,XU G,LIU C R.The concave or convex peaked and smooth soliton solutions of Camassa-Holm equation[J].Applied Mathematics and Mechanics,2002,23(5):60-69.
[11]张双虎,冯兆永,杨凯波.修正Camassa-Holm方程的Cauchy问题[J].中山大学学报(自然科学版),2014,53(4):8-12.ZHANG S H,FENG Z Y,YANG K B.The Cauchy problem for the modified Camassa-Holm equations[J].Acta Scientiarum Naturalium Universitatis Sunyatseni,2014,53(4):8-12.
[12]胡巧怡,金济,林利云,等.周期弱耗散的带旋度Camassa-Holm系统强解的整体存在性[J].中山大学学报(自然科学版),2012,51(3):35-38.HU Q Y,JIN J,LIN L Y,et al.Global existence for a weakly dissipative periodic Camassa-Holm system with vorticity[J].Acta Scientiarum Naturalium Universitatis Sunyatseni,2012,51(3):35-38.
[13]TU X,YIN Z.The Cauchy problem for a family of generalized Camassa-Holm equations[J].Appl Anal,2016,95(6):1184-1213
[14]TU X,YIN Z.Local well-posedness and blow-up phenomena for a generalized Camassa-holm equation with peakon solutions[J].Discrete Contin Dyn Syst A,2016,36(5):2781-2801.
[15]TU X,YIN Z.Blow-up phenomena and local well-posedness for a generalized Camassa-Holm equation in the critical Besov space[J].Nonlinear Anal,2015,128:1-19.
[16]SILVA PL D,FREIRE I L.Strict self-adjointness and certain shallow water models[J].2014,https://arxiv.org/abs/1312.3992.
[17]REHMAN T, GAMBINO G, CHOUDHURY S R.Smooth and non-smooth traveling wave solutions of some generalized Camassa-Holm equations[J].Commun Nonlinear Sci Numer Simul,2014,19(6):1746-1769.
[18]《数学手册》编写组.数学手册[M].北京:高等教育出版社,1979.

