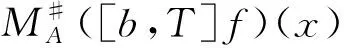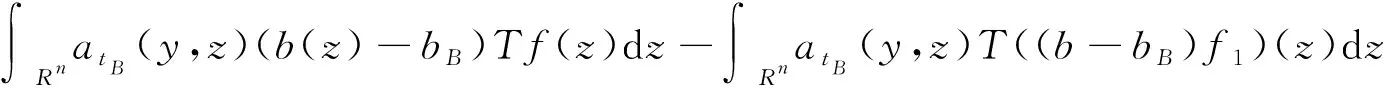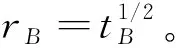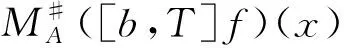带非光滑核的奇异积分算子交换子的加权有界性估计
吴翠兰, 王云杰, 束立生
(1.江苏师范大学 数学与统计学院,江苏 徐州 221116;2.江苏师范大学 科文学院,江苏 徐州 221116;3.安徽师范大学 数学与统计学院,安徽 芜湖 241003)
1 引言及主要结果
对1 其中f为具有紧支集的连续函数,且x∉suppf。若K(x,y)满足 及 称K(x,y)满足Hörmander条件。 核函数K(x,y)满足Hörmander条件的奇异积分算子和交换子的有界性得到了广泛的研究,并取得了许多结果,见文[1]等。1999年,Duong等[2]在核函数满足更弱的条件下证明了具有非光滑核的奇异积分算子T在Lp(1 Duong和Mcintosh在文[2]中引入了具有非光滑核的奇异积分算子,定义如下: 定义1.1设at(x,y)(t>0)是定义在属于Rn×Rn上的可测函数,At是以at(x,y)为核函数的算子。如果对任意的f∈Lp(Rn),1p<, (1) 且对于(x,y)∈Rn×Rn,t>0,有 |at(x,y)|ht(x,y) (2) 其中g是正的有界递减函数且满足 (3) 这里ε>0,称算子族{At:t>0}为恒等逼近。 若K满足下列条件: (i)存在一恒等逼近{Bt:t>0},使得TBt具有相关的核函数kt(x,y),且存在C1,C2>0,使得对所有的y∈Rn,有 (ii)存在一恒等逼近{At:t>0},使得AtT具有相关的核函数Kt(x,y)满足 |K(x,y)-Kt(x,y)| 在文[2]中,Duong和Mcintosh证明了如果选取合适的恒等逼近,条件(i)和(ii)比添加给Calderón-Zygumd算子一些常见的条件(如Hömander条件)弱。同时,作者还证明了如果算子T满足(i),则算子T不仅是弱(1)型的,而且还是强(p,p)(1p2)的。此外,若算子T满足(i)和(ii),则算子T是强(p,p)(1 1985年,Bloom在文[7]中得到经典的奇异积分算子的交换子定理: 定理A设1 2008年,Hu和Gu在文[8]中研究了Calderón-Zygumd奇异积分算子T的加权Lipschtiz估计。 定理B设T是Calderón-Zygumd奇异积分算子,μ∈A1,1/q=1/p-β/n,0<β<1,1 2012年,陈晓莉等在[9]中研究了具有非光滑核的奇异积分算子交换子的加权BMO估计,结论如下: 定理C设算子T是具有非光滑核的奇异积分算子,μ,v∈Ap,1 ||[b,T]f||Lp(ν)C||b||*,ω||f||Lp(μ)。 受以上研究的启发,本文将文献[2]中结果推广到加权情形,讨论具有非光滑核的奇异积分算子交换子的加权估计。我们的结论是: 定理1.1设算子T是具有非光滑核的奇异积分算子,b∈Lipβ,ν,v∈A1,1/q=1/p-β/n,其中0<β<1,1 定义2.1极大函数Mf(x),Sharp极大函数M#f(x)分别定义如下: 此外,对δ>0,定义 定义2.2(1)设1 如果存在常数C,使得 Mω(x)Cω(x)a.e.x∈Rn, 则称ω∈A1. (2)如果 其中1/p+1/p'=1,则称ω∈A(p,q)(1 定义2.3设b为Rn上局部可积函数,1p,v∈A(Rn),如果 设f∈Lp(Rn)(1 Martell在文[11]中证明了下面的引理: 引理2.1[11]若f∈Lp(Rn)(1 引理2.2[10](1)若v∈A1,b∈Lipβ,v,x∈B。则 |b2jB-bB|Cjv(x)||b||Lipβ,νv(2jB)β/n。 (2)若v∈A1,b∈Lipβ,ν,则 引理2.3若ν∈A1,则对r>1及任何球B,有 由Ap权的定义及性质即可证明引理2.3. 引理2.4[3,11]设T是具有非光滑核的奇异积分算子,v∈A1,则 ||Tf||Lp(v)C||f||Lp(v)。 引理2.5[10]若0<β<1,1r<,ν∈A(p,q),记 ||Mβ,ν,r(f)||Lq(ν)C||f||Lp(ν)。 引理2.6设{At:t>0}是恒等逼近,0<β<1,b∈Lipβ,ν,ν∈A1,1 证明设f∈Lp(v)(p>1),对任意的x∈Rn,B是包含x的任意球,则由定义1.1 (4) 首先估计I1。由(2)式及g是正的有界递减函数,对y∈B,z∈2B,有 htB(y,z) 因此,由引理2.2,引理2.3及Hölder不等式可得 (5) 下面我们估计I2。当y∈B,z∈2j+1B2jB时,有|y-z|≥2j-1rB,且 htB(y,z) 从而 (6) 类似于I1的估计方法,可得 (7) 由(6)-(7)得 由(3)式得 从而 I2C||b||Lipβ,νv(x)Mβ,v,r(f)(x)。 (8) 根据I1和I2的估计 为证明定理1.1,先证明下列引理. 引理3.1设算子T是具有非光滑核的奇异积分算子,b∈Lipβ,v,v∈A1,1/q=1/p-β/n,1r 证明设f∈Lp(v)(p>1),固定x∈Rn及x∈B,令 f(x)=f(x)χ2B(x)+f(x)χ(2B)c(x)=f1(x)+f2(x)。 由于 =AtB((b-bB)Tf)(y)-AtBT((b-bB)f1)(y)-AtBT((b-bB)f2)(y)。 因此 =I+II+III+IV+V。 对于I,取1 对于II,由Hölder不等式及算子T的Lr有界性,有 至于III,由引理2.6得 对于IV,类似于II的估计,易得 综合I-V的估计,可得 定理1.1的证明由v∈A1知v1-q∈Aq,又1 ||[b,T]f||Lq(v1-q)||M([b,T]f)||Lq(v1-q) 定理1.1证毕。 参考文献: [2] DUONG X T,MCINTOSH A.Singular integral operators with non-smooth kernels on irregular domains [J].Rev Math Iberoamericana,1999,15(2):233-265. [3] DENG D G,YAN L X.Commutators of singular integral operators with non-smooth kernels [J].Acta Math Sci,2005,25(1):137-144. [4] LIU Lanzhe.Boundedness properties for multilinear singular integral operators with non-smooth kernels [J].Acta Math Scientia,2010,30A(1):167-178. [5] LIAN J L,WU H X.Lipschitz estimates for the commutators of multilinear singular integrals with non-smooth kernels [J].Advances in mathematics,2013,42(6):748-762. [6] XU J H.Multilinear commutators of singular integral operators with non-smooth kernels [J].Taiwanese Journal of Mathematics,2007,11(2):483-496. [7] BLOOM S.A commutator theorem and weighted BMO [J].Trans Amer Math Soc,1985(292):103-122. [8] HU B,GU J J.Necessary and sufficient conditions for boundedness of some commutators weighted Lipschitz functons [J].J Math Anal Appl,2008(340):598-605. [9] CHEN X L,CHEN J H.Weighted BMO estimates for commutators of singular integrals with non-smooth kernels [J].Acta Math Sinica,2012,55(5):861-868. [10] GARCIA-CUERVA J,RUBIO DEFRANCIA J L.Weighted norm inequalities and related topics [M].New York:North-Holland Amsterdam,1985. [11] MARTELL J M.Shap maximal functions associated with approximations of the identity in spaces of homogeneous type and applications [J].Studia Math,2004(161):113-145.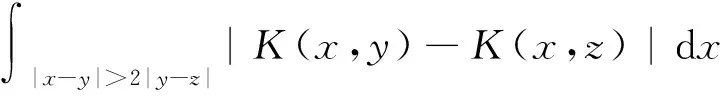




2 预备知识


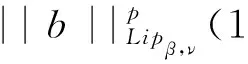
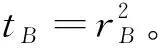
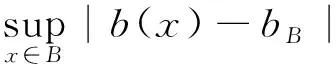


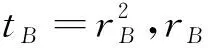



3 定理的证明