带LCL滤波三相并网逆变器准比例谐振控制

(广西大学电气工程学院，广西 南宁 530004)

1 引言

依托全球能源使用增加的背景，可再生能源持续增长，并将逐渐成为深受欢迎的主流能源。作为新能源发电单元与电网之间必不可少的能量转换接口，并网逆变器对分布式发电系统的安全、稳定和高质量运行具有十分重要的作用[1-2]。因此研究高效的并网逆变器控制策略具有重要的现实意义。

为了抑制逆变器的并网电流谐波，必须在其近网侧增加滤波器。在并网逆变系统中，主要采用两种滤波器型单L电感结构和LCL结构两种滤波器。L型滤波器为一阶环节，控制性能较好，系统易于稳定，并且结构简单，使并网系统中经常采用的滤波方式。但单电感滤波器对电流纹波的衰减与频率成正比，对纹波的抑制能力较差，因此滤波电感大。而LCL滤波器成本低、体积小、动态性能好，且具有更好的谐波抑制能力[3]。因此，在开关频率较低的大功率光伏并网发电系统中，通常使用LCL滤波器。然而，LCL滤波器是一个典型的三阶环节，其低阻尼性会使其频率响应在谐振频率处存在谐振尖峰，容易造成并网逆变器振荡甚至不稳定。目前有以下两种抑制谐振尖峰的方法使用较为广泛：一种是无源阻尼法，即在LCL滤波器中加入实际的阻尼电阻，另一种方法是有源阻尼法，由控制算法来等效出一个与实际电阻作用相同的控制策略[4-6]。

由于PI 控制器只能对直流信号实现无静差控制，在三相情况下，它的跟踪性能会有偏差，功率因数较低，很难保持系统的稳定[7]。虽然三相abc坐标系可以经过PARK变换转换为dq两相旋转坐标系，再由PI控制对并网电流进行调节。但是LCL滤波器为三阶滤波，d/q坐标系下会出现电压、电流控制的三个耦合项，这给闭环系统的解耦带来了十分大的困难，增加了控制策略的复杂程度。而准PR控制器则很好地克服了PI控制器存在的问题。α/β坐标系下两个坐标轴电流控制量没有耦合，相互独立，无需进行解耦计算，可以使闭环控制系统控制策略得以简化[8-9]。

本文采用LCL型并网逆变器，引入电容电流反馈，增加系统阻尼抑制谐振尖峰。在α/β标系下采用准PR控制器实现无静差跟踪。最后，在指令电流发生变化时，对d/q坐标系的PI控制和本文提出的控制策略的仿真进行对比分析，验证了控制策略的优越性。

2 三相LCL逆变器建模

2.1 LCL型逆变器结构图与数学模型

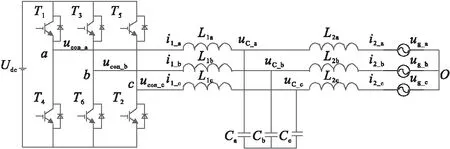
图1 LCL滤波三相并网逆变器拓扑结构

三相静止坐标系下的数学模型

(1)

(2)

(3)

其中，分ucon_a(t)、ucon_b(t)、ucon_c(t)别代表LCL型逆变器侧电压；ucon_a(t)、ucon_b(t)、ucon_c(t)分别代表三相电容两端电压；ug_a(t)、ug_b(t)、ug_c(t)分别代表三相电网电压；i1_a(t)、i1_b(t)、i1_c(t)分别代表逆变器侧三相电感电流；i2_a(t)、i2_b(t)、i2_c(t)分别代表电网侧三相电感电流；P=d/dt为微分算子。

2.2 LCL滤波器幅频特性以及有源阻尼

为更好分析比较L型滤波器和LCL型滤波器滤波效果之间的差异，假设L型滤波器电感值为L，而LCL型滤波器逆变器与网侧的电感值分别为L1和L2，即L=L1+L2；二者传递函数分别为：

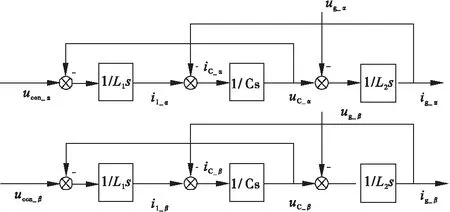
图2 α/β两相静止坐标系下的数学模型

图3 d/q两相旋转坐标系下的数学模型

(4)

(5)

分别绘制波德图：

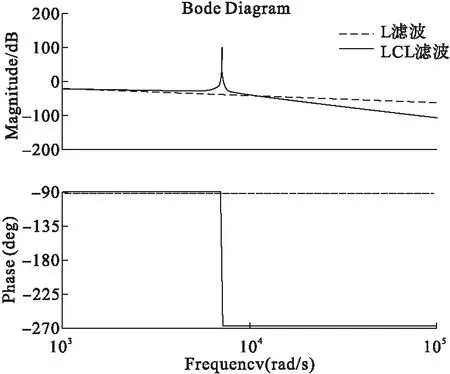
图4 L型和LCL型逆变器波德图

由图4可知，L型和LCL型滤波器的衰减率在低于转折频率的情况下均为，两者的衰减情况是相同的；在高于转折频率的情况下，L型滤波器依然以的速率衰减，而LCL型滤波器的衰减率则增加至-40dB/dec，其对于开关频率及以上高次谐波的衰减效果更好。所以在确保电流高次谐波获得相同衰减效果的情况下，采用 LCL型滤波器时其总的电感电抗值要远低于单电感 L型滤波器，可以更好地滤除开关频率及以上的电流高次谐波分量。但由于谐振峰值的存在，会使并网逆变器输出电流振荡甚至导致系统不稳定，为保证并网逆变器稳定，需要对谐振尖峰进行阻尼。相对于添加阻尼电阻的无源阻尼方法，引入电容过电流反馈的有源阻尼方法更加灵活，也可以避免阻尼电阻损耗。

图5和图6分别为没有引入电容电流反馈和引入电容电流反馈的结构框图。

图5 无电容电流反馈框图

图6 有电容电流反馈框图

忽略电网点扰动时，可有图5、6分别推导出其开环传递函数分别为：

(6)

(7)

为了定性分析二者关系，忽略电流调节器作用。根据上述传递函数绘制零极点图和波特图。由零极点图分析可知，电容电流反馈的引入会使原本在虚轴上的一对极点向左半平面移动，使系统趋于稳定。而由波特图分析可知，引入带反馈系数的电容电流反馈后，系统阻尼加大，使谐振峰值降低，且随着反馈系数的增大，其谐振抑制效果更好，但是比例系数过大，系统的快速性会降低，调节时间会加大，同时系统的相位裕度也会明显减小。

假设引入电容电流反馈后系统阻尼系数为ξ=0.707和谐振频率ω，则有：

(8)

此时，设KPWM=100，则可以计算出电容电流反馈系数:

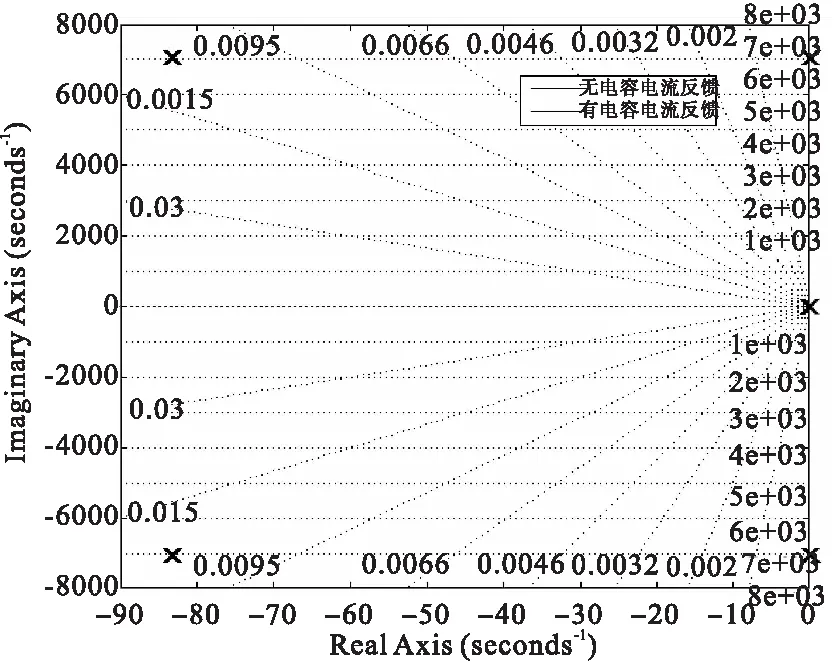
图7 有无电容电流反馈零极点图

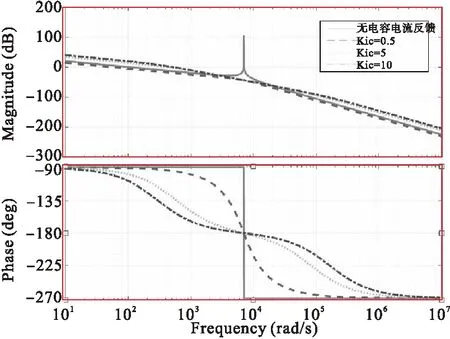
图8 有无电容电流反馈零极点图

3 控制器的选取

3.1 PI控制器与准PR控制器对比分析

并网电流反馈电流调节器PI控制器与准PR控制器传递函数分别为：

(9)

(10)

其中，ω0是基波角频率。

对比两种控制器的波德图可知：QPR控制器在某一谐振频率处有一个非常大的增益，在其他各处频率点的增益都非常小，同时又把带宽增加了，这会使得有高增益的范围变大，电流控制器抗扰动能力升髙。另外，QPR控制器对交流量的跟踪可以做到无静差。

3.2 准PR控制器参数分析

由准PR控制的传递函数可以看出，其有3个参数Kp、Kr、ωc。因此需要分析各参数对控制系统的影响，以此来确定参数的选取。 参数变化时QPR控制器传递函数波特图见图10。

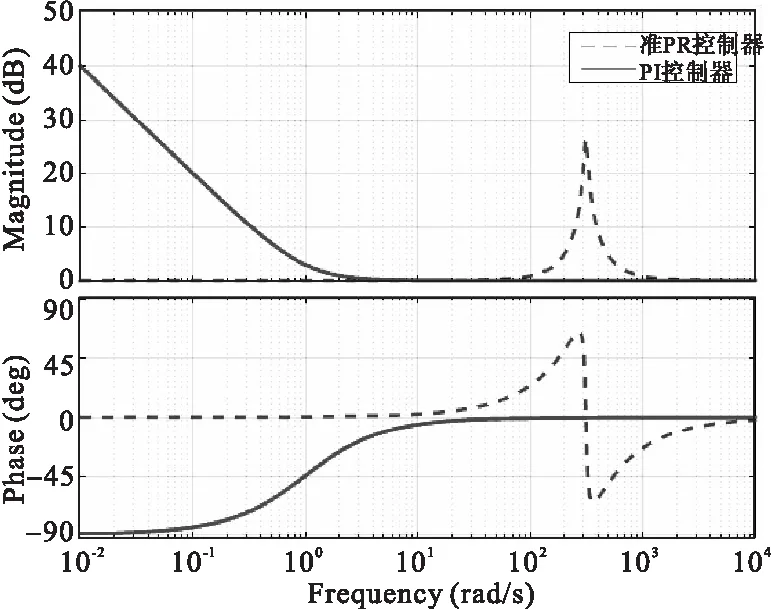
图9 PI、QPR控制器性能对比

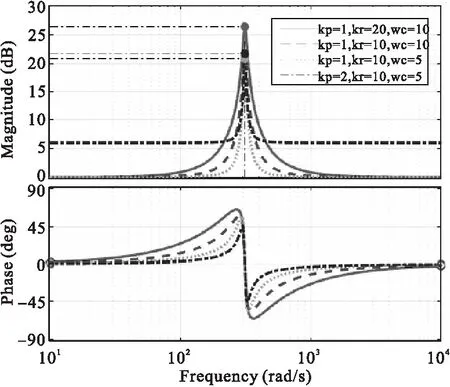
图10 QPR控制器参数分析

由图10可以看出，三个参数相互影响作用很小。参数Kr对于控制器性能影响主要体现在基频部分，而低频和高频部分几乎没有影响。基频处幅值增益随Kr的增大而增大，从而减小系统基频处的稳态误差；在不影响系统动态响应的前提下，Kp越小低频与高频处的幅值增益越小；ωc的增大有利于提高系统带宽，增强系统鲁棒性。

4 仿真结果与分析

为验证控制策略的有效性，本文在在MATLAB/simulink中分别搭建PI控制和准PR控制仿真模型，并对结果进行分析。仿真模型主要参数如1表所示。

由仿真可知，采用 PI 控制时并网电流的正弦度较好，实现了与相电压同频同向，但是有明显的纹波，其并网电流THD值为3.04%。而QPR控制电流纹波较小，并网电流THD值为2.39%。由图可知，采用准PR控制器时，并网电流误差较小，仅为2%。

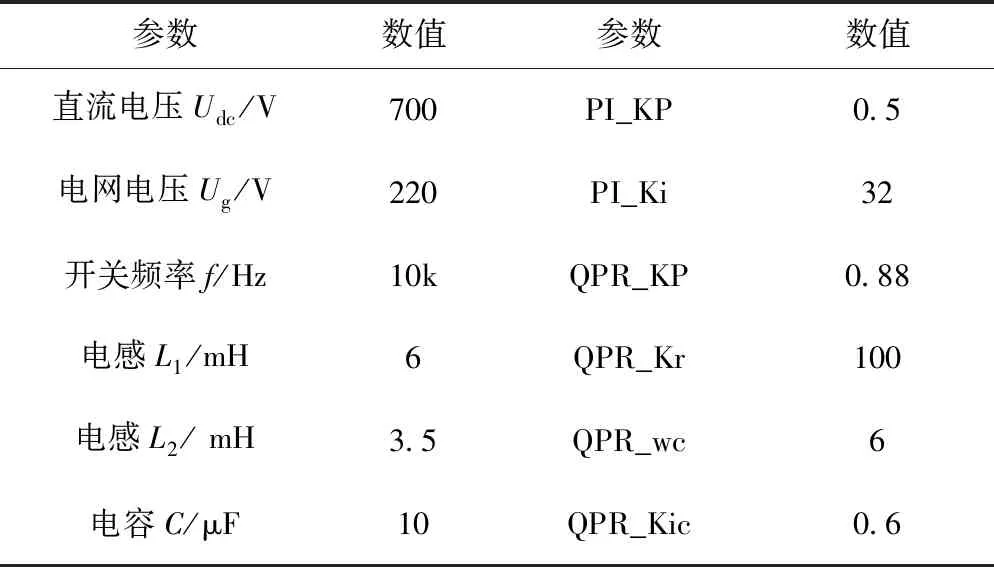
表1 并网逆变器主要参数

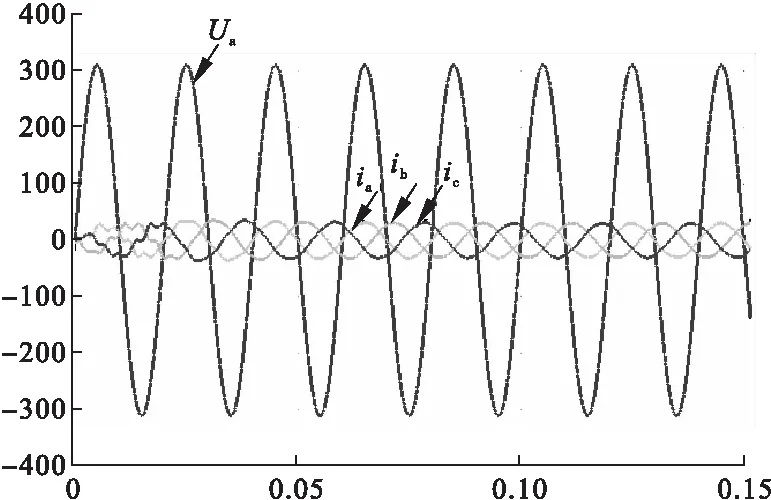
图11 PI控制A相电压与三相并网电流波形

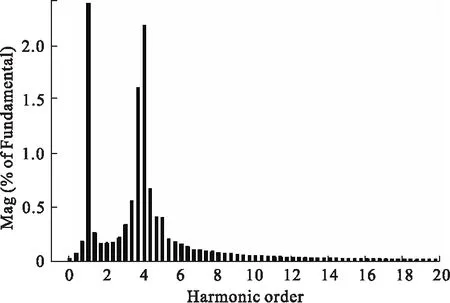
图12 PI控制并网电流THD

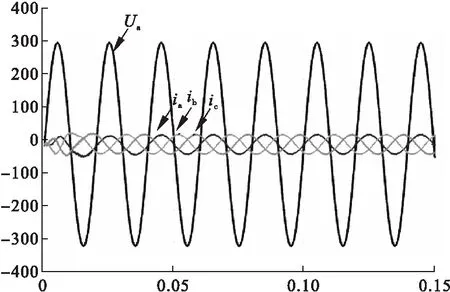
图13 QPR控制A相电压与三相并网电流波形

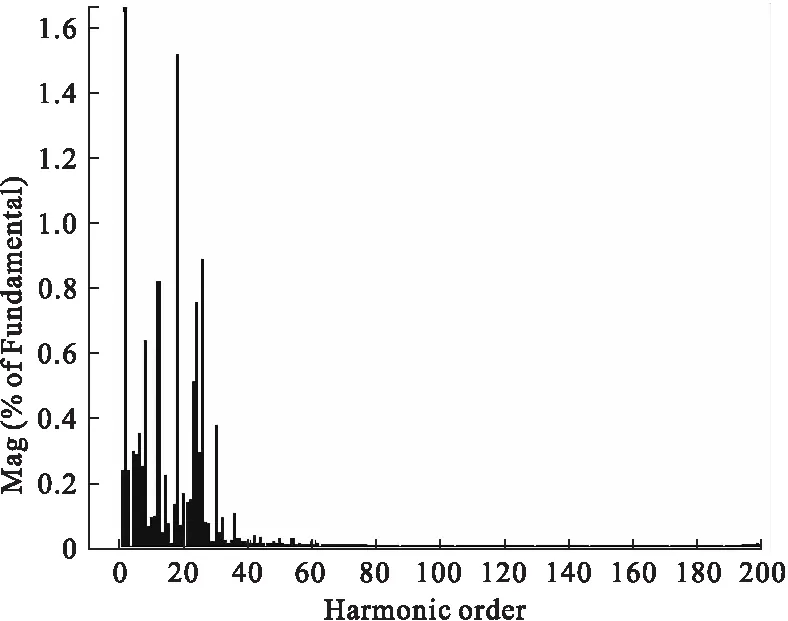
图14 QPR控制并网电流THD

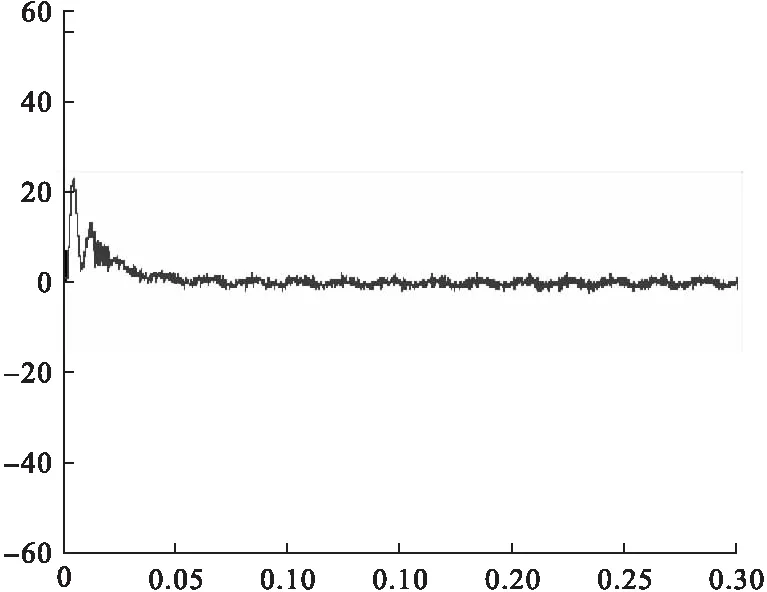
图15 准PR控制并网电流误差

在t=0.2s时，将指令电流有30A突变为15A。得出分别采用两种控制器的并网电流波形。

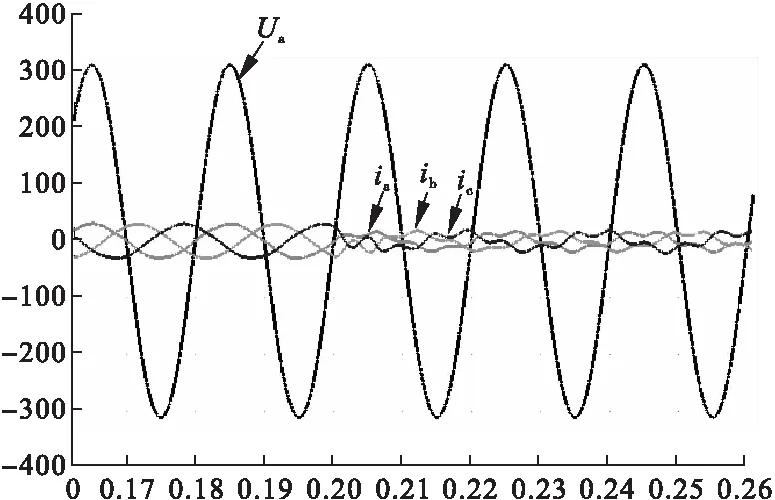
图16 指令电流突变PI控制

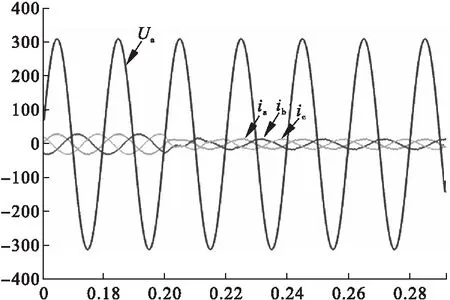
图17 指令电流突变QPR控制

由图16、17可知，指令电流突变时，采用PI控制时，并网电流发生畸变不能很好跟踪指令电流；而采用QPR控制时，不仅动态响应较快，而且并网电流依然可以很好跟踪指令电流。

5 总结

本文对PI 控制和准PR控制进行对比，得出引入电容电流反馈有源阻尼的准PR控制策略能很好的抑制高频谐波，且稳态电流具有更低的谐波畸变率和更好的跟踪效果，稳态电流波形质量明显提高。且在电流指令突变的情况下，准PR控制依然能保持良好的稳定性和跟踪性能。